Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:39:34.575Z Has data issue: false hasContentIssue false
  • English
  • Français

BINARY KRIPKE SEMANTICS FOR A STRONG LOGIC FOR NAIVE TRUTH

Part of: General logic

Published online by Cambridge University Press:  21 December 2020

BEN MIDDLETON
BEN MIDDLETON*
Affiliation:
DEPARTMENT OF PHILOSOPHY UNIVERSITY OF NOTRE DAMENOTRE DAME, IN46556, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

I show that the logic 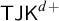$\textsf {TJK}^{d+}$ , one of the strongest logics currently known to support the naive theory of truth, is obtained from the Kripke semantics for constant domain intuitionistic logic by (i) dropping the requirement that the accessibility relation is reflexive and (ii) only allowing reflexive worlds to serve as counterexamples to logical consequence. In addition, I provide a simplified natural deduction system for $\textsf {TJK}^{d+}$ , in which a restricted form of conditional proof is used to establish conditionals.

Keywords

Naive truthTJKcompletenessdisjunction propertyexistence propertysubintuitionisticbinary Kripke semanticsnatural deductionconditional proof

MSC classification

Primary: 03B60: Other nonclassical logic
Type
Research Article
Information
The Review of Symbolic Logic , Volume 15 , Issue 3 , September 2022 , pp. 668 - 692
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Bacon, A. (2013a). A new conditional for naive truth theory. Notre Dame Journal of Formal Logic, 54(1), 87–104.CrossRefGoogle Scholar
Bacon, A., (2013b). Curry’s paradox and $\omega$ -inconsistency. Studia Logica, 101, 1–9.CrossRefGoogle Scholar
Beall, J. (2009). Spandrels of Truth. New York: Oxford University Press.CrossRefGoogle Scholar
Brady, R. (1984). Natural deduction systems for some quantified relevant logics. Logique Et Analyse, 27(8), 355–377.Google Scholar
Brady, R., (2006). Universal Logic. Stanford, CA: Center for the Study of Language and Information.Google Scholar
Field, H., Lederman, H., & Øgaard, T. F. (2017). Prospects for a naive theory of classes. Notre Dame Journal of Formal Logic, 58(4), 461–506.CrossRefGoogle Scholar
Halbach, V. (2014). Axiomatic Theories of Truth. New York: Cambridge University Press.CrossRefGoogle Scholar
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72(19), 690–716.CrossRefGoogle Scholar
Middleton, B. (2020). A canonical model for constant domain basic first-order logic. Studia Logica, 108, 1307–1323.CrossRefGoogle Scholar
Poizat, B. (2000). A Course in Model Theory: An Introduction to Contemporary Mathematical Logic. New York: Springer.CrossRefGoogle Scholar
Priest, G. (2002). Paraconsistent Logic. In Gabbay, D. M. and Guenthner, F., editors. Handbook of Philosophical Logic (second edition), Vol. 6. Dordrecht: Kluwer Academic Publishers, pp. 287–393.CrossRefGoogle Scholar
Restall, G. (1994). Subintuitionistic logics. Notre Dame Journal of Formal Logic, 35(1), 116–129.CrossRefGoogle Scholar
Ruitenburg, W. (1998). Basic predicate calculus. Notre Dame Journal of Formal Logic, 39(1), 18–46.CrossRefGoogle Scholar
Visser, A. (1981). A propositional logic with explicit fixed points. Studia Logica, 40, 155–175.CrossRefGoogle Scholar