Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T22:11:01.692Z Has data issue: false hasContentIssue false
  • English
  • Français

AN ALGEBRAIC APPROACH TO INQUISITIVE AND 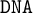$\mathtt {DNA}$-LOGICS

Part of: Distributive lattices Varieties Boolean algebras (Boolean rings) General logic

Published online by Cambridge University Press:  02 December 2021

NICK BEZHANISHVILI ,
GIANLUCA GRILLETTI Open the ORCID record for GIANLUCA GRILLETTI [Opens in a new window]  and
DAVIDE EMILIO QUADRELLARO
NICK BEZHANISHVILI
Affiliation:
INSTITUTE FOR LOGIC LANGUAGE AND COMPUTATION UNIVERSITY OF AMSTERDAM
GIANLUCA GRILLETTI
Affiliation:
MUNICH CENTRE FOR MATHEMATICAL PHILOSOPHY LUDWIG MAXIMILLIAN UNIVERSITY
DAVIDE EMILIO QUADRELLARO
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF HELSINKI
Get access Rights & Permissions [Opens in a new window]

Abstract

This article provides an algebraic study of the propositional system 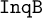$\mathtt {InqB}$ of inquisitive logic. We also investigate the wider class of 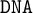$\mathtt {DNA}$-logics, which are negative variants of intermediate logics, and the corresponding algebraic structures, 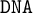$\mathtt {DNA}$-varieties. We prove that the lattice of 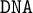$\mathtt {DNA}$-logics is dually isomorphic to the lattice of 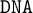$\mathtt {DNA}$-varieties. We characterise maximal and minimal intermediate logics with the same negative variant, and we prove a suitable version of Birkhoff’s classic variety theorems. We also introduce locally finite 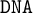$\mathtt {DNA}$-varieties and show that these varieties are axiomatised by the analogues of Jankov formulas. Finally, we prove that the lattice of extensions of 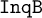$\mathtt {InqB}$ is dually isomorphic to the ordinal 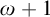$\omega +1$ and give an axiomatisation of these logics via Jankov 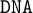$\mathtt {DNA}$-formulas. This shows that these extensions coincide with the so-called inquisitive hierarchy of [9].1

Keywords

inquisitive logicintermediate logicsnegative variantsHeyting algebrasalgebraic semantics

MSC classification

Primary: 03B55: Intermediate logics
Secondary: 03B60: Other nonclassical logic 06D20: Heyting algebras 08B15: Lattices of varieties
Type
Research Article
Information
The Review of Symbolic Logic , Volume 15 , Issue 4 , December 2022 , pp. 950 - 990
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This article is based on [41].

References

BIBLIOGRAPHY

Abramsky, S., & Väänänen, J. (2009). From IF to BI. Synthese, 167(2), 207–230.CrossRefGoogle Scholar
Bezhanishvili, G., & Bezhanishvili, N. (2009). An algebraic approach to cano nical formulas: intuitionistic case. Review of Symbolic Logic, 2(3), 517–549.CrossRefGoogle Scholar
Bezhanishvili, G., & Bezhanishvili, N. (2011). An algebraic approach to canonical formulas: modal case. Studia Logica, 99(1–3), 93–125.CrossRefGoogle Scholar
Bezhanishvili, N. (2006). Lattices of Intermediate and Cylindric Modal Logics. PhD Thesis, ILLC, University of Amsterdam.Google Scholar
Bezhanishvili, N., Grilletti, G., & Holliday, W. H. (2019). Algebraic and topological semantics for inquisitive logic via choice-free duality. In Iemhoff, R., Moortgat, M., & de Queiroz, R., editors. Logic, Language, Information, and Computation. Berlin, Heidelberg: Springer, pp. 35–52.CrossRefGoogle Scholar
Blackburn, P., de Rijke, M., & Venema, Y. (2002). Modal Logic. Cambridge: Cambridge University Press.Google Scholar
Burris, S. N., & Sankappanavar, H. (1981). A Course in Universal Algebra. New York: Springer.CrossRefGoogle Scholar
Chagrov, A., & Zakharyaschev, M. (1997). Modal Logic. Oxford: Clarendon Press.CrossRefGoogle Scholar
Ciardelli, I. (2009). Inquisitive Semantics and Intermediate Logics. MSc Thesis, University of Amsterdam.Google Scholar
Ciardelli, I. (2016). Dependency as question entailment. In Abramsky, S., Kontinen, J., Väänänen, J., & Vollmer, H., editors. Dependence Logic: Theory and Applications. Cham: Springer International Publishing, pp. 129–181.CrossRefGoogle Scholar
Ciardelli, I. (2016). Questions in Logic. PhD Thesis, University of Amsterdam.Google Scholar
Ciardelli, I., Groenendijk, J., & Roelofsen, F. (2011). Attention! Might in inquisitive semantics. In Cormany, E., Ito, S., and Lutz, D., editors. Proceedings of Semantics and Linguistic Theory (SALT) 19. eLanguage, pp. 91–108.Google Scholar
Ciardelli, I., Groenendijk, J., & Roelofsen, F. (2018). Inquisitive Semantics. Oxford: Oxford University Press.CrossRefGoogle Scholar
Ciardelli, I., & Roelofsen, F. (2011). Inquisitive logic. Journal of Philosophical Logic, 40(1), 55–94.CrossRefGoogle Scholar
Citkin, A. (2014). Characteristic formulas 50 years later (an algebraic account). arXiv:1407.5823 [math.LO].Google Scholar
Davey, B., & Priestley, H. (1990). Introduction to Lattices and Orders. Cambridge: Cambridge University Press.Google Scholar
de Jongh, D. (1968). Investigations on the Intuitionistic Propositional Calculus. PhD Thesis, University of Wisconsin.Google Scholar
Esakia, L. (2019). Heyting Algebras. Duality Theory. Bezhanishvili, G., & Holliday, W. H.. Trans. by A. Evseev. Berlin: Springer International Publishing.CrossRefGoogle Scholar
Fine, K. (1974). An ascending chain of S4 logics. Theoria, 40(2), 110–116.CrossRefGoogle Scholar
Font, J. M. (2016). Abstract Algebraic Logic. An Introductory Textbook. London: College Publication.Google Scholar
Frittella, S., Greco, G., Palmigiano, A., & Yang, F. (2016). A multi-type calculus for inquisitive logic. In Väänänen, J., Hirvonen, Å., and de Queiroz, R., editors. Logic, Language, Information, and Computation. Berlin, Heidelberg: Springer, pp. 21–233.CrossRefGoogle Scholar
Galatos, N., Jipsen, P., Kowalski, T., and Ono, H. (2007). Residuated Lattices: An Algebraic Glimpse at Substructural Logics. Amsterdam: Elsevier.Google Scholar
Ghilardi, S., & Santocanale, L. (2020). Free Heyting algebra endomorphisms: Ruitenburg’s theorem and beyond. Mathematical Structures in Computer Science, 30(6), 572–596.CrossRefGoogle Scholar
Grilletti, G., & Quadrellaro, D. E. (2020). Lattices of intermediate theories via Ruitenburg’s theorem. arXiv:2004.00989 [math.LO].Google Scholar
Groenendijk, J., & Stokhof, M. (1982). Semantic analysis of Wh-complements. Linguistics and Philosophy, 5(2), 175–233.CrossRefGoogle Scholar
Groenendijk, J., & Stokhof, M. (1984). Studies on the Semantics of Questions and the Pragmatics of Answers. Joint PhD Thesis, University of Amsterdam.Google Scholar
Groenendijk, J., & Roelofsen, F. (2009). Inquisitive semantics and pragmatics. In Larrazabal, J. M., & Zubeldia, L., editors. Meaning, Content, and Argument: Proceedings of the ILCLI International Workshop on Semantics, Pragmatics, and Rhetoric. San Sebastián: Universidad del País Vasco, Servicio Editorial, pp. 41–72.Google Scholar
Ilin, J. (2018). Filtration Revisited: Lattices of Stable Non-Classical Logics. PhD Thesis, University of Amsterdam.Google Scholar
Jankov, V. (1963). On the relation between deducibility in intuitionistic propositional calculus and finite implicative structures. Soviet Mathematics Doklady, 151, 1294–1294.Google Scholar
Jankov, V. (1968). The calculus of the weak “law of excluded middle”. Mathematics of the USSR-Izvestiya, 2(5), 997–1004.CrossRefGoogle Scholar
Jankov, V. (1968). The construction of a sequence of strongly independent superintuitionistic propositional calculi. Soviet Mathematics Doklady, 9, 806–807.Google Scholar
Jipsen, P., & Litak, T. (2022). An algebraic glimpse at bunched implications and separation logic. In Galatos, N., and Terui, K., editors. Hiroakira Ono on Substructural Logics. Cham: Springer International Publishing, pp. 185–242.CrossRefGoogle Scholar
Kreisel, G., & Putnam, H. (1958). Eine Unableitbarkeitsbeweismethode Für den Intuitionistischen Aussagenkalkül. Journal of Symbolic Logic, 23(2), 229–229.Google Scholar
Maksimova, L. L. (1986). On maximal intermediate logics with the disjunction property. Studia Logica, 45(1), 69–75.CrossRefGoogle Scholar
Maltsev, A. I. (1973). Algebraic systems. Translated from the Russian by B. D. Seckler and A. P. Doohovskoy. Berlin: Springer.Google Scholar
Medvedev, J. (1962). Finite problems. Soviet Mathematics Doklady, 3(1), 227–230.Google Scholar
Miglioli, P., Moscato, U., Ornaghi, M., Quazza, S., & Usberti, G. (1989). Some results on intermediate constructive logics. Notre Dame Journal of Formal Logic, 30(4), 543–562.CrossRefGoogle Scholar
Punčochář, V. (2016). A generalization of inquisitive semantics. Journal of Philosophical Logic, 45(4), 399–428.CrossRefGoogle Scholar
Punčochář, V. (2019). Substructural inquisitive logics. Review of Symbolic Logic, 12(2), 296–330.CrossRefGoogle Scholar
Punčochář, V. (2015). Weak negation in inquisitive semantics. Journal of Logic, Language, and Information, 24(3), 323–355.CrossRefGoogle Scholar
Quadrellaro, D. E. 2019. Lattices of $DNA$ -Logics and Algebraic Semantics of Inquisitive Logic. MSc Thesis, University of Amsterdam.Google Scholar
Roelofsen, F. (2013). Algebraic foundations for the semantic treatment of Inquisitive content. Synthese, 190(1), 79–102.CrossRefGoogle Scholar
Ruitenburg, W. (1984). On the period of sequences $\left({a}^n(p)\right)$ in intuitionistic propositional calculus. Journal of Symbolic Logic, 49(3), 892–899.CrossRefGoogle Scholar
Sikorski, R. (1969). Boolean Algebras. Berlin: Springer-Verlag.CrossRefGoogle Scholar
Wronski, A. (1973). Intermediate logics and the disjunction property. Reports on Mathematical Logic, 1, 39–51.Google Scholar
Yang, F., & Väänänen, J. (2016). Propositional logics of dependence. Annals of Pure and Applied Logic, 167(7), 557–589.CrossRefGoogle Scholar