Abstract
Résumés
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 117-118
-
- Article
-
- You have access
- Export citation
Front matter
LER volume 79 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Research Article
On Cobb-Douglas Preferences in Bilateral Oligopoly
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 89-110
-
- Article
- Export citation
Abstract
Résumés
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 127-128
-
- Article
-
- You have access
- Export citation
Front matter
LER volume 79 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. f1-f5
-
- Article
-
- You have access
- Export citation
LER volume 79 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Abstract
Summaries
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 111-113
-
- Article
-
- You have access
- Export citation
Back matter
LER volume 79 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Abstract
Résumés
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 114-116
-
- Article
-
- You have access
- Export citation
Back matter
LER volume 79 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation
LER volume 79 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
LER volume 79 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back matter
LER volume 79 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 August 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

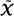 (
(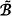 (X). The analysis of these two partial games takes into account competition
(X). The analysis of these two partial games takes into account competition