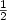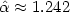Special issue dedicated to the 12th "Journées Montoises d'Informatique Théorique"
Introduction
Foreword
-
- Published online by Cambridge University Press:
- 11 February 2010, p. 1
-
- Article
- Export citation
Research Article
Morphisms fixing words associated with exchange of three intervals
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 3-17
-
- Article
- Export citation
Radix enumeration of rational languages
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 19-36
-
- Article
- Export citation
On the computation of covert channel capacity
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 37-58
-
- Article
- Export citation
How to build billiard words using decimations
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 59-77
-
- Article
- Export citation
Formal language properties of hybrid systems with strong resets
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 79-111
-
- Article
- Export citation
Infinite words containing squares at every position
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 113-124
-
- Article
- Export citation
On the number of squares in partial words
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 125-138
-
- Article
- Export citation
The critical exponent of the Arshon words
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 139-150
-
- Article
- Export citation
Binary words avoiding the pattern AABBCABBA
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 151-158
-
- Article
- Export citation
Standard factors of Sturmian words
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 159-174
-
- Article
- Export citation
On the growth rates of complexity of threshold languages
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 175-192
-
- Article
- Export citation