Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shur, Arseny M.
2010.
Developments in Language Theory.
Vol. 6224,
Issue. ,
p.
411.
Shur, Arseny M.
2010.
Computer Science – Theory and Applications.
Vol. 6072,
Issue. ,
p.
350.
SHUR, ARSENY M.
2011.
ON THE EXISTENCE OF MINIMAL β-POWERS.
International Journal of Foundations of Computer Science,
Vol. 22,
Issue. 07,
p.
1683.
Shur, Arseny M.
2011.
Developments in Language Theory.
Vol. 6795,
Issue. ,
p.
28.
Gorbunova, Irina A.
and
Shur, Arseny M.
2011.
On Pansiot Words Avoiding 3-Repetitions.
Electronic Proceedings in Theoretical Computer Science,
Vol. 63,
Issue. ,
p.
138.
Tunev, Igor N.
and
Shur, Arseny M.
2012.
Mathematical Foundations of Computer Science 2012.
Vol. 7464,
Issue. ,
p.
800.
GORBUNOVA, IRINA A.
and
SHUR, ARSENY M.
2012.
ON PANSIOT WORDS AVOIDING 3-REPETITIONS.
International Journal of Foundations of Computer Science,
Vol. 23,
Issue. 08,
p.
1583.
Shur, Arseny M.
2012.
Growth properties of power-free languages.
Computer Science Review,
Vol. 6,
Issue. 5-6,
p.
187.
Shur, Arseny M.
2014.
Growth of Power-Free Languages over Large Alphabets.
Theory of Computing Systems,
Vol. 54,
Issue. 2,
p.
224.
Ochem, Pascal
Rao, Michaël
and
Rosenfeld, Matthieu
2018.
Sequences, Groups, and Number Theory.
p.
177.
Shallit, Jeffrey
and
Shur, Arseny
2019.
Subword complexity and power avoidance.
Theoretical Computer Science,
Vol. 792,
Issue. ,
p.
96.
Petrova, Elena A.
and
Shur, Arseny M.
2021.
Branching Densities of Cube-Free and Square-Free Words.
Algorithms,
Vol. 14,
Issue. 4,
p.
126.
Petrova, Elena A.
and
Shur, Arseny M.
2021.
Developments in Language Theory.
Vol. 12811,
Issue. ,
p.
328.
Dvořáková, L'ubomíra
Pelantová, Edita
Opočenská, Daniela
and
Shur, Arseny M.
2022.
On minimal critical exponent of balanced sequences.
Theoretical Computer Science,
Vol. 922,
Issue. ,
p.
158.
Shur, Arseny M.
2023.
Developments in Language Theory.
Vol. 13911,
Issue. ,
p.
219.
Shur, Arseny M.
2024.
Non-Constructive Upper Bounds for Repetition Thresholds.
Theory of Computing Systems,
Vol. 68,
Issue. 6,
p.
1487.
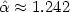 as k tends to infinity.
as k tends to infinity.

