Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T22:57:53.189Z Has data issue: false hasContentIssue false
  • English
  • Français

On-line finite automata for addition in some numeration systems

Published online by Cambridge University Press:  15 August 2002

Christiane Frougny
Christiane Frougny*
Affiliation:
Université Paris VIII and L.I.A.F.A., Case 7014, 2 place Jussieu, 75251 Paris Cedex 05, France; [email protected].
Get access

Abstract

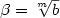We consider numeration systems where the base is anegative integer, or a complex number which is a root of anegative integer.We give parallel algorithms for addition in these numeration systems,from which we derive on-line algorithms realized by finite automata. A general construction relating addition in base βand addition in base βm is given.Results on addition in base $\beta=\sqrt[m]{b}$ , where b is a relative integer, follow.We also show that addition in base the golden ratiois computable by an on-line finite automaton, but is notparallelizable.

Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 33 , Issue 1 , January 1999 , pp. 79 - 101
Copyright
© EDP Sciences, 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouche, J.-P., Cateland, E., Gilbert, W.J., Peitgen, H.-O., Shallit, J.O. and Skordev, G., Automatic maps in exotic numeration systems. Theory Comput. Syst. 30 (1997) 285-331. CrossRef
T. Aoki, H. Amada and T. Higuchi, Real/complex reconfigurable arithmetic using redundant complex number systems, in Proc. 13th Symposium on Computer Arithmetic (1997) 200-207.
Avizienis, A., Signed-digit number representations for fast parallel arithmetic. IEE Trans. Electron. Comput. 10 (1961) 389-400. CrossRef
M.P. Béal, Codage symbolique, Masson (1993).
J. Berstel, Transductions and Context-free Languages, Teubner (1979).
J. Berstel, Fonctions rationnelles et addition. Actes de l'École de Printemps de Théorie des Langages, LITP (1982) 177-183.
J. Berstel, Fibonacci words -- A survey, The book of L, Springer-Verlag (1986) 13-27.
C.Y. Chow and J.E. Robertson, Logical design of a redundant binary adder, in Proc. 4th Symposium on Computer Arithmetic (1978) 109-115.
Choffrut, C., Une caractérisation des fonctions séquentielles et des fonctions sous-séquentielles en tant que relations rationnelles. Theoret. Comput. Sci. 5 (1977) 325-337. CrossRef
J. Duprat, Y. Herreros and S. Kla, New redundant representations of complex numbers and vectors. IEE Trans. Comput. C-42 (1993) 817-824.
S. Eilenberg, Automata, languages and machines, Vol. A (Academic Press, 1974).
M.D. Ercegovac, On-line arithmetic: An overview. Real time Signal Processing VII SPIE 495 (1984) 86-93.
Frougny, Ch., Confluent linear numeration systems. Theoret. Comput. Sci. 106 (1992) 183-219. CrossRef
Frougny, Ch., Representation of numbers and finite automata. Math. Systems Theory 25 (1992) 37-60. CrossRef
Frougny, Ch., Parallel and on-line addition in negative base and some complex number systems, in Proc. of the Conference Euro-Par 96, Springer, Lyon, L.N.C.S. 1124 (1996) 175-182.
Ch. Frougny, J. Sakarovitch, Synchronisation déterministe des automates à délai borné. Theoret. Comput. Sci. 191 (1998) 61-77. CrossRef
Gilbert, W., Radix representations of quadratic fields. J. Math. Anal. Appl. 83 (1981) 264-274. CrossRef
Y. Herreros, Contribution à l'arithmétique des ordinateurs, Ph.D. Dissertation, I.N.P.G., Grenoble, France (1991).
Kátai, I. and Szabó, J., Canonical number systems. Acta Sci. Math. 37 (1975) 255-280.
Knuth, D.E., An imaginary number system. CACM 3 (1960) 245-247. CrossRef
D.E. Knuth, The art of computer programming, Seminumerical Algorithms, Vol. 2, 2nd ed. (Addison-Wesley, 1988).
S. Körmendi, Classical number systems in $\mbox{\boldmath{\bf Q}}[\sqrt[3]{2}]$ .Acta Sci. Math. 50 (1986) 351-357.
D. Lind and B. Marcus, An introduction to symbolic dynamics and coding, Cambridge University Press (1995).
Matula, D.W., Basic digit sets for radix representation. JACM 29 (1982) 1131-1143. CrossRef
Muller, J.-M., Some characterizations of functions computable in on-line arithmetic. IEE Trans. Comput. 43 (1994) 752-755. CrossRef
A.M. Nielsen and J.-M. Muller, Borrow-save adders for real and complex number systems, in Proc. of the Conference Real Numbers and Computers, Marseille (1996) 121-137.
Pekmestzi, K., Complex numbers multipliers. IEE Proc. Computers and Digital Techniques 136 (1989) 70-75. CrossRef
Penney, W., A ``binary" system for complex numbers. JACM 12 (1965) 247-248. CrossRef
A. Rényi, Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957) 477-493.
Robert, A., A good basis for computing with complex numbers. El. Math. 49 (1994) 111-117.
Safer, T., Radix representations of algebraic number fields and finite automata, in Proc. Stacs'98, LNCS 1373 (1998) 356-365.
K.S. Trivedi and M.D. Ercegovac, On-line algorithms for division and multiplication. IEE Trans. Comput. C 26 (1977) 681-687.
Vaysse, O., Addition molle et fonctions p-locales. Semigroup Forum 34 (1986) 157-175. CrossRef