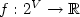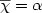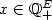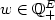This paper is devoted to the exact resolution of a strongly NP-hard resource-constrained scheduling problem, the Process Move Programming problem, which arises in relation to the operability of certain high-availability real-time distributed systems. Based on the study of the polytope defined as the convex hull of the incidence vectors of the admissible process move programs, we present a branch-and-cut algorithm along with extensive computational results demonstrating its practical relevance, in terms of both exact and approximate resolution when the instance size increases.

The minimum cost multiple-source unsplittable flow problem isstudied in this paper. A simple necessary condition to get asolution is proposed. It deals with capacities and demands and canbe seen as a generalization of the well-known semi-metriccondition for continuous multicommdity flows. A cutting planealgorithm is derived using a superadditive approach. Theinequalities considered here are valid for single knapsackconstraints. They are based on nondecreasing superadditivefunctions and can be used to strengthen the relaxation of anyinteger program with knapsack constraints. Some numericalexperiments confirm the efficiency of the inequalities introducedin the paper.

Given a graph G = (V,E) and a “cost function” $f: 2^V\rightarrow\mathbb{R}$ 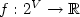(provided by an oracle), the problem [PCliqW] consists in finding a partition into cliques of V(G) of minimum cost. Here, the cost of a partition is the sum of the costs of the cliques in the partition.We provide a polynomial time dynamic program for the case where G is an interval graph and f belongs to a subclass of submodular set functions, which we call “value-polymatroidal”.This provides a common solution for various generalizations of the coloringproblem in co-interval graphs such as max-coloring,“Greene-Kleitman's dual”, probabilist coloring and chromatic entropy. In the last two cases, this is the first polytime algorithm for co-interval graphs. In contrast, NP-hardness of related problems is discussed. We also describe an ILP formulation for [PCliqW] which gives a common polyhedral framework to express min-max relations such as ${\overline{\chi}}=\alpha$ 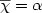for perfect graphs and the polymatroid intersection theorem. This approach allows to provide a min-max formula for [PCliqW] if G is the line-graph of a bipartite graph and f is submodular.However, this approach fails to provide a min-max relation for [PCliqW] if G is an interval graphs and f is value-polymatroidal.


Clique family inequalities a∑v∈W xv + (a - 1)∈v∈W , xv ≤ aδ form an intriguing class of valid inequalities for the stable set polytopes of all graphs. We prove firstly that their Chvátal-rank is at most a, which provides an alternative proof for the validity of clique family inequalities, involving only standard rounding arguments.Secondly, we strengthen the upper bound further and discuss consequences regarding the Chvátal-rank of subclasses of claw-free graphs.


A co-biclique of a simple undirected graph G = (V,E) is the edge-set of two disjoint complete subgraphs of G.(A co-biclique is the complement of a biclique.)A subset F ⊆ E is an independent of G if there is a co-biclique B such that F ⊆ B, otherwise F is a dependent of G. This paper describes the minimal dependents of G. (A minimal dependent is a dependent C such that any proper subset of C is an independent.) It is showed that a minimum-cost dependent set of G can be determined in polynomial time for any nonnegative cost vector $x\in \mathbb Q_+^E$ . Based on this, we obtain a branch-and-cut algorithm for the maximum co-biclique problem which is, given a weight vector $w\in \mathbb Q_+^E$ , to find a co-biclique B of G maximizing w(B) = ∑e∈B we .

Given a weighted undirected graph G = (V,E),a tree (respectively tour) cover of an edge-weighted graph is a set of edges which forms a tree (resp. closed walk) and covers every other edge in the graph. The tree (resp. tour) cover problem is of finding a minimum weight tree (resp. tour) cover of G. Arkin, Halldórsson and Hassin (1993) give approximation algorithms with factors respectively 3.5 and 5.5. Later Könemann, Konjevod, Parekh, and Sinha (2003) study the linear programming relaxations and improve both factors to 3. We describe in the first part of the paper a 2-approximation algorithm for the metric case of tree cover.In the second part, we will consider a generalized version of tree (resp. tour) covers problem which is to find a minimum tree (resp. tours) which covers a subset D ⊆ E of G.We show that the algorithms of Könemann et al.can be adapted for the generalized tree and tours covers problem with the same factors.

The m-subspace polytope is defined as the convex hull of the characteristic vectors of all m-dimensional subspaces ofa finite affine space. The particular case of the hyperplane polytopehas been investigated by Maurras (1993) and Anglada and Maurras (2003), who gave a complete characterization of the facets. The general m-subspace polytope that we consider shows a much more involved structure, notably as regards facets. Nevertheless, several families of facets are established here. Then the group of automorphisms of the m-subspace polytope is completely described and the adjacency of vertices is fully characterized.