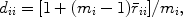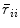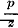Several theorems concerning properties of the communaltiy of a test in the Thurstone multiple factor theory are established. The following theorems are applicable to a battery of n tests which are describable in terms of r common factors, with orthogonal reference vectors.

1. The communality of a test j is equal to the square of the multiple correlation of test j with the r reference vectors.

2. The communality of a test j is equal to the square of the multiple correlation of test j with the r reference vectors and the n—1 remaining tests.

Corollary: The square of the multiple correlation of a test j with the n—1 remaining tests is equal to or less than the communality of test j. It cannot exceed the communality.

3. The square of the multiple correlation of a test j with the n—1 remaining tests equals the communality of test j if the group of tests contains r statistically independent ests teach with a communality of unity.

4. With correlation coefficients corrected for attenuation, when the number of tests increases indefinitely while the rank of the correlational matrix remains unchanged, the communality of a test j equals the square of the multiple correlation of test j with the n—1 remaining tests.

5. With raw correlation coefficients, it is shown in a special case that the square of the multiple correlation of a test j with the n—1 remaining tests approaches the communality of test j as a limit when the number of tests increases indefinitely while the rank of correlational matrix remains the same. This has not yet been proved for the general case.

The topological concepts allow us to assign individuals and goals to certain spatial regions. They allow us to designate what locomotions are possible for an individual and what regions must be traversed in attaining a definite goal. But the topological concepts alone tell us nothing of the actual locomotions performed in psychological activities. So far we have seen that the position of the individual at the start of the psychological activity may be defined in reference to this. Psychological activities may be ordered to locomotions. The individual in this sense has the character of a thing. The space through which the locomotion occurs has the properties of a medium. (Cf. Heider (10). In physical problems where the field construct is used, one may make this same distinction. Bodies falling in the earth’s gravitational field have the properties of things, while the atmosphere is to be characterized as a medium. Similarly in the electro-static field, the isolated conductors have the properties of things and the field has those of a medium.

Given s fallible tests t1,t2, …ts, the problem is to express their intercorrelations in terms of the average correlations between a varying number of parallel forms contained within each test. A new correlation determinant Δ′ is derived containing dii instead of unity as an element on the principal diagonal, where

\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$d_{ii} = [1 + (m_i - 1)\bar r_{ii} ]/m_i ,$$\end{document}

\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\bar r_{ii} $$\end{document}

In continuation of a previous paper, some consequences of the fundamental equations established there are studied. For some simple hypothetical cases it is shown how some of the parameters which enter in the equations governing the structure of the social group can be determined by means of those equations from actually observable data. Furthermore some general properties of the variation with respect to time of the fundamental distribution function, which enters in the equations, are derived.

Using scores of 1200 students on a long test as a criterion, each of five subtests of different difficulty has maximum correlation with the criterion when the criterion is dichotomized at a value appropriate to the difficulty of the subtest. A 50-item test element is scored on an all-or-none basis with different standards for passing, and the percentage of passes for successive points on the criterion variable is computed. The Constant Method is applied to this relationship. The limen thus computed is a measure of difficulty, the dispersion is a measure of average (or total) validity, and the slope of the curve is a measure of differential validity. The difficulty of a test element is thus directly related to the maximum differential validity.

By the use of an algebraic variant of the ordinary formula for bi-serial correlation, tables, and graphic devices, a time-saving systematic procedure for the computation of bi-serial correlation co-efficients is outlined for application to the evaluation of items of a test. A table of for arguments of p=.000 to p=.999 is given.

The widespread use of bi-serial r in item analysis makes a quick and accurate method of evaluating the formula desirable. Such a method is provided by homographs. Dunlap and Kurtz in their Nomograph No. 47 give a method of solving the better known statement of the formula, namely (1)