1. Introduction
Psychometric investigation on cognitive ability and speed has a long and rich history (e.g., Carroll Reference Carroll1993; Gulliksen Reference Gulliksen1950; Luce Reference Luce1986; Thorndike et al. Reference Thorndike, Bregman, Cobb and Woodyard1926). In the Reference Thorndike, Bregman, Cobb and Woodyard1926 monograph, Thorndike et al. stated that “level”, “extent”, and “speed” are three distinct aspects in any measure of performance: While both “level” and “extent” are manifested by correctness of answers and thus can be collectively translated to ability in modern terminology, “the speed of producing any given product is defined, of course, by the time required” (Thorndike et al. Reference Thorndike, Bregman, Cobb and Woodyard1926, p. 26). The prevalence of computerized test administration and data collection in recent years facilitates the acquisition of response-time (RT) data at the level of individual test items. In parallel, we witnessed a mushrooming development of psychometric models for item responses and RT over the past few decades (see De Boeck & Jeon, Reference De Boeck and Jeon2019; Goldhammer, Reference Goldhammer2015, for reviews), which in turn gave rise to broader investigations on the relationship between response speed and accuracy in various substantive domains (see Lee & Chen, Reference Lee and Chen2011; Kyllonen & Zu, Reference Kyllonen and Zu2016; von Davier et al., Reference von Davier, Khorramdel, He, Shin and Chen2019, for reviews). Empirical findings suggested that response speed not only composes proficiency or informs the construct to be measured but also bespeaks secondary test-taking behaviors such as rapid guessing (Deribo et al., Reference Deribo, Kroehne and Goldhammer2021; Wise, Reference Wise2017), using preknowledge (Qian et al., Reference Qian, Staniewska, Reckase and Woo2016; Sinharay, Reference Sinharay2020; Sinharay and Johnson, Reference Sinharay and Johnson2020), lacking motivation (Finn, Reference Finn2015; Thurstone, Reference Thurstone1937; Wise and Kong, Reference Wise and Kong2005), etc.
Characterizing individual differences in ability and speed with item responses and RT data is in essence a factor analysis problem (Molenaar et al., Reference Molenaar, Tuerlinckx and van der Maas2015a, Reference Molenaar, Tuerlinckx and van der Maasb). The two-factor simple-structure model proposed by van der Linden (Reference van der Linden2007) was arguably the most popular modeling option so far: Item responses and log-transformed RT variables are treated as two independent clusters of observed indicators for the ability and speed/slowness factors, respectively, and the two latent factors jointly follow a bivariate normal distribution (see Fig. 2 of Molenaar et al., Reference Molenaar, Tuerlinckx and van der Maas2015a, for a path-diagram representation). A notable merit of the simple-structure factor model is its plug-and-play nature: Analysts can separately apply standard item response theory (IRT) models for discrete responses (e.g., one-, two-, three-, or four- parameter logistic [1-4PL] model; Birnbaum, Reference Birnbaum1968; Barton & Lord, Reference Barton and Lord1981) and standard factor analysis models for the continuous log-RT variables (e.g., linear-normal factor model; Jöreskog, Reference Jöreskog1969), and then simply let the two latent factors covary. Despite its succinctness and popularity, the simple-structure model may fit poorly to empirical data. A highly endorsed interpretation for the lack of fit is that the two inter-dependent latent factors cannot fully explain the dependencies among item-level responses and RT variables. Based on this rationale, numerous diagnostics for residual dependencies and remedial modifications of the simple-structure model have been proposed in the recent literature (e.g., Bolsinova et al., Reference Bolsinova, De Boeck and Tijmstra2017; Bolsinova & Maris, Reference Bolsinova and Maris2016; Bolsinova & Molenaar, Reference Bolsinova and Molenaar2018; Bolsinova et al., Reference Bolsinova, Tijmstra and Molenaar2017; Bolsinova & Tijmstra, Reference Bolsinova and Tijmstra2016; Glas & van der Linden, Reference Glas and van der Linden2010; Meng et al., Reference Meng, Tao and Chang2015; Ranger & Ortner, Reference Ranger and Ortner2012; van der Linden & Glas, Reference van der Linden and Glas2010).
Augmenting standard IRT models with a measurement component for item-level RT may result in more precise ability scores, which is often highlighted as a practical benefit of RT modeling in educational assessment (Bolsinova and Tijmstra, Reference Bolsinova and Tijmstra2018; van der Linden et al., Reference van der Linden, Klein Entink and Fox2010). Under a simple-structure model with bivariate normal factors, the degree to which item-level RT improves scoring precision is dictated by the strength of the inter-factor correlation (see Study 1 of van der Linden et al., Reference van der Linden, Klein Entink and Fox2010). However, near-zero correlation estimates between ability and speed were sometimes encountered in real-world applications (e.g., Bolsinova, De Boeck, & Tijmstra, Reference Bolsinova, De Boeck and Tijmstra2017; Bolsinova, Tijmstra, & Molenaar, Reference Bolsinova, Tijmstra and Molenaar2017; Lee & Jia, Reference Lee and Jia2014; van der Linden, Scrams, & Schnipke, Reference van der Linden, Scrams and Schnipke1999). Whenever it happens, analysts are inclined to conclude that item-level RT is not useful for ability estimation at all, or that a less parsimonious factor structure is needed to enhance the utility of RT for scoring purposes (e.g., allowing the log-RT variables to cross-load on the ability factor; Bolsinova & Tijmstra, Reference Bolsinova and Tijmstra2018).
Indeed, van der Linden’s (Reference van der Linden2007) model could be overly restrictive for analyzing item responses and RT data. We, however, do not want to rush to the conclusion that it is the simple factor structure that should be blamed and abandoned. Other parametric assumptions, such as link functions, linear or curvilinear dependencies, and distributions of latent traits and error terms, are also part of the model specification and may contribute to the misfit as well. A fair evaluation on the tenability and usefulness of a simple factor structure demands a version of the model with minimal parametric assumptions other than the simple factor structure itself, which we refer to as a semiparametric simple-structure model. Should the semiparametric model still struggle to fit the data adequately, we no longer hesitate to give up on the simple factor structure.
Fortunately, the major components of a semiparametric simple-structure factor analysis have been readily developed in the existing literature. They are
-
1. A semiparametric (unidimensional) IRT model for dichotomous and polytomous responses (Abrahamowicz and Ramsay, Reference Abrahamowicz and Ramsay1992; Rossi et al., Reference Rossi, Wang and Ramsay2002);
-
2. A semiparametric (unidimensional) factor model for continuous log-RT variables (Liu and Wang, Reference Liu and Wang2022)
-
3. A nonparametric copula density estimator for ability and speed/slowness with fixed marginals (Kauermann et al., Reference Kauermann, Schellhase and Ruppert2013; Dou et al., Reference Dou, Kuriki, Lin and Richards2021).
As a side remark, we are aware of alternative semiparametric approaches that can be used for each of the above three components: for example, the monotonic polynomial logistic model for item responses (Falk and Cai, Reference Falk and Cai2016a, Reference Falk and Caib), the proportional hazard model (Kang, Reference Kang2017; Ranger and Kuhn, Reference Ranger and Kuhn2012; Wang et al., Reference Wang, Fan, Chang and Douglas2013b) and the linear transformation model (Wang et al., Reference Wang, Chang and Douglas2013a) for item-level RT, and the finite normal mixture model (Bauer, Reference Bauer2005; Pek et al., Reference Pek, Sterba, Kok and Bauer2009) and the Davidian curve model (Woods and Lin, Reference Woods and Lin2009; Zhang and Davidian, Reference Zhang and Davidian2001; Zhang et al., Reference Zhang, Wang, Weiss and Tao2021) for the joint distribution of latent traits. However, we focus on methods based on smoothing splines in the current analysis. Besides, the simultaneous incorporation of flexible models for all the three components of a simple structure model appears to be novel in the literature of RT modeling. Compared to, e.g., Wang et al. (Reference Wang, Chang and Douglas2013a) and Wang et al. (Reference Wang, Fan, Chang and Douglas2013b), in which semiparametric models were applied to only the RT data, our model fares more flexible and thus is more likely to reveal sophisticated dependency patterns in a joint analysis of item responses and RT data.
By retrospectively analyzing a set of mathematics testing data from the 2015 Programme for International Student Assessment (PISA; OECD, 2016), we revisit the following research questions that have only been partially answered previously through parametric simple-structure models:
-
(1) Is a simple factor structure sufficient for a joint analysis of item response and RT?
-
(2) How strong are math ability and general processing speed associated in the population of respondents?
-
(3) To what extent can processing speed improve the precision in ability estimates under a simple-structure model?
It is worth mentioning that the data set was previously analyzed by Zhan et al. (Reference Zhan, Liao and Bian2018) using a variant of van der Linden’s (Reference van der Linden2007) simple-structure model with testlet effects: A higher-order cognitive diagnostics model with testlet effects was used for item responses, a linear-normal factor model was used for log-transformed RT, and the (higher-order) ability and speed factors were assumed to be bivariate normal. Zhan et al. (Reference Zhan, Liao and Bian2018) reported an estimated inter-factor correlation of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.2$$\end{document}
![]() and hence concluded that the association between speed and ability is weak. We are particularly interested in whether their conclusion stands after abandoning inessential parametric assumptions other than the simple factor structure.
and hence concluded that the association between speed and ability is weak. We are particularly interested in whether their conclusion stands after abandoning inessential parametric assumptions other than the simple factor structure.
The rest of the paper is organized as follows. We first provide a technical introduction of the proposed semiparametric procedure in Sect. 2: The three components of the semiparametric simple-structure model are formulated in Sects. 2.1 and 2.2, penalized maximum likelihood (PML) estimation and empirical selection of penalty weights are outlined in Sect. 2.3, and bootstrap-based goodness-of-fit assessment and inferences are described in Sects. 2.4 and 2.5. Descriptive statistics for the 2015 PISA mathematics data and a plan of our analysis are summarized in Sect. 3, followed by a detailed report of results in Sect. 4. The paper concludes with a discussion of broader implications of our findings and limitations of our method.
2. Methods
2.1. Unidimensional Semiparametric Factor Models
Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}\in {\mathcal {Y}}_j\subset {\mathbb {R}}$$\end{document}
![]() be the jth manifest variable (MV) observed for respondent i:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
be the jth manifest variable (MV) observed for respondent i:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
![]() represents either a discrete response to a test item or a continuous item-level RT. In our semiparametric factor model, the distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
represents either a discrete response to a test item or a continuous item-level RT. In our semiparametric factor model, the distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
![]() is characterized by the following logistic conditional densityFootnote 1 of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij} = y\in {\mathcal {Y}}_j$$\end{document}
is characterized by the following logistic conditional densityFootnote 1 of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij} = y\in {\mathcal {Y}}_j$$\end{document}
![]() given a unidimensional latent variable (LV; also known as latent factor, latent trait, etc.)
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_i = x\in {\mathcal {X}}\subset {\mathbb {R}}$$\end{document}
given a unidimensional latent variable (LV; also known as latent factor, latent trait, etc.)
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_i = x\in {\mathcal {X}}\subset {\mathbb {R}}$$\end{document}
![]() :
:
in which the normalizing integral with respect to the dominating measure
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _j$$\end{document}
![]() on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathcal {Y}}_j$$\end{document}
on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathcal {Y}}_j$$\end{document}
![]() is assumed to be finite. Equation 1 defines a valid conditional density as it is non-negative and integrates to unity with respect to y for a given x. However, the bivariate function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j: {\mathcal {X}}\times {\mathcal {Y}}_j\rightarrow {\mathbb {R}}$$\end{document}
is assumed to be finite. Equation 1 defines a valid conditional density as it is non-negative and integrates to unity with respect to y for a given x. However, the bivariate function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j: {\mathcal {X}}\times {\mathcal {Y}}_j\rightarrow {\mathbb {R}}$$\end{document}
![]() is not identifiable: It is not difficult to see that adding any univariate function of x to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j(x, y)$$\end{document}
is not identifiable: It is not difficult to see that adding any univariate function of x to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j(x, y)$$\end{document}
![]() does not change the value of Eq. 1 (Gu, Reference Gu1995, Reference Gu2013). To impose necessary identification constraints, we re-write
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j$$\end{document}
does not change the value of Eq. 1 (Gu, Reference Gu1995, Reference Gu2013). To impose necessary identification constraints, we re-write
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j$$\end{document}
![]() by the functional analysis of variance (fANOVA) decomposition
by the functional analysis of variance (fANOVA) decomposition
and require that
for some reference levels
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_0\in {\mathcal {X}}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y_0\in {\mathcal {Y}}_j$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y_0\in {\mathcal {Y}}_j$$\end{document}
![]() . Equation 3 is referred to as side conditions;
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_0$$\end{document}
. Equation 3 is referred to as side conditions;
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_0$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y_0$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y_0$$\end{document}
![]() can be set arbitrarily within the respective domains (see Liu & Wang, Reference Liu and Wang2022, for more detailed comments). The univariate component
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^y$$\end{document}
can be set arbitrarily within the respective domains (see Liu & Wang, Reference Liu and Wang2022, for more detailed comments). The univariate component
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^y$$\end{document}
![]() and the bivariate component
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^{xy}$$\end{document}
and the bivariate component
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^{xy}$$\end{document}
![]() are functional parameters to be estimated from observed data.
are functional parameters to be estimated from observed data.
Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\psi }_j: {\mathcal {Y}}_j\rightarrow {\mathbb {R}}^{L_j}$$\end{document}
![]() be a collection of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L_j$$\end{document}
be a collection of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L_j$$\end{document}
![]() basis functions defined on the support of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
basis functions defined on the support of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\varphi }: {\mathcal {X}}\rightarrow {\mathbb {R}}^K$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\varphi }: {\mathcal {X}}\rightarrow {\mathbb {R}}^K$$\end{document}
![]() be a collection of K basis functions defined on the support of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_i$$\end{document}
be a collection of K basis functions defined on the support of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_i$$\end{document}
![]() . We proceed to approximate the functional parameters by basis expansion. In particular, we set the univariate component
. We proceed to approximate the functional parameters by basis expansion. In particular, we set the univariate component
in which the coefficient vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_j\in {\mathbb {R}}^{L_j}$$\end{document}
![]() satisfies
satisfies
Similarly, the bivariate component is expressed as
in which the coefficient matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j\in {\mathbb {R}}^{L_j\times K}$$\end{document}
![]() satisfies
satisfies
The linear constraints imposed for the coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_j$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
![]() (Eqs. 5 and 7) guarantee that the side conditions (Eq. 3) are satisfied.
(Eqs. 5 and 7) guarantee that the side conditions (Eq. 3) are satisfied.
Continuous Data When both
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_i\in {\mathcal {X}}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}\in {\mathcal {Y}}_j$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}\in {\mathcal {Y}}_j$$\end{document}
![]() (equipped with the Lebesgue measure
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _j$$\end{document}
(equipped with the Lebesgue measure
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _j$$\end{document}
![]() ) are continuous random variables defined on closed intervals, Eq. 1 corresponds to the semiparametric factor model considered by Liu and Wang (Reference Liu and Wang2022). Without loss of generality, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathcal {X}}= {\mathcal {Y}}_j = [0, 1]$$\end{document}
) are continuous random variables defined on closed intervals, Eq. 1 corresponds to the semiparametric factor model considered by Liu and Wang (Reference Liu and Wang2022). Without loss of generality, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathcal {X}}= {\mathcal {Y}}_j = [0, 1]$$\end{document}
![]() . In fact, any closed interval can be rescaled to the unit interval via a linear transform: If
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$z\in [a, b]$$\end{document}
. In fact, any closed interval can be rescaled to the unit interval via a linear transform: If
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$z\in [a, b]$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a < b$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a < b$$\end{document}
![]() , then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(z - a)/(b - a)\in [0, 1]$$\end{document}
, then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(z - a)/(b - a)\in [0, 1]$$\end{document}
![]() . To approximate smooth functional parameters supported on unit intervals or squares, we use the same cubic B-spline basis with equally spaced knots (De Boor, Reference De Boor1978) for both
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\psi }_j$$\end{document}
. To approximate smooth functional parameters supported on unit intervals or squares, we use the same cubic B-spline basis with equally spaced knots (De Boor, Reference De Boor1978) for both
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\psi }_j$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\varphi }$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\varphi }$$\end{document}
![]() (and thus
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L_j = K$$\end{document}
(and thus
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L_j = K$$\end{document}
![]() ). It is sometimes desirable to force the MV to be stochastically increasing as the LV increases. Liu and Wang (Reference Liu and Wang2022) considered a simple approach to impose likelihood-ratio monotonicity, which boils down to the following linear inequality constraints on the coefficient matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
). It is sometimes desirable to force the MV to be stochastically increasing as the LV increases. Liu and Wang (Reference Liu and Wang2022) considered a simple approach to impose likelihood-ratio monotonicity, which boils down to the following linear inequality constraints on the coefficient matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
![]() :
:
In Eq. 8,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\hbox {vec}(\cdot )$$\end{document}
![]() denotes the vectorization operator, and
denotes the vectorization operator, and

is a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(K - 1)\times K$$\end{document}
![]() first-order difference matrix. We also set
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{D}}_1 = 1$$\end{document}
first-order difference matrix. We also set
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{D}}_1 = 1$$\end{document}
![]() by convention.
by convention.
Discrete Data When
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathcal {Y}}_j = \{0, \dots , C_j - 1\}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _j$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _j$$\end{document}
![]() is the associated counting measure, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y_0 = 0$$\end{document}
is the associated counting measure, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y_0 = 0$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L_j = C_j - 1$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$L_j = C_j - 1$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\psi }_j(y) = (\psi _{j1}(y), \dots , \psi _{j,C_j-1}(y))^\top $$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\psi }_j(y) = (\psi _{j1}(y), \dots , \psi _{j,C_j-1}(y))^\top $$\end{document}
![]() such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\psi _{jk}(y) = 1$$\end{document}
such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\psi _{jk}(y) = 1$$\end{document}
![]() if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y = k$$\end{document}
if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y = k$$\end{document}
![]() and 0 if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y\ne k$$\end{document}
and 0 if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y\ne k$$\end{document}
![]() . Then our generic model (Eqs. 1 and 2) reduces to Abrahamowicz and Ramsay’s (1992) multi-categorical semiparametric IRT model for unordered polytomous responses, which is further equivalent to the semiparametric logistic IRT proposed by Ramsay and Winsberg (Reference Ramsay and Winsberg1991) and Rossi et al. (Reference Rossi, Wang and Ramsay2002) when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$C_j = 2$$\end{document}
. Then our generic model (Eqs. 1 and 2) reduces to Abrahamowicz and Ramsay’s (1992) multi-categorical semiparametric IRT model for unordered polytomous responses, which is further equivalent to the semiparametric logistic IRT proposed by Ramsay and Winsberg (Reference Ramsay and Winsberg1991) and Rossi et al. (Reference Rossi, Wang and Ramsay2002) when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$C_j = 2$$\end{document}
![]() (i.e., dichotomous data). It is because the basis expansions (i.e., Eqs. 4 and 6) are simplified to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^y(y) = \alpha _{jy}$$\end{document}
(i.e., dichotomous data). It is because the basis expansions (i.e., Eqs. 4 and 6) are simplified to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^y(y) = \alpha _{jy}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^{xy}(x, y) = \varvec{\varphi }(x)^\top \varvec{\beta }_{jy}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^{xy}(x, y) = \varvec{\varphi }(x)^\top \varvec{\beta }_{jy}$$\end{document}
![]() , in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }_{jy}^\top $$\end{document}
, in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }_{jy}^\top $$\end{document}
![]() denotes the yth row of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
denotes the yth row of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
![]() , if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y = 1, \dots , C_j - 1$$\end{document}
, if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y = 1, \dots , C_j - 1$$\end{document}
![]() ; meanwhile,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^y(0) = 0$$\end{document}
; meanwhile,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^y(0) = 0$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^{xy}(x, 0)\equiv 0$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^{xy}(x, 0)\equiv 0$$\end{document}
![]() as part of the side conditions. The conditional density (e.g., Eq. 1) then becomes the item response function (IRF)
as part of the side conditions. The conditional density (e.g., Eq. 1) then becomes the item response function (IRF)
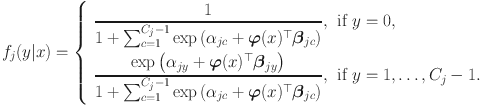
Like the continuous case, we only consider
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathcal {X}}= [0, 1]$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\varphi }$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\varphi }$$\end{document}
![]() being a cubic B-spline basis defined by a sequence of equally spaced knots. Similar to Eq. 8 in the continuous case, we may impose likelihood-ratio monotonicity on the conditional density by
being a cubic B-spline basis defined by a sequence of equally spaced knots. Similar to Eq. 8 in the continuous case, we may impose likelihood-ratio monotonicity on the conditional density by
which reduces to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{D}}_k\varvec{\beta }_{j1}\ge \textbf{0}$$\end{document}
![]() when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$C_j = 2$$\end{document}
when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$C_j = 2$$\end{document}
![]() (i.e., dichotomous items).
(i.e., dichotomous items).
2.2. Simple Factor Structure and Latent Variable Density
Consider a battery of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_1$$\end{document}
![]() continuous MVs and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_2$$\end{document}
continuous MVs and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_2$$\end{document}
![]() discrete MVs and write
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m = m_1 + m_2$$\end{document}
discrete MVs and write
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m = m_1 + m_2$$\end{document}
![]() . We typically have
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_1 = m_2 = m/2$$\end{document}
. We typically have
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_1 = m_2 = m/2$$\end{document}
![]() when the discrete responses and continuous RT variables are observed for the same set of items. From now on, denote by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i1}, \dots , Y_{i,m_1}$$\end{document}
when the discrete responses and continuous RT variables are observed for the same set of items. From now on, denote by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i1}, \dots , Y_{i,m_1}$$\end{document}
![]() the base-10 log-transformed RT, each of which is rescaled to [0, 1], and by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i, m_1+1}, \dots , Y_{im}$$\end{document}
the base-10 log-transformed RT, each of which is rescaled to [0, 1], and by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i, m_1+1}, \dots , Y_{im}$$\end{document}
![]() the corresponding responses. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}, X_{i2}\in [0, 1]$$\end{document}
the corresponding responses. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}, X_{i2}\in [0, 1]$$\end{document}
![]() be the slowness
Footnote 2 and ability factors for respondent i, respectively. A simple factor structure requires that the item responses
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i,m_1+1}, \dots , Y_{im}$$\end{document}
be the slowness
Footnote 2 and ability factors for respondent i, respectively. A simple factor structure requires that the item responses
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i,m_1+1}, \dots , Y_{im}$$\end{document}
![]() are conditionally independent of the slowness factor
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
are conditionally independent of the slowness factor
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
![]() given the ability factor
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
given the ability factor
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
![]() , and symmetrically that the log-RT variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i1}, \dots , Y_{i,m_1}$$\end{document}
, and symmetrically that the log-RT variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i1}, \dots , Y_{i,m_1}$$\end{document}
![]() are independent of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
are independent of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
![]() given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
![]() . We also make the local independence assumption that is standard in factor analysis (McDonald, Reference McDonald1982):
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i1}, \dots , Y_{im}$$\end{document}
. We also make the local independence assumption that is standard in factor analysis (McDonald, Reference McDonald1982):
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{i1}, \dots , Y_{im}$$\end{document}
![]() are mutually independent conditional on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
are mutually independent conditional on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
![]() . Further let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{Y}}_i = (Y_{i1}, \dots , Y_{im})^\top $$\end{document}
. Further let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{Y}}_i = (Y_{i1}, \dots , Y_{im})^\top $$\end{document}
![]() collect all the MVs produced by respondent i. The simple structure and local independence assumptions imply that
collect all the MVs produced by respondent i. The simple structure and local independence assumptions imply that
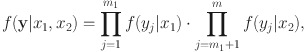
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}= (y_1, \dots , y_m)^\top \in [0, 1]^{m_1}\times {\mathcal {Y}}_{m_1 + 1}\times \cdots \times {\mathcal {Y}}_{m}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_1, x_2\in [0, 1]$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_1, x_2\in [0, 1]$$\end{document}
![]() .
.
For convenience in approximating functional parameters, both
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
![]() are assumed to follow a Uniform[0, 1] distribution marginally. However, we are aware that uniformly distributed LVs are less attractive for substantive interpretation. Adopting the strategy of Liu and Wang (Reference Liu and Wang2022), we define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{id}^* = \Phi ^{-1}(X_{id})$$\end{document}
are assumed to follow a Uniform[0, 1] distribution marginally. However, we are aware that uniformly distributed LVs are less attractive for substantive interpretation. Adopting the strategy of Liu and Wang (Reference Liu and Wang2022), we define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{id}^* = \Phi ^{-1}(X_{id})$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d = 1, 2$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d = 1, 2$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Phi ^{-1}$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Phi ^{-1}$$\end{document}
![]() is the standard normal quantile function; the transformed LVs are marginally
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{N}(0, 1)$$\end{document}
is the standard normal quantile function; the transformed LVs are marginally
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal{N}(0, 1)$$\end{document}
![]() variates, in agreement with the standard formulation in parametric factor analysis. To capture the potentially complex association between latent slowness and ability, we employ a nonparametric estimator for the copula density (Sklar, Reference Sklar1959; Nelsen, Reference Nelsen2006) of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(X_{i1}, X_{i2})^\top $$\end{document}
variates, in agreement with the standard formulation in parametric factor analysis. To capture the potentially complex association between latent slowness and ability, we employ a nonparametric estimator for the copula density (Sklar, Reference Sklar1959; Nelsen, Reference Nelsen2006) of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(X_{i1}, X_{i2})^\top $$\end{document}
![]() , denoted
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c(x_1, x_2)$$\end{document}
, denoted
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c(x_1, x_2)$$\end{document}
![]() . A copula density is non-negative and has uniform marginals: That is,
. A copula density is non-negative and has uniform marginals: That is,
c is in fact the joint density of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(X_{i1}, X_{i2})^\top $$\end{document}
![]() since both
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
since both
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}$$\end{document}
![]() are marginally uniform. In the light of Sklar’s theorem, the joint density of the transformed
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(X_{i1}^*, X_{i2}^*)^\top $$\end{document}
are marginally uniform. In the light of Sklar’s theorem, the joint density of the transformed
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(X_{i1}^*, X_{i2}^*)^\top $$\end{document}
![]() can be calculated by
can be calculated by
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\phi $$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Phi $$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Phi $$\end{document}
![]() are the density and distribution functions of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{{\mathcal {N}}}}(0, 1)$$\end{document}
are the density and distribution functions of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{{\mathcal {N}}}}(0, 1)$$\end{document}
![]() , respectively.
, respectively.
We approximate the bivariate copula density c by a tensor-product spline (Dou et al., Reference Dou, Kuriki, Lin and Richards2021; Kauermann et al., Reference Kauermann, Schellhase and Ruppert2013):
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\varphi }: [0, 1]\rightarrow {\mathbb {R}}^K$$\end{document}
![]() is a set of cubic B-spline basis functions defined with equally spaced knotsFootnote 3, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbf {\Xi }$$\end{document}
is a set of cubic B-spline basis functions defined with equally spaced knotsFootnote 3, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbf {\Xi }$$\end{document}
![]() is an
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K\times K$$\end{document}
is an
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K\times K$$\end{document}
![]() coefficient matrix. For Eq. 14 to be a proper copula density, we impose the following linear constraints on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbf {\Xi }$$\end{document}
coefficient matrix. For Eq. 14 to be a proper copula density, we impose the following linear constraints on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbf {\Xi }$$\end{document}
![]() :
:
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\xi _{kl}$$\end{document}
![]() is the (k, l)th element of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbf {\Xi }$$\end{document}
is the (k, l)th element of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbf {\Xi }$$\end{document}
![]() , and
, and
is a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K\times 1$$\end{document}
![]() vector of normalizing constants for basis functions. It can be verified by elementary properties of B-splines and straightforward algebra that Eqs. 14 and 15 imply Eq. 12.
vector of normalizing constants for basis functions. It can be verified by elementary properties of B-splines and straightforward algebra that Eqs. 14 and 15 imply Eq. 12.
2.3. Estimation
For each MV
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j = 1,\dots , m$$\end{document}
![]() , let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }_j = (\varvec{\alpha }_j^\top , \hbox {vec}({\textbf{B}}_j)^\top )^\top $$\end{document}
, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }_j = (\varvec{\alpha }_j^\top , \hbox {vec}({\textbf{B}}_j)^\top )^\top $$\end{document}
![]() collect all the coefficients in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^y$$\end{document}
collect all the coefficients in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^y$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^{xy}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g_j^{xy}$$\end{document}
![]() . Also let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }= (\varvec{\theta }_j^\top , \dots , \varvec{\theta }_m^\top , \hbox {vec}(\mathbf {\Xi })^\top )^\top $$\end{document}
. Also let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }= (\varvec{\theta }_j^\top , \dots , \varvec{\theta }_m^\top , \hbox {vec}(\mathbf {\Xi })^\top )^\top $$\end{document}
![]() denote all the coefficients in the simple-structure factor model. We estimate
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }$$\end{document}
denote all the coefficients in the simple-structure factor model. We estimate
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }$$\end{document}
![]() by penalized maximum (marginal) likelihood (PML). The marginal likelihood for the MV vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{Y}}_i = {\textbf{y}}$$\end{document}
by penalized maximum (marginal) likelihood (PML). The marginal likelihood for the MV vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{Y}}_i = {\textbf{y}}$$\end{document}
![]() amounts to the integration of Eq. 11 over
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_1$$\end{document}
amounts to the integration of Eq. 11 over
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_1$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_2$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_2$$\end{document}
![]() under the copula density
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c(x_1, x_2)$$\end{document}
under the copula density
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$c(x_1, x_2)$$\end{document}
![]() : That is,
: That is,
Pooling across an independent and identically distributed (i.i.d.) sample of size n, we arrive at the sample log-likelihood function
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_{1:n} = ({\textbf{y}}_1, \dots , {\textbf{y}}_n)^\top $$\end{document}
![]() denotes an
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$n\times m$$\end{document}
denotes an
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$n\times m$$\end{document}
![]() matrix of observed MV data.
matrix of observed MV data.
To avoid overfitting, we regularize the roughness of estimated functional parameters by quadratic-form penalties in spline coefficients. For a continuous MV j, the penalty term for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }_j$$\end{document}
![]() is the sum of a univariate P-spline penalty for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_j$$\end{document}
is the sum of a univariate P-spline penalty for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_j$$\end{document}
![]() and a bivariate P-spline penalty for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
and a bivariate P-spline penalty for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
![]() (Eilers and Marx, Reference Eilers and Marx1996; Currie et al., Reference Currie, Durban and Eilers2006):
(Eilers and Marx, Reference Eilers and Marx1996; Currie et al., Reference Currie, Durban and Eilers2006):
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _j > 0$$\end{document}
![]() is the penalty weight,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{I}}_K$$\end{document}
is the penalty weight,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{I}}_K$$\end{document}
![]() denotes a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K\times K$$\end{document}
denotes a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K\times K$$\end{document}
![]() identity matrix, and
identity matrix, and
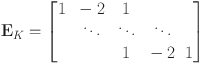
is a second-order difference matrix of dimension
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(K - 2)\times K$$\end{document}
![]() . If the MV is polytomous, no penalty is needed for the intercepts
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_j$$\end{document}
. If the MV is polytomous, no penalty is needed for the intercepts
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_j$$\end{document}
![]() and columns of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
and columns of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{B}}_j$$\end{document}
![]() . The resulting P-spline penalty term then becomes
. The resulting P-spline penalty term then becomes
A similar bivariate P-spline penalty is also introduced for the coefficient matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbf {\Xi }$$\end{document}
![]() :
:
with a positive penalty weight
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{m+1}$$\end{document}
![]() . Combining Eqs. 18–21, we express the penalized sample log-likelihood function as
. Combining Eqs. 18–21, we express the penalized sample log-likelihood function as
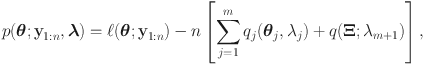
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }= (\lambda _1, \dots , \lambda _m, \lambda _{m+1})^\top \in (0, \infty )^{m + 1}$$\end{document}
![]() . PML estimation amounts to finding
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }$$\end{document}
. PML estimation amounts to finding
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }$$\end{document}
![]() that maximizes Eq. 22 subject to a series of linear equality and inequality constraints (i.e., Eqs. 5, 7, 8, 10, and 15), which is accomplished by a modified expectation-maximization (EM; Bock & Aitkin, Reference Bock and Aitkin1981; Dempster et al., Reference Dempster, Laird and Rubin1977) algorithm. A sequential quadratic programming algorithm (Nocedal & Wright, Reference Nocedal and Wright2006, Algorithm 18.3) is employed in the M-step to handle constrained optimization. The algorithm is a simple extension to what was described in Sects. 4.1 and 4.2 of Liu and Wang (Reference Liu and Wang2022); further details are therefore omitted for succinctness. Denote by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{\varvec{\theta }}}}({\textbf{y}}_{1:n}, \varvec{\lambda })$$\end{document}
that maximizes Eq. 22 subject to a series of linear equality and inequality constraints (i.e., Eqs. 5, 7, 8, 10, and 15), which is accomplished by a modified expectation-maximization (EM; Bock & Aitkin, Reference Bock and Aitkin1981; Dempster et al., Reference Dempster, Laird and Rubin1977) algorithm. A sequential quadratic programming algorithm (Nocedal & Wright, Reference Nocedal and Wright2006, Algorithm 18.3) is employed in the M-step to handle constrained optimization. The algorithm is a simple extension to what was described in Sects. 4.1 and 4.2 of Liu and Wang (Reference Liu and Wang2022); further details are therefore omitted for succinctness. Denote by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{\varvec{\theta }}}}({\textbf{y}}_{1:n}, \varvec{\lambda })$$\end{document}
![]() the PML estimates of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }$$\end{document}
the PML estimates of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }$$\end{document}
![]() obtained from data
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_{1:n}$$\end{document}
obtained from data
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_{1:n}$$\end{document}
![]() and penalty weights
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
and penalty weights
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
![]() .
.
Larger penalty weights enforce less variable yet more biased solutions and vice versa—a well-known phenomenon referred to as the bias-variance trade-off. To strike a balance, we select the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
![]() from a pre-specified grid by multi-fold cross-validation. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _1, \dots , \Omega _S$$\end{document}
from a pre-specified grid by multi-fold cross-validation. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _1, \dots , \Omega _S$$\end{document}
![]() be a partition of the sample:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bigcup _{s=1}^S\Omega _s = \{1, \dots , n\}$$\end{document}
be a partition of the sample:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bigcup _{s=1}^S\Omega _s = \{1, \dots , n\}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _s\cap \Omega _{s'} = \emptyset $$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _s\cap \Omega _{s'} = \emptyset $$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s\ne s'$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s\ne s'$$\end{document}
![]() . For each s, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _s^c$$\end{document}
. For each s, let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _s^c$$\end{document}
![]() be the calibration set and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _s$$\end{document}
be the calibration set and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _s$$\end{document}
![]() be the validation set, in which the superscript c denotes the complement of a set. Predictive adequacy associated with a particular
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
be the validation set, in which the superscript c denotes the complement of a set. Predictive adequacy associated with a particular
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
![]() is gauged by the empirical risk
is gauged by the empirical risk
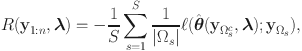
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$|\Omega _s|$$\end{document}
![]() denotes the size of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _s$$\end{document}
denotes the size of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Omega _s$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ell ({{\hat{\varvec{\theta }}}}({\textbf{y}}_{\Omega _s^c}, \varvec{\lambda }); {\textbf{y}}_{\Omega _s})$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ell ({{\hat{\varvec{\theta }}}}({\textbf{y}}_{\Omega _s^c}, \varvec{\lambda }); {\textbf{y}}_{\Omega _s})$$\end{document}
![]() denotes the log-likelihood of the validation sub-sample evaluated at the estimated coefficients from the calibration set. Instead of choosing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
denotes the log-likelihood of the validation sub-sample evaluated at the estimated coefficients from the calibration set. Instead of choosing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
![]() that minimizes Eq. 23 (i.e., the best solution), we adopt the “one standard error (SE)” heuristic (Chen and Yang, Reference Chen and Yang2021; Hastie et al., Reference Hastie, Tibshirani and Friedman2009) to take into account sampling variability: We select the smoothest solution within one SE from the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
that minimizes Eq. 23 (i.e., the best solution), we adopt the “one standard error (SE)” heuristic (Chen and Yang, Reference Chen and Yang2021; Hastie et al., Reference Hastie, Tibshirani and Friedman2009) to take into account sampling variability: We select the smoothest solution within one SE from the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
![]() that minimizes the empirical risk, where the SE at a specific
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
that minimizes the empirical risk, where the SE at a specific
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
![]() is estimated by
is estimated by
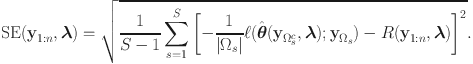
The value
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }$$\end{document}
![]() contains
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m + 1$$\end{document}
contains
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m + 1$$\end{document}
![]() elements. To alleviate the computational burden for penalty weights selection, we set
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _1 = \cdots = \lambda _{m_1} = \lambda
_{(c)}$$\end{document}
elements. To alleviate the computational burden for penalty weights selection, we set
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _1 = \cdots = \lambda _{m_1} = \lambda
_{(c)}$$\end{document}
![]() for continuous MVs,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{m_1 + 1} = \cdots = \lambda _m = \lambda _{(d)}$$\end{document}
for continuous MVs,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{m_1 + 1} = \cdots = \lambda _m = \lambda _{(d)}$$\end{document}
![]() for discrete MVs, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{m + 1} = \lambda _{(g)}$$\end{document}
for discrete MVs, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{m + 1} = \lambda _{(g)}$$\end{document}
![]() for the copula density of the two LVs. We also resort to a multistage workaround to select the remaining three penalty weights: (1) A unidimensional model is fitted to only the continuous MVs to find the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
for the copula density of the two LVs. We also resort to a multistage workaround to select the remaining three penalty weights: (1) A unidimensional model is fitted to only the continuous MVs to find the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
![]() , (2) a unidimensional model is fitted to only the discrete MVs to find the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
, (2) a unidimensional model is fitted to only the discrete MVs to find the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
![]() , and (3) a two-dimensional simple-structure model is fitted to all the MVs to find the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
, and (3) a two-dimensional simple-structure model is fitted to all the MVs to find the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
![]() while fixing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
while fixing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
![]() at their optimal values determined in earlier stages. The optimal weights thereby selected are denoted
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
at their optimal values determined in earlier stages. The optimal weights thereby selected are denoted
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
![]() . We then refit the model using the optimal weight and the full set of data to obtain the final solution of spline coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{\varvec{\theta }}}}({\textbf{y}}_{1:n}, {{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n}))$$\end{document}
. We then refit the model using the optimal weight and the full set of data to obtain the final solution of spline coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{\varvec{\theta }}}}({\textbf{y}}_{1:n}, {{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n}))$$\end{document}
![]() .
.
2.4. Model Fit Diagnostics and Inferences
We quantify the sampling variability of sample statistics, including goodness of fit diagnostics and approximations to functional parameters, by bootstrapping (Efron and Tibshirani, Reference Efron and Tibshirani1994; Hastie et al., Reference Hastie, Tibshirani and Friedman2009). Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\bar{{\textbf{Y}}}}}_i$$\end{document}
![]() be a random sample from the collection of observed MV vectors
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{{\textbf{y}}_1, \dots , {\textbf{y}}_n\}$$\end{document}
be a random sample from the collection of observed MV vectors
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{{\textbf{y}}_1, \dots , {\textbf{y}}_n\}$$\end{document}
![]() such that each element is selected with probability 1/n. Sample with replacement n times and denote the resulting bootstrap sample
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\bar{{\textbf{Y}}}}}_{1:n}$$\end{document}
such that each element is selected with probability 1/n. Sample with replacement n times and denote the resulting bootstrap sample
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\bar{{\textbf{Y}}}}}_{1:n}$$\end{document}
![]() . We approximate the sampling distribution of any test statistic
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T({\textbf{Y}}_{1:n})$$\end{document}
. We approximate the sampling distribution of any test statistic
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T({\textbf{Y}}_{1:n})$$\end{document}
![]() by the bootstrap sampling distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T({{\bar{{\textbf{Y}}}}}_{1:n})$$\end{document}
by the bootstrap sampling distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$T({{\bar{{\textbf{Y}}}}}_{1:n})$$\end{document}
![]() conditional on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_{1:n}$$\end{document}
conditional on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_{1:n}$$\end{document}
![]() . Note that most of the test statistics under investigation depend on the optimal penalty weights
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
. Note that most of the test statistics under investigation depend on the optimal penalty weights
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
![]() , which is a function of the observed data. Pilot runs suggest that the variability of the optimal weights is small over bootstrap samples; we therefore treat
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }= {{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
, which is a function of the observed data. Pilot runs suggest that the variability of the optimal weights is small over bootstrap samples; we therefore treat
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }= {{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
![]() as fixed and do not repeat penalty weight selection in the resampling process, which substantially reduces computational time.
as fixed and do not repeat penalty weight selection in the resampling process, which substantially reduces computational time.
Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{ij} = \varsigma _j(Y_{ij})$$\end{document}
![]() be the MV score associated with the individual response entry
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
be the MV score associated with the individual response entry
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
![]() . For continuous log-RT variables and dichotomous items, we simply let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j$$\end{document}
. For continuous log-RT variables and dichotomous items, we simply let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j$$\end{document}
![]() be the identity function and thus
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{ij} = Y_{ij}$$\end{document}
be the identity function and thus
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S_{ij} = Y_{ij}$$\end{document}
![]() ; for unordered polytomous items, however, a customized
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j$$\end{document}
; for unordered polytomous items, however, a customized
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j$$\end{document}
![]() function is needed for recoding raw responses to a more meaningful scale (see Sect. 3.3 for an example). To assess the lack-of-fit for the simple-structure semiparametric model—in particular the unaccounted dependencies residing in observed MVs, we compute the residual correlation statistic
function is needed for recoding raw responses to a more meaningful scale (see Sect. 3.3 for an example). To assess the lack-of-fit for the simple-structure semiparametric model—in particular the unaccounted dependencies residing in observed MVs, we compute the residual correlation statistic
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j, j' = 1,\dots , m$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j < j'$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j < j'$$\end{document}
![]() . In Eq. 25,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$r_{jj'}$$\end{document}
. In Eq. 25,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$r_{jj'}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\rho _{jj'}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\rho _{jj'}$$\end{document}
![]() are the respective sample and model-implied correlations between the jth and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j'$$\end{document}
are the respective sample and model-implied correlations between the jth and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j'$$\end{document}
![]() th MV scores: The model-implied correlation can be further expressed as
th MV scores: The model-implied correlation can be further expressed as
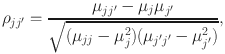
in which we drop the dependency on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }$$\end{document}
![]() for conciseness. In Eq. 26, the first moment
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _j$$\end{document}
for conciseness. In Eq. 26, the first moment
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _j$$\end{document}
![]() can be computed as
can be computed as
There are three cases when computing the second moment
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mu _{jj'}$$\end{document}
![]() : (1) for a single MV, i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j = j'$$\end{document}
: (1) for a single MV, i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j = j'$$\end{document}
![]() ,
,
(2) when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\ne j'$$\end{document}
![]() but the two MVs load on the same LV,
but the two MVs load on the same LV,
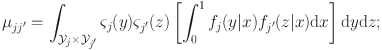
and (3) when the jth and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j'$$\end{document}
![]() th MVs load respectively on the first and second LVs,
th MVs load respectively on the first and second LVs,
2.5. Latent Variable Density and Scores
As we have mentioned in Sect. 2.2, inferences for LVs are made based on the marginally normal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}^*$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}^*$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}^*$$\end{document}
![]() . In particular, we are interested in the strength of association between the two LVs. To this end, we compute the coefficient of determination for predicting ability (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X^*_{i2}$$\end{document}
. In particular, we are interested in the strength of association between the two LVs. To this end, we compute the coefficient of determination for predicting ability (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X^*_{i2}$$\end{document}
![]() ) by slowness (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X^*_{i1}$$\end{document}
) by slowness (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X^*_{i1}$$\end{document}
![]() ):
):
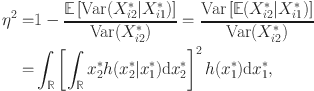
in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$h(x_d^*) = \int _{{\mathbb {R}}} h(x_1^*, x_2^*)\hbox {d}x^*_{3-d}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d = 1, 2$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d = 1, 2$$\end{document}
![]() , is the marginal density of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{id}^*$$\end{document}
, is the marginal density of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{id}^*$$\end{document}
![]() (assumed to be standard normal), and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$h(x_2^*|x_1^*) = h(x_1^*, x_2^*) / h(x_1^*)$$\end{document}
(assumed to be standard normal), and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$h(x_2^*|x_1^*) = h(x_1^*, x_2^*) / h(x_1^*)$$\end{document}
![]() is the conditional density of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_2^*$$\end{document}
is the conditional density of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_2^*$$\end{document}
![]() given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_1^*$$\end{document}
given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_1^*$$\end{document}
![]() . Equation 31 reduces to the usual coefficient of determination for linear models when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(X_{i1}^*, X_{i2}^*)^\top $$\end{document}
. Equation 31 reduces to the usual coefficient of determination for linear models when
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(X_{i1}^*, X_{i2}^*)^\top $$\end{document}
![]() follows a bivariate normal distribution. When analyzing real data, we evaluate
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2$$\end{document}
follows a bivariate normal distribution. When analyzing real data, we evaluate
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2$$\end{document}
![]() using the estimated LV density, denoted
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\hat{\eta }}^2({\textbf{y}}_{1:n}, \varvec{\lambda })$$\end{document}
using the estimated LV density, denoted
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\hat{\eta }}^2({\textbf{y}}_{1:n}, \varvec{\lambda })$$\end{document}
![]() ; the sampling variability of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\hat{\eta }}^2({\textbf{y}}_{1:n}, \varvec{\lambda })$$\end{document}
; the sampling variability of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\hat{\eta }}^2({\textbf{y}}_{1:n}, \varvec{\lambda })$$\end{document}
![]() is again characterized by bootstrapping (Sect. 2.4).
is again characterized by bootstrapping (Sect. 2.4).
For each respondent i, LV scores can be predicted based on the posterior distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(X_{i1}^*, X_{i2}^*)^\top $$\end{document}
![]() given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_i = {\textbf{y}}$$\end{document}
given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_i = {\textbf{y}}$$\end{document}
![]() with density
with density
The means of the posterior distribution are often referred to as the expected a posteriori (EAP) scores, and the corresponding standard deviations (SDs) gauge the precision of the EAP scores (Thissen and Wainer, Reference Thissen and Wainer2001). In practice, density functions involved in Eq. 32 must be estimated from sample data, which introduces additional uncertainty to scores computed from the estimated posterior. Better precision measures can be obtained from a predictive distribution of LV scores (Liu and Yang, Reference Liu and Yang2018a, Reference Liu and Yangb; Yang et al., Reference Yang, Hansen and Cai2012). Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\hat{f}}}^h(x_1^*, x_2^*|{\textbf{y}}; {\textbf{y}}_{1:n}, \varvec{\lambda })$$\end{document}
![]() be the estimated posterior density. The bootstrap expectation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathbb {E}}{{\hat{f}}}^h(x_1^*, x_2^*|{\textbf{y}}; {{\bar{{\textbf{Y}}}}}_{1:n}, \varvec{\lambda })$$\end{document}
be the estimated posterior density. The bootstrap expectation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathbb {E}}{{\hat{f}}}^h(x_1^*, x_2^*|{\textbf{y}}; {{\bar{{\textbf{Y}}}}}_{1:n}, \varvec{\lambda })$$\end{document}
![]() with respect to the (random) bootstrap sample
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\bar{{\textbf{Y}}}}}_{1:n}$$\end{document}
with respect to the (random) bootstrap sample
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${{\bar{{\textbf{Y}}}}}_{1:n}$$\end{document}
![]() defines a suitable predictive density; the inverse variance of the predictive distribution, which is henceforth referred to as the predictive precision, can be conveniently estimated from a collection of bootstrap samples. To set the baseline for assessing the gain in predictive precision, we also consider the marginal posterior density of the ability factor
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}^*$$\end{document}
defines a suitable predictive density; the inverse variance of the predictive distribution, which is henceforth referred to as the predictive precision, can be conveniently estimated from a collection of bootstrap samples. To set the baseline for assessing the gain in predictive precision, we also consider the marginal posterior density of the ability factor
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}^*$$\end{document}
![]() :
:
Estimated marginal EAP scores and the associated bootstrap predictive precisions can be obtained in a fashion similar to the two-dimensional case.
3. Data and Analysis Plan
3.1. PISA 2015 Mathematics Data
The data we analyze next came from the PISA 2015 computer-based mathematics assessment (OECD, 2016). The test is composed of 17 dichotomously scored items from two mathematics testing clusters (M1 and M2). Similar to the Zhan et al. (Reference Zhan, Liao and Bian2018), we only retained cases with complete response entries, leading to a total number of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$n = 8606$$\end{document}
![]() observations from 58 countries/economies.
observations from 58 countries/economies.
Among the 17 items, there are four testlets (with item labels starting with CM155, CM411, CM496, and CM564), each of which involves a pair of items. We collapsed the two items within each testlet into a single four-category nominal item: The four categories 0, 1, 2, and 3 indicated the original item response patterns (0, 0), (1, 0), (0, 1), and (1, 1), respectively. The corresponding RT entries were also summed to a single testlet-level RT variable. Accordingly, the number of items involved in the initial fitting is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_1 = m_2 = 13$$\end{document}
![]() , and the number of MVs is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m = 26$$\end{document}
, and the number of MVs is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m = 26$$\end{document}
![]() . During data preprocessing, we identified a number of extremely small and large RT entries, which are potential outliers and may cause instability in model fitting. Therefore, we excluded for each MV the top and bottom 1% RT and the associated item response dataFootnote 4. Then we took the base-10 logarithm of the RT variables and rescaled them to the unit interval. Selected descriptive statistics of the final data can be found in Tables 1 and 2.
. During data preprocessing, we identified a number of extremely small and large RT entries, which are potential outliers and may cause instability in model fitting. Therefore, we excluded for each MV the top and bottom 1% RT and the associated item response dataFootnote 4. Then we took the base-10 logarithm of the RT variables and rescaled them to the unit interval. Selected descriptive statistics of the final data can be found in Tables 1 and 2.
Table 1 Descriptive statistics for transformed response time (RT).
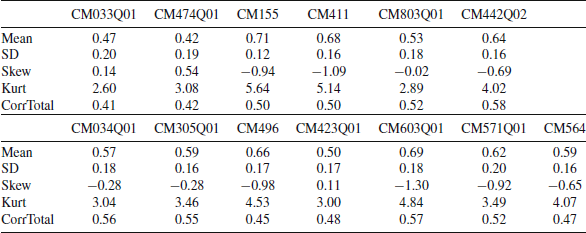
For CM155, CM411, CM496, and CM564, summary statistics are computed for the log-transformed RT of the testlets. SD: Standard deviation. Skew: Skewness. Kurt: Kurtosis. CorrTotal: Correlation with the total sum of log-RT.
We applied the based-10 logarithm to the raw RT data and then rescaled the log-transformed variables to [0, 1].
Table 2 Descriptive statistics for item responses.
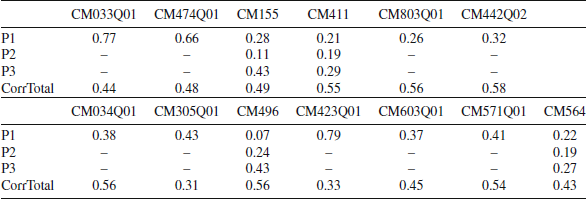
For testlets CM155, CM411, CM496, and CM564, the original item response patterns (0, 0), (1, 0), (0, 1), and (1, 1) are recoded to 0, 1, 2, and 3, respectively. P1–3: Observed proportions of response categories 1–3. CorrTotal: Correlation with total score; we apply the scoring function described in Sect. 3.3 to the testlet MVs before computing the total score.
3.2. Analysis Plan
As we have mentioned in Sect. 1, the data set was analyzed in the previous work by Zhan et al. (Reference Zhan, Liao and Bian2018) using a parametric simple-structure model. Though we acknowledge the parsimony and thus retain a simple factor structure, our analysis differs substantially from the previous work, because we model MV-LV and LV-LV dependencies in a nonparametric fashion and are able to provide an ultimate assessment for the validity of a simple factor structure in this data set. Once we confirm that the dependencies in the MVs are sufficiently accounted for, we present graphics and statistics based on the fitted model to demonstrate how the respective distributions of item responses and RT are governed by the ability and slowness factors, as well as how ability and slowness covary in the population of respondents.
Major steps of our analysis are outlined as follows.
-
step 1. Determine the optimal penalty weights \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
 by the three-stage procedure described in Sect. 2.3.
by the three-stage procedure described in Sect. 2.3. -
step 2. Draw \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$B = 100$$\end{document}
 bootstrap samples (i.e., resample with replacement) from the observed data
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_{1:n}$$\end{document}
bootstrap samples (i.e., resample with replacement) from the observed data
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\textbf{y}}_{1:n}$$\end{document}
 and repeat model fitting in each bootstrap sample with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }= {{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
and repeat model fitting in each bootstrap sample with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\lambda }= {{\hat{\varvec{\lambda }}}}({\textbf{y}}_{1:n})$$\end{document}
 .
. -
step 3. Examine the residual correlation statistics (Eq. 25) for all pairs of MVs. Flag a pair if the 90% two-sided bootstrap CI for the residual correlation fall entirely above 0.1 or below \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$-0.1$$\end{document}
 .
. -
step 4. Remove problematic items from the test and repeat steps 1–3 until no large residual correlation remains.
-
step 5. Plot the conditional densities of the MVs given the marginally normal LVs (Eq. 1 with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$x = \Phi (x^*)$$\end{document}
 ) and the joint density of the two LVs (Eq. 13). Compute estimated
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2$$\end{document}
) and the joint density of the two LVs (Eq. 13). Compute estimated
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2$$\end{document}
 statistics (Eq. 31), EAP scores, and the associated predictive SDs for the scores.
statistics (Eq. 31), EAP scores, and the associated predictive SDs for the scores.
Per the request from two referees, we also report in the supplementary document the empirical risk statistics and density estimates for two parametric models. The first model is a standard baseline model for the joint analysis of item response and RT data, which features linear-normal factor models for log-RT variables, 2PL models for item responses, nominal response models for testlets, and a bivariate normal LV density. Due to the strong parametric assumptions made therein, we do not expect the baseline model to fit the data well. Inspired by the semiparametric fitting, we also specified an updated parametric model with nonlinear factor models with quintic mean functions for log-RT variables, 4PL models for item responses, nominal models for testlets, and a two-component normal mixture density for the LVs. Even though the updated model has yet to attain a fit comparable to the semiparametric model, it reproduces key functional patterns in the semiparametric estimates of the bivariate LV density and the conditional densities for the MVs. Despite being tangential to the specific aims of the present work, these additional analyses exemplify another standard usage of semiparametric/nonparametric models: to provide diagnostic information about model-data fit and to guide model modification.
3.3. Detailed Configuration
For replicability, we provide all the tuning details involved in our analysis. PML estimation of the semiparametric simple structure model was implemented in the R package spfa, which can be downloaded at https://github.com/wwang1370/spfa and https://cran.r-project.org/web/packages/spfa/index.html.
Estimation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K = 13$$\end{document}
![]() B-splines basis functions were used for approximating smooth functions defined on the unit interval. Each log-RT variable was linearly transformed to [0, 1] using the sample minimum and maximum. The reference level for LVs and continuous MVs was set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_0 = y_0 = 0.5$$\end{document}
B-splines basis functions were used for approximating smooth functions defined on the unit interval. Each log-RT variable was linearly transformed to [0, 1] using the sample minimum and maximum. The reference level for LVs and continuous MVs was set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$x_0 = y_0 = 0.5$$\end{document}
![]() ; for discrete MVs, the reference level was set to the first response category
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y_0 = 0$$\end{document}
; for discrete MVs, the reference level was set to the first response category
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$y_0 = 0$$\end{document}
![]() . We impose likelihood-ratio monotonicity on item CM442Q02 since both its responses and RT show the highest correlations with totals (see Tables 1 and 2). Intractable integrals appeared in the conditional densities (Eq. 1) were approximated by a 21-point Gauss-Legendre quadrature rescaled to the unit interval. The marginal likelihood function (Eq. 17) involves a two-dimensional integral over the unit square and was approximated by a tensor-product Gauss-Legendre quadrature. In each fitting, we executed the EM algorithm until the change in the penalized log-likelihood (i.e., Eq. 22) was less than
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-3}$$\end{document}
. We impose likelihood-ratio monotonicity on item CM442Q02 since both its responses and RT show the highest correlations with totals (see Tables 1 and 2). Intractable integrals appeared in the conditional densities (Eq. 1) were approximated by a 21-point Gauss-Legendre quadrature rescaled to the unit interval. The marginal likelihood function (Eq. 17) involves a two-dimensional integral over the unit square and was approximated by a tensor-product Gauss-Legendre quadrature. In each fitting, we executed the EM algorithm until the change in the penalized log-likelihood (i.e., Eq. 22) was less than
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-3}$$\end{document}
![]() between consecutive iterations.
between consecutive iterations.
Penalty Weight Selection We selected the three penalty weights
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
![]() from the following sequences of decreasing values:
from the following sequences of decreasing values:
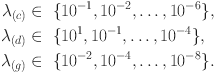
The empirical risk was computed by five-fold cross-validation (Eq. 23 with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S = 5$$\end{document}
![]() ). The smoothest solution within one SE (estimated by Eq. 24) from the minimal-risk solution was deemed optimal.
). The smoothest solution within one SE (estimated by Eq. 24) from the minimal-risk solution was deemed optimal.
Inference Conditional on the optimal penalty weights, we resampled
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$B = 100$$\end{document}
![]() times with replacement, refit the model in each bootstrap sample, and examine the bootstrap distributions of fitted densities and model fit statistics. When computing fit diagnostics and summary statistics, we approximated intractable integrals by the same quadrature systems that were used in parameter estimation. The MV scoring functionFootnote 5 for testlet responses was defined by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j(0) = 0$$\end{document}
times with replacement, refit the model in each bootstrap sample, and examine the bootstrap distributions of fitted densities and model fit statistics. When computing fit diagnostics and summary statistics, we approximated intractable integrals by the same quadrature systems that were used in parameter estimation. The MV scoring functionFootnote 5 for testlet responses was defined by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j(0) = 0$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j(1) = \varsigma _j(2) = 1$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j(1) = \varsigma _j(2) = 1$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j(3) = 2$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varsigma _j(3) = 2$$\end{document}
![]() .
.
4. Results
4.1. Model Fit and Modification
In the initial fitting of the semiparametric simple-structure model (using all 26 MVs), our cross-validation procedure selects
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-4}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-1}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-1}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-4}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-4}$$\end{document}
![]() as the respective optimal values for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
as the respective optimal values for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
![]() . A graphical display of the results can be found in the first row of Fig. 1.
. A graphical display of the results can be found in the first row of Fig. 1.

Figure 1 Empirical risks (Eq. 23) and standard errors (SE; Eq. 24). The rows of the graphical table correspond to the initial fitting (with all items) and the updated fitting (without the response time of CM034Q01 and CM571Q01). The columns represent the three stages of penalty weight selection (see Sect. 2.3). Within each panel, empirical risk values are plotted as functions of based-10 log-transformed penalty weights. Vertical bars indicate one SE above and below the empirical risk. The minimized empirical risks are shown as circles, while the optimal solutions determined by the “one SE rule” were highlighted as filled dots. The band formed by two horizontal dashed lines indicates the one-SE region associated with the minimum empirical risk. Note that the two graphs in the second column are identical: This is because all item responses are retained, and thus we do not need to re-select
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
![]() . LD: Local dependence.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
. LD: Local dependence.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
![]() : Penalty weights for continuous manifest variables (MVs), discrete MVs, and the latent density.
: Penalty weights for continuous manifest variables (MVs), discrete MVs, and the latent density.
Based on a full-data fitting with the optimal penalty weights, we summarize the residual correlation statistics (Eq. 25) for all pairs of MVs in a graphical table (Fig. 2). It is observed that dependencies within RT variables are well explained by the slowness factor, and similarly dependencies within item responses are well explained by the ability factor. The largest residual correlation in the left panel of Fig. 2 is 0.1 (between the log-RT of CM571Q01 and CM603Q01) with a 90% bootstrap CI [0.08, 0.12]. In contrast, we identify some non-ignorable residual dependencies between the log-RT and response of the same item (i.e., diagonal entries in the right panel of Fig. 2). The within-item residual correlations reach 0.14 (with a bootstrap CI [0.12, 0.15]) for both items CM034Q01 and CM571Q01. We also find a large negative residual correlation for item CM423Q1: The point estimate is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.12$$\end{document}
![]() , but the associated bootstrap CI
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.13, -0.1]$$\end{document}
, but the associated bootstrap CI
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.13, -0.1]$$\end{document}
![]() covers
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.1$$\end{document}
covers
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.1$$\end{document}
![]() . Meanwhile, the RT-response dependencies are well explained between items: The off-diagonal statistics in the right panel of Fig. 2 ranges between
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.07$$\end{document}
. Meanwhile, the RT-response dependencies are well explained between items: The off-diagonal statistics in the right panel of Fig. 2 ranges between
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.07$$\end{document}
![]() and 0.08.
and 0.08.

Figure 2 Residual correlation statistics for the initial fitting of the semiparametric simple-structure model. Left: Residual correlations between two log-transformed response time (log-RT) variables. Middle: Residual correlations between two item/testlet responses. Right: Residuals between a log-RT variable and a item/test response, in which rows represent log-RT variables and columns represent responses. Positive residual correlations are shown in red, while negative residual correlations are shown in blue. A darker color indicates a larger magnitude (Color figure online).
Given the above findings, we conclude that a simple factor structure largely suffices for modeling the item responses and RT in the 2015 PISA mathematics data. For two out of 13 items (CM034Q01 and CM571Q01), however, the associations between item-level response speed and accuracy are not fully addressed by individual differences in general processing speed and ability. To be clear of adverse impact caused by unaccounted residual dependencies, we dropped the log-RT variables for items CM034Q1 and CM571Q01 while letting their responses stay, which results in a modified simple-structure model with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_1 = 11$$\end{document}
![]() continuous MVs and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_2 = 13$$\end{document}
continuous MVs and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m_2 = 13$$\end{document}
![]() discrete ones. Steps 1–3 (see Sect. 3.2) were repeated. The optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
discrete ones. Steps 1–3 (see Sect. 3.2) were repeated. The optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(c)}$$\end{document}
![]() remains to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-4}$$\end{document}
remains to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-4}$$\end{document}
![]() , whereas the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
, whereas the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(g)}$$\end{document}
![]() increases to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-3}$$\end{document}
increases to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-3}$$\end{document}
![]() (see the second row of Fig. 1); the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)} = 10^{-1}$$\end{document}
(see the second row of Fig. 1); the optimal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\lambda _{(d)} = 10^{-1}$$\end{document}
![]() is retained as no change has been made to the item response variables. There is no more large residual this time. The ranges of the residual correlations are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.04, 0.08]$$\end{document}
is retained as no change has been made to the item response variables. There is no more large residual this time. The ranges of the residual correlations are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.04, 0.08]$$\end{document}
![]() among log-RT variables,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.03, 0.02]$$\end{document}
among log-RT variables,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.03, 0.02]$$\end{document}
![]() among response variables, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.11, 0.08]$$\end{document}
among response variables, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.11, 0.08]$$\end{document}
![]() across responses and log-RT. Similar to the initial fitting, the only residual correlation beyond
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pm 0.1$$\end{document}
across responses and log-RT. Similar to the initial fitting, the only residual correlation beyond
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pm 0.1$$\end{document}
![]() is observed between the response and log-RT of item CM423Q1; however, the 90% bootstrap CI of the statistic is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.13, -0.09]$$\end{document}
is observed between the response and log-RT of item CM423Q1; however, the 90% bootstrap CI of the statistic is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[-0.13, -0.09]$$\end{document}
![]() which contains
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.1$$\end{document}
which contains
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.1$$\end{document}
![]() . Therefore, we proceed to interpret the fitted densities based on the updated fitting.
. Therefore, we proceed to interpret the fitted densities based on the updated fitting.
4.2. Conditional Densities of Manifest Variables
Estimated conditional densities and means of the log-RT variables given the slowness factor are plotted in Fig. 3. Two major patterns are of interest here. First, although the high and low ends of the LV scale roughly map onto the longest and shortest RT for a majority of items/testlets, which justifies our decision to label the LV as “slowness”, the conditional mean function appears to decrease at the high end for all items/testlets except for CM442Q02, on which we impose the monotonicity constraints (Eq. 8). However, we often cannot distinguish the observed downward trend from a flat one due to large sampling variability, which is manifested by wider bootstrap confidence bands in those areas. For item CM603Q01 and testlet CM564, the downturn at the high end cannot be explained away by sampling variability. It implies that, among slow responders for the first nine items/testlets, the slower they respond to the first nine the faster they tend to response to the last two. The second observation concerns the dips in conditional mean functions when the latent slowness is between
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-1$$\end{document}
![]() and 0. Taking sampling variability into account, the dips are not substantial for CM603Q01 and CM564; also recall that the conditional mean function was forced to be non-decreasing for item CM442Q02. As such, the observed dips reflect a negative association between the above triplet and the remaining items/testlets for the subset of respondents whose latent slowness values fall slightly below average.
and 0. Taking sampling variability into account, the dips are not substantial for CM603Q01 and CM564; also recall that the conditional mean function was forced to be non-decreasing for item CM442Q02. As such, the observed dips reflect a negative association between the above triplet and the remaining items/testlets for the subset of respondents whose latent slowness values fall slightly below average.

Figure 3 Estimated conditional densities and means for log-10 response time (RT) variables (rescaled to [0, 1]). Each panel corresponds to a single item/testlet. Conditional densities of manifest variables given the slowness factor are visualized as contours in gray. Estimated conditional means are superimposed as solid curves in black. Dotted lines represent 90% bootstrap confidence bands (CBs) for estimated conditional mean curves.
Per a referee’s request, we also examine the relationship between item-level RT and the ability factor. In our simple structure model, the log-RT variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j = 1,\dots , m_1$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j = 1,\dots , m_1$$\end{document}
![]() , do not directly load on the ability factor
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}^*$$\end{document}
, do not directly load on the ability factor
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i2}^*$$\end{document}
![]() . Nevertheless, it remains possible to characterize the predictive distribution
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}|X_{i2}^*$$\end{document}
. Nevertheless, it remains possible to characterize the predictive distribution
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}|X_{i2}^*$$\end{document}
![]() by combining the conditional distribution of the slowness factor given the ability factor, i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}^*|X_{i2}^*$$\end{document}
by combining the conditional distribution of the slowness factor given the ability factor, i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1}^*|X_{i2}^*$$\end{document}
![]() , with the conditional distribution
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}|X_{i1}^*$$\end{document}
, with the conditional distribution
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij}|X_{i1}^*$$\end{document}
![]() (shown in Fig. 3). Such RT-ability associations turn out to be weak in the present data set; detailed results can be found in the supplementary document.
(shown in Fig. 3). Such RT-ability associations turn out to be weak in the present data set; detailed results can be found in the supplementary document.
Estimated item/testlet response functions are displayed in Fig. 4. Due to the large penalty weight (i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$10^{-1}$$\end{document}
![]() ), the fitted curves are smooth. For dichotomous items, the estimated curves for category 1 (i.e., correct answer) are largely in S-shape and typically have a restricted range (narrow than the entire interval [0, 1]). Similarly, estimated testlet response functions for the first and last categories also appear to have (often different) upper asymptotes. Some items, e.g., CM305Q01 and CM423Q01, are poorly discriminating, manifested by relatively flat IRFs.
), the fitted curves are smooth. For dichotomous items, the estimated curves for category 1 (i.e., correct answer) are largely in S-shape and typically have a restricted range (narrow than the entire interval [0, 1]). Similarly, estimated testlet response functions for the first and last categories also appear to have (often different) upper asymptotes. Some items, e.g., CM305Q01 and CM423Q01, are poorly discriminating, manifested by relatively flat IRFs.

Figure 4 Estimated conditional densities for discrete response variables, also known as item response functions (IRFs). Each panel corresponds to a single item/testlet. Curves for different categories are shown in different line types. Dotted lines represent 90% bootstrap confidence bands (CBs) for estimated IRFs.
4.3. Latent Density and Scores
A contour plot for the estimated two-dimensional LV density, which is computed from the estimated B-spline copula density with standard normal marginals (Eq. 13), is provided in the left panel of Fig. 5. It is observed that high ability respondents tend to response in a moderate speed, whereas low ability respondents can respond either very rapidly or very slowly. The shape of the density contours is nowhere near elliptical, which calls the standard practice of fitting a bivariate normal LV density into question. A better parameterization of the latent density for this data would be a mixture of two bivariate normals—one with a positive correlation for fast responders (i.e., slowness
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$<0$$\end{document}
![]() ) and the other with negative correlation for slow responders (i.e., slowness
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$>0$$\end{document}
) and the other with negative correlation for slow responders (i.e., slowness
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$>0$$\end{document}
![]() ). A similar pattern is observed when we plot the ability EAP scores against the slowness EAP scores (right panel of Fig. 5), with an exception that EAP scores tend to be less variable than the true LVs.
). A similar pattern is observed when we plot the ability EAP scores against the slowness EAP scores (right panel of Fig. 5), with an exception that EAP scores tend to be less variable than the true LVs.

Figure 5 Left: Estimated joint density for the slowness and ability factors (contours in gray) and the conditional mean of ability given slowness (black solid curve). Dotted lines represent 90% bootstrap confidence bands (CBs) for the estimated conditional mean curve. Right: Scatter plot for the expected a posteriori (EAP) scores of ability and slowness. A bivariate kernel density estimate (gray solid contours) and a smoothing spline regression line (black solid curve) are superimposed.
To better visualize the relationship between the two latent factors in the population, we also plot the conditional mean of ability given slowness (i.e., the black solid curve in the left panel of Fig. 5)—in other words, a nonlinear regression that predicts ability by slowness. The
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2$$\end{document}
![]() statistic (Eq. 31) of the population nonlinear regression is 0.45 with a 90% bootstrap CI [0.44, 0.47], indicating a strong association (Cohen, Reference Cohen1988, Chapter 9). Stated differently, knowing respondents’ processing speed on average reduces the uncertainty (measured by variance) in their mathematics ability by 45%. Recall that Zhan et al. (Reference Zhan, Liao and Bian2018) reported a correlation of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.2$$\end{document}
statistic (Eq. 31) of the population nonlinear regression is 0.45 with a 90% bootstrap CI [0.44, 0.47], indicating a strong association (Cohen, Reference Cohen1988, Chapter 9). Stated differently, knowing respondents’ processing speed on average reduces the uncertainty (measured by variance) in their mathematics ability by 45%. Recall that Zhan et al. (Reference Zhan, Liao and Bian2018) reported a correlation of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-0.2$$\end{document}
![]() between the speed (i.e., the reversal of slowness) and ability factors assuming bivariate normality, which implies
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2=(-0.2)^2 = 0.04$$\end{document}
between the speed (i.e., the reversal of slowness) and ability factors assuming bivariate normality, which implies
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2=(-0.2)^2 = 0.04$$\end{document}
![]() . The divergent conclusion reached by Zhan et al. (Reference Zhan, Liao and Bian2018) is likely attributed to the restrictive parameterization of their measurement model: They forced the LV density to be bivariate normal and thus failed to capture the nonlinear relationship. In addition, a smoothing spline regression fitted to the EAP scores (i.e., the black sold curve in the right panel of Fig. 5) suggests a similar predictive relationship: The observed multiple
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$R^2$$\end{document}
. The divergent conclusion reached by Zhan et al. (Reference Zhan, Liao and Bian2018) is likely attributed to the restrictive parameterization of their measurement model: They forced the LV density to be bivariate normal and thus failed to capture the nonlinear relationship. In addition, a smoothing spline regression fitted to the EAP scores (i.e., the black sold curve in the right panel of Fig. 5) suggests a similar predictive relationship: The observed multiple
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$R^2$$\end{document}
![]() statistic is 0.54, even higher than the population
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2$$\end{document}
statistic is 0.54, even higher than the population
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta ^2$$\end{document}
![]() .
.
As slowness/speed is a useful predictor of ability, it is anticipated that incorporating item-level RT information may improve the precision of IRT scale scores. Inspired by Bolsinova and Tijmstra (Reference Bolsinova and Tijmstra2018), we compare ability scores from the two-dimensional simple-structure model to those from the unidimensional semiparametric IRT model fitted to only responses in terms of their predictive precision (Sect. 2.5). It is first noted that the two sets of EAP scores are almost perfectly correlated (sample Pearson’s correlation > 0.99; see the left panel of Fig. 6). We then plot the predictive precisions associated with the two sets of EAP scores in the right panel of Fig. 5. Because the test is short and some items (e.g., items CM305Q01 and CM423Q01) have low discriminative power (manifested by flat item response functions), the predictive precisions are not high in general. Pooling across the entire sample, the mean predictive precision based on the unidimensional model is 4.68 with an interquartile range (IQR) [3.44, 5.71], and the median predictive precision based on the two-dimensional simple-structure model is 5.15 with an IQR [3.57, 6.45]. That is to say, using the two-dimensional model improves the predictive precision for ability scores by 10.1% on average.

Figure 6 Comparing expected a posteriori (EAP) scores for ability (left) and the associated predictive precisions (right) between the one-dimensional (1D) response-only model and the two-dimensional (2D) simple-structural model. In both panels, the dashed diagonal line in gray indicates equality.
To assess scoring precision at different slowness and ability levels, we split the sample into quintile groups by the slowness and ability EAP scores (from the two-dimensional model), respectively. A group-by-group summary of scoring precisions is provided in Table 3. When groups are formed by slowness scores, more increases in precision are typically observed in higher quintile groups; the percentage of improvement can be as high as 18.64% in the fifth quintile group. In contrast, the largest improvement is attained in the middle quintile group (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$15.89\%$$\end{document}
![]() ) when groups are determined by ability scores; the one-dimensional ability scores in the fifth quintile group are almost as precise as the two-dimensional scores.
) when groups are determined by ability scores; the one-dimensional ability scores in the fifth quintile group are almost as precise as the two-dimensional scores.
Table 3 Predictive precisions of ability scores in quintile groups.

Groups are determined by the slowness (left columns) and ability (right columns) scores computed from the two-dimensional simple-structure model.
Avg Prec: Average predictive precision within each group. 1D: One-dimensional model. 2D: Two-dimensional model.
5. Discussion
In the present paper, we perform a joint factor analysis for item response and RT data from the 2015 PISA mathematics assessment. In line with many previous studies that handled this type of data, our model features a simple factor structure with two LVs: The ability factor is indicated solely by item responses, the slowness factor is indicated solely by log-transformed RT variables, and the two LVs are permitted to covary in the population of respondents. The unique contribution of our work lies in the use of a semiparametric measurement model: We do not impose any restrictive functional forms of dependencies or distributional assumptions above and beyond the simple factor structure. Our model therefore fits the best to the data insofar as a simple factor structure is deemed proper. We approximate the functional parameters in the semiparametric factor model by cubic splines and estimate the resulting coefficients by PML: The penalty weights involved in the objective function are empirically selected via cross-validation. Inferences about model fit statistics and estimated functional parameters are conducted based on (nonparametric) bootstrap.
5.1. Implications
The semiparametric fitting reveals novel patterns that have yet been noticed in the existing literature, which has profound implications on the use of RT information in large-scale educational assessment.
First, a simple factor structure for ability and slowness fits reasonably well to the 2015 PISA mathematics data. Only two pairs of MVs exhibit excessive dependencies that are not well explained by the simple-structure model: Both pairs comprise the response and RT of the same item. Furthermore, including or excluding the RT variables of the two flagged pairs is inconsequential for model-based inferences. Our finding verifies the prevalent psychometric theory that between-person heterogeneity in item response behaviors are reflections of individual differences in ability and general processing speed. However, the existence of within-item local dependence between responses and RT, albeit not influential for the current analysis of the PISA data, should be reassessed in other applications of simple-structure factor models.
Second, commonly used parametric factor models are too simple to fully capture the MV-LV relations. Our semiparametric model implies that the conditional means of log-transformed RT variables are generally increasing but nonlinear functions of the slowness factor; the conditional variances appear to be non-constant for some items too. The most commonly used log-normal RT model, however, implies a linear conditional mean and a constant conditional variance and thus is evidently misspecified. As Liu and Wang (Reference Liu and Wang2022) also reported in that the log-normal RT model fits substantially worse than the semiparametric model in a different empirical example, cautions are advised in choose a suitable measurement model for item-level RT. Meanwhile, a large penalty weight is selected for the semiparametric IRT model, and consequently the fitted IRFs are smooth. While the shapes of the IRFs closely resemble logistic curves, the presence of lower and upper asymptotes hints at a 4PL model (Barton and Lord, Reference Barton and Lord1981), rather than the more popular 1PL and 2PL models in psychometric operations.
Third, the ability and slowness factors are strongly associated, which is probably the most surprising observation since a weak correlation was reported in Zhan et al.’s (Reference Zhan, Liao and Bian2018) analysis of the same data. The disparate finding of ours is ascribed to the use of a nonparametric latent density estimator, whereas the LV density is by default assumed to be (multivariate) normal in the vast majority of factor analysis applications. It then merely echoes a well-known fact that overly restrictive assumptions may lead to poorly fitting models and subsequently biased inferences. Diagnostics for non-normal LVs and measurement models equipped with non-parametric LV densities should be added to the routine toolbox for psychometricians. Future research is encouraged to examine the extent to which nonlinear factor models with non-normal latent densities can be beneficial in other assessment contexts.
Fourth, including item-level RT in the measurement model improves the precision of ability scores, which is an expected consequence as the ability factor can be well predicted by the slowness factor. While RT carries additional information about respondents’ ability, induced by the association between ability and general processing speed, it remains unclear whether RT should be officially used for scoring purposes in high-stake educational assessment. On the one hand, the joint factor model estimated in the present paper results in about 10% increase in predictive precisions for ability scores on average. Adaptive tests based on such a joint factor model may need fewer test items to reach the desired measurement precision, leading to more cost-effective test administrations. On the other hand, the same measurement model may no longer hold once the respondents are aware that response speed somehow affects their performance scores. In the latter case, a re-calibration of the joint factor model and a re-evaluation on the usefulness of RT information are necessary.
5.2. Limitations
There are also a number limitations to be addressed by future investigation.
First, the selection of penalty weights by multifold cross-validation is time consuming. A referee suggested that computing a one-sample estimate of cross-validation error (e.g., Akaike information criterion; AIC) or a large-sample approximation to the Bayesian marginal log-likelihood (e.g., Bayesian information criterion; BIC) is computationally advantageous. For nonparametric/semiparametric models using penalized smoothing splines, however, we must substitute a properly defined “effective degrees of freedom (edf)” for the number of parameters in the usual formulas of those information criteria. The ad hoc definition of edf proposed by Liu et al. (Reference Liu, Magnus and Thissen2016) for semiparametric IRT modeling can potentially be extended to the present context; however, the performance of the resulting information criteria in penalty weight selection remains unclear and should be investigated in future work.
Second, the sequential selection of multiple penalty weights does not guarantee that a globally optimal combination is found—it was only implemented as a workaround to alleviate the computational burden. Meanwhile, simultaneous selection on an outer-product grid (cf. Liu et al., Reference Liu, Magnus and Thissen2016) suffers from the “curse of dimensionality” and may be computationally inviable when the total number of penalty weights to be selected is large. Future research is encouraged to apply and evaluate optimization-based penalty weight selection, such as the “performance-oriented iteration” by Gu (Reference Gu1992), to semiparametric factor analysis. With the aid of optimization-based selection, it is also possible to explore the feasibility of selecting different penalty weights for different MVs, which further enhances the flexibility of the model.
Third, some of our decisions regarding locally dependent MVs can be refined. While coding each testlet response pattern as a unique category does not lead to any information loss, treating the summed RT within a testlet as a single MV does. In addition, we remove within-item local dependencies between responses and RT by simply excluding the RT variables. Although our treatments suffice for the purpose of the current analysis, it is natural to seek extensions of the proposed model to handle local dependencies in a more elegant way. In our opinion, the best strategy to approach a pair of locally dependent MVs is to directly model their bivariate conditional distribution given the LVs. For example, we may express the joint density of two log-RT variables, say
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij} = y$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij'} = z$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$Y_{ij'} = z$$\end{document}
![]() , given the latent slowness variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1} = x$$\end{document}
, given the latent slowness variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{i1} = x$$\end{document}
![]() using a logistic density transform with a three-way fANOVA decomposition (Gu, Reference Gu1995, Reference Gu2013):
using a logistic density transform with a three-way fANOVA decomposition (Gu, Reference Gu1995, Reference Gu2013):
Equation 34 involves six functional components, each of which can be approximated via basis expansion under suitable side conditions. Despite the straightforward formulation, simultaneous estimation of a large number of functional parameters proves to be computationally challenging.
Fourth, a referee made an important point that the residual correlation statistic (Eq. 25) only captures linear dependencies, which does not rule out the existence of nonlinear residual dependencies and is a major limitation of our diagnostic procedure. There exist various measures for nonlinear associations: Recent example include the Hellinger correlation (Geenens and Lafaye de Micheaux, Reference Geenens and Lafaye de Micheaux2022) and the Wasserstein dependence coefficient (Mordant & Segers, Reference Mordant and Segers2022; see also Chatterjee, Reference Chatterjee2022, for a review). However, those measures are often less intuitive to interpret as no common rules of thumb have been developed. As an alternative, one may fit an extended semiparametric factor model with bivariate conditional densities (Eq. 34) and identify nonlinear dependencies from graphical displays of estimated conditional densities.
Fifth, the proposed semiparametric factor model can be generalized in a number of ways. Sometimes, multiple latent constructs are simultaneously measured by an instrument (e.g., personality assessment); hence, a joint factor analysis of responses and RT for those measures involves at least three LVs. Such extensions of the current semiparametric simple-structure model suffers from a two-fold “curse of dimensionality”: The number of tensor-product basis functions grows exponentially when the dimension of a functional parameter’s domain increases, and the number of tensor-product quadrature points for likelihood approximation also increases exponentially as the dimension of LVs increases. While the EM algorithm with numerical quadrature can be replaced by stochastic approximation (Cai, Reference Cai2010a, Reference Caib; Gu and Kong, Reference Gu and Kong1998) to handle models with higher-dimensional LVs, reduced fANOVA parameterizations for conditional densities (Gu, Reference Gu1995, Reference Gu2013) and hierarchical formulations of B-spline copula (Kauermann et al., Reference Kauermann, Schellhase and Ruppert2013) are handy for constructing economical approximations of multivariate functional parameters.
Sixth, resampling based procedures (e.g., bootstrap) are time consuming even if parallel processing via OpenMP (Dagum and Menon, Reference Dagum and Menon1998) is enabled in the current implementation of PML estimation. For parametric models, inferential procedures based on large-sample approximations fares more computationally efficient. However, it is generally more difficult to prove large-sample results for semiparametric/nonparametric models as the functional parameters are infinite dimensional. Theoretical foundations on the asymptotic theory for semiparametric/nonparametric measurement models have yet been established and are left for future research.
Last but not least, we emphasize that semiparametric approaches are better suited for analyses that are exploratory and data-driven in nature. There are also scenarios in which confirmatory and theory-driven model building is preferred: For instance, when the test is designed based on cognitive theory and administered in a controlled laboratory setting (e.g., the well known “mental rotation” example in the RT literature; Borst et al., Reference Borst, Kievit, Thompson and Kosslyn2011). One prominent example of theory-driven psychometrics is the integration of diffusion decision models with factor analysis (e.g., Kang et al., Reference Kang, Boeck and Ratcliff2022, Reference Kang, Jeon and Partchev2023a,Reference Kang, Molenaar and Ratcliffb). Data-driven semiparametric models and theory-driven parametric models are both important yet mutually distinct tools to advance psychometricians’ understanding in the role of processing speed in test-taking behavior.
Funding
The work is sponsored by the National Science Foundation under grant No. 1826535.
Declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
The dataset analyzed during the current study is available in the OECD PISA Database (https://www.oecd.org/pisa/data/).















