Relations between conditional probabilities, revisions of probabilities in the light of new information, and conditions of ideal rationality are discussed herein. The formal character of conditional probabilities, and their significance for epistemic states of agents is taken up. Then principles are considered that would, under certain conditions, equate rationally revised probabilities on new information with probabilities reached by conditionalizing on this information. And lastly the possibility of kinds of ‘books’ against known non-conditionalizers is explored, and the question is taken up, What, if anything, would be wrong with a person against whom such a book could be made?
1. The standard mathematical treatment takes probability functions as basic, and conditional probabilities defined. If P(-) is a probability function, then 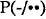 is its conditional probability function if and only if P(h/e) is defined only for e such that P(e) > 0, and is then equal to P(e & h)/P(e).
is its conditional probability function if and only if P(h/e) is defined only for e such that P(e) > 0, and is then equal to P(e & h)/P(e).