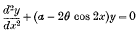Proceedings of the Royal Society of Edinburgh, Volume 52 - 1933
- This volume was published under a former title. See this journal's title history.
Proceedings
XXI.—Relative Co-ordinates
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 345-353
-
- Article
- Export citation
XXII.—Tables of the Elliptic-cylinder Functions
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 355-423
-
- Article
- Export citation
XXIII.—Zeros and Turning Points of the Elliptic-cylinder Functions
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 424-433
-
- Article
- Export citation
XXIV.—Adrenaline and the Œstrous Cycle in the Mouse
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 434-444
-
- Article
- Export citation
Obituary Notices
Alexander G. Burgess, MA., D.Sc.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 445-446
-
- Article
-
- You have access
- Export citation
James Edward Crombie, M.A., LL.D.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 447-448
-
- Article
-
- You have access
- Export citation
Robert W. Dron, M.A., M.Inst.C.E., M.Inst.M.E.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 449-450
-
- Article
-
- You have access
- Export citation
Giulio Fano, 1856-1932
-
- Published online by Cambridge University Press:
- 15 September 2014, p. 451
-
- Article
-
- You have access
- Export citation
Sir Patrick Geddes
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 452-454
-
- Article
-
- You have access
- Export citation
Eugène Gley (1857-1930)
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 455-457
-
- Article
-
- You have access
- Export citation
William Gordon, B.Sc. (Eng.), Ph.D., M.I.Mech.E.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 458-459
-
- Article
-
- You have access
- Export citation
John Walter Gregory, D.Sc., LL.D., F.R.S.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 460-462
-
- Article
-
- You have access
- Export citation
Alexander James, M.D., F.R.C.P.Ed.
-
- Published online by Cambridge University Press:
- 15 September 2014, p. 463
-
- Article
-
- You have access
- Export citation
Malcolm Laurie, B.A., D.Sc., F.L.S.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 464-465
-
- Article
-
- You have access
- Export citation
Graham Lusk, 1866-1932
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 466-467
-
- Article
-
- You have access
- Export citation
The Very Rev. Dugald Mackichan, M.A., D.D., LL.D.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 468-469
-
- Article
-
- You have access
- Export citation
Mr James Malloch, M.A.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 470-471
-
- Article
-
- You have access
- Export citation
Emeritus Professor David Henry Marshall, M.A.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 472-473
-
- Article
-
- You have access
- Export citation
Alexander Philip, M.A., LL.B. (Edin.)
-
- Published online by Cambridge University Press:
- 15 September 2014, p. 474
-
- Article
-
- You have access
- Export citation
Col. Sir Bruce Gordon Seton
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 475-476
-
- Article
-
- You have access
- Export citation