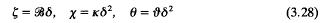Index
Index to Volume 104
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. i-ii
-
- Article
- Export citation
Research Article
Left approximate identities in algebras of compact operators on Banach spaces
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 169-175
-
- Article
- Export citation
Correction
Corrigendum: Bifurcations near a multiple eigenvalue of the rectangular plate problem
-
- Published online by Cambridge University Press:
- 14 November 2011, p. 177
-
- Article
- Export citation
Front matter
PRM volume 104 issue 3-4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 104 issue 3-4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Front matter
PRM volume 104 issue 1-2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 104 issue 1-2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 (
(