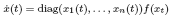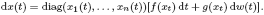Research Article
Continuous families of exponential attractors for singularly perturbed equations with memory
-
- Published online by Cambridge University Press:
- 30 March 2010, pp. 329-366
-
- Article
- Export citation
Weakly compact operators and the strong* topology for a Banach space
-
- Published online by Cambridge University Press:
- 08 December 2010, pp. 1249-1267
-
- Article
- Export citation
Large-time behaviour of solutions to non-Newtonian filtration equations with nonlinear boundary sources
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 833-855
-
- Article
- Export citation
The domain of analyticity of Dirichlet–Neumann operators
-
- Published online by Cambridge University Press:
- 30 March 2010, pp. 367-389
-
- Article
- Export citation
Regularity for subquadratic parabolic systems: higher integrability and dimension estimates
-
- Published online by Cambridge University Press:
- 08 December 2010, pp. 1269-1308
-
- Article
- Export citation
Multiple positive solutions for singular elliptic equations with weighted Hardy terms and critical Sobolev–Hardy exponents
-
- Published online by Cambridge University Press:
- 21 May 2010, pp. 617-633
-
- Article
- Export citation
On travelling wavefronts of Nicholson's blowflies equation with diffusion
-
- Published online by Cambridge University Press:
- 04 February 2010, pp. 135-152
-
- Article
- Export citation
Dynamics of a non-local delayed reaction–diffusion equation without quasi-monotonicity
-
- Published online by Cambridge University Press:
- 01 October 2010, pp. 1081-1109
-
- Article
- Export citation
Unbounded delay stochastic functional Kolmogorov-type system
-
- Published online by Cambridge University Press:
- 08 December 2010, pp. 1309-1334
-
- Article
- Export citation
Quasi-completely continuous multilinear operators
-
- Published online by Cambridge University Press:
- 21 May 2010, pp. 635-649
-
- Article
- Export citation
Auslander's condition and tilting theory
-
- Published online by Cambridge University Press:
- 01 October 2010, pp. 1111-1118
-
- Article
- Export citation
A quasilinear problem without the Ambrosetti–Rabinowitz-type condition
-
- Published online by Cambridge University Press:
- 30 March 2010, pp. 391-398
-
- Article
- Export citation
Geometric Langlands duality and the equations of Nahm and Bogomolny
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 857-895
-
- Article
- Export citation
Stabilization and a class of functionals for linear parabolic control systems
-
- Published online by Cambridge University Press:
- 04 February 2010, pp. 153-174
-
- Article
- Export citation
Contents List to Volume
Index to Volume 140
-
- Published online by Cambridge University Press:
- 08 December 2010, pp. 1337-1341
-
- Article
- Export citation
Research Article
Projections of surfaces in the hyperbolic space along horocycles
-
- Published online by Cambridge University Press:
- 30 March 2010, pp. 399-418
-
- Article
- Export citation
The asymptotic Teichmüller space and the asymptotic Grunsky map
-
- Published online by Cambridge University Press:
- 21 May 2010, pp. 651-672
-
- Article
- Export citation
Hardy operators on weighted amalgams
-
- Published online by Cambridge University Press:
- 04 February 2010, pp. 175-188
-
- Article
- Export citation
Asymptotic behaviour, uniqueness and stability of coexistence states of a non-cooperative reaction–diffusion model of nuclear reactors
-
- Published online by Cambridge University Press:
- 04 February 2010, pp. 189-201
-
- Article
- Export citation
On boundary variational–hemivariational inequalities of elliptic type
-
- Published online by Cambridge University Press:
- 30 March 2010, pp. 419-434
-
- Article
- Export citation

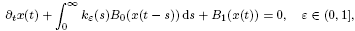
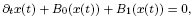
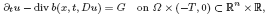
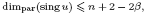
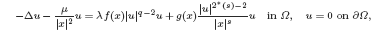
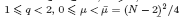 , 0 ≤
, 0 ≤ 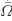 , that change sign on Ω.
, that change sign on Ω.