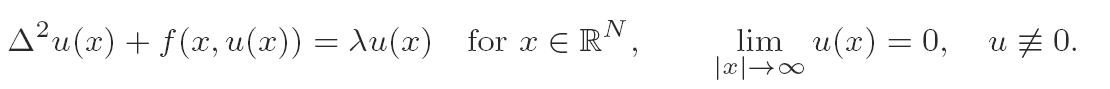Research Article
An operator is a product of two quasi-nilpotent operators if and only if it is not semi-Fredholm
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 935-944
-
- Article
- Export citation
Continuous invertibility of minimal Sturm–Liouville operators in Lebesgue spaces
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 53-70
-
- Article
- Export citation
Decaying positive solutions to a system of nonlinear elliptic equations
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 301-320
-
- Article
- Export citation
On composition and absolute-valued algebras
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 717-731
-
- Article
- Export citation
About a Liouville comparison principle for entire weak solutions of quasilinear elliptic partial differential inequalities
-
- Published online by Cambridge University Press:
- 30 July 2007, pp. 547-557
-
- Article
- Export citation
Generic affine differential geometry of curves in Rn
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1195-1205
-
- Article
- Export citation
On the quasi-nodal map for the Sturm–Liouville problem
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 71-86
-
- Article
- Export citation
A lower semi-continuity result for polyconvex functionals in SBV
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 321-336
-
- Article
- Export citation
Multiple solutions of nonlinear Schrödinger equations via flow invariance and Morse theory
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 945-969
-
- Article
- Export citation
Branches of solutions to semilinear biharmonic equations on RN
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 733-758
-
- Article
- Export citation
Entire solutions of reaction—diffusion equations with balanced bistable nonlinearities
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1207-1237
-
- Article
- Export citation
The implicit function theorem and multi-bump solutions of periodic partial differential equations
-
- Published online by Cambridge University Press:
- 30 July 2007, pp. 559-583
-
- Article
- Export citation
Non-local homogenized limits for composite media with highly anisotropic periodic fibres
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 87-114
-
- Article
- Export citation
Wave pinning in strips
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 971-995
-
- Article
- Export citation
Asymptotic behaviour of positive steady states to a predator—prey model
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 759-778
-
- Article
- Export citation
On the structure of the Whittaker sublocus of the moduli space of algebraic curves
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 337-346
-
- Article
- Export citation
Existence of minimizers for a finite-strain micromorphic elastic solid
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 997-1012
-
- Article
- Export citation
Single-valued conjugates and holomorphic extendibility
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 347-350
-
- Article
- Export citation
On uniqueness for a class of nonlinear boundary-value problems
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 779-784
-
- Article
- Export citation
Integral and S-factorizable multilinear mappings
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 115-137
-
- Article
- Export citation