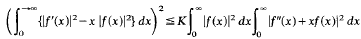Research Article
On an inequality of Hardy-Littlewood type: I
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 131-140
-
- Article
- Export citation
The existence of infinitely many bifurcating branches
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 307-320
-
- Article
- Export citation
Uniform operator σ-additivity of indefinite integrals induced by scalar-type spectral operators
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 141-146
-
- Article
- Export citation
Global a priori estimates for a viscous reactive gas*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 321-333
-
- Article
- Export citation
A note on the paper “Existence conditions for eigenvalue problems generated by compact multiparameter operators” by P. Binding, P. J. Browne and L. Turyn
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 147-148
-
- Article
- Export citation
Hopf bifurcation at multiple eigenvalues with zero eigenvalue
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 335-352
-
- Article
- Export citation
Nondassical eigenvalue distribution of one-dimensional Schrödinger operators
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 149-158
-
- Article
- Export citation
On Malcev algebras in which all subideals are ideals
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 353-363
-
- Article
- Export citation
Front matter
PRM volume 101 issue 3-4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
On a discrete-time version of a problem of A. J. Pritchard and J. Zabczyk
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 159-161
-
- Article
- Export citation
Symmetry sets
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 163-186
-
- Article
- Export citation
Back matter
PRM volume 101 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Front Matter
PRM volume 101 issue 1-2 Cover and Front Matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
- Export citation
Back Matter
PRM volume 101 issue 1-2 Cover and Back Matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
- Export citation