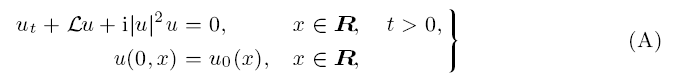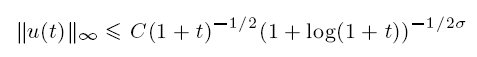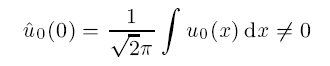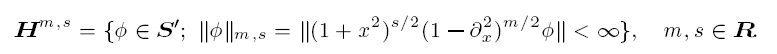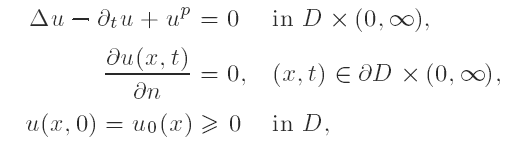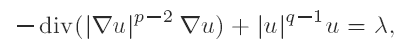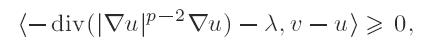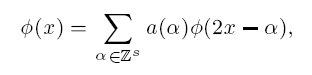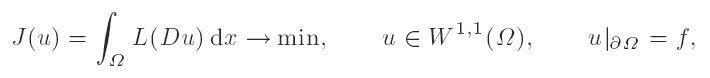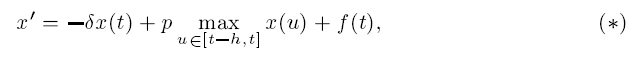Research Article
Large-time behaviour of solutions to the dissipative nonlinear Schrödinger equation
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1029-1043
-
- Article
- Export citation
Existence of topological multivortex solutions in the self-dual gauge theories
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1293-1309
-
- Article
- Export citation
Steady vortex in a uniform shear flow of an ideal fluid
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 801-812
-
- Article
- Export citation
The critical Fujita number for a semilinear heat equation in exterior domains with homogeneous Neumann boundary values
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 591-602
-
- Article
- Export citation
Ergodic properties and Weyl M-functions for random linear Hamiltonian systems
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1045-1079
-
- Article
- Export citation
Positive solutions for a class of nonlinear elliptic problems in RN
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 141-166
-
- Article
- Export citation
A construction of laminates from rank-1 polygons
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1311-1335
-
- Article
- Export citation
Phragmen–Lindelöf theorems and the asymptotic behaviour of solutions of quasilinear elliptic equations in slabs
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 335-373
-
- Article
- Export citation
Non-existence of solutions for some nonlinear elliptic equations involving measures
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 167-187
-
- Article
- Export citation
Rings graded by bisimple inverse semigroups
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 603-609
-
- Article
- Export citation
One-sided extrapolation at infinity and singular integrals
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1081-1102
-
- Article
- Export citation
The LSW model for Ostwald ripening with kinetic undercooling
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1337-1361
-
- Article
- Export citation
C*-convex sets and completely bounded bimodule homomorphisms
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 375-387
-
- Article
- Export citation
Local linear independence of refinable vectors of functions
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 813-826
-
- Article
- Export citation
Characterization of homogeneous scalar variational problems solvable for all boundary data
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 611-631
-
- Article
- Export citation
Quasiconvexity is not invariant under transposition
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 389-395
-
- Article
- Export citation
Stability and existence of multiple periodic solutions for a quasilinear differential equation with maxima
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1103-1118
-
- Article
- Export citation
Existence of geodesics in static Lorentzian manifolds with convex boundary
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 189-215
-
- Article
- Export citation
Asymptotic properties of the solutions to stochastic KPP equations
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1363-1381
-
- Article
- Export citation
The initial value problem for the non-homogeneous Navier—Stokes equations with general slip boundary condition
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 827-835
-
- Article
- Export citation