Article contents
XV.—Dual Series Relations* II. Dual Relations Involving Dini Series
Published online by Cambridge University Press: 14 February 2012
Synopsis
The problem discussed is that of determining the sequence {an} such that
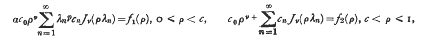
where (λn) is the sequence of positive zeros of the function λJν(λ) + HJν(λ), arranged in order of increasing magnitude, þ, ν and H are real constants (−I <þ < I, ν > −½) and f1(ρ), f2(ρ) are prescribed. By expressing the sequence {cn} in terms of a sequence of integrals involving a function g(t) the problem is reduced to the solution of a non-singular Fredholm integral of the second kind for g(t).
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 66 , Issue 3 , 1963 , pp. 161 - 172
- Copyright
- Copyright © Royal Society of Edinburgh 1963
References
References to Literature
Erdélyi, A. (Ed.), 1954. Tables of Integral Transforms. New York, London: McGraw-Hill.Google Scholar
Sneddon, I. N., 1962. “Fractional Integration and Dual Integral Equations.” N. C. St. Coll. Appl. Math. Res. Group Rep., PSR-6.CrossRefGoogle Scholar
Sneddon, I. N., and Srivastav, R. P., 1964. “Dual Series Relations—I. Dual Relations involving Fourier-Bessel Series.” Proc. Roy. Soc. Edin., A, 66, 150–160.Google Scholar
Watson, G. N., 1944. A Treatise on the Theory of Bessel Functions, 2nd Edn. Cambridge University Press.Google Scholar
- 4
- Cited by


