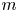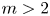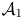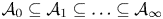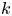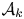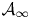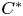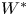Weakly concave operators

Abstract

We study a class of left-invertible operators which we call weakly concave operators. It includes the class of concave operators and some subclasses of expansive strict $m$-isometries with $m > 2$. We prove a Wold-type decomposition for weakly concave operators. We also obtain a Berger–Shaw-type theorem for analytic finitely cyclic weakly concave operators. The proofs of these results rely heavily on a spectral dichotomy for left-invertible operators. It provides a fairly close relationship, written in terms of the reciprocal automorphism of the Riemann sphere, between the spectra of a left-invertible operator and any of its left inverses. We further place the class of weakly concave operators, as the term $\mathcal {A}_1$, in the chain $\mathcal {A}_0 \subseteq \mathcal {A}_1 \subseteq \ldots \subseteq \mathcal {A}_{\infty }$ of collections of left-invertible operators. We show that most of the aforementioned results can be proved for members of these classes. Subtleties arise depending on whether the index $k$ of the class $\mathcal {A}_k$ is finite or not. In particular, a Berger–Shaw-type theorem fails to be true for members of $\mathcal {A}_{\infty }$. This discrepancy is better revealed in the context of $C^*$- and $W^*$-algebras.

1. Introduction

We denote by $\mathbb {Z}_+,$ $\mathbb {Z}$ and $\mathbb {R}$ the sets of non-negative integers, integers and real numbers, respectively. We write $\varOmega ^{*}$ for the set $\{\bar {z} \colon z \in \varOmega \}$ whenever $\varOmega$ is a subset of the complex plane $\mathbb {C}$. For a positive real number $r,$ $\mathbb {D}_r$ stands for the open disc $\{z \in \mathbb {C} \colon |z| < r\}.$ Set $\mathbb {D} := \mathbb {D}_1.$ For positive real numbers $r$ and $R$ with $r < R$, we denote by $\mathbb {A}(r, R)$ the annulus $\{z \in \mathbb {C} \colon r < |z| < R\}$. We write $\mathbb {R}[x]$ for the ring of polynomials in one real variable $x$ with real coefficients.

Unless otherwise stated, all Hilbert spaces appearing below are complex. Let $\mathcal {H}$ denote a Hilbert space and let $\mathcal {B}(\mathcal {H})$ stand for the unital $C^*$-algebra of bounded linear operators on $\mathcal {H}$ with the identity operator $I$ as the unit. Denote by $[S,T]$ the commutator $ST-TS$ of $S,T \in \mathcal {B}(\mathcal {H}).$ The commutator $[S^*, S]$ is called the self-commutator of $S$. We write $\ker T$, ${\mathcal {R}}(T)$ and $|T|$ for the kernel, the range and the modulus of an operator $T \in \mathcal {B}(\mathcal {H}).$ The spectrum, the approximate point spectrum and the spectral radius of $T$ are denoted by $\sigma (T)$, $\sigma _{ap}(T)$ and $r(T)$, respectively.

An operator $T$ in $\mathcal {B}(\mathcal {H})$ is left-invertible if there exists $L \in \mathcal {B}(\mathcal {H})$ (a left-inverse of $T$) such that $LT=I.$ Note that $T$ is left-invertible if and only if $0\notin \sigma _{ap}(T)$, or equivalently if and only if $T^*T$ is invertible (as a member of $\mathcal {B}(\mathcal {H})$). Following [35], we call the operator $T':=T(T^*T)^{-1}$ the Cauchy dual of $T$ whenever $T$ is left-invertible. For notational brevity, we write $T^{\prime n}$ instead of $(T^{\prime })^n,$ the $n$th power of $T^{\prime }$, when $n$ is a non-negative integer (in general, $T^{\prime n}$ does not coincide with $T^{n\prime }:= (T^n)^{\prime }$). The Cauchy dual operator provides a canonical choice of a left-inverse $L:=T'^*$ for any left-invertible operator $T.$ We refer the reader to [35] for the role that the Cauchy dual operator plays in the solution of the wandering subspace problem for the Bergman shift. Recall that an operator $T \in \mathcal {B}(\mathcal {H})$ has the wandering subspace property if

\[ \mathcal{H} = \bigvee_{n \in \mathbb{Z}_+} T^n(\ker T^*). \]

We call $T$ analytic if $\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^n) =\{0\}.$ Clearly, an analytic operator on a non-zero Hilbert space is never invertible. We say that $T$ is concave if

\[ I-2T^*T+T^{*2}T^{2} \leqslant 0. \]

The class of concave operators was introduced by Richter [31] on the occasion of investigating invariant subspaces of the Dirichlet shift. The importance of concave operators was emphasized by Richter, who proved that analytic concave operators have the wandering subspace property (see [31, Theorem 1]). In turn, Shimorin proved that concave operators have Wold-type decomposition (see [35, Theorem 3.6(A)]). In this paper, we generalize the notion of a concave operator, preserving some of their important properties (see § 3 and 7 for the motivation). The first step generalization refers to weakly concave operators.

Definition 1.1 A left-invertible operator $T \in \mathcal {B}(\mathcal {H})$ is said to be weakly concave if it satisfies the following conditions:

(1.1)\begin{align} \sigma_{ap}(T) & \subseteq \partial\mathbb{D}, \end{align}

(1.2)\begin{align} \|x\| & \leqslant \|Tx\|, \quad x \in \mathcal{H}, \end{align}

(1.3)\begin{align} \|T^*x\|' & \leqslant \|Tx\|', \quad x \in \mathcal{H}, \end{align}

where $\|\cdot \|'$ is the norm on $\mathcal {H}$ given by $\|x\|':=\|T'x\|$ for $x \in \mathcal {H}$ and $T'$ denotes the Cauchy dual of $T$.

Remark 1.2 In view of [26, Lemma 3.1] and the inclusion $\partial \sigma (T) \subseteq \sigma _{ap}(T)$ (see [17, Proposition VII.6.7]), it is easy to see that, under the assumption (1.2), the condition (1.1) is equivalent to $\sigma (T) \subseteq \overline {\mathbb {D}}$ (and to $r(T) \leqslant 1$). $\diamondsuit$

The following theorem, which is one of the main results of this paper, generalizes [35, Theorem 3.6(A)].

Theorem 1.3 Suppose that $T \in \mathcal {B}(\mathcal {H})$ is a weakly concave operator. Let $\mathcal {H}_u$ and $\mathcal {H}'_u$ denote the closed vector subspaces of $\mathcal {H}$ given by

(1.4)\begin{equation} \mathcal{H}_u :=\bigcap_{n=0}^{\infty}{\mathcal{R}}(T^n)\quad and \quad \mathcal{H}'_u := \bigcap_{n=0}^{\infty}{\mathcal{R}}(T'^n). \end{equation}

Then $\mathcal {H}'_u \subseteq \mathcal {H}_u$ and $\mathcal {H}'_u$ reduces $T.$ Moreover,

(1.5)\begin{equation} T = U \oplus S\ \text{with respect to the decomposition}\ \mathcal{H} = \mathcal{H}'_u \oplus (\mathcal{H}'_u)^{{\perp}}, \end{equation}

where $U \in \mathcal {B}(\mathcal {H}'_u)$ is unitary and $S \in \mathcal {B}((\mathcal {H}'_u)^{\perp })$ has the wandering subspace property.

In general, the Wold-type decomposition obtained in Theorem 1.3 is weaker than Shimorin's one in the sense that the operator $S$ in the decomposition (1.5) of $T$ may not be analytic. However, in the case where $T$ is concave, it can be seen that $\mathcal {H}'_u=\mathcal {H}_u,$ which allows us to recover [35, Theorem 3.6(A)] (see Corollary 6.1). The proof of Theorem 1.3 is based on the circle of ideas developed by Shimorin in [35] together with the spectral dichotomy principle, which is given in § 5.

We also prove the following Berger–Shaw-type theorem together with the Carey–Pincus trace formula for analytic finitely cyclic weakly concave operators (cf. [18, Theorem 2.1, p. 152] and [12, Proposition 2.21]). Recall that $T\in {\mathcal {B}}(\mathcal {H})$ is finitely cyclic if there is a finite dimensional vector subspace $\mathcal {M}$ of $\mathcal {H}$, called a cyclic space of $T$, such that $\mathcal {H} = \bigvee _{n \in \mathbb {Z}_+} T^n (\mathcal {M}).$

Theorem 1.4 Suppose that $T \in \mathcal {B}(\mathcal {H})$ is an analytic finitely cyclic weakly concave operator. Then $T$ and $T'$ have trace class self-commutators. Moreover, for any complex polynomials $p, q$ in two complex variables $z$ and $\bar z$,

\begin{align*} \mathrm{tr}\,[p(T', T'^*), q(T', T'^*)] & = \mathrm{tr}\,[p(T, T^*), q(T, T^*)] \\ & = \frac{1}{\pi} \dim \ker T^* \int_{\mathbb{D}} \left(\frac{\partial p}{\partial \bar z}\frac{\partial q}{\partial z} -\frac{\partial p}{\partial z}\frac{\partial q}{\partial \bar z}\right) (z, \bar z)\,dA(z), \end{align*}

where $dA$ denotes the Lebesgue planar measure.

The proofs of Theorems 1.3 and 1.4 will be given in § 6.

Remark 1.5 Let $T$ be as in Theorem 1.4. Then, in particular, we have

\[ \mathrm{tr}\,[T'^*, T'] =\mathrm{tr}\,[T^*, T] = \dim \ker T^*. \]

Further, the Pincus principal function of $T'$ is equal to $-\dim \ker T^*$ times the characteristic function of the open unit disk [see (6.9)]. The reader is referred to [11] for the definition of the Pincus principal function. $\diamondsuit$

The paper is organized as follows. In § 3, we discuss basic properties of weakly concave operators, including their relation to the theory of hyponormal operators. In § 4, we provide examples of $3$-isometric weakly concave operators which are not concave (see Example 4.5). In § 5, we establish the spectral dichotomy principle for left-invertible operators (see Theorem 5.1). This principle is a key component of the proofs of Theorems 1.3 and 1.4 (see § 6). Both theorems are generalized in Theorems 7.2 and 7.4 to the case of operators of class $\mathcal {A}_k$, where $k\in \mathbb {Z}_+ \cup \{\infty \}$ (see Definition 7.1). If the underlying Hilbert space is infinite dimensional, then the class $\mathcal {A}_0$ is larger than the class of concave operators, the class $\mathcal {A}_1$ consists precisely of weakly concave operators and the sequence $\{\mathcal {A}_k\}_{k=0}^{\infty }$ is strictly increasing (see Example 7.6). In § 8, we present necessary and sufficient conditions for some restrictions of the Cauchy dual operator of a left-invertible operator to be hyponormal (see Propositions 8.2 and 8.7). Section 9 is devoted to $C^*$- and $W^*$-algebraic analogues of the classes $\mathcal {A}_k.$

2. Preliminaries

The left spectrum $\sigma _l(T)$ of $T \in \mathcal {B}(\mathcal {H})$ is defined as the set of those $\lambda$ in $\mathbb {C}$ for which $T-\lambda I$ is not left-invertible. Similarly, one can define the right spectrum $\sigma _r(T)$ of $T.$ It is easy to see that

\[ \sigma_l(T)=\sigma_{ap}(T)= (\sigma_r(T^*))^*. \]

We say that an operator $T \in \mathcal {B}(\mathcal {H})$ with closed range is left Fredholm (resp. right Fredholm) if $\dim \ker T< \infty$ (resp. $\dim \ker T^* < \infty$). Operators which are simultaneously left and right Fredholm are called Fredholm operators. The essential spectrum $\sigma _e(T)$ of $T$ is the complement of the set of those $\lambda \in \mathbb {C}$ for which $T-\lambda I$ is Fredholm. The function $\text {ind}_T$ defined by

\[ \text{ind}_T(\lambda)\,:=\,\dim \ker(T-\lambda I)-\dim \ker (T^*-\bar{\lambda} I), \quad \lambda \in \mathbb{C} {\setminus} \sigma_e(T), \]

is called the Fredholm index of $T$. Similarly, we define the left essential spectrum $\sigma _{le}(T)$ and the right essential spectrum $\sigma _{re}(T)$ of $T.$ We refer the reader to [17] for the foundations of the theory of Fredholm operators.

An operator $T$ in ${\mathcal {B}}(\mathcal {H})$ is of trace class if $\|T\|_{1, \mathcal {E}}:= \sum _{n =0}^{\infty }\langle {|T|e_n},\,{e_n} \rangle$ is finite for every choice of an orthonormal basis $\mathcal {E}=\{e_n\}_{n \in \mathbb {Z}_+}$ of $\mathcal {H}.$ The number $\|T\|_{1, \mathcal {E}}$ turns out to be independent of the choice of an orthonormal basis $\mathcal {E}$ of $\mathcal {H}$ and is denoted by $\|T\|_1.$ It is called the trace norm of $T.$ In case $T$ is of trace class, the trace of $T$ given by $\text {tr}(T) =\sum _{n = 0}^{\infty }\langle {Te_n},\,{e_n} \rangle$ is a finite number. Again, it is independent of the choice of an orthonormal basis $\mathcal {E}$ of $\mathcal {H}$ (see [39] for more details on trace class operators).

An operator $T\in \mathcal {B}(\mathcal {H})$ is said to be completely non-unitary (resp., completely non-normal) if there is no nonzero closed subspace of $\mathcal {H}$ reducing $T$ to a unitary (resp., normal) operator. Clearly, if $T \in \mathcal {B}(\mathcal {H})$ is analytic, then $T$ is completely non-unitary. The following fact is easy to verify.

(2.1)\begin{equation} \textit{If }\ T\in \mathcal{B}(\mathcal{H})\ has\ the\ wandering\ subspace\ property, then\ T\ is\ completely\ \textit{non-unitary}. \end{equation}

An operator $T \in \mathcal {B}(\mathcal {H})$ is said to be hyponormal if the self-commutator of $T$ is positive. The reader is referred to [18, Chapter IV] and [28, Chapter 1] for the fundamentals of the theory of hyponormal operators including the statements of Berger–Shaw Theorem and Putnam's inequality. Given a positive integer $m$ and $T \in \mathcal {B}(\mathcal {H})$, we set

\[ B_m(T) = \sum_{k=0}^m ({-}1)^k {m \choose k}{T^*}^kT^k. \]

We say that $T$ is a contraction (resp. an expansion) if $B_1(T) \geqslant 0$ (resp., ${B_1(T)\leqslant 0}$). For an integer $m \geqslant 2$, an operator $T \in \mathcal {B}(\mathcal {H})$ is said to be an $m$-isometry if ${B_m(T) = 0}$. By a strict $m$-isometry, we understand an $m$-isometry which is not an $(m-1)$-isometry (or not an isometry if $m=2$). It is well known that any concave operator is expansive (see [31, Lemma 1]). Furthermore, the approximate point spectrum of any $m$-isometry and any concave operator is contained in the unit circle $\partial \mathbb {D}$ (see [3, Lemma 1.21], [26, Lemma 3.1] and [31, Lemma 1]). In particular, the Cauchy dual operator of an $m$-isometry or a concave operator is well defined.

Straightforward computations yield the following properties of the Cauchy dual operator, where in general $P_{\mathcal {M}}$ denotes the orthogonal projection of $\mathcal {H}$ onto a closed vector subspace $\mathcal {M}$ of $\mathcal {H}$.

Proposition 2.1 If $T\in \mathcal {B}(\mathcal {H})$ is left-invertible and $T=U|T|$ is the polar decomposition of $T$, then

1. (i) $U=T|T|^{-1}$ and $|T'|=|T|^{-1},$

2. (ii) $T'= U|T'|$ is the polar decomposition of $T'$,

3. (iii) $P_{{\mathcal {R}}(T)} = T'T^* = UU^*$.

3. An invitation to weakly concave operators

As mentioned in Introduction, any concave operator admits a Wold-type decomposition (see [35, Theorem 3.6]). Since concave $m$-isometries are necessarily $2$-isometries (see [14, Proposition 4.9]), the above result is insufficient to obtain a Wold-type decomposition for concave strict $m$-isometries if $m > 2.$ As a first step towards obtaining the Wold-type decomposition for expansive $m$-isometries, we consider a class of operators containing concave operators and some strict $m$-isometries with $m> 2.$ Furthermore, in view of the fact that the Cauchy dual of an expansive $m$-isometry is not necessarily hyponormal (in contrast to the case of concave operators, see [36, p. 294] or [12, Theorem 2.9]), it is natural to search for a class of left-invertible operators satisfying a hyponormality-like condition. This motivated us to define the notion of weak concavity (see Definition 1.1), which is central to the present article.

According to [31, Lemma 1] and Remark 1.2, concave operators satisfy the conditions (1.1) and (1.2). Hence, trying to generalize the concept of concavity, we included them in Definition 1.1. Although at first glance it is unclear why we use the term ‘weakly concave’, the following theorem sheds more light on this by connecting, via Cauchy dual, the theory of weakly concave operators with the theory of hyponormal operators.

Proposition 3.1 Let $T \in \mathcal {B}(\mathcal {H})$ be a left-invertible operator. Then the following conditions are equivalent:

1. (i) $T$ satisfies (1.3),

2. (ii) $T(T^*T)^{-1}T^* \leqslant T^*(T^*T)^{-1}T,$

3. (iii) $P_{{\mathcal {R}}(T)} \leqslant T^*(T^*T)^{-1}T,$

4. (iv) the restriction of $T'$ to its range is hyponormal.

In particular, any concave operator is weakly concave.

Proof. That the conditions (i)–(iii) are equivalent is immediate from the following identities (see Proposition 2.1):

(3.1)\begin{equation} T'^*T' = (T^*T)^{{-}1}\quad \text{and}\quad T^{\prime}T^*= P_{{\mathcal{R}}(T)}. \end{equation}

To see that the conditions (i) and (iv) are equivalent, note that $T'|_{{\mathcal {R}}(T')}$ is hyponormal if and only if

\[ \|(T'|_{{\mathcal{R}}(T')})^*T'x\| \leqslant \|T'^2x\|,\quad x \in \mathcal{H}. \]

Using (3.1) and the equalities $(T'|_{{\mathcal {R}}(T')})^* = P_{{\mathcal {R}}(T')}T'^*|_{{\mathcal {R}}(T')}$ and ${\mathcal {R}}(T')={\mathcal {R}}(T)$, we conclude that the operator $T'|_{{\mathcal {R}}(T')}$ is hyponormal if and only if

\[ \|T'T^*x\| \leqslant \|T'Tx\|, \quad x \in \mathcal{H}. \]

The above inequality coincides with (1.3). This shows that the conditions (i)–(iv) are equivalent.

To show the remaining part, recall that any concave operator satisfies (1.1) and (1.2). Since the Cauchy dual of a concave operator is hyponormal (see [36, p. 294]) and the restriction of a hyponormal operator to its closed invariant subspace is hyponormal (see [18, Proposition II.4.4]), an application of the implication (iv)$\Rightarrow$(i) completes the proof.

Our next goal is to show that the only invertible weakly concave operators are unitary operators (cf. Corollary 3.3). In fact, this is a consequence of a much more general fact proved below.

Proposition 3.2 Let $T \in \mathcal {B}(\mathcal {H})$ satisfy (1.1) and let $T'|_{\mathcal {H}_u'}$ be hyponormal, where $\mathcal {H}_u':=\bigcap _{n=0}^{\infty } {\mathcal {R}}(T^{\prime n})$. Then the following statements are valid:

1. (i) $T$ is unitary if $T$ is invertible,

2. (ii) $T$ is completely non-normal if $T$ is analytic.

Proof. (i) Assume that $T$ is invertible. Since $\partial \sigma (T) \subseteq \sigma _{ap}(T)$, we infer from (1.1) that $\sigma (T) \subseteq \partial \mathbb {D}$. Hence

(3.2)\begin{equation} \sigma(T^*) = \sigma(T)^* \subseteq\partial \mathbb{D}. \end{equation}

Noting that the invertibility of $T$ implies the invertibility of $T'$, we deduce that ${\mathcal {H}_u'=\mathcal {H}}$. From the assumption that $T'|_{\mathcal {H}_u'}$ is hyponormal, we see that $T'$ is hyponormal. However, by invertibility of $T$, $T'=T^{*-1},$ which by [18, Proposition II.4.4] implies that $T^*$ is hyponormal. Hence, by (3.2) and the second corollary on [40, Pg 473], $T$ is unitary.

(ii) Assume now that $T$ is analytic. Suppose to the contrary that $T$ has a non-zero normal direct summand, say $N$. Then by (1.1), we have

\[ \sigma(N) = \sigma_{ap}(N) \subseteq \sigma_{ap}(T) \subseteq\partial \mathbb{D}. \]

Hence, $N$ is unitary. This contradicts the fact that every analytic operator is completely non-unitary.

The following corollary is immediate from Propositions 3.1 and 3.2 and [18, Proposition II.4.4].

Corollary 3.3 If $T \in \mathcal {B}(\mathcal {H})$ is weakly concave, then the following statements are valid:

1. (i) $T$ is unitary if $T$ is invertible,

2. (ii) $T$ is completely non-normal if $T$ is analytic.

4. Examples

In this section, we show that there are weakly concave operators which are not concave (see Example 4.5 below). This is done by means of unilateral weighted shifts. Recall that for a bounded sequence $\{w_n\}_{n = 0}^{\infty }$ of positive real numbers, there exists a unique operator $W\in \mathcal {B}(\ell ^2)$ (called a unilateral weighted shift with weight sequence $\{w_n\}_{n = 0}^{\infty }$) such that

\[ We_n \mathrel{\mathop :}= w_n e_{n + 1}, \quad n \in \mathbb{Z}_+, \]

where $\{e_n\}_{n = 0}^{\infty }$ stands for the standard orthonormal basis of $\ell ^2,$ the Hilbert space of square summable complex sequences indexed by $\mathbb {Z}_+.$ Note that unilateral weighted shifts are always analytic. Before providing the aforementioned example, we need some auxiliary results. We begin by characterizing those unilateral weighted shifts whose given power is left-invertible and satisfies the condition (1.3).

Proposition 4.1 Let $W$ be a unilateral weighted shift with weight sequence $\{w_n\}_{n=0}^{\infty }$ and let $k$ be a positive integer. Then the following statements are equivalent:

1. (i) $W^k$ is left-invertible and satisfies (1.3),

2. (ii) $\inf _{{n \in \mathbb {Z}_+}}w_{n} > 0$ and $\prod _{j=0}^{k-1} \frac {w_{n+j}}{w_{k+n+j}} \geqslant 1$ for every integer $n \geqslant k.$

Proof. First, observe that if $T\in \mathcal {B}(\mathcal {H}),$ then for any positive integer $m$, $T$ is left-invertible if and only if $T^m$ is left-invertible. Hence, $W^k$ is left-invertible if and only if $\inf _{n \in \mathbb {Z}_+} w_n > 0$. This means that there is no loss of generality in assuming that all powers of $W$ are left-invertible. Noting that

\begin{align*} W^k e_n & = \left(\prod_{j=0}^{k-1} w_{n+j}\right) e_{k+n}, \quad n \in \mathbb{Z}_+, \\ W^{*k} e_{k+n} & = \left(\prod_{j=0}^{k-1} w_{n+j}\right) e_{n}, \quad n \in \mathbb{Z}_+, \end{align*}

we deduce that

(4.1)\begin{equation} W^{*k}(W^{*k}W^k)^{{-}1}W^k e_n =\prod_{j=0}^{k-1} \frac{w_{n+j}^2}{w_{k+n+j}^2} e_{n}, \quad n \in \mathbb{Z}_+. \end{equation}

Clearly

(4.2)\begin{equation} P_{{\mathcal{R}}(W^k)} e_n =\begin{cases} 0 & \text{if } n=0, \ldots, k-1, \\ e_n & \text{if } n \geqslant k. \end{cases} \end{equation}

Combining (4.1) and (4.2) with the equivalence (i) $\Leftrightarrow$ (iii) of Proposition 3.1 completes the proof.

The next result we need is closely related to [4, Proposition 2.3]. It can be deduced from [6, Lemma 3.1] by applying the fact that the (entry-wise) product of Hausdorff moment sequences is a Hausdorff moment sequence (see [7, p. 179]; see also [7, § 6.2.4] for the definition of the Hausdorff moment sequence) and by using the fundamental theorem of algebra (see [23, Theorem V.3.19]).

Proposition 4.2 Suppose that $p$ is a polynomial in one real variable which has only negative real roots and whose leading coefficient is positive. Then $p(n) > 0$ for all $n\in \mathbb {Z}_+$ and $\{1/p(n)\}_{n=0}^{\infty }$ is a Hausdorff moment sequence.

The following characterization of weakly concave $m$-isometric unilateral weighted shifts is of independent interest.

Proposition 4.3 Suppose that $W$ is a unilateral weighted shift with weight sequence $\{w_n\}_{n = 0}^{\infty }$ and $m \geqslant 2$. Then the following statements are equivalent:

1. (i) $W$ is a weakly concave $m$-isometry,

2. (ii) there exists a polynomial $p\in \mathbb {R}[x]$ of degree at most $m-1$ such that

   (4.3)\begin{align} p(n) > 0\ and\ w^2_n =\frac{p(n+1)}{p(n)}\ for\ all\ n \in \mathbb{Z}_+, \end{align}
   (4.4)\begin{align} p(n) \leqslant p(n+1)\ for\ all\ n \in \mathbb{Z}_+, \end{align}
   (4.5)\begin{align} p(n)p(n+2) \leqslant p(n+1)^2\ for\ all\ n \in \mathbb{Z}_+\backslash \{0\}. \end{align}

Moreover, if $p$ is as in Proposition 4.2, then (4.4) and (4.5) hold.

Proof. By [1, Theorem 2.1] (see also [25, Proposition A.2] and [8, Theorem 3.4]), $W$ is an $m$-isometry if and only if there exists a polynomial $p\in \mathbb {R}[x]$ of degree at most $m-1$ such that (4.3) is valid. Therefore, there is no loss of generality in assuming that $W$ is an $m$-isometry with $p\in \mathbb {R}[x]$ of degree at most $m-1$ that satisfies (4.3). By [3, Lemma 1.21], $W$ satisfies (1.1). Hence $0\notin \sigma _{ap}(W)$, or equivalently $W$ is left-invertible. Moreover, $W$ is an expansion if and only if $w_n \geqslant 1$ for every $n \in \mathbb {Z}_+$, or equivalently if and only if (4.4) holds. Hence, applying (4.3) and Proposition 4.1 with $k=1$, we see that the statements (i) and (ii) are equivalent (the condition (4.5) corresponds to (1.3)).

Finally, if $p$ is as in Proposition 4.2, then $\{1/p(n)\}_{n=0}^{\infty }$ is a Hausdorff moment sequence which as such is monotonically decreasing and logarithmically convex [the former is equivalent to (4.4), while the latter implies (4.5)].

We also need the following fact, which was proved for finite systems of operators in [14]. For the reader's convenience, we give its short proof below. This result is a generalization of [38, Proposition 3.6(ii)].

Proposition 4.4 [14, Proposition 4.9]

Suppose that $T \in \mathcal {B}(\mathcal {H})$ is a concave $m$-isometry for some $m\geqslant 2$. Then $T$ is a $2$-isometry.

Proof. It follows from [31, Lemma 1(b)] that

(4.6)\begin{equation} \|T^n h\|^2 \leqslant \|h\|^2 + n (\|Th\|^2 - \|h\|^2), \quad h \in \mathcal{H}, \, n\in \mathbb{Z}_+. \end{equation}

By [3, p. 389] (see also [25, Theorem 3.3]), for every $h \in \mathcal {H}$ the expression $\|T^n h\|^2$ is a polynomial in¹ $n$ of degree at most $m-1$. Combined with (4.6), this implies that $m \leqslant 2$, which completes the proof.

We are now ready to construct a class of analytic strict $3$-isometric weakly concave operators. Note that such operators cannot be concave which is immediate from Proposition 4.4.

Example 4.5 Let $p\in \mathbb {R}[x]$ be the polynomial defined by $p(x)=|x+z|^2$ for $x\in \mathbb {R}$, where $z=u+iv \in \mathbb {C}$ with $u, v \in \mathbb {R}$ such that $v \neq 0$. Since $p$ is of degree $2$ and $p(n) > 0$ for all $n\in \mathbb {Z}_+$, the unilateral weighted shift $W$ with weight sequence $\{w_n\}_{n = 0}^{\infty }$ defined by (4.3) is a $3$-isometry (see [1, Theorem 2.1] and [25, Proposition A.2]). Note that

(4.7)\begin{equation} p\ \textit{satisfies } (4.4)\ \Longleftrightarrow\ u \geqslant -\frac{1}{2}. \end{equation}

Straightforward computations show that

\[ p\ \textit{satisfies}\ (4.5) \iff \forall n\geqslant 1 \colon 2((n+u)^2-v^2) + 4(n+u) + 1 \geqslant 0. \]

Combined with (4.7) and Proposition 4.3, this implies that $W$ is weakly concave if and only if

(4.8)\begin{equation} u \geqslant -\frac{1}{2}\ {\rm and}\ 2((1+u)^2-v^2) + 4(1+u) + 1 \geqslant 0. \end{equation}

Since the second inequality in (4.8) is equivalent to

\[ 2v^2 \leqslant 2(1+u)^2 + 4(1+u)+1, \]

we deduce that if $u \geqslant 0$ and $v^2 \leqslant 7/2$, then $W$ is weakly concave.

Assume now that $u \geqslant -\frac {1}{2}.$ Although, in view of (4.8), $W$ need not be weakly concave, quite surprisingly, $W^k$ turns out to be weakly concave for sufficiently large $k$. To see this, we can argue as follows. By (4.7), $W$ is expansive. Since $W$ is a 3-isometry, it follows from [24, Theorem 2.3] that for every integer $k\geqslant 1,$ $W^k$ is an expansive $3$-isometry, and so by [3, Lemma 1.21], $T = W^k$ satisfies (1.1) and (1.2). Observe that the second inequality in the condition (ii) of Proposition 4.1 holds if and only if

(4.9)\begin{equation} p(n)p(n+2k) \leqslant p(n+k)^2, \quad n \geqslant k. \end{equation}

Straightforward computations show that

\[ p\ \textit{satisfies } (4.9)\ \iff \forall n\geqslant k \colon 2((n+u)^2-v^2) + 4(n+u)k + k^2 \geqslant 0. \]

Now if $k$ is any positive integer such that $k^2 \geqslant 2v^2,$ then the above inequality holds, and so $p$ satisfies (4.9). Summarizing, if $u\geqslant -\frac {1}{2}$ and $k \geqslant \sqrt {2}|v|$, then by Proposition 4.1, $W^k$ is a weakly concave $3$-isometry. Note that if $k$ is any positive integer, then $W^k$ is not a $2$-isometry. This follows from [25, Theorem 3.3] by observing that the identity

\[ \|(W^k)^n e_0\|^2 \mathop =\limits^{(4.3)}\frac{p(kn)}{p(0)} = \frac{(kn+u)^2 + v^2}{u^2 + v^2}, \quad n\in \mathbb{Z}_+, \]

implies that the expression $\|(W^k)^n e_0\|^2$ is a polynomial in $n$ of degree $2$ (see footnote ¹). Hence, by Proposition 4.4, $W^k$ is not concave for any positive integer $k$. $\diamondsuit$

5. A spectral dichotomy

Recall the well-known fact that the spectra of an invertible operator $T \in \mathcal {B}(\mathcal {H})$ and its inverse $T^{-1} \in \mathcal {B}(\mathcal {H})$ are related to each other and the correspondence is given by

(5.1)\begin{equation} \sigma(T^{{-}1})=\phi(\sigma(T)), \end{equation}

where $\phi (\lambda )=1/\lambda$ is an automorphism of the punctured plane $\mathbb {C}_{\bullet }:=\mathbb {C} \backslash \{0\}$ (see [39, Theorem 2.3.2] for the general version of the spectral mapping theorem). A question worth considering in the context of the present paper is to find the counterpart of this simple fact for left-invertible operators $T$. More specifically, if $L$ is a left-inverse of $T$, then what is the relationship between the spectra of $T$ and $L$. The purpose of this section is largely to answer this question. It is worth noting that among the left inverses of a left-invertible operator $T$ there exist such as $T^{\prime *}$, where $T^{\prime }$ is the Cauchy dual of $T$ (see [30, Proposition 5.1] for concrete examples).

Before stating the main result of this section, observe that if $T\in \mathcal {B}(\mathcal {H})$ is left-invertible and $L\in \mathcal {B}(\mathcal {H})$ is a left-inverse of $T$, then

(5.2)\begin{equation} 0\in \sigma(T)\ {\rm if\ and\ only\ if}\ 0\in \sigma(L). \end{equation}

Theorem 5.1 [Spectral dichotomy]

Let $T \in \mathcal {B}(\mathcal {H})$ be a left-invertible operator with a left-inverse $L \in \mathcal {B}(\mathcal {H})$. Consider the automorphism $\phi$ of the punctured plane $\mathbb {C}_{\bullet }$ given by $\phi (z) = 1/{z}$ for $z \in \mathbb {C}_{\bullet },$ and extend it to the Riemann sphere $\mathbb {C} \cup \{\infty \}$ by setting $\phi (0)=\infty$ and $\phi (\infty )=0.$ Then

(5.3)\begin{equation} either\ \mathbb{C} {\setminus}\phi(\sigma_{l}(L))\subseteq\sigma_{r}(T){\setminus} \sigma_{l}(T)\ or\ \phi(\sigma(L)) =\sigma(T) \end{equation}

according as $0 \in \sigma (T)$ or $0 \notin \sigma (T)$ $($ see Fig. 1$)$. In any case, $0 \notin \partial \sigma (L)$ and

(5.4)\begin{equation} \phi(\partial \sigma(L)) \subseteq \sigma_r(T). \end{equation}

FIG. 1. The relationship between the spectra of a left-invertible operator $T$ and its left-inverse $L,$ where ${}^\centerdot$ denotes the origin in the complex plane.

Proof. We begin by noting that

(5.5)\begin{equation} L-\lambda I = L (I-\lambda T) ={-}\lambda L(T-\lambda^{{-}1}I), \quad \lambda \in \mathbb{C}_{{\bullet}}. \end{equation}

Second, there is no loss of generality in assuming that $0\in \sigma (T)$ (because otherwise $L=T^{-1}$, and so we can use (5.1) to get $\phi (\sigma (L)) =\sigma (T)$). Thus, by (5.2), $L$ is not invertible. Since $T$ is left-invertible, $T$ is not right-invertible. In turn, because $L$ is right-invertible, $L$ is not left-invertible. This yields

(5.6)\begin{equation} 0 \in \sigma_r(T) {\setminus} \sigma_l(T)\quad\text{and}\quad 0 \in \sigma_l(L) {\setminus} \sigma_r(L). \end{equation}

We claim that

(5.7)\begin{equation} \phi(\mathbb{C}_{{\bullet}} {\setminus}\sigma_{l}(L)) \subseteq \sigma_{r}(T){\setminus} \sigma_{l}(T). \end{equation}

For, assume that $\lambda \in \mathbb {C}_{\bullet } {\setminus} \sigma _{l}(L)$. Then there exists $L_1\in \mathcal {B}(\mathcal {H})$ such that

(5.8)\begin{equation} L_1(L-\lambda I)=I. \end{equation}

Hence, by (5.5), $T-\lambda ^{-1}I$ is left-invertible, meaning that $\lambda ^{-1}\in \mathbb {C} {\setminus} \sigma _{l}(T)$. Thus, to get (5.7), it suffices to show that $\lambda ^{-1} \in \sigma _{r}(T).$ Suppose, to the contrary, that $\lambda ^{-1} \in \mathbb {C}{\setminus} \sigma _{r}(T)$. As a consequence, $T-\lambda ^{-1}I$ is invertible. Right-multiplying (5.5) by the inverse of $T-\lambda ^{-1}I$ yields

(5.9)\begin{equation} (L-\lambda I) (T-\lambda^{{-}1}I)^{{-}1} ={-} \lambda L. \end{equation}

Now left-multiplying (5.9) by $L_1$ leads to

(5.10)\begin{equation} (T - \lambda^{{-}1} I)^{{-}1}\mathop =\limits^{(5.8)} L_1(L-\lambda I)(T - \lambda^{{-}1}I)^{{-}1} ={-} \lambda L_1 L. \end{equation}

Finally, left-multiplying (5.10) by $T - \lambda ^{-1} I$ gives

\[ I = \left(-\lambda (T - \lambda^{{-}1} I) L_1\right) L. \]

This means that $L$ is left-invertible, showing that $0 \in \mathbb {C} \backslash \sigma _{l}(L)$, which contradicts (5.6). This justifies (5.7). Combined with (5.6), this implies the first inclusion in (5.3).

To prove (5.4), we first check that $0 \notin \partial \sigma (L)$. Note that

(5.11)\begin{equation} 0 \in \partial \sigma(L) \Longleftrightarrow 0 \in \partial \sigma(L^*). \end{equation}

Next, since $L$ is right-invertible and

\[ \sigma_{ap}(L^*)=\sigma_{l}(L^*)=\sigma_{r}(L)^{*}, \]

we see that $0 \notin \sigma _{ap}(L^*)$. Combined with (5.11) and $\partial \sigma (L^*) \subseteq \sigma _{ap}(L^*),$ this implies that $0 \notin \partial \sigma (L)$. Since, by (5.7), $\phi (\mathbb {C}_{\bullet } {\setminus} \sigma (L)) \subseteq \sigma _{r}(T) {\setminus} \sigma _{l}(T),$ and the right spectrum of any bounded linear operator is closed, the inclusion $\phi (\partial \sigma (L)) \subseteq \sigma _r(T)$ now follows from the continuity of $\phi.$ This completes the proof.

Corollary 5.2 Let $T \in \mathcal {B}(\mathcal {H})$ be a left-invertible operator with a left-inverse $L \in \mathcal {B}(\mathcal {H})$. Then the spectral radius $r(L)$ of $L$ is positive and

(5.12)\begin{equation} either\ {\mathbb{D}}_{1/r(L)} \subseteq\sigma_r(T) {\setminus} \sigma_l(T)\ or\ \sigma(T) \subseteq \mathbb{C} {\setminus} {\mathbb{D}}_{1/r(L)} \end{equation}

according to $0 \in \sigma (T)$ or $0 \notin \sigma (T)$. In particular, $r(T)r(L) \geqslant 1.$

Proof. By Theorem 5.1, $0 \notin \partial \sigma (L)$ and so $r(L) > 0$. According to the definition of the spectral radius, $\mathbb {D}_{1/r(L)} \cap \phi (\sigma (L)) = \emptyset$, and thus the desired dichotomy is immediate from Theorem 5.1. The inequality $r(T)r(L) \geqslant 1$ follows from (5.12).

Remark 5.3 Since $L^nT^n=I$ holds for any positive integer $n,$ one may derive $r(T)r(L) \geqslant 1$ also from the Gelfand spectral radius formula. $\diamondsuit$

Note that if $T\in \mathcal {B}(\mathcal {H})$ is a left-invertible operator, then by Theorem 5.1 applied to the left-inverse $L=T^{\prime *}$ of $T$, we get

(5.13)\begin{equation} \mathbb{C} {\setminus} \phi(\sigma_l(T^{\prime *})) \subseteq \sigma_r(T) {\setminus} \sigma_l(T)\ provided\ 0 \in \sigma(T). \end{equation}

In general, the above inclusion is strict. We discuss this in more detail in the context of unilateral weighted shifts. Before that, we introduce the necessary notation. For $T \in \mathcal {B}(\mathcal {H})$, we set $i(T):= \lim _{n \to \infty } (\inf _{\|x\|=1}\|T^nx\|)^{1/n}.$ Clearly, $i(T) \leqslant r(T)$. Moreover, by [37, Proposition 13], we have

\[ \sigma_{ap}(T) \subseteq \{\lambda \in\mathbb{C} \colon i(T) \leqslant |\lambda| \leqslant r(T)\}. \]

Example 5.4 Let $W\in \mathcal {B}(\ell ^2)$ be a left-invertible unilateral weighted shift with positive weights $\{w_n\}_{n=0}^{\infty }$. Then $W',$ the Cauchy dual of $W,$ is a left-invertible unilateral weighted shift with weights $\{w_n^{-1}\}_{n=0}^{\infty }$. As a consequence of [32, Theorem 6] and [37, Theorem 4], we get

(5.14)\begin{equation} \sigma_r(W)=\sigma(W) = \overline{\mathbb{D}}_{r(W)}\ {\rm and}\ \sigma_r(W^{\prime})=\sigma(W^{\prime}) =\overline{\mathbb{D}}_{r(W^{\prime})}. \end{equation}

In turn, [32, Theorem 1] implies that $\sigma _l(W)=\overline {\mathbb {A}(i(W), r(W))}$. Since

\[ \sigma_l(W^{\prime *}) = \sigma_r(W^{\prime})^*\mathop =\limits^{(5.14)} \overline{\mathbb{D}}_{r(W^{\prime})}, \]

and $0\in \sigma (W)$, we deduce from (5.14) that the condition (5.13) takes the following form

\[ \mathbb{D}_{\frac{1}{r(W^{\prime})}} = \mathbb{C}{\setminus} \phi\big(\overline{\mathbb{D}}_{r(W^{\prime})}\big) = \mathbb{C} {\setminus} \phi(\sigma_l(W^{\prime *})) \subseteq\sigma_r(W) {\setminus} \sigma_l(W) = \mathbb{D}_{i(W)}. \]

If we assume that equality holds in the above inclusion, then $\frac {1}{r(W^{\prime })}=i(W),$ which is not true in general (see e.g., [15, Example 2], where $r(W^{\prime })= 2$ and $i(W) \geqslant 2^{-3/4}$). $\diamondsuit$

We conclude this section with some applications of Theorem 5.1 to the theory of Cauchy dual operators.

Corollary 5.5 Let $T \in \mathcal {B}(\mathcal {H})$ be a left-invertible operator such that $0 \in \sigma (T)$ and let $T'$ be the Cauchy dual of $T.$ Then the following assertions hold:

1. (i) if $\sigma _r(T') \subseteq \overline {\mathbb {D}},$ then ${\mathbb {D}} \subseteq \sigma _r(T){\setminus} \sigma _l(T),$

2. (ii) if $T$ is a contraction such that $\sigma _r(T')\subseteq \overline {\mathbb {D}}$, then $\sigma _r(T)=\sigma (T)=\overline {\mathbb {D}}$.

Proof. (i) Suppose that $\sigma _r(T') \subseteq \overline {\mathbb {D}}$. Set $L=T^{\prime *}$. Then $L$ is a left-inverse of $T$ and

\[ \sigma_l(L) = \sigma_l(T^{\prime *}) =\sigma_r(T^{\prime})^* \subseteq \overline{\mathbb{D}}. \]

This combined with Theorem 5.1 yields

\[ \mathbb{D}=\mathbb{C} {\setminus}\phi(\overline{\mathbb{D}}) \subseteq \mathbb{C} {\setminus} \phi(\sigma_l(L)) \subseteq\sigma_r(T) {\setminus} \sigma_l(T), \]

which justifies (i).

(ii) Assume now that $\|T\| \leqslant 1$ and $\sigma _r(T') \subseteq \overline {\mathbb {D}}$. Then using (i) and the well-known fact that the spectral radius of a bounded linear operator is at most its operator norm, we get

\[ {\mathbb{D}} \subseteq \sigma_r(T) {\setminus}\sigma_l(T) \subseteq \sigma_r(T) \subseteq \sigma(T) \subseteq \overline{{\mathbb{D}}}. \]

Since $\sigma _r(T)$ and $\sigma (T)$ are closed subsets of $\mathbb {C}$, the proof is complete.

Remark 5.6 It is well known and easy to prove that the Cauchy dual $T'$ of $T$ is left-invertible and $(T')'=T.$ This together with (5.2) implies that $0 \in \sigma (T)$ if and only if $0 \in \sigma (T').$ In particular, the roles of $T$ and $T'$ in Corollary 5.5 can be interchanged. $\diamondsuit$

A solution of the wandering subspace problem for concave operators given by Richter in [31] can also be obtained from the computations of the spectra of the Cauchy dual operators (see [12, Lemma 2.14]). In turn, these computations can be derived from the Bunce result (see [18, Chapter II, $\S$12]) on the existence of a rich supply of non-zero $*$-homomorphisms of the $C^*$-algebra generated by a hyponormal operator (see the proof of [12, Lemma 2.14]). Interestingly, the following fact, which plays an important role in the proofs of Theorems 1.3 and 1.4, and which generalizes [12, Lemma 2.14(ii)], can be deduced from the spectral dichotomy.

Corollary 5.7 Let $T \in {\mathcal {B}}(\mathcal {H})$ be a non-invertible expansion such that $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$ and let $T'$ be the Cauchy dual of $T.$ Then

1. (i) $\sigma (T) = \overline {\mathbb {D}} = \sigma (T')$,

2. (ii) $\sigma _{ap}(T) = \partial {\mathbb {D}} =\sigma _{ap}(T')$.

Proof. Recall the fact that for Hilbert space operators, left spectrum and approximate point spectrum coincide. Note that $T'$ is a contraction because $T$ is an expansion. Further, since $T$ is not invertible, $T'$ is not invertible. Also, because the boundary of the spectrum is contained in the approximate point spectrum and $0 \in \sigma (T),$ we infer from $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$ that $\sigma (T) = \overline {\mathbb {D}}$ and $\sigma _{ap}(T)=\partial \mathbb {D}.$ By applying Corollary 5.5(ii) to $T'$, we obtain $\sigma (T')=\overline {\mathbb {D}}$ and $\partial \mathbb {D} \subseteq \sigma _{ap}(T')$ (see Remark 5.6). An application of Corollary 5.5(i) to $T'$ yields

\[ \mathbb{D} \subseteq \sigma(T') {\setminus}\sigma_l(T') = \overline{\mathbb{D}} {\setminus} \sigma_{ap}(T') \subseteq \mathbb{D}, \]

and hence $\sigma _{ap}(T')=\partial \mathbb {D}$. This completes the proof.

6. Proofs of Theorems 1.3 and 1.4

The proof of Theorem 1.3 is based on a technique developed in [35].

Proof of Theorem 1.3 In view of Corollary 3.3(i), we may assume that $0 \in \sigma (T).$ Since the subspace $\mathcal {H}'_u$ [see (1.4)] is invariant for $T'$, we can consider the operator $R:=T'|_{\mathcal {H}'_u} \in \mathcal {B} (\mathcal {H}'_u).$ Note that $T'$ is bounded from below and $R$ maps $\mathcal {H}'_u$ onto $\mathcal {H}'_u$, hence $R$ is invertible. By Corollary 5.7(ii), we have

(6.1)\begin{equation} \sigma_{ap}(R) \subseteq \sigma_{ap}(T') =\partial \mathbb{D}. \end{equation}

Since $0 \notin \sigma (R)$ and $\partial \sigma (R) \subseteq \sigma _{ap}(R)$, we deduce from (6.1) that $\sigma (R) \subseteq \partial \mathbb {D}.$ Further, by Proposition 3.1, $R$ being a restriction of the hyponormal operator $T'|_{{\mathcal {R}}(T')}$ to $\mathcal {H}'_u$ is hyponormal. Hence, by [40, second corollary, p. 473], $R$ is unitary. Recall that if $\mathcal {M}$ is a closed invariant subspace for a contraction $A \in \mathcal {B}(\mathcal {H})$ such that $A|_{\mathcal {M}}$ is unitary, then $\mathcal {M}$ reduces $A$ (see e.g., [13, Lemma 2.5]). Applying this fact to $A=T'$ ($T'$ is a contraction because $T$ is an expansion) and $\mathcal {M}=\mathcal {H}'_u,$ we deduce that $\mathcal {H}'_u$ reduces $T'$. By [6, Proposition 2.2] applied to $T^{\prime }$, $\mathcal {H}'_u$ reduces $T$ and $T|_{\mathcal {H}'_u} = R^{\prime }$. Consequently, $T|_{\mathcal {H}'_u}$ is unitary and so $T(\mathcal {H}'_u)=\mathcal {H}'_u.$ This in turn implies that $\mathcal {H}'_u \subseteq \mathcal {H}_u$ (see (1.4)). On the other hand, by [35, Proposition 2.7(i)] we have

\[ (\mathcal{H}'_u)^{{\perp}}=\bigvee_{n \in \mathbb{Z}_+} T^n(\ker T^*). \]

Since $T|_{\mathcal {H}'_u}$ is unitary, we conclude that $T|_{\mathcal {H} \ominus \mathcal {H}'_u}$ has the wandering subspace property. This completes the proof.

Corollary 6.1 [35, Theorem 3.6(A)]

If $T \in \mathcal {B}(\mathcal {H})$ is a concave operator, then $T$ has the Wold-type decomposition, that is, $\mathcal {H}_{u}$ reduces $T$, $T|_{\mathcal {H}_{u}}$ is unitary and

\[ \mathcal{H} = \mathcal{H}_{u} \oplus \bigvee_{n\in \mathbb{Z}_+} T^n(\ker T^*), \]

where $\mathcal {H}_u$ is as in (1.4).

Proof. It follows from [35, Proposition 3.4] that $\mathcal {H}_u$ reduces $T$ to a unitary operator, so by (2.1) and Theorem 1.3 we conclude that $\mathcal {H}_u = \mathcal {H}'_u$, which completes the proof.

Corollary 6.2 Any weakly concave operator $T \in \mathcal {B}(\mathcal {H})$ which is analytic has the Wold-type decomposition.

Before proving the next lemma needed in the proof of Theorem 1.4, we state the following fact (see [22, Proposition 1(i)] and [5, Lemma 3.6]).

(6.2)\begin{equation} \textit{If }\ T \in \mathcal{B}(\mathcal{H})\ is\ finitely\ cyclic, then\ \ker(T^*-\lambda I)\ is\ finite\ dimensional\ for\ every\ \lambda \in \mathbb{C}. \end{equation}

Lemma 6.3 Suppose that $T \in \mathcal {B}(\mathcal {H})$ is a finitely cyclic operator. Then

(6.3)\begin{align} \sigma_{e}(T) & \subseteq \sigma_{ap}(T), \end{align}

(6.4)\begin{align} \mathrm{ind}_{T}(\lambda) & ={-} \dim \ker (T^*-\bar \lambda I), \quad \lambda\in \mathbb{C}{\setminus} \sigma_{ap}(T). \end{align}

Proof. Suppose that $\lambda \in \mathbb {C} {\setminus} \sigma _{ap}(T)$. Then $T-\lambda I$ is left-invertible, so the space ${\mathcal {R}}(T-\lambda I)$ is closed and $\dim \ker (T-\lambda I)=0$. According to (6.2), $\dim \ker (T^*-\bar \lambda I)< \infty$. This means that the operator $T-\lambda I$ is Fredholm, so $\lambda \in \mathbb {C}{\setminus} \sigma _{e}(T).$ This proves (6.3). Moreover, we have

\begin{align*} \mathrm{ind}_{T}(\lambda)& = \dim \ker (T-\lambda I) - \dim \ker (T^*-\bar \lambda I) \\ & ={-} \dim \ker (T^*-\bar \lambda I). \end{align*}

This completes the proof.

Proof of Theorem 1.4 By (6.2), $\ker T^*$ is finite dimensional. Combined with [35, Proposition 2.7(ii)] and the hypothesis that $T$ is analytic, this implies that $T'$ is finitely cyclic with the cyclic space $\ker T^*$. Moreover, since the range of $T'$ is closed, we have

(6.5)\begin{equation} \bigvee_{n \in \mathbb{Z}_+} (T'|_{{\mathcal{R}}(T')})^n\big(T'(\ker T^*)\big) = T' \Big(\bigvee_{n \in \mathbb{Z}_+} T'^n(\ker T^*)\Big) ={\mathcal{R}}(T'). \end{equation}

It follows that $T'|_{{\mathcal {R}}(T')}$ is finitely cyclic with the cyclic space $T'(\ker T^*)$. By Proposition 3.1, $T'|_{{\mathcal {R}}(T')}$ is hyponormal. Hence, by the Berger–Shaw Theorem (see [18, Theorem IV.2.1]), $T'|_{{\mathcal {R}}(T')}$ has a trace class self-commutator. Since $T'$ is a finite rank perturbation of $T'|_{{\mathcal {R}}(T')} \oplus 0$, where $0$ is the zero operator on $\ker {T^{\prime *}} = \ker {T^*}$, and the set of finite rank operators is a $*$-ideal, one can see that $T'$ has a trace class self-commutator. Observing that for any left-invertible operator $A \in \mathcal {B}(\mathcal {H})$ the following operator identities hold (cf. the proof of [12, Proposition 2.21]):

(6.6)\begin{equation} \begin{aligned}\ [A^*,A]A &\mathop =\limits^{(3.1)} -A^*A[A'^*,A']AA^*A, \\ [A^*, A] &\mathop =\limits^{(3.1)} ([A^*,A]A)A'^* + [A^*,A]P, \end{aligned} \end{equation}

where $P$ denotes the orthogonal projection of $\mathcal {H}$ onto $\ker A^*,$ and using the fact that the set of trace class operators is an ideal (see [39, Theorem 3.6.6]), we deduce that $T$ has a trace class self-commutator.

To prove the ‘moreover’ part we proceed as follows. First, we show that

(6.7)\begin{equation} \sigma(S) = \bar{\mathbb{D}}\ {\rm and}\ \sigma_{e}(S) = \sigma_{ap}(S) =\partial \mathbb{D}\ {\rm for}\ S \in \{T,T'\}. \end{equation}

Since $T$ is analytic, we see that $0\in \sigma (T)$. In view of the above discussion, $T$ and $T'$ are finitely cyclic. Let $S$ be any of the operators $T$ or $T'.$ It follows from Corollary 5.7 and Lemma 6.3 that $\sigma (S)=\overline {\mathbb {D}}$ and $\sigma _{e}(S) \subseteq \sigma _{ap}(S)=\partial {\mathbb {D}}$. However, if $\lambda \in \partial {\mathbb {D}}=\partial \sigma (S)$, then by [17, Theorem XI.6.8] either $\lambda$ is an isolated point of $\sigma (S)$ (which is not the case) or $\lambda \in \sigma _{e}(S)$, meaning that $\partial {\mathbb {D}} \subseteq \sigma _{e}(S)$. Putting all this together, we conclude that $\sigma _{e}(S) = \sigma _{ap}(S) =\partial \mathbb {D}$, which completes the proof of (6.7).

Next, applying (6.7) and the fact that $\mathrm {ind}_S(\cdot )$ is constant on connected components of $\mathbb {C} \backslash \sigma _{e}(S)$ (use [17, Corollary XI.3.13]), we deduce that

(6.8)\begin{align} \mathrm{ind}_{T}(\lambda) & =\mathrm{ind}_{T}(0)\nonumber\\ & \mathop =\limits^{(6.4)} - \dim\ker T^*\nonumber\\ & ={-} \dim \ker T^{\prime *} \nonumber\\ & \mathop =\limits^{(6.4)}\mathrm{ind}_{T'}(0) =\mathrm{ind}_{T'}(\lambda), \quad \lambda\in\mathbb{D}. \end{align}

It follows from [11, Theorem 8.1] that for any $\lambda \in \mathbb {C} \backslash \sigma _{e}(S)$, the Pincus principal function $\mathcal {P}_S(\cdot )$ of a completely non-normal operator $S$ with a trace class self-commutator is equal to $\mathrm {ind}_{S}(\lambda )$ a.e. with respect to the planar Lebesgue measure in a neighbourhood of $\lambda$. By Corollary 3.3(ii) and [6, Proposition 2.2], $T$ and $T'$ are completely non-normal, and thus by (6.7) and (6.8), we deduce that

(6.9)\begin{equation} \mathcal{P}_T(\lambda)= \mathcal{P}_{T'}(\lambda)={-} \dim \ker T^* \cdot \chi_{\mathbb{D}}(\lambda)\quad \text{for a.e.}\ \lambda\in \mathbb{C}, \end{equation}

where $\chi _{\mathbb {D}}$ stands for the characteristic function of $\mathbb {D}$. Since the Carey–Pincus trace formula for polynomials in $S$ and $S^*$ is valid for completely non-normal operators $S$ with a trace class self-commutator (see [11, Theorem 5.1]; see also [21, Theorem, p. 148]), the proof is complete.

The following is a corollary from the proof of Theorem 1.4.

Corollary 6.4 Suppose that $\mathcal {H}\neq \{0\}$ and $T \in \mathcal {B}(\mathcal {H})$ is an analytic finitely cyclic operator satisfying the conditions (1.1) and (1.2) of Definition 1.1. Then

(6.10)\begin{equation} \begin{aligned} & \sigma_{le}(T) =\sigma_{re}(T)=\sigma_{e}(T)=\sigma_{ap}(T) = \partial \mathbb{D}, \\ & \sigma_{le}(T')=\sigma_{re}(T')=\sigma_{e}(T')=\sigma_{ap}(T') = \partial \mathbb{D}. \end{aligned} \end{equation}

Moreover, $\dim \ker (T^*)$ is a positive integer and

(6.11)\begin{equation} \mathrm{ind}_{T}(\lambda) =\mathrm{ind}_{T'}(\lambda) = \begin{cases} - \dim \ker T^* & \text{if } \lambda \in\mathbb{D}, \\ 0 & \text{if } \lambda \in \mathbb{C}{\setminus} \overline{\mathbb{D}}. \end{cases} \end{equation}

Proof. A careful look at [17, Theorem XI.6.8] and the proofs of (6.7) and (6.8) yields (6.10) and (6.11). That $\dim \ker (T^*)$ is a positive integer can be inferred from (6.10), (6.11) and the fact that the Fredholm index $\mathrm {ind}_S(\cdot )$ of any $S\in \mathcal {B}(\mathcal {H})$ is constant on connected components of $\mathbb {C}\backslash \sigma _{e}(S).$

Remark 6.5 Let us mention that the identity $\sigma _{e}(S) =\partial \mathbb {D}$ which appears in (6.7) can be proved without using [17, Theorem XI.6.8]. Indeed, as in the proof of (6.7), we see that $\sigma _{e}(S) \subseteq \sigma _{ap}(S) = \partial {\mathbb {D}}$, where $S \in \{T,T'\}$. Suppose, to the contrary, that $\sigma _{e}(S)$ is a proper subset of $\partial {\mathbb {D}}$. Then

\[ \mathbb{D}\cup (\mathbb{C} {\setminus}\overline{\mathbb{D}}) \subseteq \mathbb{C} {\setminus} \sigma_{e}(S). \]

Since, in general, $\mathrm {ind}_S(\cdot )$ is constant on connected components of $\mathbb {C} {\setminus} \sigma _{e}(S)$, and in our case $\mathbb {C} {\setminus} \sigma _{e}(S)$ is connected, by Corollary 5.7(i), $\mathrm {ind}_{S}(\lambda )=0$ whenever $\lambda \in \mathbb {C} {\setminus} \overline {\mathbb {D}}$. We conclude that (recall that $\dim \ker T^* = \dim \ker T^{\prime *}$)

\[ - \dim \ker T^* \mathop =\limits^{(6.4)}\mathrm{ind}_{S}(0) = \mathrm{ind}_{S}(\lambda) = 0, \quad \lambda \in \mathbb{C} {\setminus}\overline{\mathbb{D}}. \]

This implies that $T$ is invertible, which contradicts $0\in \sigma (T)$. $\diamondsuit$

7. Generalizations to the classes $\mathcal {A}_{k}$

Motivated by the study of weakly concave operators, we introduce and discuss the following related classes of operators.

Definition 7.1 Let $T\in \mathcal {B}(\mathcal {H})$. We say that $T$ is of class $\mathcal {A}_{\infty }$ if

1. (i) $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$,

2. (ii) $T$ is an expansion,

3. (iii_∞) $T'|_{\mathcal {H}_u'}$ is hyponormal with $\mathcal {H}_u'=\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^{\prime n})$.

Given $k \in \mathbb {Z}_+,$ we say that $T$ is of class $\mathcal {A}_{k}$ if (i), (ii) and (iii$_{k}$) hold, where

1. (iii_k) $T'|_{{\mathcal {R}}(T'^k)}$ is hyponormal.

It follows from [36, p. 294] and Proposition 3.1 that the class $\mathcal {A}_0$ contains all concave operators and the class $\mathcal {A}_1$ consists exactly of weakly concave operators. Since the restriction of a hyponormal operator to its closed invariant subspace is again hyponormal, we conclude that

(7.1)\begin{equation} \{concave\ operators\} \subseteq \mathcal{A}_{k} \subseteq \mathcal{A}_{k+1} \subseteq \mathcal{A}_{\infty}, \quad k\in \mathbb{Z}_+. \end{equation}

It turns out that all inclusions in (7.1) are proper if $\mathcal {H}$ is infinite dimensional (see Example 7.6). If $\mathcal {H}$ is finite dimensional, then for every $k\in \mathbb {Z}_+ \cup \{\infty \}$, $\mathcal {A}_k$ consists exactly of unitary operators [see Proposition 3.2(i)].

An examination of the proof of Theorem 1.3 (using Proposition 3.2(i) in place of Corollary 3.3(i)) shows that it is true for operators of class $\mathcal {A}_{k}$, where $k\in \mathbb {Z}_+ \cup \{\infty \}$.

Theorem 7.2 Suppose that $T \in \mathcal {B}(\mathcal {H})$ is of class $\mathcal {A}_{\infty }$. Let $\mathcal {H}_u$ and $\mathcal {H}'_u$ denote the closed vector subspaces of $\mathcal {H}$ given by (1.4). Then $\mathcal {H}'_u \subseteq \mathcal {H}_u$ and $\mathcal {H}'_u$ reduces $T.$ Moreover,

\[ T = U \oplus S\ \text{with respect to the decomposition}\ \mathcal{H} = \mathcal{H}'_u \oplus (\mathcal{H}'_u)^{{\perp}}, \]

where $U \in \mathcal {B}(\mathcal {H}'_u)$ is unitary and $S \in \mathcal {B}((\mathcal {H}'_u)^{\perp })$ has the wandering subspace property.

Remark 7.3 Regarding Theorems 1.3 and 7.2, we make the following observation. Let $T \in {\mathcal {B}}(\mathcal {H})$ be an analytic expansion with $\sigma _{ap}(T) \subseteq \partial \mathbb {D}$ and let $T'$ be the Cauchy dual of $T.$ Set $R:=T'|_{\mathcal {H}'_u}$. Since the analyticity of $T$ implies that $0\in \sigma (T)$, it can be concluded from the proof of Theorem 1.3 that $R$ is an invertible contraction such that $\sigma _{ap}(R) \subseteq \partial \mathbb {D}$ (see (6.1)), which together with the inclusion $\partial \sigma (R) \subseteq \sigma _{ap}(R)$ implies that $\sigma (R) \subseteq \partial \mathbb {D}$ (the reader is referred to [41, Theorem 7], where a non-unitary contraction with spectrum being a nowhere dense perfect set of measure zero on the unit circle has been constructed). Thus $R$ is unitary if and only if $R$ is hyponormal. In particular, this is the case if the restriction of $T'$ to the range of some power of it is hyponormal [see (7.1) and Theorem 7.2]. $\diamondsuit$

In turn, Theorem 1.4 remains valid for operators of class $\mathcal {A}_{k}$, where $k\in \mathbb {Z}_+$.

Theorem 7.4 Let $T \in \mathcal {B}(\mathcal {H})$ be an analytic finitely cyclic operator of class $\mathcal {A}_{k}$ for some $k\in \mathbb {Z}_+.$ Then $T$ and $T'$ have trace class self-commutators. Moreover, for any complex polynomials $p, q$ in two complex variables $z$ and $\bar z$,

\begin{align*} \mathrm{tr}\,[p(T', T'^*), q(T', T'^*)] & =\mathrm{tr}\,[p(T, T^*), q(T, T^*)] \\ & = \frac{1}{\pi}\dim \ker T^* \int_{\mathbb{D}} \left(\frac{\partial p}{\partial \bar z}\frac{\partial q}{\partial z} - \frac{\partial p}{\partial z}\frac{\partial q}{\partial \bar z}\right) (z, \bar z)\,dA(z), \end{align*}

where $dA$ denotes the Lebesgue planar measure.

Proof. According to Proposition 3.1, the case $k=1$ is precisely Theorem 1.4 (by (7.1), this implies the case $k=0$). Assume now that $k \geqslant 2.$ Since $T$ is finitely cyclic, we infer from (6.2) that $\dim \ker T^* < \infty$. By the analyticity of $T$, $\mathcal {H}_u=\{0\}$, so by [35, Proposition 2.7(ii)] $T'$ is finitely cyclic with the cyclic space $\ker T^*$. Since the range of $T^{\prime k}$ is closed, we deduce that $R_k:=T'|_{{\mathcal {R}}(T^{\prime k})}$ is finitely cyclic with the cyclic space $T^{\prime k}(\ker T^*)$ (cf. (6.5)). By (${\rm iii}_{k}$), $R_k$ is hyponormal, so by [18, Theorem IV.2.1], $[R_k^*,R_k]$ is of trace class. It follows from [35, Lemma 2.1] that

\[ {\mathcal{R}}(T^{\prime k})^{{\perp}}=\ker{T^{\prime * k}}=\bigvee_{j=0}^{k-1} T^j(\ker T^*), \]

which yields $\dim {\mathcal {R}}(T^{\prime k})^{\perp } <\infty$. This implies that $T'$ is a finite rank perturbation of the operator $R_k \oplus 0$ which has a trace class self-commutator. Thus, the self-commutator of $T'$ and consequently that of $T$ are of trace class (see (6.6)). It is also easy to see that (6.7) holds (with the same proof). Next, arguing as in last paragraph of the proof of Theorem 1.4 [with Proposition 3.2(ii) in place of Corollary 3.3(ii)], we conclude that (6.9) holds. Finally, applying the Carey–Pincus trace formula completes the proof.

The next result generalizes [12, Corollary 2.29], which was stated for concave operators, to operators of class $\mathcal {A}_k$ with $k\in \mathbb {Z}_+$ (see (7.1)). This is also related to [16].

Corollary 7.5 Suppose that $\mathcal {H}\neq \{0\}$ and $T \in \mathcal {B}(\mathcal {H})$ is an analytic finitely cyclic operator of class $\mathcal {A}_{k},$ where $k\in \mathbb {Z}_+.$ Then $n: =\dim \ker T^*$ is a positive integer and $T$ is unitarily equivalent to a compact perturbation of $U^n_+$, where $U_+$ is the unilateral shift of multiplicity $1.$

Proof. By Corollary 6.4, $n$ is a positive integer. Next, note that $U_+^n$ is a concave operator which is analytic and finitely cyclic with $\dim \ker (U_+^{n})^{*}=n$. Applying Corollary 6.4 to the operators $T$ and $U_+^n$, we conclude that

(7.2)\begin{align} \sigma_{e}(T)& =\sigma_{e}(U_+^n)=\partial \mathbb{D}, \end{align}

(7.3)\begin{align} \mathrm{ind}_{T}(\lambda) & =\mathrm{ind}_{U_+^n}(\lambda), \quad \lambda\in \mathbb{C} {\setminus}\partial \mathbb{D}. \end{align}

By Theorem 7.4, the operators $T$ and $U_+^n$ have compact self-commutators. This together with (7.2), (7.3) and [19, Theorem 2] completes the proof.

The example below shows that if $\mathcal {H}$ is infinite dimensional, then all the inclusions in (7.1) are proper, i.e.,

(7.4)\begin{equation} \{concave\ operators\} \varsubsetneq \mathcal{A}_{k} \varsubsetneq \mathcal{A}_{k+1}\varsubsetneq \mathcal{A}_{\infty}, \quad k\in\mathbb{Z}_+, \end{equation}

and Theorem 7.4 is not true for operators of class $\mathcal {A}_{\infty }$.

Example 7.6 [Example 5.4 continued]

As in Example 5.4, we assume that the unilateral weighted shift $W$ is left-invertible. Clearly, $W$ is cyclic with the cyclic vector $e_0$ and is expansive if and only if

(7.5)\begin{equation} w_n \geqslant 1\ {\rm for\ all}\ n\in \mathbb{Z}_+. \end{equation}

Fix $k\in \mathbb {Z}_+$. Since $W$ and $W'$ are unilateral weighted shifts, we have

(7.6)\begin{equation} {\mathcal{R}}(W^k) = {\mathcal{R}}(W^{\prime k}) =\bigvee_{n=k}^{\infty} \mathbb{C} e_n. \end{equation}

This implies that $W$ and $W'$ are analytic. By (7.6), the operator $W'|_{{\mathcal {R}}(W^{\prime k})}$ is unitarily equivalent to the unilateral weighted shift with weights $\{w_{k+n}^{-1}\}_{n=0}^{\infty }$. Hence, by [18, Proposition II.6.6], $W'|_{{\mathcal {R}}(W^{\prime k})}$ is hyponormal if and only if

(7.7)\begin{equation} \text{the sequence}\ \{w_{k+n}\}_{n=0}^{\infty}\ \text{is monotonically decreasing.} \end{equation}

Consider now the inequality

(7.8)\begin{equation} \limsup_{n\to \infty} w_n\leqslant 1, \end{equation}

and note that the following implication is valid.

(7.9)\begin{equation} \textit{If}\ (7.8)\ holds, then\ r(W)\leqslant 1. \end{equation}

Indeed, if $\varepsilon > 0$, then $\sup _{n\geqslant l} w_n \leqslant 1+\varepsilon$ for some integer $l\geqslant 1$, so

\[ \sup_{n\geqslant 0} w_n \cdots w_{n+m-1} \leqslant M (1+\varepsilon)^m, \quad m \geqslant l+1, \]

with $M:= \max \left \{1, w_{l-1}, w_{l-1}\cdot w_{l-2}, \ldots, w_{l-1} \cdots w_{0}\right \}.$ By Gelfand's formula,

\[ r(W) = \lim_{m \to \infty} \|W^m\|^{1/m} =\lim_{m\to \infty} (\sup_{n\geqslant 0} w_n \cdots w_{n+m-1})^{1/m} \leqslant 1+ \varepsilon. \]

which yields $r(W)\leqslant 1$.

Combining (7.9) and Remark 1.2 with the analyticity of $W'$, we obtain the following sufficient condition for membership in the class² $\mathcal {A}_{\infty }$.

(7.10)\begin{equation} \textit{If}\ (7.5)\ and\ (7.8)\ hold, then\ W\ is\ of\ class\ \mathcal{A}_{\infty}. \end{equation}

Moreover, the following necessary and sufficient condition for membership in the class $\mathcal {A}_k$ with $k \in \mathbb {Z}_+$ can be deduced from [37, Proposition 15] and Remark 1.2.

(7.11)\begin{equation} W\ is\ of\ class\ \mathcal{A}_k\ if\ and\ only\ if\ (7.5), (7.7)\ and\ (7.8)\ hold. \end{equation}

It is now easy to deduce from (7.10) and (7.11) that

\[ \mathcal{A}_{k} \varsubsetneq \mathcal{A}_{k+1}\varsubsetneq \mathcal{A}_{\infty}, \quad k\in\mathbb{Z}_+. \]

To obtain the operator of class $\mathcal {A}_0$ that is not concave, we proceed as follows. By [25, Proposition A.2], the unilateral weighted shift $W$ with weight sequence $\left \{\frac {n+2}{n+1}\right \}_{n=0}^{\infty }$ is a strict $3$-isometric expansion. Since $W'$ is the unilateral weighted shift with weight sequence $\left \{\frac {n+1}{n+2}\right \}_{n=0}^{\infty }$ which is increasing, $W'$ is hyponormal, meaning that $W$ is of class $\mathcal {A}_0$. However, by Proposition 4.4, $W$ is not concave. This justifies all the strict inclusions in (7.4).

The modulus of the self-commutator $[W^*,W]$ of $W$ is the diagonal operator (relative to $\{e_n\}_{n=0}^{\infty }$) with diagonal elements $\{|w_n^2 - w_{n-1}^2|\}_{n=0}^{\infty }$, where $w_{-1}:=0$. Suppose that $k\in \mathbb {Z}_+$ and $W$ is of class $\mathcal {A}_k$. Then, by (7.11), we have

\begin{align*} \sum_{n=k+1}^{\infty} |w_n^2 - w_{n-1}^2| & \mathop =\limits^{(7.7)} \sum_{n=k+1}^{\infty} (w_{n-1}^2 - w_n^2) \\ & =\lim_{m\to \infty}\sum_{n=k+1}^{m} (w_{n-1}^2 - w_n^2) \\ & = \lim_{m\to \infty} (w_{k}^2 - w_m^2) \\ & \mathop =\limits^{(7.5) \& (7.8)} w_{k}^2 -1 < \infty, \end{align*}

which means that $[W^*,W]$ is of trace class. The above reasoning can be used to compute the trace $\mathrm {tr}\, [W^*,W]$ of the self-commutator $[W^*,W]$:

(7.12)\begin{equation} \mathrm{tr}\, [W^*,W] = \sum_{n=0}^{\infty} (w_n^2 - w_{n-1}^2) = \lim_{m\to \infty} w_m^2\mathop =\limits^{(7.5) \& (7.8)} 1. \end{equation}

Certainly, the fact that $W$ has a trace class self-commutator as well as the formula (7.12) are particular cases of what is in Theorem 7.4 with the polynomials $p(z,\bar z) = \bar z$ and $q(z,\bar z) = z$.

Consider now the case where $W$ satisfies (7.5) and (7.8). By (7.10), $W$ is of class $\mathcal {A}_{\infty }$. Clearly, $\lim _{n\to \infty } w_n=1$. Then $[W^*,W]$, being the diagonal operator with diagonal elements $\{w_n^2 - w_{n-1}^2\}_{n=0}^{\infty }$ converging to $0$, is compact.

Now we construct a unilateral weighted shift $W$ of class $\mathcal {A}_{\infty }$ such that the self-commutator $[W^*,W]$ of $W$ is not of trace class (recall that $W$ is analytic and cyclic). Let $\{w_n\}_{n=0}^{\infty }$ be defined by

\[ \mathop{\underbrace{\alpha_1,\alpha_2, \alpha_1, \alpha_2, \alpha_1}}\limits_{5\ \text{times}},\ldots, \mathop{\underbrace{\alpha_l, \alpha_{l+1}, \ldots, \alpha_l, \alpha_{l+1}, \alpha_l}}\limits_{2^{l+1} + 1\text{ times}},\ldots, \]

where $\alpha _l = \sqrt {1+\frac 1{2^l}}$ for $l=1,2,\ldots$. Straightforward computations show that

\[ \sum_{n=0}^{\infty} |w_n^2 - w_{n-1}^2| = \infty, \]

which means that $[W^*,W]$ is not of trace class. Since $W$ satisfies (7.5) and (7.8), we infer from (7.10) that $W$ is of class $\mathcal {A}_{\infty }$. $\diamondsuit$

As shown in Example 7.6 (see its last paragraph), Theorem 7.4 ceases to be true for operators of class $\mathcal {A}_{\infty }$. However, in this example $\mathcal {H}_{u}'=\{0\}$ and the operator in question has a compact self-commutator. This motivates us to ask the following question which is closely related to Corollaries 6.4 and 7.5.

Question 7.7 Is an analytic finitely cyclic operator $T$ of class $\mathcal {A}_{\infty }$ unitarily equivalent to a compact perturbation of $U^n_+$, where $n=\dim \ker (T^*)$?

8. Characterizations of classes $\mathcal {A}_k$

In this section, we characterize the left-invertible operators $T$ satisfying the condition (${\rm iii}_{k}$) of Definition 7.1, where $k\in \mathbb {Z}_+ \cup \{\infty \}$. In particular, we obtain characterizations of classes $\mathcal {A}_k.$ We begin with an observation of independent interest.

Lemma 8.1 Let $T \in \mathcal {B}(\mathcal {H})$ be left-invertible and let $k$ be a positive integer. Then the range of $T'^k$ is given by

\[ {\mathcal{R}}(T^{\prime k}) = \bigcap_{j=0}^{k-1} \ker((I - T'T^*)T^{*j}). \]

Proof. Using [35, Lemma 2.1], the fact that the range of $T^{\prime k}$ is closed and finally Proposition 2.1(iii), we get

\begin{align*} {\mathcal{R}}(T^{\prime k}) & = \left(\bigvee_{j=0}^{k-1} T^j(\ker T^*)\right)^{{\perp}} \\ & = \bigcap_{j=0}^{k-1} \left(T^j(\ker T^*)\right)^{{\perp}} \\ & = \bigcap_{j=0}^{k-1}\left({\mathcal{R}}(T^j(I-P_{{\mathcal{R}}(T)}))\right)^{{\perp}} \\ & = \bigcap_{j=0}^{k-1} \ker((I - T'T^*)T^{*j}). \end{align*}

This completes the proof.

The hyponormality of $T'|_{{\mathcal {R}}(T^{\prime k})}$ can now be characterized as follows.

Proposition 8.2 Let $T \in \mathcal {B}(\mathcal {H})$ be left-invertible and $k\in \mathbb {Z}_+$. Set $C_k = T^{\prime *k} T^{\prime k}$. Then $C_k$ is invertible and the following conditions are equivalent:

1. (i) $T'|_{{\mathcal {R}}(T^{\prime k})}$ is hyponormal,

2. (ii) $C_k^{1/2} T' C_k^{-1/2}$ is hyponormal.

Proof. Since $T^{\prime k}$ is left-invertible, $C_k$ is invertible and, by Proposition 2.1(iii), we have

(8.1)\begin{equation} P_{{\mathcal{R}}(T^{\prime k})} = T^{\prime k}(T^{\prime *k}T^{\prime k})^{{-}1}T^{\prime *k} = T^{\prime k}C_k^{{-}1}T^{\prime *k}. \end{equation}

It is easily seen that $T'|_{{\mathcal {R}}(T^{\prime k})}$ is hyponormal if and only if

\[ T^{\prime *k} T^{\prime} P_{{\mathcal{R}}(T^{\prime k})}T^{\prime *} T^{\prime k} \leqslant T^{\prime *(k+1)} T^{\prime (k+1)}, \]

or equivalently, by (8.1), if and only if

\[ C_k T' C_k^{{-}1} T^{\prime *} C_k \leqslant T^{\prime *} C_k T^{\prime}, \]

which in turn is equivalent to

\[ C_k^{1/2} T' C_k^{{-}1} T^{\prime *} C_k^{1/2} \leqslant C_k^{{-}1/2} T^{\prime *} C_k T^{\prime} C_k^{{-}1/2}. \]

As a consequence, $T'|_{{\mathcal {R}}(T^{\prime k})}$ is hyponormal if and only if

\[ \|(C_k^{1/2} T^{\prime} C_k^{{-}1/2})^* h\|^2 \leqslant \|(C_k^{1/2} T^{\prime} C_k^{{-}1/2}) h\|^2, \quad h \in \mathcal{H}, \]

which completes the proof.

Corollary 8.3 Suppose that $T\in \mathcal {B}(\mathcal {H})$ is left-invertible and $T=U|T|$ is the polar decomposition of $T.$ Then $T'|_{{\mathcal {R}}(T')}$ is hyponormal if and only if $|T|^{-1} U$ is hyponormal. In particular, if $T'$ is hyponormal, then $|T|^{-1} U$ is hyponormal.

Proof. It follows from Proposition 2.1(i) that

\[ C_1^{1/2} T' C_1^{{-}1/2} = |T|^{{-}1} T |T|^{{-}1} = |T|^{{-}1} U. \]

Combined with Proposition 8.2, this completes the proof.

Corollary 8.4 If $T\in \mathcal {B}(\mathcal {H})$ is of class $\mathcal {A}_k$ for some $k\in \mathbb {Z}_+$, then $T'$ is similar to a hyponormal operator.

Corollary 8.5 Let $T \in \mathcal {B}(\mathcal {H})$ be an operator of class $\mathcal {A}_k$ for some $k\in \mathbb {Z}_+.$ Then the operator $S_k:=C^{1/2}_k T' C^{-1/2}_k$ is a $2$-hypercontraction, that is

(8.2)\begin{equation} \sum_{j=0}^m ({-}1)^j \binom{m}{j} S_k^{*j}S_k^j \geqslant 0, \quad m=1,2. \end{equation}

In particular,

(8.3)\begin{equation} T^{\prime *k}(I - 2 T^{\prime *}T' + T^{\prime * 2}T'^2)T^{\prime k} \geqslant 0. \end{equation}

Proof. By Proposition 7.2, the operator $S_k$ is hyponormal. It follows that

\[ I - 2S_k^*S_k + S_k^{*2}S_k^2 \geqslant I - 2S_k^*S_k + S_k^{*}S_kS_k^*S_k = (I-S_k^*S_k)^2 \geqslant 0, \]

which gives (8.2) for $m=2$ (this is true for all hyponormal operators). It is now easy to see that (8.2) for $m=2$ is equivalent to

\[ C_k - 2T^{\prime *}C_kT^{\prime} + T^{\prime *2}C_kT^{\prime 2} \geqslant 0, \]

which in turn is equivalent to (8.3).

Since $T^*T \geqslant I,$ we deduce that

\[ C_1=T^{\prime *} T^{\prime} = (T^*T)^{{-}1} \leqslant I. \]

Consequently, we have

\[ C_{k+1} = T^{\prime * k} C_1 T^{\prime k} \leqslant T^{\prime * k} T^{\prime k} = C_k, \quad k \in\mathbb{Z}_+, \]

or equivalently that

\[ C_k^{{-}1/2}C_{k+1} C_k^{{-}1/2} \leqslant I, \quad k\in\mathbb{Z}_+. \]

This gives

\[ S_k^*S_k = C^{{-}1/2}_k T^{\prime *} C_k T' C^{{-}1/2}_k = C^{{-}1/2}_k C_{k+1} C^{{-}1/2}_k \leqslant I, \quad k\in \mathbb{Z}_+, \]

which shows that (8.2) holds for $m=1.$ This completes the proof.

Remark 8.6 Regarding the operator $C_k^{1/2} T' C_k^{-1/2}$ that appears in Proposition 8.2, observe that if $A\in \mathcal {B}(\mathcal {H})$ is positive and invertible and $T\in \mathcal {B}(\mathcal {H})$, then the adjoint of $T$ with respect to the (equivalent) inner product $\langle {A(\cdot )},\,{-} \rangle$, is equal to $(ATA^{-1})^*$. In turn, if $T\in \mathcal {B}(\mathcal {H})$ is left-invertible and $T=U|T|$ is the polar decomposition of $T$, then by Proposition 2.1, $T'= U|T|^{-1}$ is the polar decomposition of $T',$ so the operator $|T|^{-1} U$ that appears in Corollary 8.3 is the Duggal transform³ of $T'.$ Finally, the concept of $m$-hypercontractivity that appears in Corollary 8.5 was introduced by Agler in [2]. $\diamondsuit$

The following characterization of the hyponormality of $T'|_{\mathcal {H}_{u}'}$ can be viewed as an asymptotic version of Proposition 8.2 (see Remark 8.8).

Proposition 8.7 Let $T \in \mathcal {B}(\mathcal {H})$ be left-invertible and let $C_k = T^{\prime *k} T^{\prime k}$ for $k\in \mathbb {Z}_+$. Then $\{T^{\prime (k+1)} C_k^{-1} T^{\prime * (k+1)}\}_{k=0}^{\infty }$ and $\{T^{\prime k}C_k^{-1} C_{k+1} C_k^{-1} T^{\prime * k}\}_{k=0}^{\infty }$ converge in SOT $($the strong operator topology$)$ to positive operators denoted by $A$ and $B$, respectively, and the following conditions are equivalent:

1. (i) $T'|_{\mathcal {H}_{u}'}$ is hyponormal,

2. (ii) $A \leqslant B$,

3. (iii) for all $h\in \mathcal {H}$,

   \[ \lim_{k\to \infty} \|(C_k^{1/2}T'C_k^{{-}1/2})^* C_k^{{-}1/2} T^{\prime * k}h\|^2 \leqslant \lim_{k\to\infty} \|C_k^{1/2}T'C_k^{{-}1/2} C_k^{{-}1/2} T^{\prime * k}h\|^2, \]

4. (iv) $P_{\mathcal {H}_{u}'} ((T^*T)^{-1} - T^{\prime } P_{\mathcal {H}_{u}'} T^{\prime *}) P_{\mathcal {H}_{u}'} \geqslant 0$.

Moreover, $A=P_{\mathcal {H}_{u}'} T^{\prime } P_{\mathcal {H}_{u}'} T^{\prime *} P_{\mathcal {H}_{u}'}$ and $B=P_{\mathcal {H}_{u}'} (T^*T)^{-1} P_{\mathcal {H}_{u}'}.$

Proof. Set $P_k=P_{{\mathcal {R}}(T^{\prime k})}$ for $k \in \mathbb {Z}_+$ and $P_{\infty } = P_{\mathcal {H}_{u}'}$. Since ${\mathcal {R}}(T^{\prime k}) \searrow \mathcal {H}_{u}'$ as $k\nearrow \infty$, we deduce that $P_k \searrow P_{\infty }$ as $k\nearrow \infty$ in SOT. By the sequential SOT-continuity of multiplication in $\mathcal {B}(\mathcal {H})$, we deduce that

(8.4)\begin{align} \left. \begin{array}{c}the\ sequences\ \{P_k T^{\prime *} P_k\}_{k=0}^{\infty}\ and\ \{(P_k T^{\prime *} P_k)^*P_k T^{\prime *} P_k\}_{k=0}^{\infty}\\ converge\ in\ SOT\ to\ P_{\infty} T^{\prime *} P_{\infty}\ and\ P_{\infty} T^{\prime} P_{\infty} T^{\prime *} P_{\infty}, respectively,\end{array}\right\} \end{align}

(8.5)\begin{align} \left. \begin{array}{c}the\ sequences\ \{T' P_k\}_{k=0}^{\infty}\ and\ \{(T'P_k)^*T'P_k\}_{k=0}^{\infty}\ converge\\ in\ SOT\ to\ T'P_{\infty}\ and\ P_{\infty} T^{\prime *} T^{\prime} P_{\infty} = P_{\infty} (T^*T)^{{-}1} P_{\infty}, respectively.\end{array}\right\} \end{align}

Observe now that,

\[ P_k T^{\prime *} P_k \mathop =\limits^{(8.1)} T^{\prime k}C_k^{{-}1}T^{\prime *k} T^{\prime *} T^{\prime k}C_k^{{-}1}T^{\prime *k} = T^{\prime k}C_k^{{-}1}T^{\prime *(k+1)}, \quad k\in \mathbb{Z}_+, \]

which yields

(8.6)\begin{align} (P_k T^{\prime *} P_k)^*P_k T^{\prime *} P_k & = T^{\prime (k+1)}C_k^{{-}1} T^{\prime * k} T^{\prime k}C_k^{{-}1}T^{\prime *(k+1)}\nonumber\\ & =T^{\prime (k+1)}C_k^{{-}1} T^{\prime *(k+1)}, \quad k\in\mathbb{Z}_+. \end{align}

Combined with (8.4), this implies that the sequence $\{T^{\prime (k+1)}C_k^{-1} T^{\prime *(k+1)}\}_{n=0}^{\infty }$ converges in SOT to $A=P_{\infty } T^{\prime } P_{\infty } T^{\prime *} P_{\infty }$, and

(8.7)\begin{equation} \langle{Ah},h \rangle= \lim_{k\to \infty} \|(C_k^{1/2}T'C_k^{{-}1/2})^* C_k^{{-}1/2} T^{\prime * k}h\|^2, \quad h\in \mathcal{H}. \end{equation}

A similar argument shows that

(8.8)\begin{equation} (T'P_k)^*T'P_k = T^{\prime k}C_k^{{-}1} C_{k+1}C_k^{{-}1}T^{\prime *k}, \quad k\in \mathbb{Z}_+, \end{equation}

so by (8.5) the sequence $\{T^{\prime k}C_k^{-1} C_{k+1} C_k^{-1} T^{\prime * k}\}_{n=0}^{\infty }$ converges in SOT to $B=P_{\infty } (T^*T)^{-1} P_{\infty }$, and moreover:

(8.9)\begin{equation} \langle{Bh},h \rangle= \lim_{k\to \infty} \|(C_k^{1/2}T'C_k^{{-}1/2}) C_k^{{-}1/2} T^{\prime * k}h\|^2,\quad h\in \mathcal{H}. \end{equation}

(i)$\Leftrightarrow$(ii) It is easy to see that $T'|_{\mathcal {H}_{u}'}$ is hyponormal if and only if

\[ \|P_{\infty} T^{\prime *} P_{\infty} h\|^2 \leqslant \|T' P_{\infty} h\|^2, \quad h \in \mathcal{H}, \]

or equivalently, by (8.4) and (8.5), if and only if

\[ \lim_{k\to \infty} \|P_k T^{\prime *} P_k h\|^2 \leqslant \lim_{k\to \infty} \|T'P_k h\|^2, \quad h\in \mathcal{H}. \]

Combined with (8.6) and (8.8), this shows that (i) and (ii) are equivalent.

(ii)$\Leftrightarrow$(iii) This follows from (8.7) and (8.9).

(ii)$\Leftrightarrow$(iv) This is a consequence of the identities $A=P_{\infty } T^{\prime } P_{\infty } T^{\prime *} P_{\infty }$ and $B=P_{\infty } (T^*T)^{-1} P_{\infty }$.

Remark 8.8 Regarding Proposition 8.7(iii), note that in view of Proposition 2.1(i) applied to $T^{\prime k}$, the operator $T^{\prime k}C_k^{-1/2}$ is an isometry. This implies that the range of $C_k^{-1/2} T^{\prime * k}$ is equal to $\mathcal {H}$. As a consequence, for a fixed $k\in \mathbb {Z}_+$, the inequality

\[ \|(C_k^{1/2}T'C_k^{{-}1/2})^* C_k^{{-}1/2} T^{\prime * k}h\|^2 \leqslant \|C_k^{1/2}T'C_k^{{-}1/2} C_k^{{-}1/2} T^{\prime * k}h\|^2, \quad h\in \mathcal{H}, \]

is equivalent to

\[ \|(C_k^{1/2}T'C_k^{{-}1/2})^* h\|^2 \leqslant \|C_k^{1/2}T'C_k^{{-}1/2} h\|^2, \quad h\in \mathcal{H}, \]

which according to Proposition 8.2 is equivalent to the hyponormality of $T'|_{{\mathcal {R}}(T^{\prime k})}$. From this point of view, Proposition 8.7 can be seen as an asymptotic version of Proposition 8.2. $\diamondsuit$

9. $C^*$- and $W^*$-algebra analogues of $\mathcal {A}_k$

We conclude the paper by discussing the possibility of defining membership in the classes $\mathcal {A}_k$, $k\in \mathbb {Z}_+ \cup \{\infty \}$, for elements of an abstract unital $C^*$-algebra. This question is in the spirit of [9, 10, 42].

Let $\mathcal {C}$ be a $C^*$-algebra with unit $e.$ Set $\mathcal {C}_r := \{t\in \mathcal {C}\colon \|t\|\leqslant r\}$ for $r\in (0,\infty ).$ Fix $t\in \mathcal {C}$. Denote by $C^*(t)$ the $C^*$-algebra generated by $t$ and $e.$ We say that $t$ is hyponormal if $t^*t - tt^*$ is a positive element of $\mathcal {C}$. If $t^*t$ is invertible, then the element $t':= t (t^*t)^{-1}$ is called the Cauchy dual of $t$. Clearly, if $t^*t$ is invertible, then $t$ is left-invertible (with the left-inverse $t^{\prime *}$). The converse implication is true, as can be seen by using the Gelfand–Naimark representation theorem (see [33, Theorem 12.41]) and [17, Proposition VIII.1.14]. Namely, the following equivalences are valid:

(9.1)\begin{equation} t^*t\ is\ invertible\ \Leftrightarrow t^*t \geqslant \varepsilon e\ for\ some\ \varepsilon > 0 \Leftrightarrow t\ is\ \textit{left-invertible.} \end{equation}

In particular, if $t$ is an expansion, that is $t^*t \geqslant e$, then $t$ is left-invertible. Moreover, if $t$ is left-invertible, then so is $t'$ and consequently $t^{\prime k}$ for every $k\in \mathbb {Z}_+$. As a consequence of (9.1), $c_k := t^{\prime *k} t^{\prime k}$ is invertible. Observe also that if $t\in \mathcal {C}$ is left-invertible, then $t=(t^{\prime })^{\prime }$ so by (9.1) and [17, Proposition VIII.1.14], the $C^*$-algebras $C^*(t)$ and $C^*(t^{\prime })$ coincide. We now give the $C^*$-algebra analogue of the class $\mathcal {A}_k$ for $k\in \mathbb {Z}_+.$

Definition 9.1 Let $\mathcal {C}$ be a unital $C^*$-algebra and let $k\in \mathbb {Z}_+.$ We say that $t\in \mathcal {C}$ is of class $\mathcal {A}_k$ if

• • the spectral radius of $t$ is at most $1$,

• • $t$ is an expansion,

• • $c_k^{1/2} t' c_k^{-1/2}$ is hyponormal.

Using Remark 1.2 and Proposition 8.2, we see that Definitions 7.1 and 9.1 coincide for $k\in \mathbb {Z}_+$ if $\mathcal {C} = \mathcal {B}(\mathcal {H})$.

Remark 9.2 First observe that if $\mathcal {C}$ is a $C^*$-algebra with unit $e$ and $t\in \mathcal {C}$ is of class $\mathcal {A}_k$ for some $k\in \mathbb {Z}_+,$ then $C^*(t)$ is commutative if and only if $t$ is unitary, that is, $t^*t=tt^*=e.$

Note that if $t$ is a left-invertible element of a unital $C^*$-algebra $\mathcal {C}$, then $t^{\prime }=t$ if and only if $t$ is an isometric element of $\mathcal {C}$ (use the fact that $t^{\prime *}$ is a left-inverse of $t$). It is worth mentioning that the $C^*$-algebra generated by a single isometry was studied in [16].

If $\mathcal {C}_1$ and $\mathcal {C}_2$ are two unital $C^*$-algebras, $\pi \colon \mathcal {C}_1 \to \mathcal {C}_2$ is a $*$-isomorphism and $t_1\in \mathcal {C}_1$ and $t_2\in \mathcal {C}_2$ are such that $\pi (t_1) = t_2,$ then for each $k\in \mathbb {Z}_+$, $t_1$ is of class $\mathcal {A}_k$ if and only if $t_2$ is of class $\mathcal {A}_k.$ $\diamondsuit$

The case of the class $\mathcal {A}_{\infty }$ is more delicate. As we will show below, the membership in this class can be satisfactorily defined in the context of $W^*$-algebras, which are more special objects compared to $C^*$-algebras (see Definitions 9.6 and 9.7). Several properties of certain sequences associated with an expansion are needed for this.

Proposition 9.3 Let $\mathcal {C}$ be a $C^*$-algebra with unit $e$ and $t\in \mathcal {C}$ be an expansion. Define the sequences $\{p_k\}_{k=0}^{\infty },$ $\{u_k\}_{k=0}^{\infty }$ and $\{v_k\}_{k=0}^{\infty }$ in $\mathcal {C}$ by

(9.2)\begin{equation} p_k=t^{\prime k}c_k^{{-}1}t^{\prime *k}, u_k= t^{\prime (k+1)} c_k^{{-}1} t^{\prime * (k+1)}\ and\ v_k = t^{\prime k}c_k^{{-}1} c_{k+1} c_k^{{-}1} t^{\prime * k}. \end{equation}

Then the following statements hold for all $k\in \mathbb {Z}_+$:

1. (i) $p_k=p_k^*p_k,$ $p_kp_{k+1}=p_{k+1}$ and $0 \leqslant p_{k+1} \leqslant p_k \leqslant e,$

2. (ii) $0 \leqslant c_{k+1} \leqslant c_k \leqslant e$ and $c_k^{-1/2} c_{k+1} c_k^{-1/2} \leqslant e,$

3. (iii) $u_k=t^{\prime } p_k t^{\prime *},$ $0 \leqslant t^{\prime (k+1)} t^{\prime * (k+1)} \leqslant u_k \leqslant p_{k+1} \leqslant e$ and $u_{k+1} \leqslant u_k,$

4. (iv) $v_{k+1} = p_{k+1} v_k p_{k+1},$ $v_k = p_k t^{\prime *}t^{\prime } p_k$ and $0 \leqslant v_k \leqslant p_k \leqslant e.$

Moreover, $t$ is an expansive element of $C^*(t)$ and the elements $t^{\prime }$, $c_k$, $c_k^{-1}$, $p_k$, $u_k$ and $v_k$ belong to $C^*(t).$

Proof. (i) By definition, $p_k=p_k^*$ and

(9.3)\begin{equation} p_k^2 = t^{\prime k}c_k^{{-}1}(t^{\prime *k} t^{\prime k})c_k^{{-}1}t^{\prime *k} =p_k, \quad k\in \mathbb{Z}_+, \end{equation}

so $p_k=p_k^*p_k$ for all $k\in \mathbb {Z}_+.$ Since

(9.4)\begin{equation} p_kp_{k+1} = t^{\prime k}c_k^{{-}1}(t^{\prime *k} t^{\prime k})t' c_{k+1}^{{-}1}t^{\prime *(k+1)}= p_{k+1}, \quad k\in \mathbb{Z}_+, \end{equation}

and thus $p_kp_{k+1}=p_{k+1}p_k$ for all $k\in \mathbb {Z}_+,$ we deduce that

\[ (p_k-p_{k+1})^2 \mathop =\limits^{(9.3)} p_k - 2 p_k p_{k+1} + p_{k+1} \mathop =\limits^{(9.4)} p_k-p_{k+1}, \quad k \in \mathbb{Z}_+. \]

Hence, $p_{k+1} \leqslant p_k$ for all $k\in \mathbb {Z}_+$. Since $e-p_k$ is a self-adjoint idempotent, we see that $p_k \leqslant e$ for all $k\in \mathbb {Z}_+.$ This proves (i).

(ii) We can argue as in the second paragraph of the proof of Corollary 8.5 (the arguments given there are purely $C^*$-algebraic).

(iii) The identity $u_k=t^{\prime } p_k t^{\prime *}$ is obvious. It follows from (ii) that $c_k^{-1} \geqslant e$ and $c_k^{-1} \leqslant c_{k+1}^{-1}$ for all $k\in \mathbb {Z}_+$, so

\begin{align*} 0 \leqslant t^{\prime (k+1)} t^{\prime * (k+1)} & \leqslant\mathop{\overbrace{t^{\prime (k+1)} c_k^{{-}1} t^{\prime * (k+1)}}}\limits^{u_k} \\ & \leqslant t^{\prime (k+1)} c_{k+1}^{{-}1} t^{\prime * (k+1)} = p_{k+1} \mathop{\leqslant}\limits^{\mathrm{(i)}} e,\quad k\in \mathbb{Z}_+, \end{align*}

which gives the second part of (iii). The third part of (iii) follows from

\[ u_{k+1} = t^{\prime} p_{k+1} t^{\prime *}\mathop{\leqslant}\limits^{\mathrm{(i)}} t^{\prime} p_k t^{\prime *} = u_k, \quad k \in \mathbb{Z}_+. \]

(iv) It is easy to see that the identity $v_k = p_k t^{\prime *}t^{\prime } p_k$ is valid. Hence, by (i) and (ii), we have

\[ 0 \leqslant v_k = p_k c_1 p_k \leqslant p_k^2=p_k \leqslant e,\quad k \in \mathbb{Z}_+, \]

which proves the third part of (iv). Finally, we come to the conclusion that

\[ v_{k+1} = p_{k+1} (t^{\prime *} t^{\prime}) p_{k+1} \mathop =\limits^{\mathrm{(i)}} p_{k+1} (p_k(t^{\prime *} t^{\prime})p_k) p_{k+1} = p_{k+1} v_k p_{k+1}, \quad k\in \mathbb{Z}_+, \]

which gives the first identity in (iv).

The proof of the ‘moreover’ part is as follows. That $t$ is an expansive element of $C^*(t)$ and $t^{\prime }, c_k, c_k^{-1} \in C^*(t)$ for every $k\in \mathbb {Z}_+$ follows from (9.1) and the fact that $\sigma _{C^*(t)}(s)=\sigma _{\mathcal {C}}(s)$ for every $s \in C^*(t)$ (see [17, Proposition VIII.1.14]; see also [17, Theorem VIII.3.6]). As a consequence, each of the elements $p_k$, $u_k$ and $v_k$ belongs to $C^*(t).$ This completes the proof.

The following property of elements of class $\mathcal {A}_k$ is a direct consequence of Proposition 9.3 and [17, Proposition VIII.1.14]. We will call it $C^*$-permanence property which is shared by some other classes of elements of a unital $C^*$-algebra, including hyponormal ones.

Corollary 9.4 If $\mathcal {C}$ is a unital $C^*$-algebra, $t\in \mathcal {C}$ and $k\in \mathbb {Z}_+,$ then $t$ is of class $\mathcal {A}_k$ if and only if $t$ is of class $\mathcal {A}_k$ as an element of $C^*(t).$

The question of the existence of limits of sequences that were defined in (9.2) is discussed below in the context of $W^*$-algebras. Given an element $t$ of a $W^*$-algebra $\mathcal {W}$, we denote by $W^*(t)$ the $W^*$-algebra generated by $t$ and the unit element of $\mathcal {W},$ that is, $W^*(t)$ is the $\sigma (\mathcal {W}, \mathcal {W}_{*})$-closure of $C^*(t)$, where $\mathcal {W}_{*}$ is the predual of $\mathcal {W}$ (see [34, Corollary 1.7.9]). Recall that every $W^*$-algebra always has a unit (see [34, Sec. 1.7]).

Proposition 9.5 Let $\mathcal {W}$ be a $W^*$-algebra with predual $\mathcal {W}_{*}$ and $t\in \mathcal {W}$ be an expansion. Let $\{p_k\}_{k=0}^{\infty },$ $\{u_k\}_{k=0}^{\infty }$ and $\{v_k\}_{k=0}^{\infty }$ be as in (9.2). Then

1. (i) the sequence $\{p_k\}_{k=0}^{\infty }$ is $\sigma (\mathcal {W}, \mathcal {W}_{*})$-convergent to a projection $($i.e., a self-adjoint idempotent$)$ of $\mathcal {W}$ denoted by $p_{\infty },$

2. (ii) $p_{\infty }$ is the infimum of $\{p_k\}_{k=0}^{\infty }$ computed in the set of all self-adjoint elements of $\mathcal {W}$ $($equivalently, in the set of all projections of $\mathcal {W}),$

3. (iii) the sequences $\{u_k\}_{k=0}^{\infty }$ and $\{v_k\}_{k=0}^{\infty }$ are $\sigma (\mathcal {W}, \mathcal {W}_{*})$-convergent to positive elements of $\mathcal {W}$ denoted by $a$ and $b$, respectively.

Moreover, $t$ is an expansive element of $W^*(t)$ and the elements $t^{\prime }$, $c_k$, $c_k^{-1}$, $p_k$, $u_k,$ $v_k,$ $p_{\infty },$ $a$ and $b$ belong to $W^*(t).$

Proof. (i)&(ii) By Proposition 9.3(i), $\{p_k\}_{k=0}^{\infty }$ is a uniformly bounded monotonically decreasing sequence of projections of $\mathcal {W}.$ It can be deduced from [34, Lemma 1.7.4, Theorem 1.16.7 and Corollary 1.15.6] and [29, Theorem 4.3.5] that the sequence $\{p_k\}_{k=0}^{\infty }$ is $\sigma (\mathcal {W},\mathcal {W}_{*})$-convergent to a projection of $\mathcal {W}$, call it $p_{\infty }$, which is equal to the infimum of $\{p_k\}_{k=0}^{\infty }$ computed in the set of all self-adjoint elements of $\mathcal {W}$. Consequently, $p_{\infty }$ coincides with the infimum of $\{p_k\}_{k=0}^{\infty }$ computed in the set of all projections of $\mathcal {W}$.

(iii) It follows from [34, Theorem 1.16.7] that there exists a faithful $W^*$-representation $\pi \colon \mathcal {W} \to \mathcal {B}(\mathcal {H})$ of $\mathcal {W}.$ By [34, Proposition 1.16.2], $\pi (\mathcal {W})$ is $\sigma (\mathcal {B}(\mathcal {H}),\mathcal {B}(\mathcal {H})_{*})$-closed. In turn, according to [34, Proposition 1.15.1], $\pi (\mathcal {W})$ is SOT-closed. Since $\pi$ is an isometric $W^*$-homomorphism, we deduce from [36, Corollary 1.15.6] that for every $r\in (0,\infty )$, the mapping

\[ \pi_r:=\pi|_{\mathcal{W}_r} \colon \mathcal{W}_r\to \pi(\mathcal{W})_r \]

is continuous if $\mathcal {W}_r$ and $\pi (\mathcal {W})_r$ are equipped with the topologies $\sigma (\mathcal {W}, \mathcal {W}_{*})$ and $\sigma$-WOT (the $\sigma$-weak operator topology), respectively. Because $\pi _r$ is a bijection, we infer from the Banach–Alaoglu theorem that $\pi _r$ is a homeomorphism. By setting $T=\pi (t)$, it can be verified that

(9.5)\begin{equation} \pi(v_k) = T^{\prime k}C_k^{{-}1} C_{k+1} C_k^{{-}1} T^{\prime * k}, \quad k\in \mathbb{Z}_+. \end{equation}

It follows from Proposition 8.7 that $\{\pi (v_k)\}_{k=0}^{\infty }$ converges in SOT, and consequently in $\sigma$-WOT to a positive operator $B\in \mathcal {B}(\mathcal {H})$. Since $\pi (\mathcal {W})$ is SOT-closed, there exists a (unique) positive element $b\in \mathcal {W}$ such that $B=\pi (b).$ By the uniform boundedness principle, there exists $r\in (0,\infty )$ such that $\pi (b), \pi (v_k) \in \pi (\mathcal {W})_r$ for all $k\in \mathbb {Z}_+$. Since $\pi _r$ is a homeomorphism, the sequence $\{v_k\}_{k=0}^{\infty }$ converges in $\sigma (\mathcal {W}, \mathcal {W}_{*})$ to $b$. The same reasoning can be applied to the sequence $\{u_k\}_{k=0}^{\infty }$.

The ‘moreover’ part is a direct consequence of the statements (i) and (iii), the ‘moreover’ part of Proposition 9.3 and [34, Corollary 1.7.9]. This completes the proof.

After this preparation, we can give two equivalent definitions of the class $\mathcal {A}_{\infty }$ in the context of $W^*$-algebras. The first one is patterned on the equivalence (i)$\Leftrightarrow$(iv) of Proposition 8.7.

Definition 9.6 Let $\mathcal {W}$ be a $W^*$-algebra. We say that $t\in \mathcal {W}$ is of class $\mathcal {A}_{\infty }$ if

1. (i) the spectral radius of $t$ is at most $1$,

2. (ii) $t$ is an expansion,

3. (iii) $p_{\infty } ((t^*t)^{-1} - t^{\prime } p_{\infty } t^{\prime *}) p_{\infty } \geqslant 0,$

where $p_{\infty }$ is as in Proposition 9.5.

The second definition is based on the equivalence (i)$\Leftrightarrow$(ii) of Proposition 8.7.

Definition 9.7 Let $\mathcal {W}$ be a $W^*$-algebra. We say that $t\in \mathcal {W}$ is of class $\mathcal {A}_{\infty }$ if

1. (i) the spectral radius of $t$ is at most $1$,

2. (ii) $t$ is an expansion,

3. (iii) $a\leqslant b,$

where $a$ and $b$ are as in Proposition 9.5.

Theorem 9.8 Definitions 9.6 and 9.7 are equivalent.

Proof. Without loss of generality, we can assume that $t$ is an expansive element of $\mathcal {W}.$ Let $\pi \colon \mathcal {W} \to \mathcal {B}(\mathcal {H})$ be a faithful $W^*$-representation of $\mathcal {W}$ (see [34, Theorem 1.16.7]). Set $T=\pi (t)$ and $\mathcal {H}_u'=\bigcap _{n=0}^{\infty }{\mathcal {R}}(T^{\prime n})$. By Proposition 9.5 and [34, Corollary 1.15.6], $\{\pi (p_k)\}_{k=0}^{\infty }$ is $\sigma$-WOT-convergent to $\pi (p_{\infty }).$ Since by (8.1), $\pi (p_k) = P_{{\mathcal {R}}(T^{\prime k})}$ for every $k \in \mathbb {Z}_+,$ we see that $\pi (p_k) \searrow P_{\mathcal {H}_{u}'}$ as $k\nearrow \infty$ in SOT (see the proof of Proposition 8.7). As a consequence,

(9.6)\begin{equation} \pi(p_{\infty}) = P_{\mathcal{H}_{u}'}. \end{equation}

According to the proof of Proposition 9.5(iii), $\{\pi (v_k)\}_{k=0}^{\infty }$ is SOT-convergent to $\pi (b).$ By (9.5), the ‘moreover’ part of Proposition 8.7 and (9.6), we have

(9.7)\begin{equation} \pi(b) = B = P_{\mathcal{H}_{u}'} (T^*T)^{{-}1} P_{\mathcal{H}_{u}'} = \pi(p_{\infty} (t^*t)^{{-}1} p_{\infty}). \end{equation}

The same reasoning applied to the sequence $\{u_k\}_{k=0}^{\infty }$ leads to the identity

(9.8)\begin{equation} \pi(a) = A=P_{\mathcal{H}_{u}'} T^{\prime} P_{\mathcal{H}_{u}'} T^{\prime *} P_{\mathcal{H}_{u}'} = \pi(p_{\infty} t^{\prime} p_{\infty} t^{\prime *} p_{\infty}). \end{equation}

Clearly, the condition (iii) of Definition 9.7 is equivalent to $\pi (b-a) \geqslant 0,$ which by (9.7) and (9.8) is equivalent to the condition (iii) of Definition 9.6. This completes the proof.

The following is the counterpart of Corollary 9.4 for elements of class $\mathcal {A}_{\infty }$.

Corollary 9.9 If $\mathcal {W}$ is a $W^*$-algebra and $t\in \mathcal {W},$ then $t$ is of class $\mathcal {A}_{\infty }$ if and only if $t$ is of class $\mathcal {A}_{\infty }$ as an element of $W^*(t).$

Proof. It follows from Proposition 9.5 and [17, Proposition VIII.1.14] that the infimum of $\{p_k\}_{k=0}^{\infty }$ computed in the set of all projections of $\mathcal {W}$ coincides with the infimum of $\{p_k\}_{k=0}^{\infty }$ computed in the set of all projections of $W^*(t).$ Hence, by Theorem 9.8, we can apply Definition 9.6 and [17, Proposition VIII.1.14] again.

One can see by applying Remark 1.2, Propositions 8.7 and 9.5 and [34, Corollary 1.15.6] that Definitions 7.1 and 9.7 coincide for $k=\infty$ if $\mathcal {W} =\mathcal {B}(\mathcal {H})$. Regarding Proposition 9.5(ii), it is worth pointing out that the property of being closed under the operation of taking infimum is one of the two basic properties characterizing $W^*$-algebras among $C^*$-algebras (cf. [27, Definition 2.1]).