Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T06:01:18.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Unbalanced optimal total variation transport problems and generalized Wasserstein barycenters

Part of: Existence theories Variational problems in infinite-dimensional spaces

Published online by Cambridge University Press:  04 June 2021

Nhan-Phu Chung  and
Thanh-Son Trinh
Nhan-Phu Chung
Affiliation:
Department of Mathematics, Sungkyunkwan University, 2066 Seobu-ro, Jangan-gu, Suwon, Gyeonggi-do 16419, Korea ([email protected]; [email protected]; [email protected])
Thanh-Son Trinh
Affiliation:
Department of Mathematics, Sungkyunkwan University, 2066 Seobu-ro, Jangan-gu, Suwon, Gyeonggi-do 16419, Korea ([email protected]; [email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we establish a Kantorovich duality for unbalanced optimal total variation transport problems. As consequences, we recover a version of duality formula for partial optimal transports established by Caffarelli and McCann; and we also get another proof of Kantorovich–Rubinstein theorem for generalized Wasserstein distance 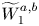$\widetilde {W}_1^{a,b}$ proved before by Piccoli and Rossi. Then we apply our duality formula to study generalized Wasserstein barycenters. We show the existence of these barycenters for measures with compact supports. Finally, we prove the consistency of our barycenters.

Keywords

Unbalanced optimal transportdualitygeneralized Wasserstein spacebarycenter

MSC classification

Primary: 90C46: Optimality conditions, duality
Secondary: 49J40: Variational methods including variational inequalities 58E30: Variational principles
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 674 - 700
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agueh, M. and Carlier, G.. Barycenters in the Wasserstein space. SIAM J. Math. Anal. 43 (2011), 904–924.CrossRefGoogle Scholar
Alibert, J.-J., Bouchitté, G. and Champion, T.. A new class of costs for optimal transport planning. European J. Appl. Math. 30 (2019), 1229–1263.CrossRefGoogle Scholar
Ambrosio, L., Gigli, N. and Savare, G.. Gradient Flows in Metric Spaces and in the Space of Probability Measures, 2nd edn, Lectures in Math (Basel: ETH Zuurich, Birkhauser Verlag, 2008).Google Scholar
Backhoff-Veraguas, J., Beiglböck, M. and Pammer, G.. Existence, duality, and cyclical monotonicity for weak transport costs. Calc. Var. Partial Differential Equations 58 (2019), 1–28.CrossRefGoogle Scholar
Boissard, E., Le Gouic, T. and Loubes, J.-M.. Distribution's template estimate with Wasserstein metrics. Bernoulli 21 (2015), 740–759.CrossRefGoogle Scholar
Caffarelli, L. A. and McCann, R. J.. Free boundaries in optimal transport and Monge-Ampère obstacle. Ann. Math. 171 (2010), 673–730.CrossRefGoogle Scholar
Chizat, L., Peyré, G., Schmitzer, B. and Vialard, F.-X.. Unbalanced optimal transport: dynamic and Kantorovich formulations. J. Funct. Anal. 274 (2018), 3090–3123.CrossRefGoogle Scholar
Chung, N.-P. and Phung, M.-N.. Barycenters in the Hellinger-Kantorovich space. to appear Applied Mathematics & Optimization.Google Scholar
Chung, N.-P. and Trinh, T.-S.. Duality and quotients spaces of generalized Wasserstein spaces. arXiv:1904.12461.Google Scholar
Chung, N.-P. and Trinh, T.-S.. Weak optimal entropy transport problems. arXiv:2101.04986.Google Scholar
Ekeland, I. and Témam, R.. Convex analysis and variational problems. Corrected reprint of the 1976 English edition, Classics in Applied Mathematics, vol. 28 (Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM), 1999). Translated from the French.CrossRefGoogle Scholar
Friesecke, G., Matthes, D. and Schmitzer, B.. Barycenters for the Hellinger-Kantorovich distance over ${{\mathbb {R}}}^{d}$. SIAM J. Math. Anal. 53 (2021), 62–110.CrossRefGoogle Scholar
Gozlan, N., Roberto, C., Samson, P.-M. and Tetali, P.. Kantorovich duality for general transport costs and applications. J. Funct. Anal. 273 (2017), 3327–3405.CrossRefGoogle Scholar
Hanin, L. G.. Kantorovich-Rubinstein norm and its application in the theory of Lipschitz spaces. Proc. Am. Math. Soc. 115 (1992), 345–352.CrossRefGoogle Scholar
Hanin, L. G.. An extension of the Kantorovich norm. Monge Ampère equation: applications to geometry and optimization (Deerfield Beach, FL, 1997), Contemp. Math., vol. 226 (Providence, RI: Am. Math. Soc., 1999), pp. 113–130.Google Scholar
Kitagawa, J. and Pass, B.. The multi-marginal optimal partial transport problem. Forum Math. Sigma. 3 (2015), E17.CrossRefGoogle Scholar
Kondratyev, S., Monsaingeon, L. and Vorotnikov, D.. A new optimal transport distance on the space of finite Radon measures. Adv. Differential Equations 21 (2016), 1117–1164.Google Scholar
Liero, M., Mielke, A. and Savaré, G.. Optimal entropy-transport problems and a new Hellinger-Kantorovich distance between positive measures. Invent. Math. 211 (2018), 969–1117.CrossRefGoogle Scholar
Parthasarathy, K. R.. Probability measures on metric spaces (Providence, RI: AMS Chelsea Publishing, 2005). Reprint of the 1967 original.Google Scholar
Piccoli, B. and Rossi, F.. Generalized Wasserstein distance and its application to transport equations with source. Arch. Ration. Mech. Anal. 211 (2014), 335–358.CrossRefGoogle Scholar
Piccoli, B. and Rossi, F.. On properties of the generalized Wasserstein distance. Arch. Ration. Mech. Anal. 222 (2016), 1339–1365.CrossRefGoogle Scholar
Piccoli, B., Rossi, F. and Tournus, M.. A Wasserstein norm for signed measures, with application to non local transport equation with source term. hal-01665244v3.Google Scholar
Rudin, W.. Real and complex analysis, 3rd edn (New York: McGraw-Hill Book Co., 1987).Google Scholar
Sturm, K.-T.. Probability measures on metric spaces of nonpositive curvature. Heat kernels and analysis on manifolds, graphs, and metric spaces (Paris 2002), Contemp. Math., vol. 338 (Providence, RI, Amer. Math. Soc., 2003), pp. 357–390.Google Scholar
Villani, C.. Topics in optimal transportation. Graduate Studies in Mathematics, vol. 58 (Providence, RI, Amer. Math. Soc., 2003).Google Scholar
Villani, C.. Optimal transport. Old and New. Grundlehren der Mathematischen Wissenschaften (Fundamental Principles of Mathematical Sciences), vol. 338 (Berlin: Springer-Verlag, 2009).CrossRefGoogle Scholar