Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-05T02:41:35.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic generalised KPP equations

Published online by Cambridge University Press:  14 November 2011

I. M. Davies ,
A. Truman  and
H. Z. Zhao
I. M. Davies
Affiliation:
Department of Mathematics, University of Wales Swansea, Singleton Park, Swansea SA2 8PP, U.K.
A. Truman
Affiliation:
Department of Mathematics, University of Wales Swansea, Singleton Park, Swansea SA2 8PP, U.K.
H. Z. Zhao
Affiliation:
Department of Mathematics, University of Wales Swansea, Singleton Park, Swansea SA2 8PP, U.K.
Get access Rights & Permissions [Opens in a new window]

Abstract

We classify multiplicative white noise perturbations k(·) dw, of generalised KPP equations and their effects on deterministic approximate travelling wave solutions by the behaviour of 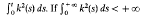, the solutions of the stochastic generalised KPP equations converge to deterministic approximate travelling waves and if

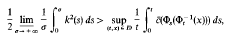
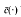being an associated potential energy, Фs a solution of the corresponding classical mechanical equations of Newton, D being a certain domain in R1 × Rr then the white noise perturbations essentially destroy the wave structure and force the solutions to die down.

For the case

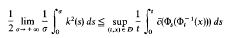
(suppose the existence of the limit) we show that there is a residual wave form but propagating at a different speed from that of the unperturbed equations. Numerical solutions are included and give good agreement with theoretical results.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 5 , 1996 , pp. 957 - 983
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Champneys, A., Harris, S., Toland, J., Warren, J. and Williams, D.. Algebra, analysis and probability for a coupled system of reaction diffusion equations. Philos. Trans. Roy. Soc. London 305 (1995), 69–112.Google Scholar
2Elworthy, K. D.. Stochastic Differential Equations on Manifolds, London Mathematical Society Lecture Notes Series 70 (Cambridge: Cambridge University Press, 1982).Google Scholar
3Elworthy, K. D. and Truman, A.. Classical mechanics, the diffusion (heat) equation and the Schrödinger Equation on a Riemannian manifold. J. Math. Phys. 22 (1981), 2144–66.CrossRefGoogle Scholar
4Elworthy, K. D. and Truman, A.. The diffusion equation and classical mechanics: an elementary formula. In Stochastic Processes in Quantum Physics, eds Albeverio, S. et al. , Lecture Notes in Physics 173, 136–46 (Berlin: Springer, 1982).Google Scholar
5Elworthy, K. D., Truman, A. and Zhao, H. Z.. Approximate travelling waves for the generalized KPP equations and classical mechanics with an appendix by J. G. Gaines. Proc. Roy. Soc. London Ser. A 446 (1994), 529–54.Google Scholar
6Elworthy, K. D. and Zhao, H. Z.. The propagation of travelling waves for stochastic generalized KPP equations. Math. Comput. Modelling 20 (1994), 131–66.Google Scholar
7Elworthy, K. D. and Zhao, H. Z.. Approximate travelling waves for stochastic generalised KPP equations. In Probability Theory and Mathematical Statistics: Proceedings of the Euler Institute Seminars Dedicated to the Memory of Kolmogorov, eds Ibragimov, I. A. and Zaitsev, A. Y., 141–54 (New York: Gordon and Breach, 1995).Google Scholar
8Fisher, R. A.. The wave of advance of advantageous genes. Ann. Eugenics 7 (1937), 353–69.Google Scholar
9Freidlin, M. I.. Functional Integration and Partial Differential Equations (Princeton, NJ: Princeton University Press, 1985).Google Scholar
10Freidlin, M. I.. Semi-linear PDE's and Limit Theorem for Large Deviations, Lecture Notes in Mathematics 1527, 1–109 (Berlin: Springer, 1992).Google Scholar
11Gaines, J. G. (1994). Appendix to [5].Google Scholar
12Gaines, J. G. (1994). Appendix to [6].Google Scholar
13Kloeden, P. E. and Platen, E.. Numerical Solution of Stochastic Differential Equations, Applications of Mathematics 23 (Berlin: Springer, 1992).CrossRefGoogle Scholar
14Kolmogoroff, A., Petrovsky, I. and Piscounoff, N.. Etude de l'equation de la Diffusion Avec Croissance de la Matière et son Application à un Problème Biologique. Moscow Univ. Math. Bull. 1 (1937), 1–25.Google Scholar
15Mueller, C. and Sowers, R.. Travelling waves for the KPP equations with noise. In Stochastic Analysis, Proceedings of Symposia in Pure Mathematics 57, eds Cranston, M. C., Pinsky, M. A., 603–9. (Providence, RI: American Mathematical Society, 1995).Google Scholar
16Tribe, R.. A travelling wave solution to the Kolmogorov equation with noise (Preprint 73, Institut fur Angewandte Analysis und Stochastik, Berlin, 1994).Google Scholar
17Truman, A.. Classical mechanics, the diffusion (heat) equation, and the Schrodinger Equation. J. Math. Phys. 18 (1977), 2308–15.Google Scholar
18Truman, A. and Zhao, H. Z.. The stochastic Hamilton Jacobi theory and related topics. In Stochastic Partial Differential Equations, London Mathematical Society Lecture Note Series 216, ed.Etheridge, A. M., 287–303 (Cambridge: Cambridge University Press, 1995).CrossRefGoogle Scholar
19Varadhan, S. R. S. Diffusion process in a small time interval. Comm. Pure Appl. Math. 20 (1967), 659–85.CrossRefGoogle Scholar
20Zhao, H. Z.. The travelling wave fronts of nonlinear reaction–diffusion systems via Freidlin's stochastic approaches. Proc. Roy. Soc. Edinburgh Sect. A 124 (1994), 273–99.CrossRefGoogle Scholar
21Zhao, H. Z. and Elworthy, K. D.. The travelling wave solutions of scalar generalized KPP equations via classical mechanics and stochastic approaches. In Stochastics and Quantum Mechanics, eds Truman, A. and Davies, I. M., 298–316 (Singapore: World Scientific, 1992).Google Scholar