Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T13:38:27.054Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral properties of a beam equation with eigenvalue parameter occurring linearly in the boundary conditions

Part of: Dynamical problems Ordinary differential operators General theory of linear operators Qualitative theory Boundary value problems

Published online by Cambridge University Press:  30 July 2021

Ziyatkhan S. Aliyev Open the ORCID record for Ziyatkhan S. Aliyev [Opens in a new window]  and
Gunay T. Mamedova Open the ORCID record for Gunay T. Mamedova [Opens in a new window]
Ziyatkhan S. Aliyev
Affiliation:
Baku State University, Baku AZ1148, Azerbaijan Institute of Mathematics and Mechanics NAS of Azerbaijan, Baku AZ1141, Azerbaijan National Aviation Academy of Azerbaijan, Baku AZ1045, Azerbaijan ([email protected])
Gunay T. Mamedova
Affiliation:
Ganja State University, Ganja AZ2001, Azerbaijan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider an eigenvalue problem for ordinary differential equations of fourth order with a spectral parameter in the boundary conditions. The location of eigenvalues on real axis, the structure of root subspaces and the oscillation properties of eigenfunctions of this problem are investigated, and asymptotic formulas for the eigenvalues and eigenfunctions are found. Next, by the use of these properties, we establish sufficient conditions for subsystems of root functions of the considered problem to form a basis in the space 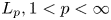$L_p,1 < p < \infty$.

Keywords

Differential operatorEigenvalueEigenfunctionBasis property of root functions

MSC classification

Primary: 34B05: Linear boundary value problems
Secondary: 34B08: Parameter dependent boundary value problems 34C10: Oscillation theory, zeros, disconjugacy and comparison theory 34L10: Eigenfunctions, eigenfunction expansions, completeness of eigenfunctions 47A75: Eigenvalue problems 74H45: Vibrations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 780 - 801
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliyev, Z. S.. On the defect basicity of the system of root functions of differential operators with spectral parameter in the boundary conditions. Proc. Inst. Math. Mech. Natl. Acad. Sci. Azerbaijan 28 (2008), 3–14.Google Scholar
Aliev, Z. S.. Basis properties in $L_p$ of systems of root functions of a spectral problem with spectral parameter in a boundary condition. Differ. Equ. 47 (2011), 766–777.CrossRefGoogle Scholar
Aliev, Z. S.. On basis properties of root functions of a boundary value problem containing a spectral parameter in the boundary conditions. Dokl. Math. 87 (2013), 137–139.CrossRefGoogle Scholar
Aliev, Z. S. and Dunyamalieva, A. A.. Basis properties of root functions of the Sturm-Liouville problem with a spectral parameter in the boundary conditions. Dokl. Math. 88 (2013), 441–445.10.1134/S1064562413030289CrossRefGoogle Scholar
Aliyev, Z. S. and Guliyeva, S. B.. Properties of natural frequencies and harmonic bending vibrations of a rod at one end of which is concentrated inertial load. J. Differ. Equ. 263 (2017), 5830–5845.CrossRefGoogle Scholar
Aliyev, Z. S., Kerimov, N. B. and Mekhrabov, V. A.. On the convergence of expansions in eigenfunctions of a boundary value problem with a spectral parameter in the boundary conditions, I. Differ. Equ. 56 (2020), 143–157.10.1134/S0012266120020019CrossRefGoogle Scholar
Aliyev, Z. S., Kerimov, N. B. and Mekhrabov, V. A.. On the convergence of expansions in eigenfunctions of a boundary value problem with a spectral parameter in the boundary conditions, II. Differ. Equ. 56 (2020), 277–289.CrossRefGoogle Scholar
Aliyev, Z. S. and Mamedova, G. T.. Some properties of eigenfunctions for the equation of vibrating beam with a spectral parameter in the boundary conditions. J. Differ. Equ. 269 (2020), 1383–1400.CrossRefGoogle Scholar
Aliyev, Z. S. and Namazov, F. M.. On the spectral problem arising in the mathematical model of bending vibrations of a homogeneous rod. Complex Anal. Oper. Theory 13 (2019), 3675–3693.CrossRefGoogle Scholar
Aliyev, Z. S. and Namazov, F. M.. Spectral properties of the equation of a vibrating rod at both ends of which the masses are concentrated. Banach J. Math. Anal. 14 (2020), 585–606.CrossRefGoogle Scholar
Altinisik, N., Kadakal, M. and Mukhtarov, O.Sh.. Eigenvalues and eigenfunctions of discontinuous Sturm–Liouville problems with eigenparameter-dependent boundary conditions. Acta Math. Hungar. 102 (2004), 159–193.CrossRefGoogle Scholar
Ben Amara, J. and Vladimirov, A. A.. On a fourth-order problem with spectral and physical parameters in the boundary condition. Izvestiya: Math. 68 (2004), 645–658.CrossRefGoogle Scholar
Ben Amara, J. and Vladimirov, A. A.. On oscillation of eigenfunctions of a fourth-order problem with spectral parameters in the boundary conditions. J. Math. Sci. 150 (2008), 2317–2325.CrossRefGoogle Scholar
Banks, D. O. and Kurowski, G. J.. A Prufer transformation for the equation of a vibrating beam subject to axial forces. J. Differ. Equ. 24 (1977), 57–74.10.1016/0022-0396(77)90170-XCrossRefGoogle Scholar
Binding, P. A., Browne, P. J. and Seddighi, K.. Sturm-Liouville problems with eigenparameter dependent boundary conditions. Proc. Edinburgh Math. Soc. 37 (1994), 57–72.CrossRefGoogle Scholar
Binding, P. A. and Browne, P. J.. Application of two parameter eigencurves to Sturm-Liouville problems with eigenparameter-dependent boundary conditions. Proc. Roy. Soc. Edinburgh Sect. A 125 (1995), 1205–1218.CrossRefGoogle Scholar
Binding, P. A., Browne, P. J. and Watson, B. A.. Sturm-Liouville problems with boundary conditions rationally dependent on the eigenparameter I. Proc. Edinb. Math. Soc. 45 (2002), 631–645.10.1017/S0013091501000773CrossRefGoogle Scholar
Binding, P. A., Browne, P. J. and Watson, B. A.. Sturm-Liouville problems with boundary conditions rationally dependent on the eigenparameter II. J. Comput. Appl. Math. 148 (2002), 147–168.10.1016/S0377-0427(02)00579-4CrossRefGoogle Scholar
Bolotin, B. B.. Vibrations in technique: Handbook in 6 volumes, The vibrations of linear systems, I (Moscow: Engineering Industry, 1978).Google Scholar
Courant, R. and Hilbert, D.. Methods of mathematical physics, I, Interscience, New York, 1953.Google Scholar
Fulton, C. T.. Two-point boundary value problems with eigenvalue parameter in the boundary conditions. Proc. Roy. Soc. Edinburgh, Sect. A 77 (1977), 293–308.CrossRefGoogle Scholar
Gao, C., Li, X. and Ma, R.. Eigenvalues of a linear fourth-order differential operator with squared spectral parameter in a boundary condition. Mediterr. J. Math. 15 (2018), 1–14.CrossRefGoogle Scholar
Gao, C. and Ran, M.. Spectral properties of a fourth-order eigenvalue problem with quadratic spectral parameters in a boundary condition. AIMS Math. 5 (2020), 904–922.CrossRefGoogle Scholar
Hinton, D. B.. An expansion theorem for an eigenvalue problem with eigenvalue parameter in the boundary condition. Quart. J. Math. Oxford 30 (1979), 33–42.CrossRefGoogle Scholar
Ilin, V. A.. Unconditional basis property on a closed interval of systems of eigen- and associated functions of a second-order differential operator. Dokl. Akad. Nauk SSSR 273 (1983), 1048–1053. (in Russian).Google Scholar
Kapustin, N.Yu.. Oscillation properties of solutions to a nonselfadjoint spectral problem with spectral parameter in the boundary condition. Differ. Equ. 35 (1999), 1031–1034.Google Scholar
Kapustin, N.Yu.. On a spectral problem arising in a mathematical model of torsional vibrations of a rod with pulleys at the ends. Diff. Equ. 41 (2005), 1490–1492.CrossRefGoogle Scholar
Kapustin, N. Yu. and Moiseev, E. I.. On the basis property in the space $L_p$ of systems of eigenfunctions corresponding to two problems with spectral parameter in the boundary condition. Diff. Equ. 36 (2000), 1357–1360.Google Scholar
Kerimov, N. B. and Aliev, Z. S.. The oscillation properties of the boundary value problem with spectral parameter in the boundary condition. Trans. Natl. Acad. Sci. Azerb. Ser. Phys.-Tech. Math. Sci. 25 (2005), 61–68.Google Scholar
Kerimov, N. B. and Aliev, Z. S.. On the basis property of the system of eigenfunctions of a spectral problem with spectral parameter in a boundary condition. Differ. Equ. 43 (2007), 905–915.CrossRefGoogle Scholar
Kerimov, N. B. and Poladov, R. G.. Basis properties of the system of eigenfunctions in the Sturm-Liouville problem with a spectral parameter in the boundary conditions. Dokl. Math. 85 (2012), 8–13.CrossRefGoogle Scholar
Mekhrabov, V.A.. Oscillation and basis properties for the equation of vibrating rod at one end of which an inertial mass is concentrated. Math. Meth. Appl. Sci. 44 (2021), 1585–1600.CrossRefGoogle Scholar
Möller, M. and Zinsou, B.. Self-adjoint fourth order differential operators with eigenvalue parameter dependent boundary conditions. Quaest. Math. 34 (2011), 393–406.CrossRefGoogle Scholar
Mukhtarov, O. Sh. and Aydemir, K.. Basis properties of the eigenfunctions of two-interval Sturm-Liouville problems. Anal. Math. Phys. 9 (2019), 1363–1382.CrossRefGoogle Scholar
Naimark, M. A.. Linear differential operators, Ungar, New York, 1967.Google Scholar
Russakovskii, E. M.. Operator treatment of boundary problems with spectral parameters entering via polynomials in the boundary conditions. Funct. Anal. Appl. 9 (1975), 358–359.CrossRefGoogle Scholar
Schneider, A.. A note on eigenvalue problems with eigenvalue parameter in the boundary conditions. Math. Z. 136 (1974), 163–167.CrossRefGoogle Scholar
Shkalikov, A. A.. Boundary value problems for ordinary differential equations with a parameter in the boundary conditions. J. Soviet Math. 33 (1986), 1311–1342.CrossRefGoogle Scholar
Tretter, C.. Boundary eigenvalue problems for differential equations $N \eta = \lambda P \eta$ with $\lambda$-polynomial boundary conditions. J. Differ. Equ. 170 (2001), 408–471.CrossRefGoogle Scholar
Walter, J.. Regular eigenvalue problems with eigenvalue parameter in the boundary condition. Math. Z. 133 (1973), 301–312.CrossRefGoogle Scholar