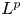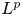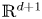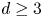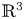Sharp Sobolev regularity of restricted X-ray transforms

Abstract

We study $L^p$-Sobolev regularity estimates for the restricted X-ray transforms generated by nondegenerate curves. Making use of the inductive strategy in the recent work by the authors, we establish the sharp $L^p$-regularity estimates for the restricted X-ray transforms in $\mathbb {R}^{d+1}$, $d\ge 3$. This extends the result due to Pramanik and Seeger in $\mathbb {R}^3$.

1. Introduction

Let $\gamma$ be a smooth curve from $I=[-1,1]$ to $\mathbb {R}^{d}$. We consider

\[ \mathfrak R f(x,s)=\psi(s)\int f(x+t\gamma(s),t)\chi(t)\,{\rm d}t, \quad f\in \mathcal{S}(\mathbb{R}^{d+1}), \]

where $\psi$ and $\chi$ are smooth functions supported in the interiors of the intervals $I$ and $[1,2]$, respectively. The operator $\mathfrak Rf$ is referred to as the restriction of X-ray transform to the line complex generated by the directions $(\gamma (s),1)$, $s \in \operatorname {supp} \psi$. We say $\gamma$ is nondegenerate if

(1.1)\begin{equation} \det( \gamma'(s), \dots, \gamma^{(d)}(s) )\neq0, \quad \forall s\in I. \end{equation}

The operator $\mathfrak Rf$ is a model case of the general class of restricted X-ray transforms (see [12, 16–19]). Especially in $\mathbb {R}^3$, under the nondegeneracy assumption (1.1), $\mathfrak Rf$ is a typical example of Fourier integral operators with one-sided fold singularity [13]. Regularity properties of $\mathfrak Rf$ have been studied in terms of $L^p$ improving and $L^p$ Sobolev regularity estimates. The $L^p$ improving property of $\mathfrak R$ is well understood by now [14, 15, 24, 25]. The problem was, in fact, considered in a more general framework: $L^p-L^q(L^r)$ estimates for $\mathfrak R$ were studied by some authors (see, e.g. [7, 11, 34]) and the estimates on the optimal range of $p,q,r$ were established except for some endpoint cases. (See also [8–10, 20, 33] for related results.)

$L^2-L_{1/(2d)}^2$ bound on $\mathfrak R$ is easy to obtain via $TT^*$ argument and van der Corput's lemma [16] (see also [13, 19] for the sharp $L^2$ Sobolev estimates for general class of operators). Interpolation between this and the trivial $L^\infty$ estimate shows that $\mathfrak R$ is bounded from $L^p$ to $L_{1/(pd)}^p$ for $p\ge 2$. This is optimal in that $L^p-L_{\alpha }^p$ estimate fails if $\alpha > 1/(pd)$ (see Proposition 5.1). However, when $p< 2$, the sharp $L^p$ regularity estimate is less straightforward. Such an estimate has not known until recently. When $d=2$, the optimal $L^p-L_{1/p'}^p$ estimate was established for $1< p<4/3$ by Pramanik and Seeger's conditional result [31] and the sharp decoupling inequality for the cone $\subset \mathbb {R}^3$ due to Bourgain and Demeter [5]. Those estimates and interpolation give the sharp $L^p-L_{1/(2d+)}^p$ estimate for $4/3\le p<2$, but the endpoint $L^p-L_{1/(2d)}^p$ estimate remains open. (See Conjecture 1.1.) In $\mathbb {R}^3$ the result has been extended to more general operators. In fact, Pramanik and Seeger [30] obtained the sharp $L^p$ regularity estimates for the Fourier integral operator with folding canonical relation. Bentsen [4] (also see [3]) extended the result to a class of radon transforms with fold and blowdown singularities.

However, in higher dimensions ($d\ge 3$) the sharp $L^p$ regularity estimates for $\mathfrak R$ have remained open for $1< p<2$. Set $p_d=2d/(2d-1)$ and

\[ \alpha(p)= \begin{cases} 1-\frac 1p, & 1\le p< p_d, \\ \frac 1{2d}, & \ p_d \le p\le 2. \end{cases} \]

It is natural to conjecture the following.

Conjecture 1.1 Let $d\ge 3$ and $1< p < 2$. Suppose $\gamma$ is a smooth nondegenerate curve. Then, $\mathfrak R$ boundedly maps $L^p$ to $L_\alpha ^p$ for $\alpha \le \alpha (p)$.

Failure of $L^p-L_\alpha ^p$ boundedness for $\alpha > \alpha (p)$ can be shown by a slight modification of the examples in [31]. (See Proposition 5.1.) The following is our main result which verifies the conjecture except for some endpoint cases in every dimension $d\ge 3$.

Theorem 1.2 Let $d\ge 3$ and $1\le p< p_d$. Suppose $\gamma$ is nondegenerate. Then,

(1.2)\begin{equation} \|\mathfrak R f\|_{L^p_{\alpha}}\le C\|f\|_{p} \end{equation}

holds if and only if $\alpha \le 1-1/p$.

When $p \in [p_d,2)$, interpolation with the $L^2-L_{1/(2d)}^2$ estimate yields (1.2) for $\alpha <\alpha (p)$ but estimate (1.2) with the endpoint regularity $\alpha =\alpha (p)$, which looks to be a subtle problem, remains open. By a standard scaling argument [29, 31] the result in Theorem 1.2 can be extended to the curves of finite type.

A curve $\gamma : I \mapsto \mathbb {R}^{d}$ is said to be of finite type if there is an $L=L(s)$ such that $\operatorname {span} \{ \gamma ^{(1)}(s), \dots, \gamma ^{(L)}(s)\}=\mathbb {R}^d$ for each $s\in I$, and the smallest of such $L(s)$ is called the type at $s$. The supremum of the type over $s \in I$ is called the maximal type of $\gamma$ (see, e.g. [21, 29]).

Corollary 1.3 Let $d\ge 3$, $1\le p<2$ and $L>d$. Suppose $\gamma$ is a curve of maximal type $L$. Then, $\mathfrak Rf$ is bounded from $L^p$ to $L_\alpha ^p$ for $\alpha \le \min ( \alpha (p), 1/(Lp))$ if $p\neq (L+1)/L$ when $L\ge 2d-1$, and if $p \in (1,p_d) \cup (2d/L,2)$ when $d< L <2d-1$.

For $p\in [2,\infty ]$, it is easy to show the sharp $L^p - L_{1/(Lp)}^p$ estimate, which can be shown by using the $L^2-L_{1/(2L)}^2$ estimate and interpolation in a similar manner as above. Corollary 1.3 and Proposition 5.1 give the optimal Sobolev regularity estimate for $\mathfrak R$ if $L\ge 2d-1$ when $p \neq (L+1)/L$. However, some endpoint cases remain open not to mention such estimates for the nondegenerate curves.

In this paper, we make use of the inductive strategy in the recent work of the authors [23], where smoothing properties of the (convolution) averaging operator over curves were studied (see [2, 22, 26, 27, 32] for previous works). Exploiting similarity between $\mathfrak R^\ast f$ and the averaging operator, we adapt our previous argument. The main new feature of the current paper is use of the decoupling inequality associated with the conical sets generated by curves (see Definition 2.5 and Theorem 3.1). Compared with our previous work where the averaging operator was decoupled by a class of symbols adjusted to short subcurves, our new decoupling inequality allows us to dispense with some technicalities related to the symbols. The decoupling inequality can also be used to simplify the argument in [23].

Organization. In § 2, we reduce the proof of Theorem 1.2 to obtain Proposition 2.4. We prove a decoupling inequality associated with a nondegenerate curve (Theorem 3.1) in § 3 which is crucial for the proof of Proposition 2.4. The proofs of Proposition 2.4 and Theorem 1.2 are given in § 4 and § 5, respectively. We discuss the sharpness of the smoothing order $\alpha$ in § 5.

Notation. For positive constants $A, D$, we denote $A\lesssim D$ if there exists a (independent) constant $C$ such that $A\le CD$, where the constant $C$ may vary from line to line depending on the context.

2. Estimates with localized frequency

In this section, we reduce the proof of Theorem 1.2 to show an inductive statement (see Proposition 2.4). Afterwards, we obtain some preliminary results which are needed to prove Proposition 2.4.

Let us consider the operator

\[ \mathcal{R} f(x,t)=\chi(t)\int f(x-t\gamma(s),s)\psi(s)\,{\rm d}s, \]

which is the dual operator of $\mathfrak R$. By duality estimate (1.2) is equivalent to

(2.1)\begin{equation} \| \mathcal{R}f\|_{L^p(\mathbb{R}^{d+1})} \lesssim \|f\|_{L_{{-}1/p}^p}, \quad 2d< p<\infty. \end{equation}

For the purpose, we closely follow the line of arguments in our previous paper [23]. So, there is a significant overlap between the current paper and [23]. This can be avoided by omitting some shared details. However, we decide to include them so that the paper is self-contained and more easily accessible.

2.1 Frequency localized estimate

We begin with defining a class of curves in order to prove (2.1) in an inductive manner. For an integer $1 \le L \le d$, by ${\rm Vol} (v_1,\ldots,v_L)$ we denote the $L$-dimensional volume of the parallelepiped generated by vectors $v_1,\ldots, v_L \in \mathbb {R}^d$.

Definition 2.1 Let $B\ge 1$. We say $\gamma \in \mathfrak V^d(L,B)$ if $\gamma \in C^{3d+1}(I)$ satisfies

(2.2)\begin{align} & \max_{s\in I} |\gamma^{(j)}(s)|\,\le\, B, \quad 0\le j\le 3d+1, \end{align}

(2.3)\begin{align} & \min_{s\in I} {\rm Vol} \left( \gamma^{(1)}(s),\ldots, \gamma^{(L)}(s) \right) \ge B^{{-}1}. \end{align}

For a smooth function $a(s,t,\xi )$ on $I \times [1,2] \times \mathbb {R}^d$, we define

\[ \mathcal{R}[a]f(x,t)=(2\pi)^{{-}d}\iint {\rm e}^{i(x-t\gamma(s))\cdot\xi}a(s,t,\xi) \,\mathcal{F}_x f (\xi,s)\,{\rm d}s\,{\rm d}\xi. \]

Here, $\mathcal {F}_x$ denotes Fourier transform in $x$. Note that $\mathcal {R}f =\mathcal {R}[a]f$ if $a(s,t,\xi )=\psi (s)\chi (t)$. We prove estimate (2.1) by induction on $L$ for $\gamma \in \mathfrak V^d(L,B)$ under the localized nondegeneracy assumption:

(2.4)\begin{equation} \sum_{\ell=1}^L |\langle \gamma^{(\ell)}(s), \xi\rangle| \ge B^{{-}1}|\xi| \end{equation}

which holds if $(s,t,\xi ) \in \operatorname {supp} a$ for some $t$. When $L< d$, (2.4) cannot be true in general even if $\gamma$ is nondegenerate. However, an appropriate decomposition in the frequency domain makes it possible that (2.4) holds. To do this, we consider a class of symbols $a$.

Definition 2.2 Let $\mathbb {A}_k=\{ \xi \in \mathbb {R}^d: 2^{k-1} \le |\xi | \le 2^{k+1}\}$ for $k\ge 0$, and $\mathcal {I}_L=\{(j,\alpha ): 0 \le j \le 2L, |\alpha | \le d+L+2\}$. We say a symbol $a\in C^{d+L+2}(\mathbb {R}^{d+2})$ is of type $(2^k,L,B)$ if $\operatorname {supp} a \subset I \times [2^{-1},2^2]\times \mathbb {A}_k$

\[ |\partial_t^{j}\partial_\xi^\alpha a(s,t,\xi)| \le B |\xi|^{-|\alpha|}, \quad (j,\alpha) \in \mathcal{I}_L, \]

and (2.4) holds on $\operatorname {supp}_{s,\xi } a$. Here, as in [23], we denote $\operatorname {supp}_{s,\xi } a=\cup _{t} \operatorname {supp} a(\cdot,t,\cdot )$. We simply say a statement $S(s,\xi )$, depending on $s,\xi$, holds on $\operatorname {supp} a$ if $S(s,\xi )$ holds for $s,\xi \in \operatorname {supp}_{a,\xi } a$. We also use the same convention with other variables.

Estimate (2.1) (and hence Theorem 1.2) follows from the next theorem via a standard argument using Fefferman–Stein $\#$-function (e.g. see [28]). See § 5.1 for details.

Theorem 2.3 Suppose that $\gamma \in \mathfrak V^d(L,B)$ and $a$ is a symbol of type $(2^k,L,B)$. Then, for $p> 2L$

(2.5)\begin{equation} \| \mathcal{R}[a]f\|_{p}\le C 2^{-k/p}\|f\|_p. \end{equation}

As mentioned above, we prove Theorem 2.3 by induction on $L$. Theorem 2.3 with $L=1$ is easy to prove. Indeed, setting $\tilde {\mathcal {R}}f=\mathcal {F}_x(\mathcal {R}[a] \mathcal {F}_x^{-1}\!f)$, we note that

\[ \tilde{\mathcal{R}}^*\tilde{\mathcal{R}}f(\xi,s)=\int \mathcal{K}(s,s',\xi)f(\xi,s')\,{\rm d}s', \]

where

\[ \mathcal{K}(s,s',\xi)=\int {\rm e}^{it(\gamma(s)-\gamma(s'))\cdot \xi} \overline a(s,t,\xi) a(s',t,\xi)\,{\rm d}t. \]

Since (2.4) holds with $L=1$ on $\operatorname {supp} a$, integration by parts gives $|\mathcal {K}(s,s',\xi )| \le C (1+2^k|s-s'|)^{-2}.$ By Young's convolution inequality it follows that $\|\tilde {\mathcal {R}}^* \tilde {\mathcal {R}}f \|_2 \lesssim 2^{-k}\|f\|_2$. Thus, we get $\| \mathcal {R}[a]f\|_2 \lesssim 2^{-k/2}\|f\|_2$ by Plancherel's theorem. Interpolation with the trivial estimate $\| \mathcal {R}[a]f\|_\infty \lesssim \|f\|_\infty$ gives (2.5) with $L=1$.

Consequently, Theorem 2.3 for $L\ge 2$ follows from the next proposition (cf. [23, Proposition 2.3]).

Proposition 2.4 Let $2 \le N \le d$. Suppose Theorem 2.3 holds with $L=N-1$. Then, Theorem 2.3 holds with $L=N$.

We prove the proposition through the rest of this section, § 3 and § 4. Fixing $2\le N\le d$, we assume that Theorem 2.3 holds with $L=N-1$. Additionally, assuming that $\gamma \in \mathfrak V^d(N,B)$ and $a$ is of type $(2^k,N,B)$, we prove (2.5) for $p>2N$. For the purpose, composing the symbol $a$, we may further assume that

(2.6)\begin{equation} |\gamma^{(N)}(s)\cdot\xi|\ge (2B)^{{-}1}|\xi| \end{equation}

holds on $\operatorname {supp} a$. Otherwise, (2.4) holds with $L=N-1$, so the hypothesis (Theorem 2.3 with $L=N-1$) yields (2.5) for $p> 2(N-1)$.

We prove Proposition 2.4 in § 4 using the associated decoupling inequality which is obtained in § 3. The rest of the section is devoted to proving two lemmas (2.6 and 2.8) which play crucial roles in proving Proposition 2.4.

2.2 Symbols adapted to $\gamma$

We define a class of symbols adapted to the curve $\gamma$. From now on, we assume that $\delta$ satisfies

(2.7)\begin{equation} 2^{{-}k /N}\le \delta \le (2^2B)^{{-}N}. \end{equation}

Let $\gamma$ satisfy (2.3) with $L=N-1$. For $s\in I$, set $\mathrm V_s^{\gamma,\ell } = \operatorname {span} \{\gamma ^{(j)}(s) : j=1,\dots,\ell \}$. Consider a linear map $\tilde {\mathcal {L}}_s^\delta :\mathbb {R}^d \mapsto \mathbb {R}^d$ given as follows:

\begin{align*} (\tilde{\mathcal{L}}_{s}^\delta)^\intercal \gamma^{(j)}(s) & =\delta^{N-j}\gamma^{(j)}(s), \quad j=1,\dots,N-1, \\ (\tilde{\mathcal{L}}_{s}^\delta)^\intercal v & =v, \quad v\in \left(\mathrm V_s^{\gamma,N-1}\right)^{{\perp}}. \end{align*}

We also consider a linear map $\mathcal {L}_s^\delta : \mathbb {R}^{d+1} \mapsto \mathbb {R}^{d+1}$ given by

\[ \mathcal{L}_{s}^\delta(\tau, \xi)= \left(\delta^N \tau - \gamma(s)\cdot \tilde{\mathcal{L}}_s^\delta \xi,\, \tilde{\mathcal{L}}_s^\delta \xi\right), \quad (\tau,\xi)\in \mathbb{R} \times \mathbb{R}^d. \]

Denoting $G(s)=(1,\gamma (s))$, we set

\[ \Lambda_k(\delta,s)=\bigcap_{0\le j\le N-1}\left\{(\tau,\xi) \in \mathbb{R} \times \mathbb{A}_k : |\langle G^{(j)}(s),(\tau,\xi)\rangle| \le B2^{k+5} \delta^{N-j}\right\}, \]

which roughly corresponds to the Fourier support of the operator $\mathcal {R}[a]f$ with $\operatorname {supp}_s a$ included in an interval centred at $s$ of length about $\delta$. We define a class of symbols associated with $\Lambda _k(\delta,s)$.

Definition 2.5 Let $s_{\circ } \in (-1,1)$ and $0<\delta \le 1$ such that $I(s_{\circ },\delta ):=[s_{\circ }-\delta, s_{\circ }+\delta ]\subset I$. We denote by $\mathfrak A_k(\delta,s_{\circ })=\mathfrak A_k(\delta, s_{\circ },d,N,B,\gamma )$ the set of smooth functions $\mathfrak a$ on $\mathbb {R}^{d+3}$ which satisfies the following $:$

(2.8)\begin{align} & \operatorname{supp} \mathfrak a \subset I(s_{{\circ}},\delta)\times [1,2]\times \Lambda_k(\delta,s_{{\circ}}), \end{align}

(2.9)\begin{align} & \left|\partial^{j}_t\partial^{\alpha}_{\tau, \xi} \mathfrak a\left( s,t, \mathcal{L}_{s_{{\circ}}}^\delta(\tau,\xi) \right) \right|\le B|(\tau,\xi)|^{-|\alpha|}, \quad (j,\alpha ) \in \mathcal{I}_N. \end{align}

It should be noted that there is no $s$-differentiation in (2.9). Here, $\mathcal {I}_N$ is given in Definition 2.2. We set

(2.10)\begin{equation} \mathcal{F}(\mathcal{T} [\mathfrak a] f)(\xi,\tau) =\iint {\rm e}^{{-}it'(\tau+ \gamma(s)\cdot \xi)}\mathfrak a(s,t',\tau,\xi)\,{\rm d}t' \, \mathcal{F}_x f (\xi,s)\,{\rm d}s. \end{equation}

Clearly, $\mathcal {R}[a]f=\mathcal {T}[a]f$ if $\mathfrak a=a(s,t,\xi )$. The following is an analogue of [23, Lemma 2.7].

Lemma 2.6 Let $\tilde \chi \in \mathrm C_0^\infty ((2^{-2},2^2))$ such that $\tilde \chi =1$ on $[3^{-1},3]$. Let $\mathfrak a$ be a smooth function which satisfies (2.8) and (2.9) with $j\le 2$ and $|\alpha | \le d+3$. Then, we have

(2.11)\begin{equation} \| \mathcal{T}[\mathfrak a]f\|_{p} \le C\delta^{1- 1/p} \|f\|_p \end{equation}

for $p\ge 2$, and

(2.12)\begin{equation} \|(1-\tilde\chi(t)) \mathcal{T}[\mathfrak a]f\|_{p} \le C\delta^{1- 1/p-N}2^{{-}k} \|f\|_p, \quad p>1. \end{equation}

Proof. Note that $\mathcal {T}[\mathfrak a]f (x,t) = \int K[\mathfrak a](s,t, \cdot )\ast f(\cdot,s)(x)\,{\rm d}s$ where

\[ K[\mathfrak a](s,t,x)=\frac1{ (2\pi)^{d+1}} \iiint {\rm e}^{i(t-t')\tau+i(x-t'\gamma(s))\cdot \xi}\mathfrak a(s,t',\tau,\xi)\,{\rm d}\xi\,{\rm d}\tau\,{\rm d}t'. \]

It is easy to show that $|(\mathcal {L}_{s_{\circ }}^\delta )^{-1} \mathcal {L}_s^\delta (\tau,\xi )| \sim |(\tau,\xi )|$ provided $|s-s_{\circ }| \le \delta$ (cf. [23, Lemma 2.6]). Since (2.8) and (2.9) hold with $j=0$ and $|\alpha | \le d+3$, it follows that $\operatorname {supp} \mathfrak a(s,t,2^k\mathcal {L}_s^\delta \cdot ) \subset \{(\tau,\xi ):|(\tau,\xi )| \lesssim 1\}$ and $|\partial _{\tau,\xi }^\alpha ( \mathfrak a(s,t,2^k\mathcal {L}_s^\delta (\tau,\xi )))| \lesssim 1$, $|\alpha | \le d+3$. By changing variables $(\tau,\xi ) \rightarrow 2^k\mathcal {L}_{s}^\delta (\tau,\xi )$ followed by repeated integration by parts, we have

\begin{align*} & |K[\mathfrak a](s,t,x)| \lesssim \delta^{ {N(N+1)}/2}2^{k(d+1)} \!\int_1^2 \bigl(1+2^k|(\delta^N(t-t'),(\tilde{\mathcal{L}}_{s}^\delta)^\intercal(x-t\gamma(s)))|\bigr)^{{-}d-3}\,{\rm d}t'. \end{align*}

This gives $\|K[\mathfrak a](s,t,\cdot )\|_{L^1_x}\lesssim 1$. From (2.8), note $\mathcal {T}[\mathfrak a]f (x,t) = \int _{I(s_{\circ },\delta )} K[\mathfrak a](s,t, \cdot )\ast f(\cdot,s)(x)\,{\rm d}s$. Thus, we get

\[ \| \mathcal{T}[\mathfrak a]f\|_{\infty} \le C\delta \|f\|_\infty. \]

Recall (2.10). By Plancherel's theorem, integration by parts in $t'$, and Hölder's inequality, we get

\[ \| \mathcal{T} [\mathfrak a] f\|_2^2 \lesssim \delta \int_{I(s_{{\circ}},\delta)}\, \| \mathcal{F}_x f({\cdot}, s) \|_2^2 \,{\rm d}s \lesssim \delta \|f\|_2^2. \]

Thus, interpolation gives (2.11). To show (2.12), we note from the above estimate for $K[\mathfrak a](s,t,x)$ that $\|(1-\tilde \chi (t))K[\mathfrak a](s,t,\cdot )\|_{L^1_x}\lesssim \mathfrak K(t)=: 2^{-k} \delta ^{-N} |t-1|^{-1}(1-\tilde \chi (t))$. By (2.8), using Hölder's and Young's convolution inequalities, as before, we see that $\|(1-\tilde \chi )\mathcal {T}[\mathfrak a]f\|_p^p$ is bounded above by constant times

\[ \delta^{p-1} \int \mathfrak K^p(t) \int_{I(s_{{\circ}},\delta)} \|f({\cdot},s)\|_{L^p_x}^p\,{\rm d}s\,{\rm d}t \lesssim C\delta^{p-1-pN}2^{{-}pk} \|f\|_p^p. \]

This gives (2.12).

2.3 Rescaling

Let $I(s_{\circ },\delta )\subset I$. For $\gamma \in \mathfrak V^d(N,B)$ we consider a rescaled curve

\[ \gamma_{s_{{\circ}}}^\delta(s):=\delta^{{-}N}(\tilde {\mathcal{L}}_{s_{{\circ}}}^\delta)^\intercal \left(\gamma(\delta s+s_{{\circ}})-\gamma(s_{{\circ}})\right). \]

Lemma 2.7 Let $\gamma \in \mathfrak V^d(N,B)$. If $0<\delta <\delta _\ast$ for a $\delta _\ast$ small enough, $\gamma _{s_{\circ }}^\delta \in \mathfrak V^d(N,3 B)$ and $\gamma _{s_{\circ }}^\delta \in \mathfrak V^d(N-1,B')$ for some $B'$.

Proof. Taylor series expansion of $\gamma ^{(j)}(\delta s+s_{\circ })$ at $s=0$ yields:

\[ (\gamma_{s_{{\circ}}}^\delta)^{(\ell)}(s)=\sum_{0\le j \le N-1-\ell} \gamma^{(\ell+j)}(s_{{\circ}})\frac{s^j}{j!}+(\tilde{\mathcal{L}}_{s_{{\circ}}}^\delta )^{\intercal} \gamma^{(N)}(s_{{\circ}}) \frac{s^{N-\ell}}{(N-\ell)!} +O(B\delta) \]

for $1 \le \ell \le N-1$ and $(\gamma _{s_{\circ }}^\delta )^{(N)}(s)=(\tilde {\mathcal {L}}_{s_{\circ }}^\delta )^{\intercal } \gamma ^{(N)}(s_{\circ })+O(B\delta )$. Writing $\gamma ^{(N)}(s_{\circ })=v_1+v_2 \in \mathrm V_{s_{\circ }}^{\gamma,N-1} \oplus (\mathrm V_{s_{\circ }}^{\gamma,N-1})^\perp$, we have $(\tilde {\mathcal {L}}_{s_{\circ }}^\delta )^{\intercal } \gamma ^{(N)}(s_{\circ })=(\tilde {\mathcal {L}}_{s_{\circ }}^\delta )^{\intercal } v_1+v_2=v_2+O(B\delta )$. Since $\gamma \in \mathfrak V^d(N,B)$, we see $\gamma _{s_{\circ }}^\delta \in \mathfrak V^d(N,3B)$ if $0<\delta <\delta _\ast$ for a sufficiently small $\delta _\ast >0$. Consequently, $\gamma _{s_{\circ }}^\delta \in \mathfrak V^d(N-1,B')$ for some $B'$.

The following lemma, which is an analogue of [23, Lemma 2.8], is important for our inductive argument. Let us set

\[ \mathcal{R}[\gamma_{s_{{\circ}}}^{\delta},a]f(x,t)=(2\pi)^{{-}d}\iint {\rm e}^{i(x-t\gamma_{s_{{\circ}}}^{\delta}(s))\cdot\xi}a(s,t,\xi) \mathcal{F}_x f (\xi,s)\,{\rm d}s\,{\rm d}\xi. \]

Lemma 2.8 Let $s_{\circ } \in (-1,1)$, $\mathfrak a \in \mathfrak A_k(\delta,s_{\circ })$, and $\gamma \in \mathfrak V^d(N,B)$. Suppose

(2.13)\begin{equation} \sum_{j=1}^{N-1}\, \delta^{j} |\langle \gamma^{(j)}(s), \xi \rangle |\ge B^{{-}1}2^k \delta^N \end{equation}

for $(s,\xi )\in I(s_{\circ },\delta )\times \operatorname {supp}_\xi \mathfrak a$. Then, there exist constants $C$, $\tilde B$, $\delta _{*}=\delta _{*}(B,N,d)$, and $\tilde f$ and a symbol $\tilde a$ such that

(2.14)\begin{equation} \| \tilde \chi(t) \mathcal{T}[\mathfrak a]f \|_p=\delta^{1- 1/p} \| \mathcal{R}[\gamma_{s_0}^\delta,\tilde a]\tilde f\|_p \end{equation}

for $0<\delta <\delta _{*}$, $\|\tilde f\|_p=\|f\|_p$, $|\partial _t^j\partial _\xi ^\alpha \tilde a(s,t,\xi )| \le \tilde B|\xi |^{-|\alpha |}$ for $(j,\alpha )\in \mathcal {I}_{N-1}$, and

(2.15)\begin{equation} \operatorname{supp} \tilde a \subset I\times [2^{{-}2},2^2]\times \{\xi \in \mathbb{R}^d: C^{{-}1}\delta^N2^k\le |\xi| \le C \delta^N2^k\}. \end{equation}

Proof. Let $\mathfrak a_\delta (s,t,\tau,\xi )=\mathfrak a(\delta s+s_{\circ },t,\tau,\xi )$. By Fourier inversion and (2.10), changing variables $s\rightarrow \delta s+s_{\circ }$, $(\tau,\xi )\rightarrow (\tau -\gamma (s_{\circ })\cdot \xi, \xi )$ gives

(2.16)\begin{equation} \mathcal{T}[\mathfrak a]f(x,t)=(2\pi)^{{-}d}\delta \iint {\rm e}^{i\langle x-t\gamma(s_{{\circ}}),\xi \rangle} b(s,t,\xi) \mathcal{F}_xf(\xi, \delta s+s_{{\circ}})\,{\rm d}s\,{\rm d}\xi, \end{equation}

where

\[ b(s,t,\xi)= \frac{1}{2\pi}\iint {\rm e}^{it\tau}\,{\rm e}^{{-}it' ( \tau+ \langle \gamma(\delta s+s_{{\circ}})-\gamma(s_{{\circ}}), \xi \rangle)} \mathfrak a_\delta\left(s, t', \tau-\gamma(s_{{\circ}})\cdot \xi, \xi\right)\,{\rm d}t'\,{\rm d}\tau. \]

We observe that

\[ \tilde \chi(t) b(s,t, \delta^{{-}N}\tilde{\mathcal{L}}_{s_{{\circ}}}^\delta \xi) = {\rm e}^{{-}it\gamma_{s_{{\circ}}}^\delta (s)\cdot \xi}\, \tilde a(s,t,\xi), \]

where

(2.17)\begin{equation} \tilde{ a}(s,t,\xi)=\frac 1{2\pi}\iint\,{\rm e}^{{-}it'(\tau+\gamma_{s_{{\circ}}}^\delta(s)\cdot \xi)}\tilde{\chi}(t)\mathfrak a_\delta(s,t'+t,\delta^{{-}N}\mathcal{L}_{s_{{\circ}}}^\delta(\tau,\xi))\,{\rm d}t'\,{\rm d}\tau. \end{equation}

It is clear that (2.15) holds for some $C\ge 1$. Since $\mathfrak a \in \mathfrak A_k(\delta,s_{\circ })$, it is not difficult to see $|\partial _t^j \partial _\xi ^\alpha \tilde a(s,t,\xi )| \le \tilde B |\xi |^{-|\alpha |}$ for $(j,\alpha ) \in \mathcal {I}_{N-1}$ (see (2.25) in [23]).

Set $\mathcal {C}_p=\mathcal {C}_p(\delta ):= \delta ^{1/p} |\det \delta ^{-N} \tilde {\mathcal {L}}_{s_{\circ }}^\delta |^{1-1/p}$. Let $\tilde f$ be given by $\mathcal {F}_x \tilde f (\xi,s)= \mathcal {C}_p \mathcal {F}_x f( \delta ^{-N} \tilde {\mathcal {L}}_{s_{\circ }}^\delta \xi, \delta s+s_{\circ })$, thus $\|\tilde f\|_p=\|f\|_p$. Recalling (2.16) and changing variables $\xi \rightarrow \delta ^{-N} \tilde {\mathcal {L}}_{s_{\circ }}^\delta \xi$, we now have

\[ \tilde \chi(t) \mathcal{T}[\mathfrak a]f(x,t) = \frac{\mathcal{C}_{p'}}{(2\pi)^{d}} \iint {\rm e}^{i \langle x-t\gamma(s_{{\circ}}), \delta^{{-}N}\tilde{\mathcal{L}}_{s_{{\circ}}}^\delta \xi \rangle}\,{\rm e}^{{-}it\gamma_{s_{{\circ}}}^\delta (s)\cdot \xi} \,\tilde a(s,t,\xi) \mathcal{F}_x \tilde f(\xi,s)\,{\rm d}s\,{\rm d}\xi. \]

This gives $\tilde \chi (t)\mathcal {T} [\mathfrak a]f(x,t) =\mathcal {C}_{p'} \mathcal {R}[\gamma _{s_{\circ }}^\delta,\tilde a] \tilde f ( y,t)$ where $y=\delta ^{-N} ( \tilde {\mathcal {L}}_{s_{\circ }}^\delta )^{\intercal } (x-t\gamma (s_{\circ }))$. Therefore, changing variable $x \rightarrow \delta ^{N} (\tilde {\mathcal {L}}_{s_{\circ }}^\delta )^{-\intercal }x+t\gamma (s_{\circ })$, we obtain (2.14).

Combining Lemma 2.8 and the hypothesis (Theorem 2.3 with $L=N-1$), we obtain the following.

Corollary 2.9 Suppose that Theorem 2.3 holds with $L=N-1$, and $\mathfrak a$, $\gamma$ and $\delta _\ast$ are the same as in Lemma 2.8. Then, if $p> 2(N-1)$, for $0<\delta <\delta _*$ we have

\[ \left\| \mathcal{T} [\mathfrak a] f \right\|_p\lesssim 2^{-k/p}\delta^{1-{(N+1)}/p} \|f\|_p. \]

Proof. By (2.14) and dyadic decomposition (of $\tilde a$ in the Fourier side), we have

(2.18)\begin{equation} \left\| \tilde\chi \mathcal{T} [\mathfrak a] f \right\|_p \le C \delta^{1- 1/p} \sum_{0\le \ell \le C } \left\|\mathcal{R}[\gamma_{s_{{\circ}}}^{\delta},a_\ell] f_\ell \right\|_p, \end{equation}

for some constant $C$ where $\|f_\ell \|_p=\|f\|_p$, and $a_\ell$ are symbols of type $(2^j,N-1, \tilde B)$ with $C^{-1}2^k\delta ^N\le 2^j \le C2^k\delta ^N$. Once we have this, the proof is straightforward. By Lemma 2.7, $\gamma _{s_{\circ }}^\delta \in \mathfrak V^d(N-1, B')$ for some $B'>0$. Since $\|f_l\|_p =\|f\|_p$, applying Theorem 2.3 with $L=N-1$, we have

\[ \left\| \tilde\chi \mathcal{T} [\mathfrak a] f \right\|_p \le C \sum_{l}\delta^{1- 1/p} (2^k\delta^N)^{-1/p} \|f_l\|_p \lesssim 2^{- k/p}\delta^{1-{(N+1)}/p} \|f\|_p \]

for $p> 2(N-1)$. Recalling (2.7), we combine this and (2.12) to get the desired bound.

It remains to show (2.18). In fact, after applying Lemma 2.8 we only need to adjust the support of the consequent symbol $\tilde a$ via by moderate decomposition and scaling. We omit details. (See the proof of [23, Lemma 2.8].)

3. Decoupling inequalities for curves

In this section, we prove the decoupling inequality, which is to be used to decompose the operator $\mathcal {T}[\mathfrak a]f$. In our earlier work [23], the averaging operator was decoupled by making use of decomposition based on a class of symbols that are adjusted to short subcurves. The same approach also works to prove Proposition 2.4. However, instead of following the previous strategy, we directly obtain a decoupling inequality associated with the conic sets:

\[ \Lambda_k(\delta,s_l), \quad 1\le l\le L, \]

while $\{s_1,\ldots,s_L\}\subset I$ is a collection of $\delta$-separated points contained in $I$. More precisely, we have the following.

Theorem 3.1 Let $0<\delta \le 1$ and $S:=\{s_1,\dots,s_L\}\subset I$ be a collection of $\delta$-separated points. Then, if $2\le p\le N(N+1)$, for any $\epsilon >0$ there is a constant $C_\epsilon =C_\epsilon (B)$, independent of $S$, such that

(3.1)\begin{equation} \big\| \sum_{1 \le l\le L} f_l \big\|_{L^p(\mathbb{R}^{d+1})}\le C_\epsilon \delta^{-\epsilon} \bigl(\sum_{1 \le l\le L} \|f_l\|_{L^p(\mathbb{R}^{d+1})}^2 \bigr)^{1/2} \end{equation}

holds whenever $\operatorname {supp} \widehat {f}_{l}\subset \Lambda _k(\delta,s_l)$.

Hölder's inequality gives $\big\| \sum _{1 \le l\le L} f_l \big\|_{p}\le C_\epsilon \delta ^{-\epsilon } \delta ^{1/p-1/2} (\sum _{1 \le l\le L} \|f_l\|_{p}^p)^{1/p}$. Interpolation with the trivial $L^\infty -\ell ^\infty L^\infty$ estimate yields the inequality:

(3.2)\begin{equation} \big\| \sum_{1 \le l\le L} f_l \big\|_{L^p(\mathbb{R}^{d+1})}\le C_{\epsilon}\delta^{{-}1+({N+1})/ {p}+\epsilon} \bigl(\sum_{1 \le l\le L}\left\| f_l \right\|_{L^p(\mathbb{R}^{d+1})}^p \bigr)^{ 1/p} \end{equation}

for $p>2N$ whenever $\operatorname {supp} \widehat {f}_{l}\subset \Lambda _k(\delta,s_l)$.

3.1 Decoupling inequalities for curves

Fixing $N\ge 2$, we now consider the slabs given by an anisotropic neighbourhood of the moment curve

\[ \gamma_{{\circ}}(s):=\left(s,\ {s^2}/{2!},\ldots, {s^{N+1}}/{(N+1)!}\right). \]

Definition 3.2 Let $0<\delta \le 1$ and $B\ge 1$. For $s \in I$, let $\mathbf {S}(s,\delta, B)$ denote the set of $(\tau,\xi ) \in \mathbb {R} \times \mathbb {R}^N$ such that

\[ B^{{-}1} \le | \langle \gamma_{{\circ} \phantom{1}}^{(N+1)}(s), (\tau,\xi) \rangle| \le B; \quad | \langle \gamma_{{\circ} \phantom{1}}^{(j)}(s),(\tau,\xi) \rangle| \le \delta^{N+1-j}, \quad j=1,\dots,N. \]

We now recall the decoupling inequality for such slabs as above which was shown in [1, 6] (see also [23, Corollary 2.15]).

Theorem 3.3 Let $0<\delta \le 1$ and $\{s_1, \ldots, s_L\}\subset I$ be a collection of $\delta$-separated points contained in $I$. Denote $\mathbf {S}_l=\mathbf {S}(s_l,\delta, B)$. Then, if $2 \le p\le N(N+1)$, for any $\epsilon >0$ there is a constant $C_\epsilon =C_\epsilon (B)$ such that

\[ \big\| \sum_{1 \le l\le L} F_l \big\|_{L^p(\mathbb{R}^{N+1})}\le C_\epsilon \delta^{-\epsilon} \bigl(\sum_{1 \le l\le L} \|F_l\|_{L^p(\mathbb{R}^{N+1})}^2 \bigr)^{1/2} \]

holds whenever $\operatorname {supp} \widehat {F}_{l}\subset \mathbf {S}_l$.

To show Theorem 3.1, we apply the decoupling inequality after projecting the sets $\Lambda _0(\delta,s_l)$ to the subspace $\mathrm V_\mu$ which is spanned by $\{G^{(0)}(\mu ) ,\dots, G^{(N)}(\mu )\}$. To do so, for $\mu \in I$ we consider a coordinate system $\mathbf {y}_\mu =\mathbf {y}_\mu (\tau,\xi )$ given by

(3.3)\begin{equation} \mathbf{y}_\mu=(y_\mu^0,\cdots, y_\mu^N)=(\langle G^{(0)}(\mu ),(\tau,\xi)\rangle, \ldots, \langle G^{(N)}(\mu ),(\tau,\xi)\rangle). \end{equation}

Recall that $\gamma \in \mathfrak V^d(N,B)$, so ${\rm Vol}(\langle G^{(0)}(\mu ), \ldots, G^{(N)}(\mu ))\ge 1/B$. Let $\delta, \delta '$ be positive numbers satisfying

(3.4)\begin{equation} 0< \delta<\delta' \le \delta^{N/(N+1)} \le1. \end{equation}

Then, it is easy to see that

(3.5)\begin{equation} (\delta')^{\ell+1} \le \delta^{\ell}, \quad \ell=1,\dots,N. \end{equation}

The following lemma shows that the projections of the sets $\Lambda _0(\delta,s_l)$ form a reverse $\delta /\delta '$-adapted cover after a proper linear change of variables (cf. [23, Lemma 3.3]) if $s_l$ are contained in an interval of length $\delta '$. Let $\mathrm D_\delta$ denote the $(N+1)\times (N+1)$ diagonal matrix given by

\[ \mathrm D_\delta=(\delta^{{-}N}e_1,\delta^{{-}N+1}e_2,\dots, \delta^{0}e_{N+1}). \]

Lemma 3.4 Let $\delta, \delta '$ be positive numbers satisfying (3.4) and $s' \in [\mu -\delta ',\mu +\delta ']$. Suppose $(\tau,\xi ) \in \Lambda _0(\delta,s')$. Then, we have

(3.6)\begin{gather} (4B)^{{-}1} \le |\langle \mathrm D_{\delta'} \mathbf{y}_\mu,\gamma_{\vphantom{1}\circ}^{(N+1)} \rangle | \le 4B, \end{gather}

(3.7)\begin{gather} \left|\left\langle \mathrm D_{\delta'} \mathbf{y}_\mu,\gamma_{\vphantom{1}\circ}^{(j)}\left( \frac{s'-\mu}{\delta'}\right) \right\rangle\right| \lesssim B\left({\delta}/{\delta'}\right)^{N+1-j}, \quad 1 \le j \le N. \end{gather}

Proof. Note that (3.6) is clear from (2.6). To prove (3.7), we first note that $\langle \mathbf {y}_\mu,\gamma _{\vphantom {1}\circ }^{(j)}(s) \rangle =(\delta ')^{N+1-j} \langle \mathrm D_{\delta '} \mathbf {y}_\mu, \gamma _{\vphantom {1}\circ }^{(j)}(s/\delta ') \rangle$. Thus, it is sufficient to show that

(3.8)\begin{equation} |\langle \mathbf{y}_\mu, \gamma_{\vphantom{1}\circ}^{(j)}(s'-\mu) \rangle| \lesssim B{\delta}^{N+1-j} \end{equation}

for $1 \le j \le N$. Recalling (3.3), we observe

\[ \langle \mathbf{y}_\mu, \gamma_{\vphantom{1}\circ}^{(j)}(s'-\mu) \rangle = \left\langle\sum_{\ell=j-1}^N G^{(\ell)}(\mu)\frac{(s'-\mu)^{\ell-j+1}}{(\ell-j+1)!},(\tau,\xi)\right\rangle. \]

Taylor's theorem gives

\[ \left |G^{(j-1)}(s')-\sum_{\ell=j-1}^N G^{(\ell)}(\mu)\frac{(s'-\mu)^{\ell-j+1}}{(\ell-j+1)!}\right|\le B |s'-\mu|^{N-j+2} \]

for $j=1,\dots,N$. Since $|s'-\mu |\le \delta '$ and $(\tau,\xi ) \in \Lambda _0(\delta,s')$, (3.8) follows by (3.5).

By Lemma 3.4 and Theorem 3.3, we can show that (3.1) holds if a $\delta$-separated set $\{s_1, \dots, s_L\}$ is contained in an interval of length $\lesssim \delta ^{N/(N+1)}$. More precisely, we have the following.

Lemma 3.5 Let $0<\delta \le 1$ and $\delta \le \delta '\le \delta ^{N/(N+1)}$. Let $\{s_1 ,\ldots,s_L \}\subset [\mu -\delta ' ,\mu +\delta ' ]$ be a collection of $\delta$-separated points. Then, if $2\le p\le N(N+1)$, for any $\epsilon >0$ there is a constant $C_\epsilon =C_\epsilon (B)$ such that (3.1) holds whenever $\operatorname {supp} \widehat {f}_{l}\subset \Lambda _k(\delta,s_l )$.

Proof. Set $\mathrm V_\mu =\operatorname {span} \{ \gamma '(\mu ),\dots, \gamma ^{(N)}(\mu )\}$ and let $\{v_{N+1},\ldots,v_d\}$ be an orthonormal basis of $\mathrm V_\mu ^\perp$ . Recalling that (2.3) holds with $L=N$, we write $\xi =\overline \xi +\sum _{j=N+1}^d y_j(\xi )v_j$ for $\overline \xi \in \mathrm V_\mu$. Changing variables

\[ (\tau,\xi) \rightarrow \mathrm Y_\mu(\tau,\xi):= (\mathbf{y}_\mu(\tau,\xi), y_{N+1}(\xi),\ldots,y_d(\xi)) \]

(see (3.3)), we may work with the coordinate system given by $\{ \mathbf {y}_\mu,y_{N+1},\ldots,y_d\}$ instead of $(\tau,\xi )$. We consider the linear map

\[ \mathrm Y_\mu^{\delta'} (\tau,\xi)=(\mathrm D_{\delta'} \mathbf{y}_\mu(\tau,\xi), y_{N+1}(\xi),\ldots,y_d(\xi)). \]

Since $\{s_1 ,\dots,s_L \}\subset [\mu -\delta ',\mu +\delta ']$ and $\delta '\le \delta ^{N/(N+1)}$, by Lemma 3.4 it follows that

(3.9)\begin{equation} \mathrm Y_\mu^{\delta'} ( \Lambda_0(\delta,s_l ) ) \subset \mathbf{S}_l \times \mathbb{R}^{d-N}:=\mathbf{S}\left(\frac{s_l -\mu}{\delta'}, C\frac{\delta}{\delta'}, 4B\right) \times \mathbb{R}^{d-N} \end{equation}

for some $C>0$ depending only on $B$. Applying Theorem 3.3 with $\delta$ replaced by $C\delta /\delta '$ and slabs $\mathbf {S}_l, 1\le l\le L$, and then using a trivial extension via Minkowski's inequality, we have

\[ \big\| \sum_{1\le l\le L}f_l \big\|_p\le C_{\epsilon} \delta^{-\epsilon} \bigl(\sum_{1\le l\le L}\left\| f_l \right\|_p^2 \bigr)^{1/2} \]

for $2\le p \le N(N+1)$ whenever $\operatorname {supp} \widehat f_l\subset \mathbf {S}_l \times \mathbb {R}^{d-N}$. Since the decoupling inequality is invariant under affine changes of variables, by undoing the change of variables $(\tau,\xi ) \rightarrow \mathrm Y_\mu (\tau,\xi )$ and rescaling $(\tau,\xi ) \rightarrow 2^{-k}(\tau,\xi )$, we obtain (3.1) whenever $\operatorname {supp} \widehat {f}_{l}\subset \Lambda _k(\delta,s_l )$.

3.2 Proof of Theorem 3.1

We now prove Theorem 3.1. Let $2 \le p\le N(N+1)$. For the purpose, for some $\alpha >0$ we assume that

\begin{equation}\big\| \sum_{1 \le l\le L} f_l \big\|_{L^p(\mathbb{R}^{d+1})}\le C \delta^{-\alpha} \bigl(\sum_{1 \le l\le L} \|f_l\|_{L^p(\mathbb{R}^{d+1})}^2\bigr)^{1/2} \quad \quad \quad {\mathfrak{D}(\alpha)}\end{equation}

holds for $0<\delta \le \delta _0:= (2^2B)^{-N-1}$ with a constant $C$, independent of $S$, whenever $\operatorname {supp} \widehat {f}_{l}\subset \Lambda _k(\delta,s_l)$, $1 \le l\le L$. Of course, ($\mathfrak{D}(\alpha)$) holds true if $\alpha \ge 1/2$ by Minkowski's and Hölder's inequalities. We set

\[ \delta'=\delta^{N/(N+1)}. \]

Let us denote $I _\nu$, $1\le \nu \le M$, be disjoint intervals of length $\rho \in (2^{-3}\delta ', 2^{-2}\delta ']$ which partition $I$. Let $s _\nu '$ be a point contained in $I _\nu$ such that $s_1', \dots, s_M'$ are separated at least by $2^{-4}\delta '$. We now claim that

(3.10)\begin{equation} \Lambda_k(\delta,s_l )\subset \Lambda_k(\delta',s' _\nu) \end{equation}

if $s_l\in I _\nu$. Indeed, by scaling it is sufficient to show $\Lambda _0(\delta,s_l )\subset \Lambda _0(\delta ',s' _\nu ).$ Let $(\tau,\xi )\in \Lambda _0(\delta,s_l )$. Then, it follows that $|\langle G^{(\ell )}(s_l),(\tau,\xi )\rangle |\le 2^5B \delta ^{1/(N+1)}(\delta ')^{N-\ell }$. By Taylor's theorem we have

\[ \langle G^{(j)}(s' _\nu),(\tau,\xi)\rangle=\sum_{\ell=j}^{N-1}\langle G^{(\ell)}(s_l),(\tau,\xi)\rangle\frac{(s'_\nu-s_l)^{\ell-j}}{(\ell-j)!}+\mathcal{E}, \]

where $|\mathcal {E}|\le 2B|s'_\nu -s_l|^{N-j}$. Therefore, we see that $(\tau,\xi )\in \Lambda _0(\delta ',s'_\nu )$.

Let $\operatorname {supp} \widehat {f}_{l}\subset \Lambda _k(\delta,s_l)$, $1 \le l\le L$. We write $\sum _{1\le l\le L}f_l=\sum _{1\le \nu \le M}\sum _{s_l\in I_\nu } f_l$. By (3.10), the Fourier support of $\sum _{s_l\in I_\nu } f_l$ is included in $\Lambda _k(\delta ',s' _\nu )$. Since $s'_\nu$ are separated by $2^{-4}\delta '$, ($\mathfrak{D}(\alpha)$) implies

\[ \big\| \sum_{1 \le l\le L} f_l \big\|_{L^p(\mathbb{R}^{d+1})}\le C \delta^{-{N\alpha}/{(N+1)}} \bigl(\sum_{1 \le \nu \le M} \|\sum_{s_l\in I_\nu} f_l\|_{L^p(\mathbb{R}^{d+1})}^2 \bigr)^{1/2} \]

for a constant $C$. Since the length of interval $I_\nu$ is less than $\delta ^{N/(N+1)},$ by Lemma 3.5 we have $\|\sum _{s_l\in I_\nu } f_l\|_{p}\le C_\epsilon \delta ^{-\epsilon } (\sum _{s_l\in I_\nu }\| f_l\|_{p}^2 )^{1/2}$. Therefore, combining this and the above inequality, we obtain

\[ \big\| \sum_{1 \le l\le L} f_l \big\|_{L^p(\mathbb{R}^{d+1})}\le C_\epsilon \delta^{-{N\alpha}/{(N+1)}-\epsilon} \bigl(\sum_{1 \le l\le L} \|f_l\|_{L^p(\mathbb{R}^{d+1})}^2\bigr)^{1/2} \]

for a constant $C_\epsilon$. This establishes the implication $\mathfrak D(\alpha )\to \mathfrak D(\epsilon + {N\alpha }/(N+1))$. Iteration of this implication suppresses $\alpha$ arbitrarily small.

4. Proof of Proposition 2.4

In this section, we prove Proposition 2.4 by making use of the decoupling inequality (3.2). As mentioned in § 2.1 (below Proposition 2.4), in order to prove Proposition 2.4, it suffices to show Theorem 2.3 with $L=N$. We first reduce the matter to obtaining estimates for $\mathcal {T}[\mathfrak a_0]$ with a suitable $\mathfrak a_0$.

4.1 Reduction

We begin by recalling $\gamma \in \mathfrak V^d(N,B)$ and $a$ is of type $(2^k,N,B)$. Let $\delta _*$ be the small number given in Lemma 2.8 and set

(4.1)\begin{equation} \delta_{{\circ}}=\min\{ \delta_*, (2^2B)^{{-}N}\}. \end{equation}

Let $\beta _0\in \mathrm C_0^\infty ([-1,1])$ such that $\beta _0= 1$ on $[-1/2,1/2]$. We set

\[ a_N(s,t,\xi)=a(s,t,\xi)\prod_{1\le j\le N-1} \beta_0 \left(100\,dB2^{{-}k}\delta_{{\circ}}^{{-}N} \langle \gamma^{(j)}(s),\xi\rangle \right). \]

Clearly, (2.4) holds on $\operatorname {supp} (a-a_N)$ with $L=N-1$ and $B$ replaced by $100\,dB\delta _{\circ }^{-N}$. Since $a$ is of type $(2^k,N,B)$, it is easy to see $(a-a_N)$ is a symbol of type $(2^k,N-1,B')$ for some $B'$. Thus, the hypothesis (Theorem 2.3 with $L=N-1$ and $B=B'$) gives the estimate

\[ \|\mathcal{R}[a-a_N]f\|_p\lesssim 2^{-(k/p)}\|f\|_p \]

for $p> 2(N-1)$. So, we need only to consider $\mathcal {R}[a_N]$ instead of $\mathcal {R}[a]$. Furthermore, by a moderate decomposition of $a_N$, we assume

\[ \operatorname{supp}_s a_N \subset [s_{{\circ}}-\delta_{{\circ}}, s_{{\circ}}+\delta_{{\circ}}] \]

for some $s_{\circ } \in (-1,1)$. We may assume that $s_{\circ }=\delta _{\circ }\nu$ for $\nu \in \mathbb {Z}$.

It is not difficult to see that the contribution of the frequency part $\{(\tau,\xi ): |\tau +\gamma (s)\cdot \xi | \gtrsim 2^{k+1} \delta _{\circ }^N, \, \forall s \in I\}$ is not significant. To see this, let us set

\[ {\mathfrak a}_0(s,t,\tau,\xi)= a_N(s,t,\xi) \beta_0 \left( \delta_{{\circ}}^{{-}2N} 2^{{-}2k}|\tau+\gamma(s)\cdot \xi |^2\right) \]

and $\mathfrak a_1=\mathfrak a_0-a_N$. Recalling (2.10), by Fourier inversion we have

\[ \mathcal{R}[a_N]f = \mathcal{T}[\mathfrak a_0]f+ \mathcal{T}[\mathfrak a_1]f. \]

The operator $\mathcal {T}[\mathfrak a_1]$ is easy to handle. Let us set $\mathfrak a=-i2^{k}\delta _{\circ }^{N}(\tau +\langle \gamma (s), \xi \rangle )^{-1} \partial _{t}\mathfrak a_1$. Then, by integration by parts in $t'$ and (2.10) we see $\mathcal {T} [\mathfrak a_1]=(2^{k}\delta _{\circ }^{N})^{-1}\mathcal {T} [\mathfrak a]$. Note that $|\tau +\gamma (s)\cdot \xi | \gtrsim 2^{k} \delta _{\circ }^N$ on $\operatorname {supp} \mathfrak a_1$ and so on $\operatorname {supp} \mathfrak a$. It is clear that $\mathfrak a$ satisfies (2.8) and (2.9) with $\delta =\delta _{\circ }$ and $B=C_1\delta _{\circ }^{-C}$ for some large $C,C_1$. Thus, Lemma 2.6 gives $\|\mathcal {T} [ \mathfrak a_1]f\|_p\lesssim 2^{-k}\|f\|_p$ for $p\ge 2.$

Therefore, the proof of Theorem 2.3 with $L=N$ is now reduced to show that

(4.2)\begin{equation} \left\| \mathcal{T}[\mathfrak a_0]f \right\|_{p} \le C 2^{-({k}/ p)}\|f\|_{p}, \quad p>2N. \end{equation}

4.2 Decomposition

For $n\ge 0$, let us set $\delta _n=2^n2^{-k/N}$ and

(4.3)\begin{equation} \mathfrak J_n= \delta_n\mathbb{Z}\cap I. \end{equation}

We consider

\[ \mathfrak G_N(s,\tau,\xi)=\sum_{0\le j\le N-1}(2^{{-}k}|\langle G^{(j)}(s),(\tau,\xi)\rangle|)^{{2N!}/{(N-j)}}, \]

by which we can decompose $\mathfrak a_0$ into the symbols contained in $\mathfrak A_k(\delta _n,s)$ for $s\in \mathfrak J_n$.

Set $\beta _\ast =\beta _0-\beta _0(2^{2N!}\cdot )$. Note that $\beta _0+\sum _{n\ge 1} \beta _\ast (2^{-2N! n} \cdot )=1$. Let $\zeta \in \mathrm C_0^{\infty }([-1,1])$ such that $\sum _{\nu \in \mathbb {Z}} \zeta (\cdot -\nu )=1$. We set

\[ \mathfrak a^{n}_\nu =\mathfrak a_0 \times \begin{cases} \beta_0 ( \delta_0^{{-}2N!} \, \mathfrak G_N ) \, \zeta(\delta_0^{{-}1}s-\nu), & \nu \in \mathfrak J_0, \ n=0, \\ \beta_\ast ( \delta_n^{{-}2N!} \, \mathfrak G_N) \, \zeta(\delta_n^{{-}1}s-\nu), & \nu \in \mathfrak J_n,\ n\ge 1. \end{cases} \]

Then, it follows that

(4.4)\begin{equation} \mathfrak a_0(s,t,\tau,\xi)= \sum_{n\ge 0}\sum_{\nu \in \mathfrak J_n} \mathfrak a_\nu^{n}(s,t,\tau,\xi). \end{equation}

Since $\delta _{\circ }$ is the fixed constant, it is clear that $C^{-1} \mathfrak a_0 \in \mathfrak A_k(\delta _{\circ },s_{\circ })$ for a large constant $C>0$. So, $\operatorname {supp} \mathfrak a_0 \subset \Lambda _k(\delta _{\circ },s_{\circ })$ and $\mathfrak G_N\lesssim 1$ for $(\tau,\xi )\in \operatorname {supp} \mathfrak a_\nu ^n$. Obviously, we may assume $\delta _n\lesssim 1$ since $\mathfrak a_\nu ^n=0$ otherwise.

The following tells that $\mathfrak a_{\nu }^{n}$ is contained in a proper symbol class.

Lemma 4.1 (cf. [23, Lemma 3.2])

For $n\ge 0$, there exists a constant $C$ such that $C^{-1}\mathfrak a_{\nu }^{n}\in \mathfrak A_k(\delta _n,\delta _n\nu )$.

Proof. Condition (2.8) trivially holds for $\mathfrak a=\mathfrak a_\nu ^n$. So, we only need to show (2.9) for $\delta =\delta _n$ and $s=\delta _n\nu$.

It is not difficult to see that $\mathfrak a_0$ satisfies (2.9) (see [23, (3.35)]). So it suffices to show (2.9) for $\beta _N(\delta _n^{-2N!}\mathfrak G_N(s,\tau,\xi ))$. By Leibniz's rule, it is enough to prove that

(4.5)\begin{equation} \big|\nabla_{\tau,\xi}\delta_n^{-(N-j)} 2^{{-}k} \big\langle G^{(j)}(s), {\mathcal{L}}_{\delta_n\nu}^{\delta_n}(\tau, \xi) \big\rangle \big|\lesssim\! 2^{{-}k}, \end{equation}

for $j=0,\ldots,d-1$. Note that if $|\delta _n\nu -s|\le \delta _n$, then

(4.6)\begin{equation} |({\mathcal{L}}_{s}^{\delta_n})^{{-}1}{\mathcal{L}}_{\delta_n \nu}^{\delta_n}(\tau,\xi)|\sim |(\tau,\xi)| \end{equation}

(see [23, Lemma 2.6]). Note that $\nabla _{\tau,\xi }\langle G^{(j)}(s), {\mathcal {L}}_{\delta _n\nu }^{\delta _n}(\tau, \xi )\rangle = ({\mathcal {L}}_{\delta _n\nu }^{\delta _n})^\intercal G^{(j)}(s)$. Thus, by (4.6) we get (4.5).

4.3 Proof of Proposition 2.4

By the reduction in § 4.1, it suffices to prove (4.2). Recalling (4.4) and applying the Minkowski inequality, we have

\[ \| \mathcal{T}[\mathfrak a_0] f\|_p\le \sum_{2^{{-}k/N} \le \delta_n\lesssim 1} \big\| \sum_{\nu \in \mathfrak J_n} \mathcal{T}[\mathfrak a_{\nu}^{n}]f \big\|_p. \]

Using Lemma 4.1, one can easily see that $\operatorname {supp} \mathfrak a_{\nu }^{n}\subset \Lambda _k(\delta _n, \delta _n\nu )$. Thus, we may use the decoupling inequality (3.2). Combining this and the above inequalities gives

\[ \| \mathcal{T}[\mathfrak a_0] f\|_p \le C_{\epsilon} \sum_{2^{{-}k/N} \le \delta_n\lesssim 1} {\delta_n}^{{-}1+({N+1})/ {p}+\epsilon} \bigl( \sum_{\nu \in \mathfrak J_n} \big\| \mathcal{T}[\mathfrak a_{\nu}^{n}]f \|_p^p \bigr)^{1/p} \]

for $2N< p<\infty$. Hence, for estimate (4.2) it suffice to show that

(4.7)\begin{equation} \|\mathcal{T} [\mathfrak a_{\nu}^{n}]f \|_p\lesssim \delta_n^{1-{(N+1)}/p}2^{-k/p}\|f \|_p, \quad p>2N. \end{equation}

Indeed, let $f_\nu (x,s)=\tilde \zeta (\delta _n^{-1}s-\nu ) f(x,s)$ where $\tilde \zeta \in \mathrm C_0^\infty ([-2,2])$ such that $\tilde \zeta =1$ on $\operatorname {supp} \zeta$. From (2.10) we see $\mathcal {T} [\mathfrak a_{\nu }^{n}]f=\mathcal {T} [\mathfrak a_{\nu }^{n}]f_\nu$. Combining this and (4.7), we have

\begin{align*} \bigl( \sum_{\nu \in \mathfrak J_n} \big\| \mathcal{T}[\mathfrak a_{\nu}^{n}]f \|_p^p \bigr)^{1/p}& \lesssim\delta_n^{1-{(N+1)}/p}2^{-k/p}\bigl( \sum_{\nu \in \mathfrak J_n} \big\|f_\nu \|_p^p \bigr)^{1/p}\\& \lesssim\delta_n^{1-{(N+1)}/p}2^{-k/p}\|f \|_p. \end{align*}

Therefore, taking the sum over $n$, we get (4.2), which proves Proposition 2.4.

It remains to prove (4.7). By Lemma 4.1, we have $C^{-1}\mathfrak a_{\nu }^{n} \in \mathfrak A_k(\delta _n,\delta _n\nu )$ for a constant $C>0$. For $n=0$, it is easy to show (4.7). Since $\delta _0=2^{-k/N}$, applying Lemma 2.6, we get

\[ \| \mathcal{T}[\mathfrak a_{\nu}^0]f\|_p\lesssim \delta_0^{1- 1/p}\|f\|_p = \delta_0^{1-{(N+1)}/p}2^{-k/p}\|f\|_p, \quad 2\le p\le \infty. \]

For $n\ge 1$, we need to decompose $\mathfrak a_{\nu }^{n}$ further. Let us set

\[ \mathfrak a_{\nu,1}^{n} (s,t,\tau,\xi) = \mathfrak a_{\nu}^{n} (s,t,\tau,\xi) (1- \beta_0 )\left( 10 \delta_n^{{-}2N!} |\langle 2^{{-}k}G(s),(\tau,\xi)\rangle |^{2(N-1)!}\right) \]

and $\mathfrak a_{\nu,0}^{n} = \mathfrak a_{\nu }^{n}-\mathfrak a_{\nu,1}^{n}$, so we have $\mathfrak a_{\nu }^{n} = \mathfrak a_{\nu,1}^{n}+\mathfrak a_{\nu,0}^{n}.$ We note that $C^{-1} \mathfrak a_{\nu,i}^{n} \in \mathfrak A_k(\delta _n,\delta _n\nu )$, $i=0,1$ for some $C>0$. This can be shown by following the proof of Lemma 4.1. So, we omit the detail.

We now decompose $\mathcal {T} [\mathfrak a_{\nu }^{n}]f=\mathcal {T} [\mathfrak a_{\nu,1}^{n}]f+\mathcal {T} [\mathfrak a_{\nu,0}^{n}]f.$ For (4.7), it suffices to show

(4.8)\begin{equation} \|\mathcal{T} [\mathfrak a_{\nu,i}^{n}]f \|_p \le C \delta_n^{1-{(N+1)}/p} 2^{-k/p}\|f \|_p, \quad i=0,1, \end{equation}

for $p>2N-2$. It is clear that (2.13) holds with $\delta =\delta _n$, $s_{\circ }=\delta _n\nu$, and some large $B$ on $\operatorname {supp} \mathfrak a_{\nu,1}^{n}$. By Corollary 2.9, we have (4.8) for $i=1$ if $p>2N-2$. The operator $\mathcal {T} [\mathfrak a_{\nu,0}^{n}]$ can be handled in the same manner as $\mathcal {T}[\mathfrak a_1]$ since

(4.9)\begin{equation} |\tau+\langle\gamma(s),\xi\rangle|\gtrsim \delta_n^{N} 2^{k} \end{equation}

holds on $\operatorname {supp} \mathfrak a_{\nu,0}^{n}$. We set $\mathfrak a=-i2^{k}\delta _n^{N}(\tau +\langle \gamma (s), \xi \rangle )^{-1} \partial _{t}\mathfrak a_{\nu,0}^{n}$. Integration by parts in $t'$ and (2.10) yields $\mathcal {T} [\mathfrak a_{\nu,0}^{n}]=(2^{k}\delta _n^{N})^{-1}\mathcal {T} [\mathfrak a]$. Using (4.9) and the fact that $C^{-1} \mathfrak a_{\nu,0}^{n} \in \mathfrak A_k(\delta _n,\delta _n\nu )$ for some $C>0$, one can easily verify that (2.8) and (2.9) hold for $\mathfrak a$ with $\delta =\delta _n$, $s_{\circ }=\delta _n\nu$. Thus, by Lemma 2.6, we have

\[ \|\mathcal{T} [\mathfrak a_{\nu,0}^{n}]f \|_p \lesssim \delta_n^{1-1/p} (\delta_n^N2^{k})^{{-}1}\|f\|_p \lesssim \delta_n^{1-{(N+1)}/p} 2^{-k/p}\|f \|_p \]

for $p\ge 2$, which gives (4.8) for $i=0$. For the second inequality we use the fact that $\delta _n\ge 2^{-k/N}$.

5. Proof of Theorem 1.2

We first prove the sufficiency part, that is to say, estimate (1.2) with $\alpha =1-1/p$ for $1\le p< p_d$ by making use of Theorem 2.3.

5.1 Proof of estimate (1.2) with $\alpha =1-1/p$

We make use of the argument in [28, 31]. As mentioned before, it suffices to prove (2.1) by duality. Let $P_k$ denote the (Littlewood–Paley projection) operator defined by

\[ \mathcal{F}(P_kg)(\xi,\tau)=\beta(2^{{-}k}|(\xi,\tau)|)\widehat g(\xi,\tau), \quad k\ge1 \]

for $\beta \in \mathrm C_0^\infty ([1/2,2])$. Recall that $\beta _0\in \mathrm C_0^\infty ([-1,1])$ such that $\beta _0= 1$ on $[-1/2,1/2]$ and set $\beta _\ast (t)=\beta _0(C_0^{-1}2^{-6}t)-\beta _0(C_0 2^{6}t)$. Here, $C_0=1+2\sup \{|\gamma (s)|+|\gamma '(s)|: s \in \operatorname {supp} \psi \}$. Let $f_k$ be given by

\[ \widehat{f_k}(\xi,u)=\beta_\ast(2^{{-}k} |(\xi,u)|) \widehat f(\xi,u). \]

We claim that

(5.1)\begin{equation} \big\| \bigl(\sum_{k \ge1}| P_k \mathcal{R} f|^2 \bigr)^{1/2} \big\|_p \lesssim \big\| \bigl( \sum_{k\ge1} 2^{-{2k}/p} | f_k|^2 \bigr)^{1/2} \big\|_p+\|f\|_{L_{- M}^p} \end{equation}

for $p>2d$ and $M\gg 1$. Then, (2.1) follows by the Littlewood–Paley inequality.

Let $\tilde \beta =\beta _0(2^{-3}\,\cdot )-\beta _0(C_02^{3}\,\cdot )$ Considering an operator $\mathcal {R}_k$ given by

\[ \mathcal{F}_x (\mathcal{R}_kf)(\xi,t)=\tilde\beta({|\xi|}/{2^k}) \mathcal{F}_x(\mathcal{R}f)(\xi,t), \]

we decompose

(5.2)\begin{equation} P_k \mathcal{R}f=P_k \mathcal{R}_k f_k+P_k \mathcal{R}_k (f-f_k)+P_k(\mathcal{R}-\mathcal{R}_k) f. \end{equation}

In what follows, we show that the contributions from the second and third terms are negligible. In fact, for any $M\ge 1$ if $p\ge 1$, we have

(5.3)\begin{equation} \big\| \bigl(\sum_k |P_k \mathcal{R}_k(f-f_k)|^2 \bigr)^{1/2}\big\|_p \lesssim \|f\|_{L_{{-}M}^p} \end{equation}

and (5.4).

To see (5.3), note $\mathcal {F}_x(\mathcal {R}_k g)(\xi,t')=\int m(\xi,t',u) \widehat g(\xi,u)\,{\rm d}u$ where

\[ m(\xi,t',u)=(2\pi)^{{-}1}\chi(t') \tilde\beta({|\xi|}/{2^k}) \int {\rm e}^{i(s u-t'\gamma(s)\cdot \xi)}\psi(s)\,{\rm d}s. \]

Set $g=f-f_k$. Since $|(\xi,u)|\ge C_0 2^{k+5}$ or $|(\xi,u)| \le C_0^{-1}2^{k-5}$ on $\operatorname {supp} \mathcal {F} (f-f_k)$, we have $|u| \ge C_0 |\xi |$ if $C_0^{-1}2^{k-4}\le |\xi | \le 2^{k+3}$. Therefore, integration by parts gives

\[ |\partial_{\xi,u}^\alpha m(\xi,t',u)| \lesssim 2^{{-}kN} (1+|(\xi,u)|)^{{-}N}, \quad (\xi,u)\in \operatorname{supp} \widehat g \]

for any $\alpha$ and $N\ge 1$. Note that $\textstyle P_k \mathcal {R}_kg(x,t)=\int K(x,y,t,s') g(y,s')\,{\rm d}y{\rm d}s'$ where

\[ K(x,y,t,s')=\frac1{(2\pi)^{d+1}}\int {\rm e}^{i(x-y,t-t')\cdot(\xi,\tau)}\,{\rm e}^{{-}is'u}\beta\left(\frac {|(\xi,\tau)|}{2^{k}}\right) m(\xi,t',u)\,{\rm d}\xi\,{\rm d}\tau\,{\rm d}u\,{\rm d}t'. \]

Therefore, $|\partial _{\xi,u}^\alpha m(\xi,t',u)| \lesssim 2^{-kN} 2^{-jN}$ for $(\xi,u) \in \operatorname {supp} \widehat g$ and integration by parts shows

\[ |K(x,y,t,s')| \lesssim 2^{{-}kN}2^{{-}jN}(1+|x-y|+|s'|)^{{-}N}(1+|t|)^{{-}N}. \]

Decomposing $\mathcal {R}_k(f-f_k)=\sum _{j}\mathcal {R}_kP_j(f-f_k)$, we get (5.3) for any $M\ge 1$ and $p\ge 1$.

We now show

(5.4)\begin{equation} \big\| \bigl( \sum_k | P_k(\mathcal{R}-\mathcal{R}_k)f |^2 \bigr)^{1/2} \big\|_p\lesssim \|f\|_{L_{{-}M}^p} \end{equation}

for $p\ge 1$ and $M\ge 1$. We write $\mathcal {F}(\mathcal {R}f-\mathcal {R}_kf)(\xi,\tau )=\int b(s,\xi,\tau )\mathcal {F}_xf(\xi,s)\,{\rm d}s$ where

\[ b(s,\xi,\tau)=\frac1{2\pi}\int\,{\rm e}^{it'(\gamma(s)\cdot \xi-\tau)} \left( 1-\tilde\beta({|\xi|}/{2^k})\right) \chi(t')\,{\rm d}t' \psi(s). \]

Since $|\xi | \le C_0^{-1}2^{k-2}$ or $|\xi |\ge 2^{k+2}$ on $\operatorname {supp} \mathcal {F}_x(\mathcal {R}f-\mathcal {R}_kf)$, we have $|\tau | \ge C_0 |\xi |$ if $2^{k-1} \le |(\xi,\tau )| \le 2^{k+1}$. Integration by parts gives $|\partial _\xi ^\alpha b(s,\xi,\tau )|\lesssim 2^{-kN}$ for any $\alpha$ and $N$. Hence,

(5.5)\begin{equation} \|P_k(\mathcal{R} -\mathcal{R}_k) f\|_{p} \lesssim 2^{{-}kN} \|f\|_p, \quad p\ge 1 \end{equation}

for all $N\ge 1$. Since $|\xi | \le C_0^{-1}2^{k-2}$ on $\operatorname {supp}\mathcal {F}(P_k(\mathcal {R}-\mathcal {R}_k)f)$, similarly as in the proof of (5.3), we have $\|P_k(\mathcal {R} -\mathcal {R}_k) P_jf\|_{p} \lesssim 2^{-jN} \|P_j f\|_p$ for $j\ge k+C'$ for some $C'\ge 1$. Estimate (5.5) gives $\|P_k(\mathcal {R} -\mathcal {R}_k) P_jf\|_{p} \lesssim 2^{-kN} \|P_j f\|_p$ for $j\le k+C'$. Combining those estimates, we get (5.4).

Therefore, estimate (5.1) follows if we show

(5.6)\begin{equation} \big\| \bigl(\sum_k|P_k \mathcal{R}_k f_k|^2 \bigr)^{1/2} \big\|_p \lesssim \big\| \bigl( \sum_{k\ge1} 2^{-{2k}/p} | f_k|^2 \bigr)^{1/2} \big\|_p \end{equation}

for $p>2d$. This can be done by using [28, Theorem 1] and (2.5) (also see [1, 29, 31]). Indeed, let $\tilde \beta \in \mathrm C_c^\infty ((1/4,4))$ such that $\tilde \beta \beta =\beta$. Consider the operator $\tilde P_k$ given by $\mathcal {F}(\tilde P_kg)(\xi,\tau )=\tilde \beta (2^{-k}|(\xi,\tau )|) \widehat g(\xi,\tau )$. Note that $P_k\mathcal {R}_k f_k=P_k \tilde P_k \mathcal {R}_k f_k$.

Let us denote the centre of a cube $Q$ by $(x_Q,t_Q)$ and set

\[ \mathcal{E}_Q=\{(y,s): \text{dist}( y-x_Q, t_Q \gamma(I)) \le 10 \text{diam} (Q), s \in I\}. \]

Since $T_k=\tilde P_k\mathcal {R}_k$ and $\mathcal {E}_Q$ satisfy the assumptions in [28, Theorem 1], by using (2.5) we obtain (5.6). We omit the details.

5.2 Sharpness of smoothing order

In this section, we show upper bounds on the smoothing order $\alpha$ for which $L^p-L_\alpha ^p$ estimate for $\mathfrak Rf$ holds when $\gamma$ is of maximal type $L$. In [31], those bounds were obtained for $d=2$. Modifying the examples in [31], we show the following.

Proposition 5.1 Let $d\ge 3$, $L\ge d$ and $1 \le p \le \infty$. Let $\psi$ and $\chi$ be nontrivial, nonnegative continuous functions supported in the interiors of $I$ and $[1,2]$, respectively. Suppose there is an $s_{\circ }$ such that $\psi (s_{\circ })\neq 0$ and $\gamma$ is of type $L$ at $s_{\circ }$. Then, $\mathfrak Rf$ maps $L^p$ boundedly to $L_\alpha ^p$ only if

\[ (i)\ \alpha\le 1-p^{{-}1}, \quad (ii)\ \alpha\le (2d)^{{-}1}, \quad (iii)\ \alpha\le (Lp)^{{-}1} . \]

In particular, the upper bound $(i)$ provides the necessity part of Theorem 1.2, thus, the proof Theorem 1.2 is completed. We prove the upper bounds $(i)$, $(ii)$ and $(iii)$, separately.

Proof. Proof of (i)

Let $t_{0} \in (1,2)$ such that $\chi (t_{0})>0$. We choose $\zeta \in \mathcal {S}(\mathbb {R}^{d})$ such that $\zeta \ge 1$ on $[-1,1]^{d}$, $\operatorname {supp} \widehat \zeta \subset [1/2,4]^d$, and $\widehat \zeta =1$ on $[1,2]^d$. Let $\psi _0\in \mathrm C_c^\infty ((-1,1))$ satisfy $\psi _0=1$ on $[-1/2,1/2]$. We take

\[ f(x,t)=\zeta(\lambda x)\psi_0(\lambda r_0 |t-t_{0}|), \]

where $r_0=1+\sup _{s \in I}|\gamma (s)|$. Note $\mathfrak Rf(x,s) \gtrsim \lambda ^{-1}$ if $|x+t_{0}\gamma (s)|\le c \lambda ^{-1}$ and $|s-s_{\circ }|< c$ for a small constant $c>0$. Thus, $\| \mathfrak Rf \|_{p} \gtrsim \lambda ^{-1-d/p}$. Since

\[ \mathcal{F}_x(\mathfrak Rf({\cdot}, s))(\xi) = \lambda^{{-}d} \psi(s)\int \widehat \zeta(\lambda^{{-}1}\xi)\,{\rm e}^{it\gamma(s)\cdot \xi}\psi_0(\lambda|t-t_{0}|)\chi(t)\,{\rm d}t, \]

it follows that $\operatorname {supp}_\xi \mathcal {F}_x(\mathfrak Rf)$ is included in $\{ \xi : |\xi | \sim \lambda \}$. Hence, $\| \mathfrak Rf(\cdot,s) \|_{L_\alpha ^p(\mathbb {R}^{d};{\rm d}x)} \gtrsim \lambda ^{\alpha -1-d/p}$, so we have $\| \mathfrak Rf\|_{L_\alpha ^p(\mathbb {R}^{d+1})} \gtrsim \lambda ^{\alpha -1-d/p}$. Since $\|f\|_p \lesssim \lambda ^{-(d+1)/p}$, we get $\alpha \le 1-1/p$.

Proof. Proof of (ii)

Let $\tilde I \subset (-1,1)$ be a nonempty compact interval such that (1.1) holds for $s \in \tilde I$. Also, we fix a constant $\rho \gg 1$ to be chosen later. Let $\{s_\ell \}\subset \tilde I$ be a collection of $\rho \lambda ^{-1/d}$-separated points which are as many as $C\rho ^{-1}\lambda ^{1/d}$. Since $G(s_\ell ), G'(s_\ell ), \ldots, G^{(d-1)}(s_\ell )$ are linearly independent in $\mathbb {R}^{d+1}$, there is a unit vector $\Xi _\ell \in ( \operatorname {span}\{ G^{(j)}(s_\ell ): j=0,1,\ldots,d-1\} )^\perp$.

Let $\phi \in \mathcal {S}(\mathbb {R}^{d+1})$ such that $\phi \ge 1$ on $[-3r_0,3r_0]^{d+1}$ and $\widehat \phi$ is supported in $[-1,1]^{d+1}$ where $r_0=1+\sup _{s \in I} |\gamma (s)|$. Let $\varepsilon _\ell \in \{\pm 1\}$ be independent random variables. We consider

\[ f(x,t)=\sum_\ell \varepsilon_\ell f_\ell(x,t):= \sum_\ell \varepsilon_\ell \phi(x,t) {\rm e}^{i\lambda \Xi_\ell \cdot (t,x)}. \]

Since $\langle \Xi _\ell, G^{(j)}(s_\ell ) \rangle =0$ for $j=0,\dots,d-1$, by Taylor's theorem we have

(5.7)\begin{equation} \langle \Xi_\ell, G(s) \rangle =\langle \Xi_\ell, G^{(d)}(s_\ell) \rangle(s-s_\ell)^{d}/d!+O(|s-s_\ell|^{d+1}). \end{equation}

Thus, $|t \langle \Xi _\ell, G(s)\rangle | \le 2^{-2}\lambda ^{-1}$ whenever $s \in I_\ell :=\{ s \in \tilde I : |s-s_\ell | \le c \lambda ^{-1/d}\}$ for a $c>0$ small enough. Noting that

(5.8)\begin{equation} \mathfrak Rf_\ell(x,s)= {\rm e}^{i\lambda \Xi_\ell \cdot (0,x)} \psi(s)\int \phi (x+t\gamma(s),t ) {\rm e}^{i\lambda t\Xi_\ell \cdot G(s)} \chi(t)\,{\rm d}t, \end{equation}

we see $|\mathfrak Rf_\ell (x,s)| \gtrsim 1$ if $(x,s) \in B_\ell :=[-c,c]^d\times I_\ell.$ Thus, $\sum _\ell \left \| \mathfrak Rf_\ell \right \|_{L^p(B_\ell )}^p \gtrsim \rho ^{-1}.$ Meanwhile, by (5.8), (5.7) and integration by parts in $t$ we have $|\mathfrak Rf_m(x,s)| \lesssim (1+\lambda |s_\ell -s_m|^{d})^{-N}$ for any $N\ge 1$ if $m\neq \ell$ and $s \in I_\ell$. Since $\{s_\ell \}$ are $\rho \lambda ^{-({1}/{d})}$-separated, it is easy to see

\[ \sum_\ell \big\| \sum_{m\neq \ell} |\mathfrak Rf_m| \big\|_{L^p(B_\ell)}^p \lesssim \sum_\ell \sum_{m \neq \ell} (1+\lambda |s_\ell-s_m|^{d})^{{-}pN} \lambda^{- 1/d} \lesssim \rho^{{-}pdN-1}. \]

Therefore, taking $\rho,N$ sufficiently large, we have $\|\mathfrak Rf \|_p^p \gtrsim \rho ^{-1}$ for any choice of $\varepsilon _\ell$.

By our choice of $\phi$ it follows that $\mathcal {F}_x (\mathfrak Rf)$ is supported on $\{\xi : C_1\lambda \le |\xi | \le C_2 \lambda \}$ for some positive constant $C_1, C_2$. Thus, $\| \mathfrak Rf \|_{L_\alpha ^p} \gtrsim \lambda ^\alpha \|\mathfrak Rf\|_p$. Combining this with the $L^p-L_\alpha ^p$ estimate gives $\lambda ^\alpha \le C \|f\|_p$ for any choice of $\varepsilon _\ell$. By Khintchine's inequality we have $\mathbb {E} (\| f \|_p^p) \sim \int (\sum _\ell | f_\ell |^2 )^{p/2}\,{\rm d}x\,{\rm d}t \sim C_\rho \lambda ^{{p}/{2d}}$. Therefore, we see $\lambda ^\alpha \lesssim \lambda ^{1/{2d}}$ and then $\alpha \le 1/(2d)$ taking $\lambda \to \infty$.

Proof. Proof of (iii)

Since $\gamma$ is of type $L$ at $s_{\circ }$, by an affine transformation and taking $\psi$ supported near $s_{\circ }$, we may assume

\[ \gamma(s+s_{{\circ}})=\gamma(s_{{\circ}})+(s^{a_1} \varphi_1(s),\dots, s^{a_d} \varphi_d(s)) \]

for $1\le a_1 <\cdots < a_d=L$ and smooth functions $\varphi _j$, $j=1,\ldots,d$, where $\|\varphi _j-1/a_j!\|_{\mathrm C^{a_d+1}(I)}\le c$ for a small constant $c>0$. We may also assume $s_{\circ }=0$ and furthermore $\gamma (0)=0$ by replacing $f(x,t)$ by $f(x-t\gamma (0),t)$.

Let $\phi _1\in \mathcal {S}(\mathbb {R})$ such that $\phi _1 \ge 1$ on $[-1,1]$, and $\operatorname {supp} \widehat \phi _1\subset [1/2,4]$ with $\widehat \phi _1=1$ on $[1,2]$. Let $\psi _0\in \mathrm C_c^\infty ((-1,1))$ with $\psi _0=1$ on $[-1/2,1/2]$. We consider

\[ f(x,t)=\prod_{j=1}^{d-1} \psi_0 ( \lambda^{a_j/L}x_j ) \phi_1 ( \lambda x_{d} ) \chi(t). \]

Denoting $\|a\|=\sum _{j=1}^d a_j$, we have $\|f\|_p \lesssim \lambda ^{-\|a\|/(Lp)}$. Set $E_\lambda =\{ (x,s) \in \mathbb {R}^d \times I: |x_j| \le c \lambda ^{-a_j/L}, j=1,\ldots,d, \quad |s| \le c \lambda ^{-1/L} \}$ for a sufficiently small $c>0$. Since $\gamma (s)=(s^{a_1} \varphi _1(s),\dots, s^{a_d} \varphi _d(s))$, $| \langle x+t\gamma (s),e_j \rangle | \le 2^{-1}\lambda ^{-a_j/L},$ $j=1,\dots,d$, for $(x,s) \in E_\lambda$ and $t\in [1,2]$. So, $\mathfrak Rf (x,s)\gtrsim 1$ for $(x,s) \in E_\lambda$. This gives $\| \mathfrak Rf\|_p\gtrsim \lambda ^{-(\|a\|+1)/(Lp)}$. Since $\operatorname {supp} \mathcal {F}_{x_{d}} (\mathfrak Rf) \subset \{ \xi _{d} : |\xi _{d}| \sim \lambda \}$, $\| \mathfrak Rf \|_{L_\alpha ^p} \gtrsim \lambda ^{\alpha -(\|a\|+1)/(Lp)}.$ Therefore, we obtain $\alpha \le 1/(Lp)$.