Article contents
Schützenberger groups of polynomials in the semigroup of entire functions
Published online by Cambridge University Press: 14 November 2011
Synopsis
Let 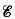 denote the semigroup, under composition, of all entire functions of a complex variable and for
denote the semigroup, under composition, of all entire functions of a complex variable and for 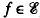 , let Γ(f) denote the Schützenberger group of the ℋ-class of
, let Γ(f) denote the Schützenberger group of the ℋ-class of 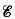 which contains f. The main results of this paper completely describe Γ(P) where P is a polynomial function. Γ(P) is trivial if P is a constant function. If Deg (P) (the degree of P) is one, then Γ(P) is isomorphic to the group of all matrices of the form
which contains f. The main results of this paper completely describe Γ(P) where P is a polynomial function. Γ(P) is trivial if P is a constant function. If Deg (P) (the degree of P) is one, then Γ(P) is isomorphic to the group of all matrices of the form 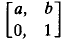 where a and b are complex numbers with a ≠ 0. If Deg (P) > 1, then Γ(P) is isomorphic to ℂM, the multiplicative group of nonzero complex numbers if and only if P(z) = α(z +β)n + γ where α ≠ 0. If P is not of this form and Deg (P) > 1, then Γ (P)is a finite cyclic group and its order can be determined by defining
where a and b are complex numbers with a ≠ 0. If Deg (P) > 1, then Γ(P) is isomorphic to ℂM, the multiplicative group of nonzero complex numbers if and only if P(z) = α(z +β)n + γ where α ≠ 0. If P is not of this form and Deg (P) > 1, then Γ (P)is a finite cyclic group and its order can be determined by defining 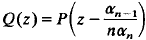 (where αn−1 and α n are the coefficients in P of zn−1 and zn respectively) and then inspecting the coefficients of Q.
(where αn−1 and α n are the coefficients in P of zn−1 and zn respectively) and then inspecting the coefficients of Q.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 105 , Issue 1 , 1987 , pp. 43 - 60
- Copyright
- Copyright © Royal Society of Edinburgh 1987
References
- 3
- Cited by


