Hostname: page-component-77c89778f8-5wvtr Total loading time: 0 Render date: 2024-07-21T11:10:56.158Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasilinear elliptic inequalities with Hardy potential and nonlocal terms

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  24 July 2020

Marius Ghergu ,
Paschalis Karageorgis  and
Gurpreet Singh
Marius Ghergu
Affiliation:
School of Mathematics and Statistics, University College Dublin, Belfield, Dublin 4, Ireland Institute of Mathematics Simion Stoilow of the Romanian Academy, 21 Calea Grivitei St., Bucharest, 010702, Romania ([email protected])
Paschalis Karageorgis
Affiliation:
School of Mathematics, Trinity College Dublin, Ireland ([email protected]; [email protected])
Gurpreet Singh
Affiliation:
School of Mathematics, Trinity College Dublin, Ireland ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the quasilinear elliptic inequality

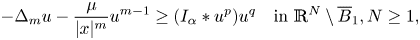\[ -\Delta_m u - \frac{\mu}{|x|^m}u^{m-1} \geq (I_\alpha*u^p)u^q \quad\mbox{in }\mathbb{R}^N\setminus \overline B_1, N\geq 1, \]
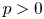where $p>0$, 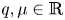$q, \mu \in \mathbb {R}$, 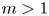$m>1$ and 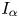$I_\alpha$ is the Riesz potential of order 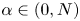$\alpha \in (0,N)$. We obtain necessary and sufficient conditions for the existence of positive solutions.

Keywords

Quasilinear elliptic inequalitiesm-Laplace operatorHardy term

MSC classification

Primary: 35J62: Quasilinear elliptic equations
Secondary: 35A23: Inequalities involving derivatives and differential and integral operators, inequalities for integrals 35B09: Positive solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 3 , June 2021 , pp. 1075 - 1093
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bidaut-Véron, M. F. and Pohozaev, S.. Nonexistence results and estimates for some nonlinear elliptic problems. J. Anal. Math. 84 (2001), 1–49.CrossRefGoogle Scholar
Caristi, G., D'Ambrosio, L. and Mitidieri, E.. Liouville theorems for some nonlinear inequalities. Proc. Steklov Inst. Math. 260 (2008), 90–111.CrossRefGoogle Scholar
Chen, H. and Zhou, F.. Classification of isolated singularities of positive solutions for Choquard equations. J. Differ. Equ. 261 (2016), 6668–6698.CrossRefGoogle Scholar
Chen, H. and Zhou, F.. Isolated singularities of positive solutions for Choquard equations in sublinear case. Commun. Contemp. Math. 20 (2018), art no 1750040.CrossRefGoogle Scholar
D'Ambrosio, L. and Mitidieri, E.. A priori estimates, positivity results, and nonexistence theorems for quasilinear degenerate elliptic inequalities. Adv. Math. 224 (2010), 9670–1020.CrossRefGoogle Scholar
Filippucci, R. and Ghergu, M.. Singular solutions for coercive quasilinear elliptic inequalities with nonlocal terms. Nonlinear Anal. 197 (2020), art no 111857.CrossRefGoogle Scholar
Ghergu, M. and Singh, G.. On a class of mixed Choquard–Schrödinger–Poisson systems. Discrete Contin. Dyn. Syst. B 12 (2019), 297–309.CrossRefGoogle Scholar
Ghergu, M. and Taliaferro, S.. Pointwise bounds and blow-up for Choquard–Pekar inequalities at an isolated singularity. J. Differ. Equ. 261 (2016), 189–217.CrossRefGoogle Scholar
Ghergu, M., Karageorgis, P. and Singh, G.. Positive solutions for quasilinear elliptic inequalities and systems with nonlocal terms. J. Differ. Equ. 268 (2020), 6033–6066.CrossRefGoogle Scholar
Lieb, E. and Loss, M.. Analysis. Graduate Studies in Mathematics, vol. 14, 2nd edn (Rhode-Island USA: Amer., Math. Soc., 2001).Google Scholar
Liskevich, V., Lyakhova, S. and Moroz, V.. Positive solutions to nonlinear $p$-Laplace equations with Hardy potential in exterior domains. J. Differ. Equ. 232 (2007), 212–252.CrossRefGoogle Scholar
Mitidieri, E. and Pohozaev, S. I.. A priori estimates and blow up of solutions to nonlinear partial differential equations. Proc. Steklov Inst. Math. 234 (2001), 1–367.Google Scholar
Moroz, V. and Van Schaftingen, J.. Nonexistence and optimal decay of supersolutions to Choquard equations in exterior domains. J. Differ. Equ. 254 (2013), 3089–3145.CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J.. A guide to the Choquard equation. J. Fixed: Point Theory Appl. 19 (2017), 773–813.Google Scholar
Singh, G.. Nonlocal perturbations of the fractional Choquard equation. Adv. Nonlinear Anal. 8 (2019), 694–706.CrossRefGoogle Scholar
Wang, Y. and Hajaiej, H.. Boundary singularity of Choquard equation in the half space. J. Math. Pures Appl. 126 (2019), 232–248.CrossRefGoogle Scholar