Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T20:25:41.773Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal global asymptotic behaviour of the solution to a class of singular Dirichlet problems

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  17 September 2020

Zhijun Zhang
Zhijun Zhang*
Affiliation:
School of Mathematics and Information Sciences, Yantai University, Yantai264005, Shandong, People's Republic of China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is mainly concerned with the global asymptotic behaviour of the unique solution to a class of singular Dirichlet problems − Δu = b(x)g(u), u > 0, x ∈ Ω, u|∂Ω = 0, where Ω is a bounded smooth domain in ℝn, g ∈ C1(0, ∞) is positive and decreasing in (0, ∞) with 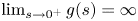$\lim _{s\rightarrow 0^+}g(s)=\infty$, b ∈ Cα(Ω) for some α ∈ (0, 1), which is positive in Ω, but may vanish or blow up on the boundary properly. Moreover, we reveal the asymptotic behaviour of such a solution when the parameters on b tend to the corresponding critical values.

Keywords

Semi-linear elliptic equationsa singular nonlinearityboundary value problemsthe unique solutionglobal asymptotic behaviour

MSC classification

Primary: 35J75: Singular elliptic equations
Secondary: 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 3 , June 2021 , pp. 1116 - 1134
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsaedi, R., Mâagli, H. and Zeddini, N.. Exact behavior of the unique positive solution to some singular elliptic problem in exterior domains. Nonlinear Anal. 119 (2015), 186–198.CrossRefGoogle Scholar
Ben Othman, S., Mâagli, H., Masmoudi, S. and Zribi, M.. Exact asymptotic behaviour near the boundary to the solution for singular nonlinear Dirichlet problems. Nonlinear Anal. 71 (2009), 4137–4150.CrossRefGoogle Scholar
Berhanu, S., Gladiali, F. and Porru, G.. Qualitative properties of solutions to elliptic singular problems. J. Inequal. Appl. 3 (1999), 313–330.Google Scholar
Bingham, N. H., Goldie, C. M., Teugels, J. L.. Regular variation, encyclopedia of mathematics and its applications 27. (Cambridge: Cambridge University Press, 1987).Google Scholar
Boccardo, L.. Dirichlet problems with singular and gradient quadratic lower order terms. ESAIM Control Optim. Calc. Var. 14 (2008), 411–426.CrossRefGoogle Scholar
Boccardo, L. and Orsina, L.. Semilinear elliptic equations with singular nonlinearities. Calc. Var. Part. Diff. Equ. 37 (2010), 363–380.CrossRefGoogle Scholar
Canino, A., Esposito, F. and Sciunzi, B.. On the Höpf boundary lemma for singular semilinear elliptic equations. J. Diff. Equ. 266 (2019), 5488–5499.CrossRefGoogle Scholar
Cîrstea, F. and Rǎdulescu, V. D.. Uniqueness of the blow-up boundary solution of logistic equations with absorbtion. C. R. Acad. Sci. Paris, Sér. I 335 (2002), 447–452.CrossRefGoogle Scholar
Coclite, M. M. and Palmieri, G.. On a singular nonlinear Dirichlet problem. Commun. Part. Diff. Eq. 14 (1989), 1315–1327.CrossRefGoogle Scholar
Crandall, M. G., Rabinowitz, P. H. and Tartar, L.. On a Dirichlet problem with a singular nonlinearity. Commun. Part. Diff. Equ. 2 (1977), 193–222.CrossRefGoogle Scholar
Cuccu, F., Giarrusso, E. and Porru, G.. Boundary behaviour for solutions of elliptic singular equations with a gradient term. Nonlinear Anal. 69 (2008), 4550–4566.CrossRefGoogle Scholar
Cui, S.. Existence and nonexistence of positive solutions for singular semilinear elliptic boundary value problems. Nonlinear Anal. 41 (2000), 149–176.CrossRefGoogle Scholar
Fulks, W. and Maybee, J. S.. A singular nonlinear elliptic equation. Osaka J. Math. 12 (1960), 1–19.Google Scholar
Ghergu, M., Rǎdulescu, V. D.. Singular elliptic problems: bifurcation and asymptotic analysis. (Oxford: Oxford University Press, 2008).Google Scholar
Giarrusso, E., Porru, G.. Boundary behaviour of solutions to nonlinear elliptic singular problems. In Applicable mathematics in the golden age (ed. Misra, J. C.), pp. 163–178 (New Delhi, India: Narosa Publishing House, 2003).Google Scholar
Giarrusso, E. and Porru, G.. Problems for elliptic singular equations with a gradient term. Nonlinear Anal. 65 (2006), 107–128.CrossRefGoogle Scholar
Gomes, S. M.. On a singular nonlinear elliptic problem. SIAM J. Math. Anal. 17 (1986), 1359–1369.CrossRefGoogle Scholar
Gontara, S., Mâagli, H., Masmoudi, S. and Turki, S.. Asymptotic behavior of positive solutions of a singular nonlinear Dirichlet problem. J. Math. Anal. Appl. 369 (2010), 719–729.CrossRefGoogle Scholar
Gui, C. and Lin, F. H.. Regularity of an elliptic problem with a singular nonlinearity. Proc. R. Soc. Edinburgh 123A (1993), 1021–1029.CrossRefGoogle Scholar
Lair, A. V. and Shaker, A. W.. Classical and weak solutions of a singular elliptic problem. J. Math. Anal Appl. 211 (1997), 371–385.CrossRefGoogle Scholar
Lazer, A. C. and McKenna, P. J.. On a singular elliptic boundary value problem. Proc. Amer. Math. Soc. 111 (1991), 721–730.CrossRefGoogle Scholar
Mohammed, A.. Positive solutions of the p-Laplace equation with singular nonlinearity. J. Math. Anal. Appl. 352 (2009), 234–245.CrossRefGoogle Scholar
Nachman, A. and Callegari, A.. A nonlinear singular boundary value problem in the theory of pseudoplastic fluids. SIAM J. Appl. Math. 38 (1980), 275–281.CrossRefGoogle Scholar
del Pino, M.. A global estimate for the gradient in a singular elliptic boundary value problem. Proc. R. Soc. Edinburgh Sect. A 122 (1992), 341–352.CrossRefGoogle Scholar
Porru, G. and Vitolo, A.. Problems for elliptic singular equations with a quadratic gradient term. J. Math. Anal. Appl. 334 (2007), 467–486.CrossRefGoogle Scholar
Seneta, R.. Regular varying functions. Lecture Notes in Mathematics, vol. 508 (Berlin · Heidelberg · New York: Springer-Verlag, 1976).CrossRefGoogle Scholar
Shi, J. and Yao, M.. On a singular semiinear elliptic problem. Proc. R. Soc. Edinburgh 128A (1998), 1389–1401.CrossRefGoogle Scholar
Stuart, C. A.. Existence and approximation of solutions of nonlinear elliptic equations. Math. Z. 147 (1976), 53–63.CrossRefGoogle Scholar
Sun, Y. and Zhang, D.. The role of the power 3 for elliptic equations with negative exponents. Calc. Var. Part. Diff. Equ. 49 (2014), 909–922.Google Scholar
Zeddini, N., Alsaedi, R. and Mâagli, H.. Exact boundary behavior of the unique positive solution to some singular elliptic problems. Nonlinear Anal. 89 (2013), 146–156.CrossRefGoogle Scholar
Zhang, Z. and Yu, J.. On a singular nonlinear Dirichlet problem with a convection term. SIAM J. Math. Anal. 32 (2000), 916–927.CrossRefGoogle Scholar
Zhang, Z. and Chen, J.. Existence and optimal estimates of solutions for singular nonlinear Dirichlet problems. Nonlinear Anal. 57 (2004), 473–484.CrossRefGoogle Scholar
Zhang, Z.. The asymptotic behaviour of the unique solution for the singular Lane–Emden–Fowler equations. J. Math. Anal. Appl. 312 (2005), 33–43.CrossRefGoogle Scholar
Zhang, Z.. Boundary behavior of solutions to some singular elliptic boundary value problems. Nonlinear Anal. 69 (2008), 2293–2302.CrossRefGoogle Scholar
Zhang, Z., Li, X. and Zhao, Y.. Boundary behavior of solutions to singular boundary value problems for nonlinear elliptic equations. Adv. Nonlinear Stud. 10 (2010), 249–261.CrossRefGoogle Scholar
Zhang, Z., Li, X. and Li, B.. The exact boundary behavior of the unique solution to a singular Dirichlet problem with a nonlinear convection term. Nonlinear Anal. 108 (2014), 14–28.CrossRefGoogle Scholar
Zhang, Z., Li, X. and Li, B.. The exact boundary behavior of solutions to singular nonlinear Lane-Emden-Fowler type boundary value problems. Nonlinear Anal., Real World Appl. 21 (2015), 34–52.CrossRefGoogle Scholar
Zhang, Z.. Two classes of nonlinear singular Dirichlet problems with natural growth: existence and asymptotic behavior. Adv. Nonlinear Stud. 20 (2020), 77–93.CrossRefGoogle Scholar