Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T09:44:22.792Z Has data issue: false hasContentIssue false
  • English
  • Français

On the relaxation of integral functionals depending on the symmetrized gradient

Part of: Existence theories

Published online by Cambridge University Press:  08 April 2020

Kamil Kosiba  and
Filip Rindler
Kamil Kosiba
Affiliation:
Mathematics Institute, University of Warwick, CoventryCV4 7AL, UK ([email protected])
Filip Rindler
Affiliation:
Mathematics Institute, University of Warwick, CoventryCV4 7AL, UK and The Alan Turing Institute, British Library, 96 Euston Road, LondonNW1 2DB, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove results on the relaxation and weak* lower semicontinuity of integral functionals of the form

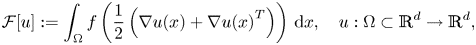$${\cal F}[u]: = \int_\Omega f \left( {\displaystyle{1 \over 2}\left( {\nabla u(x) + \nabla u{(x)}^T} \right)} \right) \,{\rm d}x,\quad u:\Omega \subset {\mathbb R}^d\to {\mathbb R}^d,$$
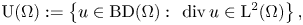over the space BD(Ω) of functions of bounded deformation or over the Temam–Strang space
$${\rm U}(\Omega ): = \left\{ {u\in {\rm BD}(\Omega ):\;\,{\rm div}\,u\in {\rm L}^2(\Omega )} \right\},$$
depending on the growth and shape of the integrand f. Such functionals are interesting, for example, in the study of Hencky plasticity and related models.

Keywords

Relaxationlower semicontinuityintegral functionalsfunctions of bounded deformationHencky plasticity

MSC classification

Primary: 49J45: Methods involving semicontinuity and convergence; relaxation
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 2 , April 2021 , pp. 473 - 508
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alberti, G.. Rank one property for derivatives of functions with bounded variation. Proc. Roy. Soc. Edinburgh Sect. A 123 (1993), 239–274.CrossRefGoogle Scholar
2Ambrosio, L., Coscia, A. and Dal Maso, G.. Fine properties of functions with bounded deformation. Arch. Ration. Mech. Anal. 139 (1997), 201–238.CrossRefGoogle Scholar
3Ambrosio, L. and Dal Maso, G.. On the relaxation in BV(Ω; R m) of quasi-convex integrals. J. Funct. Anal. 109 (1992), 76–97.CrossRefGoogle Scholar
4Ambrosio, L., Fusco, N. and Pallara, D.. Functions of bounded variation and free-discontinuity problems. Oxford Mathematical Monographs (New York: Oxford University Press, 2000).Google Scholar
5Anzellotti, G. and Giaquinta, M.. Existence of the displacements field for an elasto-plastic body subject to Hencky's law and Von Mises yield condition. Manuscripta Math. 32 (1980), 101–136.CrossRefGoogle Scholar
6Arroyo-Rabasa, A., De Philippis, G. and Rindler, F.. Lower semicontinuity and relaxation of linear-growth integral functionals under PDE constraints. In Advances in calculus of variations (2017), https://www.degruyter.com/view/journals/acv/ahead-of-print/article-10.1515-acv-2017-0003/article-10.1515-acv-2017-0003.xml.Google Scholar
7Attouch, H., Buttazzo, G. and Michaille, G.. Variational analysis in Sobolev and BV spaces: applications to PDEs and optimization (Philadelphia, PA: SIAM, 2014).CrossRefGoogle Scholar
8Barroso, A. C., Fonseca, I. and Toader, R.. A relaxation theorem in the space of functions of bounded deformation. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 29 (2000), 19–49.Google Scholar
9Bogovskii, M. E.. Solution of the first boundary value problem for an equation of continuity of an incompressible medium. Dokl. Akad. Nauk SSSR 248 (1979), 1037–1040.Google Scholar
10Bogovskii, M. E.. Solutions of some problems of vector analysis, associated with the operators div and grad. In Theory of cubature formulas and the application of functional analysis to problems of mathematical physics, vol. 1980 of Trudy Sem. S. L. Soboleva, No. 1, pp. 5–40, 149 (Akad. Nauk SSSR Sibirsk. Otdel., Inst. Mat., Novosibirsk, 1980).Google Scholar
11Bojarski, J.. The relaxation of Signorini problems in Hencky plasticity. I. Three-dimensional solid. Nonlinear Anal. 29 (1997), 1091–1116.CrossRefGoogle Scholar
12Bojarski, J.. The relaxation of Signorini problems in Hencky plasticity. II. Plates. Nonlinear Anal. 29 (1997), 1117–1143.CrossRefGoogle Scholar
13Braides, A., Defranceschi, A. and Vitali, E.. A relaxation approach to Hencky's plasticity. Appl. Math. Optim. 35 (1997), 45–68.Google Scholar
14Conti, S. and Ortiz, M.. Dislocation microstructures and the effective behavior of single crystals. Arch. Rational Mech. Anal. 176 (2005), 103–147.CrossRefGoogle Scholar
15Dacorogna, B.. Direct methods in the calculus of variations, 2nd edn, Applied Mathematical Sciences, vol. 78 (New York: Springer, 2008).Google Scholar
16De Philippis, G. and Rindler, F.. On the structure of $\mathcal {A}$-free measures and applications. Ann. Math. 184 (2016), 1017–1039.CrossRefGoogle Scholar
17De Philippis, G. and Rindler, F.. Characterization of generalized Young measures generated by symmetric gradients. Arch. Ration. Mech. Anal. 224 (2017), 1087–1125.CrossRefGoogle Scholar
18Fonseca, I. and Müller, S.. Relaxation of quasiconvex functionals in BV(Ω, R p) for integrands f(x, u, ∇ u). Arch. Ration. Mech. Anal. 123 (1993), 1–49.CrossRefGoogle Scholar
19Fonseca, I. and Müller, S.. $\mathcal {A}$-Quasiconvexity, lower semicontinuity, and Young measures. SIAM J. Math. Anal. 30 (1999), 1355–1390.CrossRefGoogle Scholar
20Fuchs, M. and Seregin, G.. Variational methods for problems from plasticity theory and for generalized Newtonian fluids, Lecture Notes in Mathematics, vol. 1749 (Berlin: Springer-Verlag, 2000).CrossRefGoogle Scholar
21Galdi, G. P.. An introduction to the mathematical theory of the Navier-Stokes equations: steady-state problems, 2nd edn, Springer Monographs in Mathematics (New York: Springer, 2011).CrossRefGoogle Scholar
22Jesenko, M. and Schmidt, B.. Homogenization and the limit of vanishing hardening in Hencky plasticity with non-convex potentials. Calc. Var. Partial Differ. Equ. 57 (2018), Art. 2, 43.CrossRefGoogle Scholar
23Kirchheim, B. and Kristensen, J.. Automatic convexity of rank-1 convex functions. C. R. Math. 349 (2011), 407–409.CrossRefGoogle Scholar
24Kirchheim, B. and Kristensen, J.. On rank-one convex functions that are homogeneous of degree one. Arch. Ration. Mech. Anal. 221 (2016), 527–558.CrossRefGoogle Scholar
25Kohn, R. V.. New integral estimates for deformations in terms of their nonlinear strains. Arch. Ration. Mech. Anal. 78 (1982), 131–172.CrossRefGoogle Scholar
26Kristensen, J. and Rindler, F.. Characterization of generalized gradient Young measures generated by sequences in W1,1 and BV. Arch. Ration. Mech. Anal. 197 (2010), 539–598. Erratum: 203 (2012), 693–700.CrossRefGoogle Scholar
27Kristensen, J. and Rindler, F.. Relaxation of signed integral functionals in BV. Calc. Var. Partial Differ. Equ. 37 (2010), 29–62.CrossRefGoogle Scholar
28Müller, S.. On quasiconvex functions which are homogeneous of degree 1. Indiana Univ. Math. J. 41 (1992), 295–301.CrossRefGoogle Scholar
29Massaccesi, A. and Vittone, D.. An elementary proof of the rank one theorem for BV functions. Preprint, 2016.Google Scholar
30Matthies, H., Strang, G. and Christiansen, E.. The saddle point of a differential program. In Energy methods in finite element analysis, pp. 309–318 (Chichester: Wiley, 1979).Google Scholar
31Mora, M. G.. Relaxation of the Hencky model in perfect plasticity. J. Math. Pures Appl. (9) 106 (2016), 725–743.CrossRefGoogle Scholar
32Morrey, C. B. Jr., Quasiconvexity and the semicontinuity of multiple integrals. Pac. J. Math. 2 (1952), 25–53.CrossRefGoogle Scholar
33Rindler, F.. Lower semicontinuity for integral functionals in the space of functions of bounded deformation via rigidity and Young measures. Arch. Ration. Mech. Anal. 202 (2011), 63–113.CrossRefGoogle Scholar
34Rindler, F.. Calculus of variations, Universitext (Cham: Springer, 2018).CrossRefGoogle Scholar
35Suquet, P.-M.. Existence et régularité des solutions des équations de la plasticité. C. R. Acad. Sci. Paris Sér. A 286 (1978), 1201–1204.Google Scholar
36Suquet, P.-M.. Un espace fonctionnel pour les équations de la plasticité. Ann. Fac. Sci. Toulouse Math. 1 (1979), 77–87.CrossRefGoogle Scholar
37Temam, R.. Problèmes mathématiques en plasticité (Montrouge Gauthier-Villars, 1985).Google Scholar
38Temam, R. and Strang, G.. Functions of bounded deformation. Arch. Ration. Mech. Anal. 75 (1980), 7–21.CrossRefGoogle Scholar