Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T11:30:00.618Z Has data issue: false hasContentIssue false
  • English
  • Français

On decay rates of the solutions of parabolic Cauchy problems

Part of: Miscellaneous applications of functional analysis Parabolic equations and systems Normed linear spaces and Banach spaces; Banach lattices Partial differential equations

Published online by Cambridge University Press:  21 July 2020

José Bonet ,
Wolfgang Lusky  and
Jari Taskinen
José Bonet
Affiliation:
Instituto Universitario de Matemática Pura y Aplicada IUMPA, Universitat Politécnica de Valéncia, ValenciaE-46071, Spain ([email protected])
Wolfgang Lusky
Affiliation:
Institut für Mathematik, Universität Paderborn, PaderbornD-33098, Germany ([email protected])
Jari Taskinen
Affiliation:
Department of Mathematics and Statistics, P.O. Box 68, University of Helsinki, Helsinki00014, Finland ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Cauchy problem for a general class of parabolic partial differential equations in the Euclidean space ℝN. We show that given a weighted Lp-space 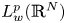$L_w^p({\mathbb {R}}^N)$ with 1 ⩽ p < ∞ and a fast growing weight w, there is a Schauder basis 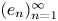$(e_n)_{n=1}^\infty$ in 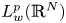$L_w^p({\mathbb {R}}^N)$ with the following property: given an arbitrary positive integer m there exists nm > 0 such that, if the initial data f belongs to the closed linear span of en with n ⩾ nm, then the decay rate of the solution of the problem is at least t−m for large times t.

The result generalizes the recent study of the authors concerning the classical linear heat equation. We present variants of the result having different methods of proofs and also consider finite polynomial decay rates instead of unlimited m.

Keywords

Parabolic PDECauchy problemBanach spaceSchauder basisdecay rate

MSC classification

Primary: 35K05: Heat equation
Secondary: 35B40: Asymptotic behavior of solutions 46B15: Summability and bases 46N20: Applications to differential and integral equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 3 , June 2021 , pp. 1021 - 1039
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonet, J., Lusky, W. and Taskinen, J.. Schauder bases and the decay rate of the heat equation. J. Evolution Eq. 19 (2019), 717–728.CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N.. Elliptic partial differential equations of second order (Berlin-Heidelberg: Springer-Verlag, 2001).CrossRefGoogle Scholar
Howard, P.. Linear stability for transition front solutions in multidimensional Cahn-Hilliard systems. J.Dyn. Diff. Equat. 29 (2017), 895–955.CrossRefGoogle Scholar
Ladyszenskaya, O.. The boundary value problems in mathematical physics (New York-Berlin-Heidelberg-Tokyo: Springer-Verlag, 1985).CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L.. Classical Banach spaces I (Berlin: Springer-Verlag, 1977).CrossRefGoogle Scholar
Nečas, J.. Direct methods in the theory of elliptic equations. Springer Monographs in Mathematics. (Heidelberg: Springer, 2012).CrossRefGoogle Scholar
Pazy, A.. Semigroups of linear operators and applications to partial differential equations (New York: Springer-Verlag, 1983).CrossRefGoogle Scholar
Rudin, W.. Functional analysis, 2nd edn (New York: McGraw-Hill Science/Engineering/ Math, 1991).Google Scholar
Wojtaszyck, P.. Banach spaces for analysts. Cambridge studies in advanced mathematics vol. 25, (Cambridge: Cambridge University Press, 1991).CrossRefGoogle Scholar