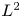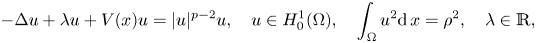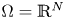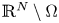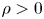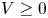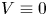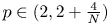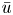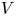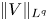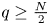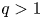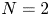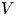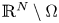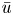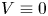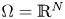1. Introduction and main results
In this paper, we study a class of problems of the form

where $\Omega =\mathbb {R}^N$![]() or $\Omega$
or $\Omega$![]() is an exterior domain, that is $\mathbb {R}^N\setminus \Omega$
is an exterior domain, that is $\mathbb {R}^N\setminus \Omega$![]() is a compact set, $N\ge 1$
is a compact set, $N\ge 1$![]() , $V$
, $V$![]() is a given potential and $2< p<2+4/N$
is a given potential and $2< p<2+4/N$![]() , namely the nonlinearity is superlinear and mass-subcritical. Here $\lambda$
, namely the nonlinearity is superlinear and mass-subcritical. Here $\lambda$![]() will arise as a Lagrange multiplier related to the mass constraint $\|u\|_{L^2}=\rho >0$
will arise as a Lagrange multiplier related to the mass constraint $\|u\|_{L^2}=\rho >0$![]() . We will focus on potentials that verify
. We will focus on potentials that verify

Problems of the form (P) arise from the nonlinear Schrödinger and Klein-Gordon equations
where $\Phi :\mathbb {R}^N\times (0,+\infty )\to \mathbb {C}$![]() . If $f(r e^{i\theta })=f(r)e^{i\theta }$
. If $f(r e^{i\theta })=f(r)e^{i\theta }$![]() , $r,\theta \in \mathbb {R}$
, $r,\theta \in \mathbb {R}$![]() , then one can look for standing wave solutions of (S) and (KG), namely solutions of the form
, then one can look for standing wave solutions of (S) and (KG), namely solutions of the form
where $u$![]() is a real function. In the model case $f(\Phi )=|\Phi |^{p-2}\Phi$
is a real function. In the model case $f(\Phi )=|\Phi |^{p-2}\Phi$![]() we consider, $u$
we consider, $u$![]() has to solve the equation in (P). We refer the reader to [Reference Berestycki and Lions8–Reference Cazenave and Lions10] for more detailed physical motivations.
has to solve the equation in (P). We refer the reader to [Reference Berestycki and Lions8–Reference Cazenave and Lions10] for more detailed physical motivations.
If the frequency $\lambda$![]() in ansatz (1.2) is fixed, and we consider the pure power model case with $p\in (2,2^*)$
in ansatz (1.2) is fixed, and we consider the pure power model case with $p\in (2,2^*)$![]() , where $2^*=\frac {2N}{(N-2)^+}$
, where $2^*=\frac {2N}{(N-2)^+}$![]() , then looking for solutions of (S) and (KG) corresponds to looking for critical points of the action functional
, then looking for solutions of (S) and (KG) corresponds to looking for critical points of the action functional
A very large number of works are devoted to this unconstrained problem, we only refer the reader to [Reference Ambrosetti and Malchiodi2, Reference Cerami11, Reference Struwe39] for a survey on almost classical results, and to the recent papers [Reference Devillanova and Solimini16, Reference Molle and Passaseo33] and references therein for new contributions.
Another point of view is to fix a priori the $L^2$![]() norm of the solution. This point of view is particularly relevant because this quantity (the mass or the charge of the particle) is preserved along the time evolution. In this case, the solutions $u$
norm of the solution. This point of view is particularly relevant because this quantity (the mass or the charge of the particle) is preserved along the time evolution. In this case, the solutions $u$![]() correspond to the critical points of the energy functional
correspond to the critical points of the energy functional
constrained on
and the frequency $\lambda$![]() arises as a Lagrange multiplier. Even if this fixed mass problem is classic (see for example [Reference Cazenave and Lions10]), only in the last decade it has been studied extensively and, in particular, very little has been done in the non-autonomous case (see [Reference Alves and Ji1, Reference Bartsch and de Valeriola5, Reference Bartsch, Molle, Rizzi and Verzini6, Reference Ikoma and Miyamoto24–Reference Jeanjean and Lu26, Reference Molle, Riey and Verzini34, Reference Zhang and Zhang41] and references therein).
arises as a Lagrange multiplier. Even if this fixed mass problem is classic (see for example [Reference Cazenave and Lions10]), only in the last decade it has been studied extensively and, in particular, very little has been done in the non-autonomous case (see [Reference Alves and Ji1, Reference Bartsch and de Valeriola5, Reference Bartsch, Molle, Rizzi and Verzini6, Reference Ikoma and Miyamoto24–Reference Jeanjean and Lu26, Reference Molle, Riey and Verzini34, Reference Zhang and Zhang41] and references therein).
We refer the reader to [Reference Dovetta, Serra and Tilli17] for a recent analysis on the connections between the fixed mass and the fixed frequency points of view (see also [Reference Noris, Tavares and Verzini35] and references therein).
If $2+\frac 4N< p<2^*$![]() , the so called mass-supercritical regime, then $E$
, the so called mass-supercritical regime, then $E$![]() is not bounded from below on $S_\rho$
is not bounded from below on $S_\rho$![]() , as follows by evaluating the functional over the fibres on $S_\rho$
, as follows by evaluating the functional over the fibres on $S_\rho$![]() of the type $u_t:=t^{N/2} u_1(t\cdot )$
of the type $u_t:=t^{N/2} u_1(t\cdot )$![]() , for fixed $u_1\in S_\rho$
, for fixed $u_1\in S_\rho$![]() and $t>0$
and $t>0$![]() . So the problem cannot be addressed by minimization. Jeanjean in the pioneering paper [Reference Jeanjean25] analysed the autonomous problem, for more general mass-supercritical nonlinearities, and he recognized a mountain pass structure, related to the above-introduced fibres. The method developed in [Reference Jeanjean25] does not work in the non-autonomous case, even if the potential is radially symmetric. The non-autonomous case in the mass-supercritical regime has been studied in [Reference Bartsch, Molle, Rizzi and Verzini6, Reference Molle, Riey and Verzini34], for not necessarily symmetrical potentials. In [Reference Bartsch, Molle, Rizzi and Verzini6], the authors found a mountain-pass solution if $V\ge 0$
. So the problem cannot be addressed by minimization. Jeanjean in the pioneering paper [Reference Jeanjean25] analysed the autonomous problem, for more general mass-supercritical nonlinearities, and he recognized a mountain pass structure, related to the above-introduced fibres. The method developed in [Reference Jeanjean25] does not work in the non-autonomous case, even if the potential is radially symmetric. The non-autonomous case in the mass-supercritical regime has been studied in [Reference Bartsch, Molle, Rizzi and Verzini6, Reference Molle, Riey and Verzini34], for not necessarily symmetrical potentials. In [Reference Bartsch, Molle, Rizzi and Verzini6], the authors found a mountain-pass solution if $V\ge 0$![]() is suitably small, while [Reference Molle, Riey and Verzini34] concerns the case $V\le 0$
is suitably small, while [Reference Molle, Riey and Verzini34] concerns the case $V\le 0$![]() and the existence of two solutions is proved when $V$
and the existence of two solutions is proved when $V$![]() is suitably small and the operator $-\Delta +V$
is suitably small and the operator $-\Delta +V$![]() is not positive-definite.
is not positive-definite.
In the mass-subcritical regime $2< p<2+\frac 4N$![]() , the functional $E$
, the functional $E$![]() is bounded from below on $S_\rho$
is bounded from below on $S_\rho$![]() by the Gagliardo-Nirenberg inequality (see (3.4), (3.5)). Ikoma e Miyamoto in [Reference Ikoma and Miyamoto24] considered more general non-autonomous problems of the type
by the Gagliardo-Nirenberg inequality (see (3.4), (3.5)). Ikoma e Miyamoto in [Reference Ikoma and Miyamoto24] considered more general non-autonomous problems of the type
where $\Omega =\mathbb {R}^N$![]() , and the nonlinearity $f(x,u)=f(u)$
, and the nonlinearity $f(x,u)=f(u)$![]() has sub-linear growth in 0 and mass-subcritical growth at infinity, that is
has sub-linear growth in 0 and mass-subcritical growth at infinity, that is
If the shape of the potential is $V\le 0$![]() and $V(x)\to 0$
and $V(x)\to 0$![]() as $|x|\to \infty$
as $|x|\to \infty$![]() , and both $f$
, and both $f$![]() and $V$
and $V$![]() satisfy various technical assumptions, then the authors prove, by concentration-compactness arguments, that there exists $\rho _0>0$
satisfy various technical assumptions, then the authors prove, by concentration-compactness arguments, that there exists $\rho _0>0$![]() such that the energy functional related to (1.3) has a global minimum in $S_\rho$
such that the energy functional related to (1.3) has a global minimum in $S_\rho$![]() for $\rho >\rho _0$
for $\rho >\rho _0$![]() , and the global minimum is not attained if $0<\rho <\rho _0$
, and the global minimum is not attained if $0<\rho <\rho _0$![]() . Moreover, some sufficient conditions on $f$
. Moreover, some sufficient conditions on $f$![]() and $V$
and $V$![]() are provided to get $\rho _0=0$
are provided to get $\rho _0=0$![]() .
.
In the more recent paper [Reference Alves and Ji1], Alves and Ji considered in problem (P) some classes of potentials $V$![]() where a global minimum for $E$
where a global minimum for $E$![]() on $S_\rho$
on $S_\rho$![]() exists, for suitable $\rho$
exists, for suitable $\rho$![]() . Namely, in [Reference Alves and Ji1] the authors work on potentials $V$
. Namely, in [Reference Alves and Ji1] the authors work on potentials $V$![]() , not required vanishing at infinity, that verify one of these assumptions: $(V_1)$
, not required vanishing at infinity, that verify one of these assumptions: $(V_1)$![]() $\inf _{\mathbb {R}^N} V<\liminf _{|x|\to \infty }V(x)$
$\inf _{\mathbb {R}^N} V<\liminf _{|x|\to \infty }V(x)$![]() , $(V_2)$
, $(V_2)$![]() there exists $\mu _0>0$
there exists $\mu _0>0$![]() such that $\mathop {\rm meas}\nolimits \{V>\mu _0\}<\infty$
such that $\mathop {\rm meas}\nolimits \{V>\mu _0\}<\infty$![]() and $\mathop {\rm int}\nolimits (V^{-1}(0))\neq \emptyset$
and $\mathop {\rm int}\nolimits (V^{-1}(0))\neq \emptyset$![]() , $(V_3)$
, $(V_3)$![]() $V$
$V$![]() is 1-periodic in each variable, $(V_4)$
is 1-periodic in each variable, $(V_4)$![]() $V$
$V$![]() is asymptotically 1-periodic, that is there exists a 1-periodic function $V_p:\mathbb {R}^N\to \mathbb {R}$
is asymptotically 1-periodic, that is there exists a 1-periodic function $V_p:\mathbb {R}^N\to \mathbb {R}$![]() such that
such that
After submitting this paper, the interesting works [Reference Song37, Reference Yang, Qi and Zou40] have been brought to our attention. In those papers, non homogeneous nonlinearities as in (1.3) are studied.
Yang, Qi and Zou in [Reference Yang, Qi and Zou40] improve the result of [Reference Ikoma and Miyamoto24]. They consider problem (1.3) with $\Omega =\mathbb {R}^N$![]() , $V(x)\le \lim _{|x|\to \infty }V(x)=:V_\infty \in (-\infty,+\infty ]$
, $V(x)\le \lim _{|x|\to \infty }V(x)=:V_\infty \in (-\infty,+\infty ]$![]() and $f\in {\mathcal{C}}(\Omega \times \mathbb {R},\mathbb {R})$
and $f\in {\mathcal{C}}(\Omega \times \mathbb {R},\mathbb {R})$![]() satisfies Berestycki-Lions type conditions with mass-subcritical growth. Moreover, some technical assumptions used in [Reference Ikoma and Miyamoto24] are removed. In the coercive case $V_\infty =+\infty$
satisfies Berestycki-Lions type conditions with mass-subcritical growth. Moreover, some technical assumptions used in [Reference Ikoma and Miyamoto24] are removed. In the coercive case $V_\infty =+\infty$![]() , the existence of a ground state solution is proved for every $\rho >0$
, the existence of a ground state solution is proved for every $\rho >0$![]() , while for $V_\infty <+\infty$
, while for $V_\infty <+\infty$![]() the authors show that still $\rho _0\ge 0$
the authors show that still $\rho _0\ge 0$![]() exists such that there is a ground state solution for $\rho >\rho _0$
exists such that there is a ground state solution for $\rho >\rho _0$![]() and it does not exist for $0<\rho <\rho _0$
and it does not exist for $0<\rho <\rho _0$![]() .
.
Some results in [Reference Song37] concern symmetric exterior domains in some mass-supercritical regimes. Therein, Song studies (1.3) when $\Omega$![]() is a bounded starshaped domain or the complementary of a ball in $\mathbb {R}^N$
is a bounded starshaped domain or the complementary of a ball in $\mathbb {R}^N$![]() with $N\ge 2$
with $N\ge 2$![]() , $V\equiv 0$
, $V\equiv 0$![]() and $f\in {\mathcal{C}}^1(\Omega \times \mathbb {R},\mathbb {R})$
and $f\in {\mathcal{C}}^1(\Omega \times \mathbb {R},\mathbb {R})$![]() is a superlinear and mass-supercritical nonlinearity. When $\Omega$
is a superlinear and mass-supercritical nonlinearity. When $\Omega$![]() is the complementary of a ball and $f(\cdot,u)$
is the complementary of a ball and $f(\cdot,u)$![]() is radially symmetric, the author proves that there exists a sequence $((\lambda _k,u_k))_k$
is radially symmetric, the author proves that there exists a sequence $((\lambda _k,u_k))_k$![]() in $H^1_0(\Omega )\times \mathbb {R}$
in $H^1_0(\Omega )\times \mathbb {R}$![]() of solutions of (1.3)(eq) such that $\lambda _k\to 0$
of solutions of (1.3)(eq) such that $\lambda _k\to 0$![]() and $|u_k|_2\to \infty$
and $|u_k|_2\to \infty$![]() , while there exists no sequence $((\lambda _k,u_k))_k$
, while there exists no sequence $((\lambda _k,u_k))_k$![]() in $H^1_0(\Omega )\times \mathbb {R}$
in $H^1_0(\Omega )\times \mathbb {R}$![]() of solutions of (1.3)(eq) such that $\lambda _k\to 0$
of solutions of (1.3)(eq) such that $\lambda _k\to 0$![]() and $|u_k|_2\to 0$
and $|u_k|_2\to 0$![]() . Moreover, if (1.3)(eq) has at most one positive radial solution in $H^1_0(\Omega )$
. Moreover, if (1.3)(eq) has at most one positive radial solution in $H^1_0(\Omega )$![]() for every $\lambda >0$
for every $\lambda >0$![]() , then (1.3) has a positive radial solution for large $\rho$
, then (1.3) has a positive radial solution for large $\rho$![]() .
.
Here, we are concerned with the mass-subcritical case when $V\ge 0$![]() so no minimum solution exists, up to the autonomous case $V\equiv 0$
so no minimum solution exists, up to the autonomous case $V\equiv 0$![]() and $\Omega =\mathbb {R}^N$
and $\Omega =\mathbb {R}^N$![]() (see proposition 1.4). Moreover, we focus on domains that can be not only $\mathbb {R}^N$
(see proposition 1.4). Moreover, we focus on domains that can be not only $\mathbb {R}^N$![]() but also general exterior domains, answering the question raised in [Reference Molle, Riey and Verzini34] for mass-supercritical problems, whether the existence of bound state solutions can be treated in exterior domains as in the whole space. To the best of our knowledge, these issues are only partially addressed in previous papers. About exterior domains in the mass-subcritical case, it is worth mentioning [Reference Zhang and Zhang41], where the authors consider the autonomous problem $V\equiv 0$
but also general exterior domains, answering the question raised in [Reference Molle, Riey and Verzini34] for mass-supercritical problems, whether the existence of bound state solutions can be treated in exterior domains as in the whole space. To the best of our knowledge, these issues are only partially addressed in previous papers. About exterior domains in the mass-subcritical case, it is worth mentioning [Reference Zhang and Zhang41], where the authors consider the autonomous problem $V\equiv 0$![]() in dimension $N\ge 3$
in dimension $N\ge 3$![]() and they found the existence of a bound state solution if the size of ‘hole’ $\mathbb {R}^N\setminus \Omega$
and they found the existence of a bound state solution if the size of ‘hole’ $\mathbb {R}^N\setminus \Omega$![]() is small.
is small.
The main results are the following:
Theorem 1.1 Let $N\ge 2,$![]() $\Omega =\mathbb {R}^N$
$\Omega =\mathbb {R}^N$![]() or $\mathbb {R}^N\setminus \Omega$
or $\mathbb {R}^N\setminus \Omega$![]() compact, $\rho >0$
compact, $\rho >0$![]() . If $V$
. If $V$![]() satisfies (1.1) and
satisfies (1.1) and
where
(see (2.5) for the constant $\lambda _1$![]() ), then there exists a solution $(\lambda,\bar u)$
), then there exists a solution $(\lambda,\bar u)$![]() of (P) such that $\lambda >0$
of (P) such that $\lambda >0$![]() and $\bar u\ge 0$
and $\bar u\ge 0$![]() .
.
Theorem 1.2 Let $N\ge 2$![]() , $\Omega =\mathbb {R}^N$
, $\Omega =\mathbb {R}^N$![]() or $\mathbb {R}^N\setminus \Omega$
or $\mathbb {R}^N\setminus \Omega$![]() compact, $\rho >0$
compact, $\rho >0$![]() . There exists $L =L(q,\Omega,\rho )>0$
. There exists $L =L(q,\Omega,\rho )>0$![]() such that if $V$
such that if $V$![]() satisfies (1.1), with
satisfies (1.1), with
and $\|V\|_{q}< L$![]() , then problem (P) has a solution $(\lambda,\bar u)$
, then problem (P) has a solution $(\lambda,\bar u)$![]() , verifying $\lambda >0$
, verifying $\lambda >0$![]() and $\bar u\ge 0$
and $\bar u\ge 0$![]() .
.
The case $N = 1$![]() has its own specificity and will be dealt with in § 6.
has its own specificity and will be dealt with in § 6.
A priori, a nonnegative solution $\bar u$![]() of (P) belongs to $H^1(\Omega )$
of (P) belongs to $H^1(\Omega )$![]() , so we cannot say that $\bar u>0$
, so we cannot say that $\bar u>0$![]() , $\forall x\in \Omega$
, $\forall x\in \Omega$![]() . Anyway, under mild assumptions, $\bar u$
. Anyway, under mild assumptions, $\bar u$![]() turns out to be sufficiently regular to apply the Harnack inequality and therefore to be pointwise positive. In the following proposition, we collect some regularity properties. Its proof is almost standard, so we only outline it in the appendix.
turns out to be sufficiently regular to apply the Harnack inequality and therefore to be pointwise positive. In the following proposition, we collect some regularity properties. Its proof is almost standard, so we only outline it in the appendix.
Proposition 1.3 Let $\bar u$![]() be a solution of (P). If $N\ge 2$
be a solution of (P). If $N\ge 2$![]() , then
, then
(a) if $V\in L^q_{\mathop {\rm loc}\nolimits }(\Omega )$
 for some $q>\frac N2,$
for some $q>\frac N2,$ then $\bar u\in {\mathcal{C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$
then $\bar u\in {\mathcal{C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$ , and if $\bar u$
, and if $\bar u$ is nonnegative then $\bar u(x)>0$
is nonnegative then $\bar u(x)>0$ $\forall x\in \Omega$
$\forall x\in \Omega$ ;
;(b) if $V\in L^q_{\mathop {\rm loc}\nolimits }(\Omega )$
 for some $q> N,$
for some $q> N,$ then $\bar u\in {\mathcal{C}}^{1,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$
then $\bar u\in {\mathcal{C}}^{1,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$ ;
;(c) if $V\in {\mathcal{C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega ),$
 then $\bar u\in {\mathcal{C}}^2(\Omega )$
then $\bar u\in {\mathcal{C}}^2(\Omega )$ and it is a classical solution.
and it is a classical solution.
If $N=1,$![]() then
then
(d) if $V\in L^1_{\mathop {\rm loc}\nolimits }(\Omega ),$
 then $\bar u$
then $\bar u$ is continuously differentiable and if $\bar u$
is continuously differentiable and if $\bar u$ is nonnegative then $\bar u(x)>0$
is nonnegative then $\bar u(x)>0$ $\forall x\in \Omega$
$\forall x\in \Omega$ ;
;(e) if $V\in L^q_{\mathop {\rm loc}\nolimits }(\Omega )$
 for some $q>1,$
for some $q>1,$ then $\bar u\in {\mathcal{C}}^{1,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$
then $\bar u\in {\mathcal{C}}^{1,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$ .
.
By proposition 1.3, the solutions given by theorems 1.1 and 1.2 are positive if assumption (1.1) holds with $q>\frac N2$![]() .
.
The solution we find is a bound state solution. Indeed, in § 2 we verify that no ground state solution can exist:
Proposition 1.4 Assume that $V$![]() satisfies the assumptions of theorem 1.1 or of theorem 1.2. If $V \not \equiv 0$
satisfies the assumptions of theorem 1.1 or of theorem 1.2. If $V \not \equiv 0$![]() or $\Omega \neq \mathbb {R}^N$
or $\Omega \neq \mathbb {R}^N$![]() , then problem (P) has no ground state solution.
, then problem (P) has no ground state solution.
Actually, if $V$![]() satisfies both the assumptions of theorems 1.1 and 1.2, then the solutions provided by the theorems are found exploiting the same topological configuration so it is reasonable to expect that they are the same solution. Moreover, the topological characterization suggests that they have Morse index $N$
satisfies both the assumptions of theorems 1.1 and 1.2, then the solutions provided by the theorems are found exploiting the same topological configuration so it is reasonable to expect that they are the same solution. Moreover, the topological characterization suggests that they have Morse index $N$![]() .
.
In (1.1), the assumption that $V$![]() vanishes at infinity is necessary to get the compactness condition and cannot be dropped, by the following nonexistence result (see [Reference Esteban and Lions19], [Reference Molle, Riey and Verzini34, Proposition 1.10], [Reference Cerami and Molle12, Theorem 1.1]).
vanishes at infinity is necessary to get the compactness condition and cannot be dropped, by the following nonexistence result (see [Reference Esteban and Lions19], [Reference Molle, Riey and Verzini34, Proposition 1.10], [Reference Cerami and Molle12, Theorem 1.1]).
Proposition 1.5 Let $p\in (2,2^*)$![]() , $V\in L^\infty (\mathbb {R}^N)$
, $V\in L^\infty (\mathbb {R}^N)$![]() and assume that there exists $\frac {\partial V}{\partial \nu }\in L^{\ell }(\mathbb {R}^N)$
and assume that there exists $\frac {\partial V}{\partial \nu }\in L^{\ell }(\mathbb {R}^N)$![]() for some $\nu \in \mathbb {R}^N\setminus \{0\}$
for some $\nu \in \mathbb {R}^N\setminus \{0\}$![]() and $\ell \in [\max (1,\frac {N}{2}) ,+\infty ]$
and $\ell \in [\max (1,\frac {N}{2}) ,+\infty ]$![]() , $\ell \neq 1$
, $\ell \neq 1$![]() if $N=2$
if $N=2$![]() . If $\frac {\partial V}{\partial \nu }\ge 0$
. If $\frac {\partial V}{\partial \nu }\ge 0$![]() and $\frac {\partial V}{\partial \nu }\not \equiv 0$
and $\frac {\partial V}{\partial \nu }\not \equiv 0$![]() , then problem
, then problem
has no solutions in ${\mathcal{C}}^1(\mathbb {R}^N)\cap W^{2,2}(\mathbb {R}^N)$![]() .
.
See remark 6.2 and proposition 6.3 for nonexistence results in the 1-dimensional case.
Some remarks are in order, concerning the decay assumption (D ρ) in theorem 1.1. It does not require any smallness assumption on $V$![]() and moreover does not depend on the domain, hence if it is verified then problem (P) has a solution for every exterior domain $\Omega$
and moreover does not depend on the domain, hence if it is verified then problem (P) has a solution for every exterior domain $\Omega$![]() .
.
On the other hand, (D ρ) depends on $\rho$![]() by (1.4), where $d_\rho \to \infty$
by (1.4), where $d_\rho \to \infty$![]() as $\rho \to \infty$
as $\rho \to \infty$![]() because $p<2+\frac 4N$
because $p<2+\frac 4N$![]() . As a consequence, a potential that verifies (D ρ) for every $\rho >0$
. As a consequence, a potential that verifies (D ρ) for every $\rho >0$![]() has to decay faster than any exponential.
has to decay faster than any exponential.
Remark 1.6 By the proof of theorem 1.2 we verify the existence of a constant $\bar L=\bar L(N)>0$![]() such that
such that
Instead, for $q>\frac N2$![]() ,
,
As a consequence, if $\|V\|_{N/2}$![]() is suitably small, then problem (P) in $\mathbb {R}^N$
is suitably small, then problem (P) in $\mathbb {R}^N$![]() has a solution for every $\rho >0$
has a solution for every $\rho >0$![]() , while if $V\in L^q(\mathbb {R}^N)$
, while if $V\in L^q(\mathbb {R}^N)$![]() , for $q>N/2$
, for $q>N/2$![]() , then there exists $\bar \rho =\bar \rho ({\|V\|_q})\ge 0$
, then there exists $\bar \rho =\bar \rho ({\|V\|_q})\ge 0$![]() such that problem (P) has a solution for every $\rho >\bar \rho$
such that problem (P) has a solution for every $\rho >\bar \rho$![]() (see (5.14)).
(see (5.14)).
In Theorems 1.1 and 1.2 of [Reference Molle, Riey and Verzini34] a mountain pass solution is found in the mass-supercritical case with negative potential, under smallness assumptions on $V$![]() similar to the ones considered here. In that case, if $q=N/2$
similar to the ones considered here. In that case, if $q=N/2$![]() there is a uniform bound as in (1.7) while for $q>N/2$
there is a uniform bound as in (1.7) while for $q>N/2$![]() the limits in (1.8) are reversed.
the limits in (1.8) are reversed.
If $\rho$![]() is fixed, we will observe that
is fixed, we will observe that
where
(see remark 5.1). Hence, there is no potential $V\not \equiv 0$![]() such that theorem 1.2 applies for every exterior domain $\Omega$
such that theorem 1.2 applies for every exterior domain $\Omega$![]() , for $\rho >0$
, for $\rho >0$![]() fixed.
fixed.
If we consider $V\equiv 0$![]() , then both theorems 1.1 and 1.2 apply and provide the following result.
, then both theorems 1.1 and 1.2 apply and provide the following result.
Corollary 1.7 Let $N\ge 2,$![]() $\mathbb {R}^N\setminus \Omega$
$\mathbb {R}^N\setminus \Omega$![]() compact and $\rho >0$
compact and $\rho >0$![]() , then there exist $\lambda >0$
, then there exist $\lambda >0$![]() and $\bar u\in {\mathcal{C}}^2(\Omega )$
and $\bar u\in {\mathcal{C}}^2(\Omega )$![]() , $\bar u(x)>0$
, $\bar u(x)>0$![]() , $\forall x\in \Omega$
, $\forall x\in \Omega$![]() , such that
, such that

Corollary 1.7 extends the result of [Reference Zhang and Zhang41] to the dimension 2 and to every exterior domains. The proof in [Reference Zhang and Zhang41] cannot be extended to this more general framework because it does not work in dimension 2 and when the size of $\mathbb {R}^N\setminus \Omega$![]() is large.
is large.
We prove theorems 1.1 and 1.2 by variational methods, looking for bound state solutions. The analysis of the compactness presents a lot of difficulties related to the unboundedness of the domain, that is not assumed to be symmetric. In order to recover a local compactness condition, we first see that the Lagrange multiplier $\lambda$![]() related to a Palais-Smale sequence in a negative range is positive, and then we employ a splitting Lemma from [Reference Benci and Cerami7] for PS-sequences of $E_\lambda$
related to a Palais-Smale sequence in a negative range is positive, and then we employ a splitting Lemma from [Reference Benci and Cerami7] for PS-sequences of $E_\lambda$![]() . With this decomposition in hands, we perform in proposition 3.1 a sharp fine estimate of the first energy interval $I$
. With this decomposition in hands, we perform in proposition 3.1 a sharp fine estimate of the first energy interval $I$![]() above the infimum where the compactness condition holds (see remark 3.4).
above the infimum where the compactness condition holds (see remark 3.4).
The topological argument relies on min-max techniques that make use of a barycentric map and the Brouwer degree. Since we have no smallness assumption on $\mathbb {R}^N\setminus \Omega$![]() , and in theorem 1.1 we have no bound on any Lebesgue norm of the potential, a major difficulty is to work in the compactness interval $I$
, and in theorem 1.1 we have no bound on any Lebesgue norm of the potential, a major difficulty is to work in the compactness interval $I$![]() , in the min-max procedure. To overcome this problem, we will proceed by analysing the energy interaction of positive solutions $w_1$
, in the min-max procedure. To overcome this problem, we will proceed by analysing the energy interaction of positive solutions $w_1$![]() and $w_2$
and $w_2$![]() of some suitable ‘problems at infinity’, such that $\|w_1\|_{L^2}^2+\|w_2\|_{L^2}^2=\rho ^2$
of some suitable ‘problems at infinity’, such that $\|w_1\|_{L^2}^2+\|w_2\|_{L^2}^2=\rho ^2$![]() . This idea is inspired by the unconstrained case (see [Reference Cerami and Passaseo14, Reference Lancelotti and Molle28]), where the problem at infinity is univocally determined by the choice of $\lambda$
. This idea is inspired by the unconstrained case (see [Reference Cerami and Passaseo14, Reference Lancelotti and Molle28]), where the problem at infinity is univocally determined by the choice of $\lambda$![]() . Here, the need to choose different functions $w_1,w_2$
. Here, the need to choose different functions $w_1,w_2$![]() prevents the use of the arguments developed in [Reference Cerami and Passaseo14, Reference Lancelotti and Molle28]) and requires the introduction of different and more refined estimates.
prevents the use of the arguments developed in [Reference Cerami and Passaseo14, Reference Lancelotti and Molle28]) and requires the introduction of different and more refined estimates.
To verify that the solutions we find do not change sign, we prove in proposition 2.2 that the energy of every solution that changes sign is not in the energy interval we are working in. In particular, proposition 2.2 and corollary 2.3 give information also on changing sign solutions of the autonomous problem in $\mathbb {R}^N$![]() . We point out that to get nonnegative solutions here we could exploit the symmetry of the functional and work near the cone of the positive functions, by using [Reference Ghoussoub21, Theorem 4.5] and proceeding as in [Reference Bartsch, Molle, Rizzi and Verzini6]. The advantage of this other approach is a simplification of the proof of the compactness condition, because the lack of compactness in such a case comes only from the positive solution of the problem at infinity. On the other hand, the approach we employ here allows us both to bound from below the energy of the changing sign solutions and to gain a more general analysis of the Palais-Smale sequences.
. We point out that to get nonnegative solutions here we could exploit the symmetry of the functional and work near the cone of the positive functions, by using [Reference Ghoussoub21, Theorem 4.5] and proceeding as in [Reference Bartsch, Molle, Rizzi and Verzini6]. The advantage of this other approach is a simplification of the proof of the compactness condition, because the lack of compactness in such a case comes only from the positive solution of the problem at infinity. On the other hand, the approach we employ here allows us both to bound from below the energy of the changing sign solutions and to gain a more general analysis of the Palais-Smale sequences.
The paper is organized as follows: in § 2 we introduce some preliminary results, in § 3 we prove the local compactness condition and § 4 is devoted to the sharp energy estimates that are necessary in § 5 to prove theorems 1.1 and 1.2, § 6 concerns the case $N=1$![]() and in the appendix we give a sketch of the proof of the regularity proposition, with some references for detailed proofs.
and in the appendix we give a sketch of the proof of the regularity proposition, with some references for detailed proofs.
2. Notations, variational framework and preliminary results
Throughout the paper we make use of the following notation:
• $2_c:=2+\frac 4 N$
 , ${ s}=\frac 2N\frac {p-2}{2_c-p}$
, ${ s}=\frac 2N\frac {p-2}{2_c-p}$ .
.• $L^q(\mathcal {O})$
 , $1\leq q \leq \infty$
, $1\leq q \leq \infty$ , $\mathcal {O}\subseteq \mathbb {R}^N$
, $\mathcal {O}\subseteq \mathbb {R}^N$ a measurable set, denotes the Lebesgue space, the norm in $L^q(\mathcal {O})$
a measurable set, denotes the Lebesgue space, the norm in $L^q(\mathcal {O})$ is denoted by $|\cdot |_q$
is denoted by $|\cdot |_q$ if there is no ambiguity.
if there is no ambiguity.• For $u\in H^1_0(\Omega )$
 we denote by $u$
we denote by $u$ also the function in $H^1(\mathbb {R}^N)$
also the function in $H^1(\mathbb {R}^N)$ obtained setting $u\equiv 0$
obtained setting $u\equiv 0$ in $\mathbb {R}^N\setminus \Omega$
in $\mathbb {R}^N\setminus \Omega$ .
.• For any $R>0$
 and for any $z\in \mathbb {R}^N$
and for any $z\in \mathbb {R}^N$ , $B_R(z)$
, $B_R(z)$ denotes the closed ball of radius $R$
denotes the closed ball of radius $R$ centred at $z,$
centred at $z,$ and for any measurable set $\mathcal {O} \subset \mathbb {R}^N, \ |\mathcal {O}|$
and for any measurable set $\mathcal {O} \subset \mathbb {R}^N, \ |\mathcal {O}|$ denotes its Lebesgue measure.
denotes its Lebesgue measure.• $H^{1}(\mathbb {R}^{N})$
 is the usual Sobolev space endowed with the standard norm
\[ \|u\|:=\left[\int_{\mathbb{R}^N}\left(|\nabla u|^{2}+ u^{2}\right){\rm d}\,x\right]^{\frac 12}. \]
is the usual Sobolev space endowed with the standard norm
\[ \|u\|:=\left[\int_{\mathbb{R}^N}\left(|\nabla u|^{2}+ u^{2}\right){\rm d}\,x\right]^{\frac 12}. \]
• $c,c', C, C', C_i,\ldots$
 denote various positive constants that can also vary from one line to another.
denote various positive constants that can also vary from one line to another.• $o(f)$
 and $O(f)$
and $O(f)$ denote the usual Landau notations: $\frac {o(f)}{f}\to 0$
denote the usual Landau notations: $\frac {o(f)}{f}\to 0$ as $f\to 0$
as $f\to 0$ and $|O(f)|\le C |f|$
and $|O(f)|\le C |f|$ for some positive constant $C$
for some positive constant $C$ .
.
We will find solutions $\bar u$![]() of problem $(P)$
of problem $(P)$![]() as critical points of the functional $E$
as critical points of the functional $E$![]() constrained on $S_{\rho }$
constrained on $S_{\rho }$![]() . If $\lambda$
. If $\lambda$![]() is the Lagrange multiplier related to $\bar u$
is the Lagrange multiplier related to $\bar u$![]() , then $\bar u$
, then $\bar u$![]() is also a free critical point of the related free functional $E_\lambda$
is also a free critical point of the related free functional $E_\lambda$![]() .
.
Let us assume $\lambda >0$![]() and recall some well-known properties of the limit problem, for $V\equiv 0$
and recall some well-known properties of the limit problem, for $V\equiv 0$![]() and $\Omega =\mathbb {R}^N$
and $\Omega =\mathbb {R}^N$![]() ,
,

(P ∞) has a unique positive solution $w\in H^1(\mathbb {R}^N)$![]() , up to translations, which is radial, radially decreasing, and belongs to $C^2(\mathbb {R}^N)$
, up to translations, which is radial, radially decreasing, and belongs to $C^2(\mathbb {R}^N)$![]() . The function $w$
. The function $w$![]() verifies the minimality property
verifies the minimality property
where
Correspondingly, the solutions of (P ∞) are also free critical points of the limit functional
Moreover,
and there exists $c_1>0$![]() such that
such that
Inequality $m<0$![]() in (2.2) follows choosing $u_1\in S_\rho$
in (2.2) follows choosing $u_1\in S_\rho$![]() and testing (2.1) on $u_t:=t^{N/2}u_1(t\cdot )\in S_\rho$
and testing (2.1) on $u_t:=t^{N/2}u_1(t\cdot )\in S_\rho$![]() , $t>0$
, $t>0$![]() , taking into account $p<2_c$
, taking into account $p<2_c$![]() . The positivity of $\lambda _\infty$
. The positivity of $\lambda _\infty$![]() comes from Pohozaev and Nehari identities (see also proposition 2.1). For the properties of $w$
comes from Pohozaev and Nehari identities (see also proposition 2.1). For the properties of $w$![]() we refer the reader to [Reference Bahri and Lions4, Reference Berestycki and Lions8, Reference Gidas, Ni and Nirenberg22, Reference Kwong27, Reference Strauss38].
we refer the reader to [Reference Bahri and Lions4, Reference Berestycki and Lions8, Reference Gidas, Ni and Nirenberg22, Reference Kwong27, Reference Strauss38].
For any $k>0$![]() , let us denote by $w_{k\rho ^2}$
, let us denote by $w_{k\rho ^2}$![]() the positive solution of
the positive solution of

where $w_{k\rho ^2}$![]() verifies
verifies
It turns out that
where
(see notations). From $p<2_c$![]() it follows $s>0$
it follows $s>0$![]() . By (2.7), in particular we have:
. By (2.7), in particular we have:
For $k=0$![]() we set $w_0=0$
we set $w_0=0$![]() and for $k=1$
and for $k=1$![]() we simply write $w_{\rho ^2}=w$
we simply write $w_{\rho ^2}=w$![]() .
.
Moreover, for any $k>0$![]() , by (2.3), (2.4) and (2.7) we have
, by (2.3), (2.4) and (2.7) we have
where
From $p<2_c$![]() there follows $\frac {1}{p-2}-\frac {N-1}{4}>0$
there follows $\frac {1}{p-2}-\frac {N-1}{4}>0$![]() , so that
, so that
Proof Proof of proposition 1.4
Let us prove that
and the infimum is not achieved.
Obviously we have that ${\inf _{S_{\rho }} E\geq m}$![]() . To show that the equality holds, let us consider the sequence $(u_n)_n$
. To show that the equality holds, let us consider the sequence $(u_n)_n$![]() defined by $u_n=w(x-y_n)$
defined by $u_n=w(x-y_n)$![]() , where $(y_n)_n$
, where $(y_n)_n$![]() is a sequence in $\mathbb {R}^N$
is a sequence in $\mathbb {R}^N$![]() such that $|y_n|\to +\infty$
such that $|y_n|\to +\infty$![]() . By (1.1) and (2.3), and taking into account (D ρ) or (1.5), we have that
. By (1.1) and (2.3), and taking into account (D ρ) or (1.5), we have that
which implies $\displaystyle {\lim _{n\to +\infty } E(u_n)=m}$![]() .
.
Now, assume by contradiction that the infimum ${\inf _{S_{\rho }} E}$![]() is achieved by a function $\bar u$
is achieved by a function $\bar u$![]() . Then, by
. Then, by
and by the uniqueness of the minimizers of (2.1), we should have $\bar {u}=\pm w(x-\bar {y})$![]() for a suitable $\bar y\in \mathbb {R}^N$
for a suitable $\bar y\in \mathbb {R}^N$![]() . Since $w(x-\bar {y})>0$
. Since $w(x-\bar {y})>0$![]() for all $x\in \mathbb {R}^N$
for all $x\in \mathbb {R}^N$![]() , we can deduce that $\Omega$
, we can deduce that $\Omega$![]() must be the entire space $\mathbb {R}^N$
must be the entire space $\mathbb {R}^N$![]() and by (2.12) we get:
and by (2.12) we get:
that implies $V \equiv 0$![]() because $V\ge 0$
because $V\ge 0$![]() . So we are in contradiction with $\Omega \neq \mathbb {R}^N$
. So we are in contradiction with $\Omega \neq \mathbb {R}^N$![]() or $V\not \equiv 0$
or $V\not \equiv 0$![]() .
.
Next proposition states the positivity of the Lagrange multipliers in (P).
Proposition 2.1 Assume that $u\in S_\rho$![]() and $\lambda \in \mathbb {R}$
and $\lambda \in \mathbb {R}$![]() solve (P). If $E(u)<0$
solve (P). If $E(u)<0$![]() , then $\lambda >0$
, then $\lambda >0$![]() .
.
Proof We have
Then,

Before concluding this section, let us find out some features of the changing sign solutions.
Proposition 2.2 Let $u\in S_\rho$![]() be a solution of (P) ($(P_\infty )$
be a solution of (P) ($(P_\infty )$![]() ). If $u$
). If $u$![]() changes sign, then $E(u) > 2^{-s}m$
changes sign, then $E(u) > 2^{-s}m$![]() ($E_\infty (u) > 2^{-s}m$
($E_\infty (u) > 2^{-s}m$![]() ).
).
Proof Since $m<0$![]() , we can assume $E(u)<0$
, we can assume $E(u)<0$![]() . According to proposition 2.1, let $\lambda >0$
. According to proposition 2.1, let $\lambda >0$![]() be the Lagrange multiplier corresponding to the solution $u$
be the Lagrange multiplier corresponding to the solution $u$![]() and let $w_\infty \in H^1(\mathbb {R}^N)$
and let $w_\infty \in H^1(\mathbb {R}^N)$![]() be the positive solution of $-\Delta v+\lambda v=v^{p-1}$
be the positive solution of $-\Delta v+\lambda v=v^{p-1}$![]() . By (2.7),
. By (2.7),

Let us write $u=u^+-u^-$![]() , where $u^\pm =\max \{\pm u,0\}$
, where $u^\pm =\max \{\pm u,0\}$![]() , $\rho ^2=|u^+|_2^2+|u^-|_2^2$
, $\rho ^2=|u^+|_2^2+|u^-|_2^2$![]() . Since $u^+$
. Since $u^+$![]() and $u^-$
and $u^-$![]() are on the Nehari manifold ${\mathcal {N}}$
are on the Nehari manifold ${\mathcal {N}}$![]() corresponding to $E_\lambda$
corresponding to $E_\lambda$![]() , then $(E_\lambda )_{|_{\mathcal {N}}}(u^\pm ) > E_{\lambda,\infty }(w_\infty )$
, then $(E_\lambda )_{|_{\mathcal {N}}}(u^\pm ) > E_{\lambda,\infty }(w_\infty )$![]() (see [Reference Benci and Cerami7] and [Reference Molle, Musso and Passaseo31, Proposition 2.1]). Namely, by (2.14),
(see [Reference Benci and Cerami7] and [Reference Molle, Musso and Passaseo31, Proposition 2.1]). Namely, by (2.14),

Hence, the claim read as

and, equivalently, as

Since $(\lambda,w_\infty )$![]() solves (2.5) for $k=\frac {|w_\infty |^2_2}{\rho ^2}$
solves (2.5) for $k=\frac {|w_\infty |^2_2}{\rho ^2}$![]() , the following system is fulfilled
, the following system is fulfilled

Solving (2.16) and taking into account (2.7) we get
Putting (2.17) in (2.15), we have to verify

Then the assertion is proved because $\frac {2p-N(p-2)}{4-N(p-2)}=1+s$![]() and
and
Corollary 2.3 If $u$![]() is a changing sign solution of
is a changing sign solution of
then $|u|_2^2> 2|w_\infty |_2^2$![]() , where $w_\infty$
, where $w_\infty$![]() denotes the positive solution of (2.18).
denotes the positive solution of (2.18).
Clearly, here $\lambda >0$![]() by Pohozaev identity.
by Pohozaev identity.
Proof Let us call $E(u)=M$![]() . From system (2.16) applied to $u$
. From system (2.16) applied to $u$![]() and $w_\infty$
and $w_\infty$![]() it follows
it follows
By proposition 2.2, $M>2^{-s}m_{|u|_2^2}$![]() , then, by (2.7) and (2.19),
, then, by (2.7) and (2.19),

that completes the proof.
3. The compactness condition
Proposition 3.1 Let $(u_n)_n$![]() be a Palais-Smale sequence at the level $c$
be a Palais-Smale sequence at the level $c$![]() for $E$
for $E$![]() constrained on $S_\rho$
constrained on $S_\rho$![]() . If $c\in (m,2^{-s}m)$
. If $c\in (m,2^{-s}m)$![]() then there exists a critical point $u_0\in S_\rho$
then there exists a critical point $u_0\in S_\rho$![]() such that $u_n\to u_0$
such that $u_n\to u_0$![]() , as $n\to \infty$
, as $n\to \infty$![]() .
.
To prove proposition 3.1, we will use the well known splitting lemma of Benci and Cerami for the unconstrained problem ([Reference Benci and Cerami7, Lemma 3.1]).
Lemma 3.2 Let $\lambda >0$![]() and let $(u_n)_n$
and let $(u_n)_n$![]() in $H^1(\mathbb {R}^N)$
in $H^1(\mathbb {R}^N)$![]() be a Palais-Smale sequence for $E_\lambda$
be a Palais-Smale sequence for $E_\lambda$![]() . Then there exist a critical point $u_0$
. Then there exist a critical point $u_0$![]() of $E_\lambda$
of $E_\lambda$![]() , an integer $h\ge 0$
, an integer $h\ge 0$![]() , $h$
, $h$![]() non-trivial solutions $w^1,\dots,w^h\in H^1(\mathbb {R}^N)$
non-trivial solutions $w^1,\dots,w^h\in H^1(\mathbb {R}^N)$![]() to the limit equation
to the limit equation
and $h$![]() sequences $(y_n^j)_n\subset \mathbb {R}^N$
sequences $(y_n^j)_n\subset \mathbb {R}^N$![]() , $1\le j\le h$
, $1\le j\le h$![]() , such that $|y_n^j|\to \infty$
, such that $|y_n^j|\to \infty$![]() as $n\to \infty$
as $n\to \infty$![]() , and
, and

up to a subsequence. Moreover, we have:

and

Proof Proof of proposition 3.1
We claim that $(u_n)_n$![]() is bounded in $H^1_0(\Omega )$
is bounded in $H^1_0(\Omega )$![]() . Indeed, $u_n\in S_\rho$
. Indeed, $u_n\in S_\rho$![]() , $\forall n\in \mathbb {N}$
, $\forall n\in \mathbb {N}$![]() , and by the Gagliardo-Nirenberg inequality
, and by the Gagliardo-Nirenberg inequality
(see [Reference Leoni29, Theorem 12.83]) we have:
with $\frac {N(p-2)}{2}<2$![]() because $p<2_c$
because $p<2_c$![]() .
.
Since $(u_n)_n$![]() is a constrained PS-sequence, there exists a sequence $(\lambda _n)_n$
is a constrained PS-sequence, there exists a sequence $(\lambda _n)_n$![]() in $\mathbb {R}$
in $\mathbb {R}$![]() such that
such that

Setting $v=u_n$![]() in (3.6), and taking into account that $(u_n)_n$
in (3.6), and taking into account that $(u_n)_n$![]() is bounded in $H^1$
is bounded in $H^1$![]() , we can argue as in (2.13) obtaining
, we can argue as in (2.13) obtaining
for large $n$![]() . Since $(u_n)_n$
. Since $(u_n)_n$![]() is bounded in $H^1_0(\Omega )$
is bounded in $H^1_0(\Omega )$![]() , the first relation in (3.7) implies that the sequence $(\lambda _n)_n$
, the first relation in (3.7) implies that the sequence $(\lambda _n)_n$![]() is bounded. Moreover, from (3.7) we infer also that $\lambda _n\ge c>0$
is bounded. Moreover, from (3.7) we infer also that $\lambda _n\ge c>0$![]() , for a suitable constant $c$
, for a suitable constant $c$![]() . Then we can assume that $\lambda _n\to \lambda >0$
. Then we can assume that $\lambda _n\to \lambda >0$![]() . Hence, by (3.6) we are in position to apply lemma 3.2 and we can decompose $u_n$
. Hence, by (3.6) we are in position to apply lemma 3.2 and we can decompose $u_n$![]() according to (3.1).
according to (3.1).
$(I)$![]() If $h=0$
If $h=0$![]() , we are done.
, we are done.
So, we assume by contradiction $h\ge 1$![]() and we are going to show that then
and we are going to show that then

up to the case $u_0=0$![]() , $h=1$
, $h=1$![]() and $w^1>0$
and $w^1>0$![]() , that arises for
, that arises for
Once (3.8) is proved, the contradiction comes out, because (3.2) and (3.3) provide $c=E (u_0)+\sum _{j=1}^h E_{\infty }(w^j)$![]() , and $c\in (m,2^{-s}m)$
, and $c\in (m,2^{-s}m)$![]() by assumption.
by assumption.
$(II)$![]() If $u_0\equiv 0$
If $u_0\equiv 0$![]() and $h=1$
and $h=1$![]() occurs, then $|w^1|_2=\rho$
occurs, then $|w^1|_2=\rho$![]() , by (3.3). Hence, if $w^1>0$
, by (3.3). Hence, if $w^1>0$![]() then $c=m$
then $c=m$![]() by (3.2) and (2.1), so (3.9) is proved. We observe that this is the only case in which (3.9) holds, up to the autonomous case $\Omega =\mathbb {R}^N$
by (3.2) and (2.1), so (3.9) is proved. We observe that this is the only case in which (3.9) holds, up to the autonomous case $\Omega =\mathbb {R}^N$![]() and $V\equiv 0$
and $V\equiv 0$![]() , when also the case $u_0>0$
, when also the case $u_0>0$![]() and $h=1$
and $h=1$![]() verifies (3.9). On the other hand, if $w^1$
verifies (3.9). On the other hand, if $w^1$![]() is a changing sign solution, then $c>2^{-s} m$
is a changing sign solution, then $c>2^{-s} m$![]() by proposition 2.2.
by proposition 2.2.
$(III)$![]() If $u_0\equiv 0$
If $u_0\equiv 0$![]() and $h\ge 2$
and $h\ge 2$![]() , we proceed by induction. For $h=2$
, we proceed by induction. For $h=2$![]() , we get (3.8) arguing exactly as in the proof of proposition 2.2, with $w^1$
, we get (3.8) arguing exactly as in the proof of proposition 2.2, with $w^1$![]() in place of $u^+$
in place of $u^+$![]() and $w^2$
and $w^2$![]() in place of $u^-$
in place of $u^-$![]() . Observe that the case $w^1=w^2>0$
. Observe that the case $w^1=w^2>0$![]() is the only case when the equality holds in (3.8).
is the only case when the equality holds in (3.8).
Suppose now $h\ge 3$![]() and (3.8) holds for $h-1$
and (3.8) holds for $h-1$![]() , namely for every $\rho _1>0$
, namely for every $\rho _1>0$![]()

whenever $w^j\not \equiv 0$![]() , for all $j\in \{1,\ldots,h-1\}$
, for all $j\in \{1,\ldots,h-1\}$![]() , and $\sum _{j=1}^{h-1}|w^j|_2^2=\rho _1^2$
, and $\sum _{j=1}^{h-1}|w^j|_2^2=\rho _1^2$![]() . Then, let us prove (3.8) for $h$
. Then, let us prove (3.8) for $h$![]() . We can assume that $|w^h|_2^2\le \rho ^2/3$
. We can assume that $|w^h|_2^2\le \rho ^2/3$![]() . Taking into account (3.10) and (2.7), we have:
. Taking into account (3.10) and (2.7), we have:

Hence, it is sufficient to verify that

Inequality (3.11) is equivalent to
where $t:=\frac {|w^h|_2^2}{\rho ^2}\in (0,1/3]$![]() . Since inequality (3.12) holds for every $t\in [0,1/3]$
. Since inequality (3.12) holds for every $t\in [0,1/3]$![]() , estimate (3.8) is proved for $u_0\equiv 0$
, estimate (3.8) is proved for $u_0\equiv 0$![]() .
.
$(IV)$![]() If $u_0\not \equiv 0$
If $u_0\not \equiv 0$![]() , we can proceed as in the previous steps: first by considering the case $h=1$
, we can proceed as in the previous steps: first by considering the case $h=1$![]() and arguing as in the proof of proposition 2.2, and then finishing the proof by induction.
and arguing as in the proof of proposition 2.2, and then finishing the proof by induction.
Corollary 3.3 If $(u_n)_n$![]() in $S_\rho$
in $S_\rho$![]() satisfies $\lim \limits _{n\to \infty }E(u_n)=m$
satisfies $\lim \limits _{n\to \infty }E(u_n)=m$![]() , then there exists a sequence $(y_n)_n$
, then there exists a sequence $(y_n)_n$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() such that
such that
If $\Omega \neq \mathbb {R}^N$![]() or $V\not \equiv 0$
or $V\not \equiv 0$![]() , then $|y_n|\mathop {\longrightarrow }\infty$
, then $|y_n|\mathop {\longrightarrow }\infty$![]() , as $n\to \infty$
, as $n\to \infty$![]() .
.
Proof By the Ekeland variational principle, there exists a PS-sequence $(v_n)_n$![]() for $E$
for $E$![]() constrained on $S_\rho$
constrained on $S_\rho$![]() such that $\lim \limits _{n\to \infty }E(v_n)=m$
such that $\lim \limits _{n\to \infty }E(v_n)=m$![]() and $u_n=v_n+o(1)$
and $u_n=v_n+o(1)$![]() in $H^1$
in $H^1$![]() (see ([Reference Ekeland18, Proposition 5.1]), then we can assume that $(u_n)_n$
(see ([Reference Ekeland18, Proposition 5.1]), then we can assume that $(u_n)_n$![]() is PS-sequence. Then (3.13) is a direct consequence of (3.9) and part $(II)$
is PS-sequence. Then (3.13) is a direct consequence of (3.9) and part $(II)$![]() in the proof of proposition 3.1.
in the proof of proposition 3.1.
If $y_n\to \bar y\in \mathbb {R}^N$![]() , up to a subsequence, then $u_n\to w(\cdot -\bar y)$
, up to a subsequence, then $u_n\to w(\cdot -\bar y)$![]() in $H^1$
in $H^1$![]() and a.e., so that $\Omega =\mathbb {R}^N$
and a.e., so that $\Omega =\mathbb {R}^N$![]() because $w(x)>0$
because $w(x)>0$![]() , $\forall x \in \mathbb {R}^N$
, $\forall x \in \mathbb {R}^N$![]() . Moreover
. Moreover

implies $V\equiv 0$![]() , again because $w(x)>0$
, again because $w(x)>0$![]() , $\forall x\in \mathbb {R}^N$
, $\forall x\in \mathbb {R}^N$![]() .
.
So the proof is completed.
Remark 3.4 By $(III)$![]() in the proof of proposition 3.1 we see that, for every sequence $(y_n)_n$
in the proof of proposition 3.1 we see that, for every sequence $(y_n)_n$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() such that $\lim _{n\to \infty }|y_n|=\infty$
such that $\lim _{n\to \infty }|y_n|=\infty$![]() ,
,
Then the sequence $(w_{{\rho ^2}/{2}}(\cdot -y_n)+w_{{\rho ^2}/{2}}(\cdot +y_n))_n$![]() turns out to be a not relatively compact PS-sequence at the level $2^{-s}m$
turns out to be a not relatively compact PS-sequence at the level $2^{-s}m$![]() , showing that the compactness interval $(m,2^{-s}m)$
, showing that the compactness interval $(m,2^{-s}m)$![]() cannot be extended.
cannot be extended.
4. Energy estimates
4.1 An upper bound
If $\mathbb {R}^N\setminus \Omega$![]() is a non empty compact set contained in $B_{R-1}(0)$
is a non empty compact set contained in $B_{R-1}(0)$![]() , let us introduce the cut-off function $\vartheta$
, let us introduce the cut-off function $\vartheta$![]() , verifying
, verifying
If $\Omega =\mathbb {R}^N$![]() , we agree that $\vartheta \equiv 1$
, we agree that $\vartheta \equiv 1$![]() on $\mathbb {R}^N$
on $\mathbb {R}^N$![]() . Let us set $\Sigma =\partial B_2(e_1)$
. Let us set $\Sigma =\partial B_2(e_1)$![]() , where $e_1$
, where $e_1$![]() is the first element of the canonical basis of $\mathbb {R}^N$
is the first element of the canonical basis of $\mathbb {R}^N$![]() , and for any $r>0$
, and for any $r>0$![]() define the map $\psi _r: [0,1]\times \Sigma \longrightarrow H^1_0(\Omega )$
define the map $\psi _r: [0,1]\times \Sigma \longrightarrow H^1_0(\Omega )$![]() by
by

Proposition 4.1 Suppose that $V$![]() verifies (1.1) and (D ρ), then
verifies (1.1) and (D ρ), then
(a) there exist $\overline {r}>0$
 such that for any $r>\overline {r}$
such that for any $r>\overline {r}$ (4.3)\begin{equation} {\mathcal{A}}_r=\max\left\{E\left(\psi_{r}[t,z]\right):\quad t\in [0,1],\, z\in\Sigma\right\} <2^{-{ s}}\,m; \end{equation}
(4.3)\begin{equation} {\mathcal{A}}_r=\max\left\{E\left(\psi_{r}[t,z]\right):\quad t\in [0,1],\, z\in\Sigma\right\} <2^{-{ s}}\,m; \end{equation}
(b) for every $\varepsilon >0$
 there exists $r_\varepsilon >0$
there exists $r_\varepsilon >0$ such that for any $r>r_\varepsilon$
such that for any $r>r_\varepsilon$ (4.4)\begin{equation} {\mathcal{L}}_r=\max\left\{E\left(\psi_{r}[1,z]\right)\ :\ z\in\Sigma\right\} \leq m+\varepsilon. \end{equation}
(4.4)\begin{equation} {\mathcal{L}}_r=\max\left\{E\left(\psi_{r}[1,z]\right)\ :\ z\in\Sigma\right\} \leq m+\varepsilon. \end{equation}
Remark 4.2 In proposition 4.1, $V\equiv 0$![]() is allowed.
is allowed.
Before proving proposition 4.1, let us recall two technical lemmas. For the proof of Lemma 4.3 we refer to [Reference Cerami and Passaseo14] while the proof of Lemma 4.4 is in [Reference Bahri and Li3] (see also Lemma 2.9 in [Reference Cerami and Molle13]).
Lemma 4.3 For all $a,b\ge 0$![]() , for all $p\ge 2$
, for all $p\ge 2$![]() , the following relation holds true
, the following relation holds true
Lemma 4.4 If $g \in L^\infty (\mathbb {R}^N)$![]() and $h\in L^1(\mathbb {R}^N)$
and $h\in L^1(\mathbb {R}^N)$![]() are such that, for some $\alpha \ge 0$
are such that, for some $\alpha \ge 0$![]() , $b\ge 0$
, $b\ge 0$![]() , $\gamma \in \mathbb {R}$
, $\gamma \in \mathbb {R}$![]()
and
then, for every $z\in \mathbb {R}^N\setminus \{0\}$![]() ,
,
Lemma 4.5 Let $z\in \Sigma$![]() . For every $t\in [0,1/2]$
. For every $t\in [0,1/2]$![]() and $r>0$
and $r>0$![]() , let us set
, let us set
Then the following facts hold:
(1) if $t\in [0,\frac 12 )$
 , then $\displaystyle \frac {\tau _t(r)}{\delta _t(r)}\to c_{1,t}:= c_t\int _{\mathbb {R}^N} w_{(1-t)\rho ^2}(y)\, e^{-\sqrt {t^s\lambda _{\infty }}\,\frac {y\cdot (e_1-z)}{2}}\,{\rm d}y, \mbox {as }r\to \infty$
, then $\displaystyle \frac {\tau _t(r)}{\delta _t(r)}\to c_{1,t}:= c_t\int _{\mathbb {R}^N} w_{(1-t)\rho ^2}(y)\, e^{-\sqrt {t^s\lambda _{\infty }}\,\frac {y\cdot (e_1-z)}{2}}\,{\rm d}y, \mbox {as }r\to \infty$ ,
,(2) if $t\in [0,\frac 12 ]$
 , then $\displaystyle \frac {\sigma _t(r)}{\delta _t(r)}\to c_{2,t}:=2 c_t\int _{\mathbb {R}^N} w^{p-1}_{(1-t)\rho ^2}(y)\, e^{-\sqrt {t^s\lambda _{\infty }}\,\frac {y\cdot (e_1-z)}{2}}\,{\rm d}y, \mbox {as }r\to \infty$
, then $\displaystyle \frac {\sigma _t(r)}{\delta _t(r)}\to c_{2,t}:=2 c_t\int _{\mathbb {R}^N} w^{p-1}_{(1-t)\rho ^2}(y)\, e^{-\sqrt {t^s\lambda _{\infty }}\,\frac {y\cdot (e_1-z)}{2}}\,{\rm d}y, \mbox {as }r\to \infty$ where $c_t=c_1 t^{{ s}}(\frac {1}{p-2}-\frac {N-1}{4})$
where $c_t=c_1 t^{{ s}}(\frac {1}{p-2}-\frac {N-1}{4})$ (see (2.3)). Moreover,
(see (2.3)). Moreover,(3) $c_{1,t}\cdot (\frac {1}{2}-t) \leq C$
 for every $t\in [0,\frac 12)$
for every $t\in [0,\frac 12)$ .
.
Remark 4.6 The definition of $\tau _t(r),\sigma _t(r)$![]() is independent of $z$
is independent of $z$![]() , by symmetry. Moreover, $c_{1,t}\to \infty$
, by symmetry. Moreover, $c_{1,t}\to \infty$![]() as $t\to \frac 12$
as $t\to \frac 12$![]() and, clearly, $\tau _0(r)=\sigma _0(r)\equiv 0$
and, clearly, $\tau _0(r)=\sigma _0(r)\equiv 0$![]() .
.
Proof Assertions $(1),(2)$![]() easily follow using (2.9) and by lemma 4.4. Let us prove assertion $3)$
easily follow using (2.9) and by lemma 4.4. Let us prove assertion $3)$![]() .
.
Without loss of generality we may assume $z=-e_1$![]() , so that $\frac {z-e_1}{2}=-e_1$
, so that $\frac {z-e_1}{2}=-e_1$![]() , and to simplify the notations we consider $\lambda _\infty =1$
, and to simplify the notations we consider $\lambda _\infty =1$![]() . Moreover, since $t\mapsto c_{1,t}$
. Moreover, since $t\mapsto c_{1,t}$![]() is a continuous function on $[0,1/2]$
is a continuous function on $[0,1/2]$![]() , it is sufficient to prove
, it is sufficient to prove
where $y_1$![]() is the first component of $y\in \mathbb {R}^N$
is the first component of $y\in \mathbb {R}^N$![]() . Moreover, by (2.9) we are left to prove that
. Moreover, by (2.9) we are left to prove that

If we set $a=\frac {1}{2}-t$![]() , then $a\to 0^+$
, then $a\to 0^+$![]() as $t\to (1/2)^-$
as $t\to (1/2)^-$![]() , and since $[(1-t)^{s/2}-t^{s/2}]\ge ca$
, and since $[(1-t)^{s/2}-t^{s/2}]\ge ca$![]() as $a\to 0$
as $a\to 0$![]() , with $c>0$
, with $c>0$![]() , (4.10) can be estimated by
, (4.10) can be estimated by

Making use of spherical coordinates in the subspace $e_1^{\perp }=\left \{v\in \mathbb {R}^N\ :\ v\cdot e_1=0\right \}$![]() , denoting by $b=(\frac 14)^{s/2}$
, denoting by $b=(\frac 14)^{s/2}$![]() and $\mathbb {R}^2_+=\mathbb {R}\times [0,+\infty )$
and $\mathbb {R}^2_+=\mathbb {R}\times [0,+\infty )$![]() , we have to analyse
, we have to analyse

Setting $k=ca+b(1-\cos {\vartheta })$![]() , we can estimate
, we can estimate

Then,

Since $1-\cos {\vartheta }\ge \frac {1}{4}\sin ^2{\vartheta }$![]() for small $\vartheta$
for small $\vartheta$![]() , if we set $u=\sin {\vartheta }$
, if we set $u=\sin {\vartheta }$![]() and $\beta =b/(4c)$
and $\beta =b/(4c)$![]() , then it is sufficient to evaluate
, then it is sufficient to evaluate

and the assertion follows.
Proof Proof of proposition 4.1
In this proof we shall consider $R>1$![]() fixed such that $\mathbb {R}^N\setminus \Omega \subset B_{R-1}(0)$
fixed such that $\mathbb {R}^N\setminus \Omega \subset B_{R-1}(0)$![]() .
.
In order to simplify the notations, we often omit $t,z$![]() and write $\psi _r=\psi _r[t,z]$
and write $\psi _r=\psi _r[t,z]$![]() , $\delta (r)=\delta _t(r)$
, $\delta (r)=\delta _t(r)$![]() , $\sigma (r)=\sigma _t(r)$
, $\sigma (r)=\sigma _t(r)$![]() , $\tau (r)=\tau _t(r)$
, $\tau (r)=\tau _t(r)$![]() (see (4.2), (4.7), (4.8), (4.9)).
(see (4.2), (4.7), (4.8), (4.9)).
We have that
So, to get the statement of the proposition, we need to estimate these two integrals.
Let us consider $0\leq t\leq 1/2$![]() . In an entirely analogous way we may treat also the case $1/2< t\leq 1$
. In an entirely analogous way we may treat also the case $1/2< t\leq 1$![]() .
.
Let us set:
and for any $i=1,2$![]()
Recall that
namely

and so
Evidently for $t=\frac {1}{2}$![]() we have $w_1=w_2$
we have $w_1=w_2$![]() , $\lambda _1=\lambda _2$
, $\lambda _1=\lambda _2$![]() , $A_1=A_2$
, $A_1=A_2$![]() , $B_1=B_2$
, $B_1=B_2$![]() . Moreover, we recall that
. Moreover, we recall that
With these notations,
Estimate of $\displaystyle {\left |\vartheta (\cdot )[w_1(\cdot -r z)+w_2(\cdot -r e_1)]\right |_2}$![]() .
.
From above

From below,

By the asymptotic behaviour of $w_1$![]() and $w_2$
and $w_2$![]() (see (2.9)), for any $q\geq 2$
(see (2.9)), for any $q\geq 2$![]() we have
we have

Therefore, by (4.14), (4.15) and (4.16) we get
Estimate of $\displaystyle {\int _{\mathbb {R}^N} [|\nabla \psi _r|^2+V(x)\psi _r^2]\,{\rm d}\,x}$![]() .
.
Now, let us estimate

By direct computation, (4.11) and (4.12), we obtain

Since $\nabla \vartheta \equiv 0$![]() on $\mathbb {R}^N\setminus B_R(0)$
on $\mathbb {R}^N\setminus B_R(0)$![]() , by using (2.9) (2.10) we get
, by using (2.9) (2.10) we get

and

According to the contribution of the potential, by (D ρ), (2.9) and by lemma 4.4 we have


Estimate of $\int _{\mathbb {R}^N}|\psi _r|^p{\rm d}\,x$![]() .
.
Since $0\le \vartheta (x)\le 1$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() and $\vartheta \equiv 1$
and $\vartheta \equiv 1$![]() in $\mathbb {R}^N\setminus B_{R}(0)$
in $\mathbb {R}^N\setminus B_{R}(0)$![]() , by (4.16) and by lemma 4.3, we get
, by (4.16) and by lemma 4.3, we get

Taking into account (4.14) and (4.24) we have that

Estimate of $E(\psi _r)$![]() .
.
Therefore

Observe that for every $\sigma,\tau >0$![]() and $\delta \to 0$
and $\delta \to 0$![]() we have
we have

where

and we have performed a Taylor expansion with respect to $o(\delta )$![]() . We will write $\varphi _t$
. We will write $\varphi _t$![]() in place of $\varphi$
in place of $\varphi$![]() when we want to emphasize the role of $t$
when we want to emphasize the role of $t$![]() .
.
Now, we are going to consider the Taylor expansion of $\varphi$![]() . Observe that these expansions are consistent by (1) and (2) in lemma 4.5.
. Observe that these expansions are consistent by (1) and (2) in lemma 4.5.
By (4.13), and taking into account (4.12), we have that

Hence, we obtain

Now, we want to analyse the asymptotic behaviour of $\varphi (\tau (r),\sigma (r))$![]() and, as a consequence, of $E(\psi _r)$
and, as a consequence, of $E(\psi _r)$![]() , as $r\to \infty$
, as $r\to \infty$![]() .
.
By lemma 4.5, for every $t\in [0,\frac 12)$![]() we have
we have

Taking into account lemma 4.5 and $\lambda _1\to \lambda _2$![]() as $t\to \frac 12$
as $t\to \frac 12$![]() , we get
, we get

Then, for suitable constants $C>0$![]() and $\mu \in ( 0,\frac 12)$
and $\mu \in ( 0,\frac 12)$![]()
(see (4.26). Since $\delta _t(r)\to 0$![]() as $r\to \infty$
as $r\to \infty$![]() , uniformly in $t$
, uniformly in $t$![]() (see (4.7)), we can conclude that there exists $r_1>0$
(see (4.7)), we can conclude that there exists $r_1>0$![]() such that
such that
If $t=\frac 12$![]() , for suitable $\alpha,\beta,\gamma \in \mathbb {R}$
, for suitable $\alpha,\beta,\gamma \in \mathbb {R}$![]() we infer
we infer

Now, consider that by lemma 4.5
and that, fixed $\eta \in (0,\sqrt {2^{-{ s}}\lambda _{\infty }}/2]$![]() , by lemma 4.4
, by lemma 4.4
so that
By (4.30), (4.31), (4.32), we can conclude that there exists $r_2>0$![]() such that
such that
If $t\in [0,\mu ]$![]() , then, taking into account that $\delta _t(r)\le \delta _0(r)$
, then, taking into account that $\delta _t(r)\le \delta _0(r)$![]() for every $t\in [0,1/2]$
for every $t\in [0,1/2]$![]() , we get
, we get

Since $[\mu ^{1+s}+(1-\mu )^{1+s}]m<2^{-s}m$![]() , there exists $r_3>0$
, there exists $r_3>0$![]() such that
such that
So, assertion $(a)$![]() follows from (4.29), (4.33), (4.34), for every $r>\bar r:=\max \{r_1,r_2,r_3\}$
follows from (4.29), (4.33), (4.34), for every $r>\bar r:=\max \{r_1,r_2,r_3\}$![]() .
.
The estimates developed above also show that
so that $E(\psi _r[0,z])\mathop {\longrightarrow } m$![]() , as $r\to \infty$
, as $r\to \infty$![]() . The same arguments work to evaluate
. The same arguments work to evaluate
uniformly in $z\in \Sigma$![]() . So, also $(b)$
. So, also $(b)$![]() is proved.
is proved.
4.2 Other estimates
In this subsection we consider the nonautonomous case $\Omega \neq \mathbb {R}^N$![]() or $V\not \equiv 0$
or $V\not \equiv 0$![]() .
.
The following definition of barycentre of a function $u \in H^1(\mathbb {R}^N)\setminus \left \lbrace 0 \right \rbrace,$![]() has been introduced in [Reference Cerami and Passaseo15]. We set
has been introduced in [Reference Cerami and Passaseo15]. We set
and we remark that $\mu (u)$![]() is bounded and continuous, so we can introduce the function
is bounded and continuous, so we can introduce the function
that is continuous and has compact support. Thus, we can set $\beta : H^1(\mathbb {R}^N)\setminus \{0\}\rightarrow \mathbb {R}^N$![]() as
as
The map $\beta$![]() has the following properties:
has the following properties:
Let us set
Lemma 4.7 We have that $C_0>m$![]() .
.
Proof Of course we have that $C_0\geq m$![]() . Assume by contradiction that $C_0=m$
. Assume by contradiction that $C_0=m$![]() . Then by corollary 3.3 there exists a sequence $(y_n)_n$
. Then by corollary 3.3 there exists a sequence $(y_n)_n$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() such that $|y_n|\mathop {\longrightarrow } \infty$
such that $|y_n|\mathop {\longrightarrow } \infty$![]() , as $n\to \infty$
, as $n\to \infty$![]() , and
, and
By (4.37), (4.38) and (4.40) we have
contrary to $|y_n|\mathop {\longrightarrow } \infty$![]() , as $n\to \infty$
, as $n\to \infty$![]() .
.
So the proof is completed
Lemma 4.8 Let ${\mathcal {A}}_r$![]() and ${\mathcal {L}}_r$
and ${\mathcal {L}}_r$![]() be as in proposition 4.1. Then $\widehat {r}>0$
be as in proposition 4.1. Then $\widehat {r}>0$![]() exists such that
exists such that
Proof Inequality ${\mathcal {L}}_r< C_0$![]() , for large $r$
, for large $r$![]() , follows from (4.4) and lemma 4.7.
, follows from (4.4) and lemma 4.7.
To get the second inequality in (4.40), we claim that $\beta (\vartheta (\cdot )w(\cdot -rz))\cdot z >0$![]() for all $z\in \Sigma$
for all $z\in \Sigma$![]() , for large $r$
, for large $r$![]() . Indeed, by (4.36),(4.37) and (4.39) we have
. Indeed, by (4.36),(4.37) and (4.39) we have
because $\vartheta (\cdot +rz)w\to w$![]() in $H^1$
in $H^1$![]() as $r\to \infty$
as $r\to \infty$![]() , by (2.3) and (2.4). Hence
, by (2.3) and (2.4). Hence
as asserted. So, for $r$![]() large, the deformation ${\mathcal {G}}:[0,1]\times \Sigma \to \mathbb {R}^N\setminus \{0\}$
large, the deformation ${\mathcal {G}}:[0,1]\times \Sigma \to \mathbb {R}^N\setminus \{0\}$![]() given by
given by
is well defined. Then we claim that there exists $(t_r,z_r)\in [0,1]\times \Sigma$![]() such that
such that
Indeed, by the continuity of the maps $\beta$![]() and $\psi _r$
and $\psi _r$![]() , by ${\mathcal {G}}(s,z)\neq 0$
, by ${\mathcal {G}}(s,z)\neq 0$![]() , $\forall (s,z)\in [0,1]\times \Sigma$
, $\forall (s,z)\in [0,1]\times \Sigma$![]() , and by the invariance of the topological degree by homotopy, we have
, and by the invariance of the topological degree by homotopy, we have
From (4.43) there follows $C_0\leq E(\psi _r[t_r,z_r])\leq {\mathcal {A}}_r$![]() , that completes the proof.
, that completes the proof.
5. Proof of the main results
The existence of a positive solution for the autonomous case $\Omega =\mathbb {R}^N$![]() and $V\equiv 0$
and $V\equiv 0$![]() is well known, so we prove our results when $\Omega =\mathbb {R}^N$
is well known, so we prove our results when $\Omega =\mathbb {R}^N$![]() and $V\equiv 0$
and $V\equiv 0$![]() does not occur.
does not occur.
Proof Proof of Theorem 1.1
Let us recall the values
By propositions 4.1 and 1.4 (see (2.11)), and by lemma 4.8, we have that for all $r>\max \{\bar {r},\widehat {r}\}$![]()
We claim that the functional $E$![]() has a (PS)-sequence in $[C_0,{\mathcal {A}}_r]$
has a (PS)-sequence in $[C_0,{\mathcal {A}}_r]$![]() . This done, the existence of a critical point $\bar u$
. This done, the existence of a critical point $\bar u$![]() of $E$
of $E$![]() on $S_{\rho }$
on $S_{\rho }$![]() with $E(\bar u)\le {\mathcal {A}}_r$
with $E(\bar u)\le {\mathcal {A}}_r$![]() follows from proposition 3.1.
follows from proposition 3.1.
Assume, by contradiction, that no (PS)-sequence exists in $[C_0,{\mathcal {A}}_r]$![]() . Then, usual deformation arguments imply the existence of $\eta >0$
. Then, usual deformation arguments imply the existence of $\eta >0$![]() such that the sublevel $E^{C_0-\eta }:=\{u\in H^1_0(\Omega ):\quad |u|_2^2=\rho ^2,\, E(u)\leq C_0-\eta \}$
such that the sublevel $E^{C_0-\eta }:=\{u\in H^1_0(\Omega ):\quad |u|_2^2=\rho ^2,\, E(u)\leq C_0-\eta \}$![]() is a deformation retract of the sublevel $E^{{\mathcal {A}}_r}:=\{u\in H^1_0(\Omega ):\quad |u|_2^2=\rho ^2,\, E(u)\leq {\mathcal {A}}_r\}$
is a deformation retract of the sublevel $E^{{\mathcal {A}}_r}:=\{u\in H^1_0(\Omega ):\quad |u|_2^2=\rho ^2,\, E(u)\leq {\mathcal {A}}_r\}$![]() , namely there exists a continuous function $\varphi :E^{{\mathcal {A}}_r}\to E^{C_0-\eta }$
, namely there exists a continuous function $\varphi :E^{{\mathcal {A}}_r}\to E^{C_0-\eta }$![]() such that
such that
Furthermore, by (5.4) we can also assume $\eta$![]() so small that
so small that
Let us define the map ${\mathcal {H}}:[0,1]\times \Sigma \to \mathbb {R}^N$![]() by
by
By (5.6), (5.5), and by using the map ${\mathcal {G}}$![]() introduced in (4.42), we deduce that ${\mathcal {H}}$
introduced in (4.42), we deduce that ${\mathcal {H}}$![]() maps $\{1\}\times \Sigma$
maps $\{1\}\times \Sigma$![]() in a set homotopically equivalent to $\Sigma$
in a set homotopically equivalent to $\Sigma$![]() in $\mathbb {R}^N\setminus \{0\}$
in $\mathbb {R}^N\setminus \{0\}$![]() . Since ${\mathcal {H}}$
. Since ${\mathcal {H}}$![]() is a continuous map, and arguing exactly as for (4.43), we get the existence of a point $(\tilde t,\tilde z)\in [0,1]\times \Sigma$
is a continuous map, and arguing exactly as for (4.43), we get the existence of a point $(\tilde t,\tilde z)\in [0,1]\times \Sigma$![]() such that
such that
Then by the definition of $C_0$![]() we see $E(\varphi (\psi _r[\tilde t,\tilde z]))\ge C_0$
we see $E(\varphi (\psi _r[\tilde t,\tilde z]))\ge C_0$![]() , contrary to $\varphi (\psi _r[t,z])\in E^{C_0-\eta }$
, contrary to $\varphi (\psi _r[t,z])\in E^{C_0-\eta }$![]() for every $(t,z)\in [0,1]\times \Sigma$
for every $(t,z)\in [0,1]\times \Sigma$![]() , so the claim must be true.
, so the claim must be true.
Finally, since $E(\bar u)\in (m,2^{-s}m)$![]() then $\bar u$
then $\bar u$![]() has constant sign by proposition 2.2. Observe that since $\bar u$
has constant sign by proposition 2.2. Observe that since $\bar u$![]() solves (P) if and only if $-\bar u$
solves (P) if and only if $-\bar u$![]() solves (P), then we have a nonnegative solution.
solves (P), then we have a nonnegative solution.
Proof Proof of Theorem 1.2
This proof proceed in two different ways, according to $\Omega \neq \mathbb {R}^N$![]() or $\Omega =\mathbb {R}^N$
or $\Omega =\mathbb {R}^N$![]() . In both cases, we identify a topological configuration analogous to the one employed in the proof of theorem 1.1 to get the solution. We only outline the procedure, because the argument is the same already developed in details.
. In both cases, we identify a topological configuration analogous to the one employed in the proof of theorem 1.1 to get the solution. We only outline the procedure, because the argument is the same already developed in details.
Case $\Omega \neq \mathbb {R}^N$![]() .
.
Let us apply proposition 4.1, lemma 4.7 and lemma 4.8 with $V\equiv 0$![]() . Then for a fixed $r>0$
. Then for a fixed $r>0$![]() , large enough, we get
, large enough, we get
where ${\mathcal {L}}_{r,0}, C_{0,0},\ {\mathcal {A}}_{r,0}$![]() are defined as in (5.1), (5.2), (5.3), with the functional $E$
are defined as in (5.1), (5.2), (5.3), with the functional $E$![]() replaced by
replaced by
The configuration in (5.7) depends on $\Omega$![]() and $\rho$
and $\rho$![]() .
.
Now, observe that ${\mathcal {L}}_{r,0}\le {\mathcal {L}}_{r}$![]() , $C_{0,0}\le C_{0}$
, $C_{0,0}\le C_{0}$![]() , ${\mathcal {A}}_{r,0}\le {\mathcal {A}}_{r}$
, ${\mathcal {A}}_{r,0}\le {\mathcal {A}}_{r}$![]() , by (1.1). Moreover, by the Hölder inequality and (2.9), it follows that
, by (1.1). Moreover, by the Hölder inequality and (2.9), it follows that
uniformly in $t\in [0,1]$![]() and $z\in \Sigma$
and $z\in \Sigma$![]() , that implies
, that implies
Hence, taking also into account lemma 4.8, we see that there exists $L=L(\Omega,\rho )$![]() such that if $|V|_q< L$
such that if $|V|_q< L$![]() then the configuration (5.4) is restored. In particular,
then the configuration (5.4) is restored. In particular,

As a consequence, if $|V|_q< L$![]() we get a critical value for $E$
we get a critical value for $E$![]() constrained on $S_\rho$
constrained on $S_\rho$![]() , in the energy range $(m,2^{-s}m)$
, in the energy range $(m,2^{-s}m)$![]() .
.
Again, since the solution $\bar u$![]() we have found verifies $E(\bar u)\in (m,2^{-s}m)$
we have found verifies $E(\bar u)\in (m,2^{-s}m)$![]() , it is a constant sign solution by proposition 2.2.
, it is a constant sign solution by proposition 2.2.
Case $\Omega =\mathbb {R}^N$![]() .
.
Let $r>0$![]() and let us introduce the values
and let us introduce the values
Then it turns out that for every fixed $V$![]() there exists $r_V>0$
there exists $r_V>0$![]() such that for every $r> r_V$
such that for every $r> r_V$![]()
By Hölder inequality, for every $y\in \mathbb {R}^N$![]()
Hence, $\widetilde{\mathcal{A}}_r<2^{-s}m$![]() provided
provided
After some computation, by (2.7) with 1 in place of $\rho$![]() and $\rho ^2$
and $\rho ^2$![]() in place of $k$
in place of $k$![]() , we see that (5.12) is equivalent to
, we see that (5.12) is equivalent to
for a suitable constant $c>0$![]() depending on $N,p$
depending on $N,p$![]() and $q$
and $q$![]() . Hence, setting for example
. Hence, setting for example
if $|V|_q< L$![]() then the inequalities (5.11) can be completed as
then the inequalities (5.11) can be completed as
Moreover, by (5.13) we obtain (1.7) and (1.8). Finally, by (5.15) we can argue as in the proof of theorem 1.1 to get the solution we are looking for.
Remark 5.1 Let $\rho >0$![]() be fixed. Arguing as in [Reference Molle and Passaseo32, Theorem 3.1], it is possible to verify that
be fixed. Arguing as in [Reference Molle and Passaseo32, Theorem 3.1], it is possible to verify that
(see(1.9)). Then by $C_{0,0}\le {\mathcal {A}}_{r,0}<2^{-s}m$![]() and (5.8) we obtain
and (5.8) we obtain
6. The case ${\rm N}=1$
In this section we consider the 1-dimensional case

where we can consider $I=\mathbb {R}$![]() or $I=(0,\infty )$
or $I=(0,\infty )$![]() , $V\in L^q(I)$
, $V\in L^q(I)$![]() for some $q\in [1,\infty ]$
for some $q\in [1,\infty ]$![]() , $V\ge 0$
, $V\ge 0$![]() and $2< p<6$
and $2< p<6$![]() .
.
First, let us consider the entire case. For $N=1$![]() , in the asymptotic behaviour of the limit function $w$
, in the asymptotic behaviour of the limit function $w$![]() (see (2.3) and (2.4)) we cannot take advantage of the polinomial contribution provided by $|x|^{\frac {N-1}{2}}$
(see (2.3) and (2.4)) we cannot take advantage of the polinomial contribution provided by $|x|^{\frac {N-1}{2}}$![]() . As a consequence, the key estimate (4.3) in proposition 4.1 does not hold and theorem 1.1 fails.
. As a consequence, the key estimate (4.3) in proposition 4.1 does not hold and theorem 1.1 fails.
On the other hand, theorem 1.2 does not need proposition 4.1 and it can be again stated:
Theorem 6.1 Let $I=\mathbb {R},$![]() $\rho >0,$
$\rho >0,$![]() $V\in L^q(\mathbb {R}),$
$V\in L^q(\mathbb {R}),$![]() for $q\in [1,+\infty ]$
for $q\in [1,+\infty ]$![]() , and $V\ge 0$
, and $V\ge 0$![]() in $\mathbb {R},$
in $\mathbb {R},$![]() then there exists a constant $L=L(\rho )>0$
then there exists a constant $L=L(\rho )>0$![]() such that if $|V|_q< L$
such that if $|V|_q< L$![]() then problem (P 1) has a positive solution.
then problem (P 1) has a positive solution.
Sketch of the proof. This theorem can be proved exactly as theorem 1.2-case $\Omega =\mathbb {R}^N$![]() : we introduce $\widetilde {\mathcal {A}}_r$
: we introduce $\widetilde {\mathcal {A}}_r$![]() , $C_0$
, $C_0$![]() and $\widetilde {\mathcal {L}}_r$
and $\widetilde {\mathcal {L}}_r$![]() (see (5.9), (5.3) and (5.10)) and then observe that for $|V|_q$
(see (5.9), (5.3) and (5.10)) and then observe that for $|V|_q$![]() small $m <\widetilde {\mathcal {L}}_r< C_0\le \widetilde {\mathcal {A}}_r<2^{-s}m$
small $m <\widetilde {\mathcal {L}}_r< C_0\le \widetilde {\mathcal {A}}_r<2^{-s}m$![]() . So, by proposition 3.1, we can argue by deformation as in the proof of theorem 1.1, getting the existence of a nonnegative solution $\bar u$
. So, by proposition 3.1, we can argue by deformation as in the proof of theorem 1.1, getting the existence of a nonnegative solution $\bar u$![]() . By proposition 1.3, the solution $\bar u$
. By proposition 1.3, the solution $\bar u$![]() is positive.
is positive.
According to the exterior case, that is $I=(0,\infty )$![]() , first let us state some nonexistence results.
, first let us state some nonexistence results.
Remark 6.2 If $I=(0,+\infty )$![]() and $V(x)\equiv 0$
and $V(x)\equiv 0$![]() , then the autonomous problem (P 1) has no solution.
, then the autonomous problem (P 1) has no solution.
Indeed, if $u$![]() is a solution of (P 1), then it is a regular free solution of an equation of the form $-u''=f(u)$
is a solution of (P 1), then it is a regular free solution of an equation of the form $-u''=f(u)$![]() , $u(0)=0$
, $u(0)=0$![]() , where $f(u)=-\lambda u+ |u|^{p-2}u$
, where $f(u)=-\lambda u+ |u|^{p-2}u$![]() . Then $u\equiv 0$
. Then $u\equiv 0$![]() by [Reference Esteban and Lions20, Remark I.3], contrary to $u\in S_\rho$
by [Reference Esteban and Lions20, Remark I.3], contrary to $u\in S_\rho$![]() .
.
Proposition 6.3 Let $I=\mathbb {R}$![]() or $I=(0,\infty )$
or $I=(0,\infty )$![]() . If $V\in L^\infty (I)$
. If $V\in L^\infty (I)$![]() is a monotone locally Lipshitz function such that $V'\neq 0$
is a monotone locally Lipshitz function such that $V'\neq 0$![]() on a set of positive measure, then problem (P 1) has no solution.
on a set of positive measure, then problem (P 1) has no solution.
Proposition 6.3 is a simplified version of proposition 1.5 in the 1-dimensional case, adapted also to half lines.
Proof We are assuming $V$![]() non increasing and $I=(0,\infty )$
non increasing and $I=(0,\infty )$![]() .
.
Suppose by contradiction that there exists a solution $u$![]() of (P 1). Since the solutions of (P 1) are in $H^2(I)$
of (P 1). Since the solutions of (P 1) are in $H^2(I)$![]() , we can consider a sequence $(u_n)_n$
, we can consider a sequence $(u_n)_n$![]() in ${\mathcal {C}}^\infty _0((1/n,\infty ))$
in ${\mathcal {C}}^\infty _0((1/n,\infty ))$![]() such that $u_n\to u$
such that $u_n\to u$![]() in $H^2(I)$
in $H^2(I)$![]() . For every $n\in \mathbb {N}$
. For every $n\in \mathbb {N}$![]() , the map $t\mapsto u_n(x+t)$
, the map $t\mapsto u_n(x+t)$![]() , $t\in (-1/n,\infty )$
, $t\in (-1/n,\infty )$![]() , turns out to be a smooth curve in $H^1(I)$
, turns out to be a smooth curve in $H^1(I)$![]() and we can consider the regular map $t\mapsto f_n(t):=E(u_n(x+t))$
and we can consider the regular map $t\mapsto f_n(t):=E(u_n(x+t))$![]() . Since $u$
. Since $u$![]() is a solution of (P 1), we have
is a solution of (P 1), we have
From the monotonicity of $V$![]() and Fatou's lemma we infer
and Fatou's lemma we infer

Letting $n\to \infty$![]() in (6.1) and (6.2), we obtain
in (6.1) and (6.2), we obtain
that is a contradiction. Indeed, by assumption $V'\le 0$![]() a.e. in $I$
a.e. in $I$![]() and $V'<0$
and $V'<0$![]() on a set of positive measure, while $|\{x\in I\, :\, u(x)=0\}|=0$
on a set of positive measure, while $|\{x\in I\, :\, u(x)=0\}|=0$![]() because $u(x)=0$
because $u(x)=0$![]() implies $u'(x)\neq 0$
implies $u'(x)\neq 0$![]() otherwise $u\equiv 0$
otherwise $u\equiv 0$![]() by the Cauchy-Lipschitz theorem.
by the Cauchy-Lipschitz theorem.
If $I=\mathbb {R}$![]() we can proceed in a similar way.
we can proceed in a similar way.
Remark 6.4 In the proof of proposition 6.3, we cannot consider directly the curve in $H^1_0(I)$![]() defined by $\gamma (t):=u(\cdot +t)$
defined by $\gamma (t):=u(\cdot +t)$![]() , $t\ge 0$
, $t\ge 0$![]() . Indeed, $u'(0)\neq 0$
. Indeed, $u'(0)\neq 0$![]() prevents $u'\in H^1_0(I)$
prevents $u'\in H^1_0(I)$![]() , so $\gamma$
, so $\gamma$![]() would be not a regular curve in $H^1_0(I)$
would be not a regular curve in $H^1_0(I)$![]() .
.
Finally, let us state an existence result on half lines, that inherits the topological structure of the entire case.
Theorem 6.5 Let $I=(0,\infty )$![]() , $\rho >0$
, $\rho >0$![]() , $V\in L^q(\mathbb {R})$
, $V\in L^q(\mathbb {R})$![]() , for some $q\in [1,+\infty ]$
, for some $q\in [1,+\infty ]$![]() and $V\ge 0$
and $V\ge 0$![]() . If $|V|_q< L$
. If $|V|_q< L$![]() , with $L$
, with $L$![]() as in theorem 6.1, then there exists $\bar R=\bar R(V,\rho )>0$
as in theorem 6.1, then there exists $\bar R=\bar R(V,\rho )>0$![]() such that problem (P 1) with $V(x-R)$
such that problem (P 1) with $V(x-R)$![]() has a positive solution for every $R>\bar R$
has a positive solution for every $R>\bar R$![]() .
.
Proof In order to get a solution, we are going to solve (P 1) with $V$![]() fixed, on $H^1_0((-R,\infty ))$
fixed, on $H^1_0((-R,\infty ))$![]() .
.
Let us consider (P 1) on $H^1 (\mathbb {R})$![]() , with $V$
, with $V$![]() fixed, and let us define $\widetilde {\mathcal {A}}_r$
fixed, and let us define $\widetilde {\mathcal {A}}_r$![]() , $C_0$
, $C_0$![]() and $\widetilde {\mathcal {L}}_r$
and $\widetilde {\mathcal {L}}_r$![]() as in the proof of theorem 6.1. Moreover, let us fix a cut-off function $\widetilde \vartheta \in C^\infty (\mathbb {R},[0,1])$
as in the proof of theorem 6.1. Moreover, let us fix a cut-off function $\widetilde \vartheta \in C^\infty (\mathbb {R},[0,1])$![]() such that $\widetilde \vartheta (x)=0$
such that $\widetilde \vartheta (x)=0$![]() $\forall x\in (-\infty,0)$
$\forall x\in (-\infty,0)$![]() , $\widetilde \vartheta (x)=1$
, $\widetilde \vartheta (x)=1$![]() $\forall x\in (1,\infty )$
$\forall x\in (1,\infty )$![]() and introduce
and introduce

Then,
Hence, for large $R$![]() , we get
, we get
and we can argue as in the proof of theorem 1.1, by proposition 3.1.
Data
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Acknowledgements
The authors thank the anonymous referee for bringing to their attention some recent papers and for useful suggestions.
Financial support
The authors have been supported by the INdAM-GNAMPA group; R.M. acknowledges also the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome ‘Tor Vergata’, CUP E83C23000330006.
Ethical Standards
We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
Appendix
The following proof could be shortened by taking into account, for example, Lemma B.3 in [Reference Struwe39]. We develop some more details on the bootstrap procedure, for the sake of completeness.
For classical regularity results, we refer the reader for example to [Reference Lieb and Loss30, §10], and in particular Theorem 10.2 therein, or to [Reference Gilbarg and Trudinger23, §8].
Proof Proof of proposition 1.3
$(a)$![]() Once proved $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$
Once proved $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$![]() we are done. Indeed, when $q>\frac N2$
we are done. Indeed, when $q>\frac N2$![]() we can apply the Harnack inequality and conclude that the nonnegative solutions are actually strictly positive in $\Omega$
we can apply the Harnack inequality and conclude that the nonnegative solutions are actually strictly positive in $\Omega$![]() (see [Reference Pucci and Serrin36, Theorem 7.2.1]).
(see [Reference Pucci and Serrin36, Theorem 7.2.1]).
To verify that $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$![]() , we begin by observing that the function $\bar u$
, we begin by observing that the function $\bar u$![]() verifies
verifies
Since $V\in L^q_{\mathop {\rm loc}\nolimits }(\Omega )$![]() with $q>N/2$
with $q>N/2$![]() , we have that $\psi \in L^{q_1}_{\mathop {\rm loc}\nolimits }(\Omega )$
, we have that $\psi \in L^{q_1}_{\mathop {\rm loc}\nolimits }(\Omega )$![]() with
with
Notice also that $q_1>\frac {N}{2}$![]() because $p<2^*$
because $p<2^*$![]() . By Hölder inequality, $\psi \bar u\in L^{r_1}_{\mathop {\rm loc}\nolimits }(\Omega )$
. By Hölder inequality, $\psi \bar u\in L^{r_1}_{\mathop {\rm loc}\nolimits }(\Omega )$![]() with $r_1$
with $r_1$![]() defined by
defined by
By regularity results, we have that:
$(1)$
 if $r_1>\frac {N}{2}$
if $r_1>\frac {N}{2}$ , then $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$
, then $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$ with $\alpha <2-\frac {N}{r_1}$
with $\alpha <2-\frac {N}{r_1}$ ;
;$(2)$
 if $r_1=\frac N2$
if $r_1=\frac N2$ , then $\bar u\in L^s_{\mathop {\rm loc}\nolimits }(\Omega )$
, then $\bar u\in L^s_{\mathop {\rm loc}\nolimits }(\Omega )$ $\forall s>1$
$\forall s>1$ ;
;$(3)$
 if $r_1<\frac {N}{2}$
if $r_1<\frac {N}{2}$ , then $\bar u\in L^{r_1N/(N-2r_1)}_{\mathop {\rm loc}\nolimits }(\Omega )$
, then $\bar u\in L^{r_1N/(N-2r_1)}_{\mathop {\rm loc}\nolimits }(\Omega )$ .
.
In case (1) the assertion is proved.
In case (2) it is readily seen that $\psi \, \bar u\in L^{s_1}_{\mathop {\rm loc}\nolimits }(\Omega )$![]() for every $1\le s_1< q$
for every $1\le s_1< q$![]() . Hence we can conclude as in the previous case, choosing $N/2< s_1< q$
. Hence we can conclude as in the previous case, choosing $N/2< s_1< q$![]() .
.
If (3) holds, then $\psi \in L^{q_2}_{\mathop {\rm loc}\nolimits }(\Omega )$![]() , with
, with
Since $q_1>\frac {N}{2}$![]() , we get $\frac {r_1 N}{N-2r_1}>\frac {2N}{N-2}$
, we get $\frac {r_1 N}{N-2r_1}>\frac {2N}{N-2}$![]() and hence $q_2\geq q_1$
and hence $q_2\geq q_1$![]() .
.
Now, repeating the same argument of the previous step, by Hölder inequality $\psi \bar u\in L^{r_2}_{\mathop {\rm loc}\nolimits }(\mathbb {R}^N)$![]() with $r_2$
with $r_2$![]() defined by
defined by
and again we have
$(4)$
 if $r_2\ge \frac {N}{2}$
if $r_2\ge \frac {N}{2}$ , then $\bar u\in {\mathcal{C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$
, then $\bar u\in {\mathcal{C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$ ;
;$(5)$
 if $r_2<\frac {N}{2}$
if $r_2<\frac {N}{2}$ , then $\bar u\in L^{r_2N/(N-2r_2)}_{\mathop {\rm loc}\nolimits }(\Omega )$
, then $\bar u\in L^{r_2N/(N-2r_2)}_{\mathop {\rm loc}\nolimits }(\Omega )$ .
.
Observe that $r_2>r_1$![]() because $q_2\geq q_1$
because $q_2\geq q_1$![]() and $\frac {r_1 N}{N-2r_1}>\frac {2N}{N-2}$
and $\frac {r_1 N}{N-2r_1}>\frac {2N}{N-2}$![]() .
.
Iterating this bootstrap argument, we claim that, after $\bar k$![]() steps, $r_{\bar k}\ge \frac N2$
steps, $r_{\bar k}\ge \frac N2$![]() , so that we are done. If, by contradiction, the claim is false, then for every integer $k$
, so that we are done. If, by contradiction, the claim is false, then for every integer $k$![]() we define
we define
Inductively, it turns out that $q_k\geq q_{k-1}$![]() and $r_k>r_{k-1}$
and $r_k>r_{k-1}$![]() , for any $k\in \mathbb {N}$
, for any $k\in \mathbb {N}$![]() , with $q_k\le q$
, with $q_k\le q$![]() and $r_k<\frac N2$
and $r_k<\frac N2$![]() . Let us set
. Let us set
Getting $k\to \infty$![]() in (A.2) we obtain
in (A.2) we obtain
that implies $Q=\frac {N}{2}$![]() , contrary to $Q\geq q_1>\frac {N}{2}$
, contrary to $Q\geq q_1>\frac {N}{2}$![]() . So, a contradiction arises and $(a)$
. So, a contradiction arises and $(a)$![]() is proved.
is proved.
$(b)$![]() The function $\bar u$
The function $\bar u$![]() verifies
verifies
If $V\in L^q_{\mathop {\rm loc}\nolimits }(\Omega )$![]() , with $q>N$
, with $q>N$![]() , then $\bar u\in L^\infty _{\mathop {\rm loc}\nolimits }(\Omega )$
, then $\bar u\in L^\infty _{\mathop {\rm loc}\nolimits }(\Omega )$![]() , by $(a)$
, by $(a)$![]() , and so $\phi \in L^q_{\mathop {\rm loc}\nolimits }(\Omega )$
, and so $\phi \in L^q_{\mathop {\rm loc}\nolimits }(\Omega )$![]() , that allows us to deduce $\bar u\in {\mathcal{C}}^{1,\alpha }(\Omega )$
, that allows us to deduce $\bar u\in {\mathcal{C}}^{1,\alpha }(\Omega )$![]() .
.
$(c)$![]() This point follows by classical regularity results.
This point follows by classical regularity results.
$(d)$![]() By classical regularity results, $\bar u$
By classical regularity results, $\bar u$![]() is continuously differentiable. If $\bar u$
is continuously differentiable. If $\bar u$![]() is nonnegative, then it turns out to be positive, by the Harnack inequality (see [Reference Pucci and Serrin36, Theorem 7.2.1]).
is nonnegative, then it turns out to be positive, by the Harnack inequality (see [Reference Pucci and Serrin36, Theorem 7.2.1]).
$(e)$![]() By a direct verification on (P 1), we see that there exists $\bar u''$
By a direct verification on (P 1), we see that there exists $\bar u''$![]() in $L^{q}(\Omega )$
in $L^{q}(\Omega )$![]() , in a weak sense. Hence, if $q<2$
, in a weak sense. Hence, if $q<2$![]() then $\bar u'\in W^{1,q}_{\mathop {\rm loc}\nolimits }(\Omega )$
then $\bar u'\in W^{1,q}_{\mathop {\rm loc}\nolimits }(\Omega )$![]() and if $q\ge 2$
and if $q\ge 2$![]() then $\bar u'\in H^1_{\mathop {\rm loc}\nolimits }(\Omega )$
then $\bar u'\in H^1_{\mathop {\rm loc}\nolimits }(\Omega )$![]() . In any case, we can conclude that $\bar u'\in {\mathcal{C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$
. In any case, we can conclude that $\bar u'\in {\mathcal{C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\Omega )$![]() , so the proof is complete.
, so the proof is complete.