Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-19T15:10:36.772Z Has data issue: false hasContentIssue false
  • English
  • Français

The mod-p homology of the classifying spaces of certain gauge groups

Part of: Quantum field theory; related classical field theories Fiber spaces and bundles

Published online by Cambridge University Press:  19 September 2022

Daisuke Kishimoto  and
Stephen Theriault
Daisuke Kishimoto
Affiliation:
Faculty of Mathematics, Kyushu University, Fukuoka, 819-0395, Japan ([email protected])
Stephen Theriault
Affiliation:
Mathematical Sciences, University of Southampton, Southampton SO17 1BJ, United Kingdom ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

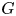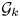Let $G$ be a compact connected simple Lie group of type $(n_{1},\,\ldots,\,n_{l})$, where $n_{1}<\cdots < n_{l}$. Let $\mathcal {G}_k$ be the gauge group of the principal $G$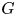-bundle over $S^{4}$ 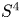corresponding to $k\in \pi _3(G)\cong \mathbb {Z}$. We calculate the mod-$p$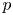 homology of the classifying space $B\mathcal {G}_k$ 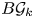provided that $n_{l}< p-1$.

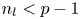Keywords

Gauge groupclassifying spacehomology

MSC classification

Primary: 55R40: Homology of classifying spaces, characteristic classes
Secondary: 81T13: Yang-Mills and other gauge theories
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 6 , December 2023 , pp. 1805 - 1817
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atiyah, M. F. and Bott, R.. The Yang-Mills equations over Riemann surfaces. Philos. Trans. Roy. Soc. London Ser. A 308 (1983), 523–615.Google Scholar
Atiyah, M. F. and Jones, J. D. S.. Topological aspects of Yang-Mills theory. Commun. Math. Phys. 61 (1978), 97–118.CrossRefGoogle Scholar
Choi, Y.. Homology of the classifying space of $Sp(n)$ gauge groups. Israel J. Math. 151 (2006), 167–177.CrossRefGoogle Scholar
Cohen, F. R., Lada, T. J. and May, J. P.. The homology of iterated loop spaces, Lecture Notes in Math. Vol. 533 (Springer-Verlag, 1976).CrossRefGoogle Scholar
Donaldson, S. K.. Connections, cohomology and the intersection forms on $4$-manifolds. J. Differ. Geom. 24 (1986), 275–341.Google Scholar
Floer, A.. An instanton invariant for $3$-manifolds. Commun. Math. Phys. 118 (1988), 215–240.CrossRefGoogle Scholar
Gottlieb, D. H.. Applications of bundle map theory. Trans. Amer. Math. Soc. 171 (1972), 23–50.CrossRefGoogle Scholar
Gray, B. and Theriault, S.. An elementary construction of Anick's fibration. Geom. Topol. 14 (2010), 243–276.CrossRefGoogle Scholar
Hasui, S., Kishimoto, D. and Ohsita, A.. Samelson products in $p$-regular exceptional Lie groups. Topology Appl. 178 (2014), 17–29.CrossRefGoogle Scholar
Kaji, S. and Kishimoto, D.. Homotopy nilpotency in $p$-regular loop spaces. Math. Z. 264 (2010), 209–224.CrossRefGoogle Scholar
Kishimoto, D. and Kono, A.. Splitting of gauge groups. Trans. Amer. Math. Soc. 362 (2010), 6715–6731.CrossRefGoogle Scholar
Kishimoto, D. and Tsutaya, M.. Infiniteness of $A_\infty$-types of gauge groups. J. Topol. 9 (2016), 181–191.CrossRefGoogle Scholar
Kishimoto, D. and Tsutaya, M.. Samelson products in $p$-regular $\mathrm {SO}(2n)$ and its homotopy normality. Glasg. Math. J. 60 (2018), 165–174.CrossRefGoogle Scholar
Kono, A.. A note on the homotopy type of certain gauge groups. Proc. Roy. Soc. Edinburgh Sect. A 117 (1991), 295–297.CrossRefGoogle Scholar
Lang, G. E.. The evaluation map and $EHP$ sequences. Pacific J. Math. 44 (1973), 201–210.CrossRefGoogle Scholar
Masbaum, G.. On the cohomology of the classifying space of the gauge group over some $4$-complexes. Bull. Soc. Math. France 119 (1991), 1–31.CrossRefGoogle Scholar
McGibbon, C. A.. Homotopy commutativity in localized groups. Amer. J. Math. 106 (1984), 665–687.CrossRefGoogle Scholar
Selick, P. S.. A reformulation of the Arf invariant one mod-$p$ problem and applications to atomic spaces. Pacific J. Math. 108 (1983), 431–450.CrossRefGoogle Scholar
Theriault, S. D.. Atomicity for Anick's spaces. J. Pure Appl. Alg. 219 (2015), 2346–2358.CrossRefGoogle Scholar
Toda, H.. Composition methods in homotopy groups of spheres, Annals of Math. Studies No. Vol. 49 (Princeton University Press, Princeton NJ, 1962).Google Scholar