Hostname: page-component-6bf8c574d5-h6jzd Total loading time: 0.001 Render date: 2025-02-19T19:57:54.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Large deviation principle for slow-fast rough differential equations via controlled rough paths

Part of: Stochastic processes Limit theorems

Published online by Cambridge University Press:  28 January 2025

Xiaoyu Yang  and
Yong Xu
Xiaoyu Yang
Affiliation:
Graduate School of Information Science and Technology, Osaka University, Suita, Osaka, 5650871, Japan ([email protected])
Yong Xu*
Affiliation:
School of Mathematics and Statistics, Northwestern Polytechnical University, Xi’an, Shaanxi, 710072, China MOE Key Laboratory of Complexity Science in Aerospace, Northwestern Polytechnical University, Xi’an, Shaanxi, 710072, China ([email protected]) (corresponding author)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a large deviation principle for the slow-fast rough differential equations (RDEs) under the controlled rough path (RP) framework. The driver RPs are lifted from the mixed fractional Brownian motion (FBM) with Hurst parameter 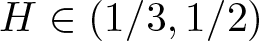$H\in (1/3,1/2)$. Our approach is based on the continuity of the solution mapping and the variational framework for mixed FBM. By utilizing the variational representation, our problem is transformed into a qualitative property of the controlled system. In particular, the fast RDE coincides with Itô stochastic differential equation (SDE) almost surely, which possesses a unique invariant probability measure with frozen slow component. We then demonstrate the weak convergence of the controlled slow component by averaging with respect to the invariant measure of the fast equation and exploiting the continuity of the solution mapping.

Keywords

rough pathsfractional Brownian motionlarge deviation principleslow-fast systemweak convergence

MSC classification

Secondary: 60F10: Large deviations 60G22: Fractional processes, including fractional Brownian motion
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 31
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bardi, M., Cesaroni, A. and Scotti, A.. Convergence in multiscale financial models with non-Gaussian stochastic volatility. ESAIM - Control Optim. Calc. Var. 22(2) (2016), 500–518.CrossRefGoogle Scholar
Biagini, F., Hu, Y. Z., Oksendal, B. and Zhang, T. S.. Stochastic calculus for fractional Brownian motion and applications (Springer Science & Business Media, 2008).CrossRefGoogle Scholar
Boué, M. and Dupuis, P.. A variational representation for certain functionals of Brownian motion. Ann. Probab. 26(4) (1998), 1641–1659.CrossRefGoogle Scholar
Bourguin, S., Gailus, S. and Spiliopoulos, K.. Discrete-time inference for slow-fast systems driven by fractional Brownian motion. Multiscale Model. Simul. 19(3) (2021), 1333–1366.CrossRefGoogle Scholar
Budhiraja, A. and Dupuis, P.. Analysis and approximation of rare events. Representations and weak convergence methods, Series Probability Theory and Stochastic Modelling, Volume 94 (Springer, 2019).Google Scholar
Budhiraja, A., Dupuis, P. and Maroulas, V.. Variational representations for continuous time processes. Ann. Inst. Henri Poincare (B) Probab. Stat. 47(3) (2011), 725–747.CrossRefGoogle Scholar
Budhiraja, A. and Song, X. M.. Large deviation principles for stochastic dynamical systems with a fractional Brownian noise. (2020), arXiv preprint arXiv:2006.07683.Google Scholar
Cerrai, S. and Röckner, M.. Large deviations for stochastic reaction-diffusion systems with multiplicative noise and non-Lipshitz reaction term. Ann. Probab. 32(1B) (2004), 1100–1139.CrossRefGoogle Scholar
Ciesielski, Z.. On the isomorphism of the spaces $H_{\alpha}$ and m. Bulietin De L’Academie Polonaise Des Sciences, Séris Des Sci, Math. Astr. Et Phys. 8(4) (1960), 217–222.Google Scholar
Decreusefond, L. and Ustnel, A. S.. Stochastic analysis of the fractional Brownian motion. Potential Anal. 10(2) (1999), 177–214.CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O.. Large deviations techniques and applications (Springer Science & Business Media, 2009).Google Scholar
Dupuis, P. and Ellis, R.. A weak convergence approach to the theory of large deviations (John Wiley & Sons, 2011).Google Scholar
Dupuis, P. and Spiliopoulos, K.. Large deviations for multiscale diffusion via weak convergence methods. Stoch. Process. Appl. 4 (2012), 1947–1987.CrossRefGoogle Scholar
Feng, J., Fouque, J. P. and Kumar, R.. Small-time asymptotics for fast mean-reverting stochastic volatility models. Ann. Appl. Probab. 22(2) (2012), 1541–1575.CrossRefGoogle Scholar
Feng, J. and Kurtz, T. G.. Large deviation for stochastic processes (American Mathematical Society, 2006).CrossRefGoogle Scholar
Friz, P. and Hairer, M.. A course on rough paths (Springer International Publishing, 2020).CrossRefGoogle Scholar
Friz, P. and Victoir, N.. A variation embedding theorem and applications. J. Funct. Anal. 2 (2006), 631–637.CrossRefGoogle Scholar
Friz, P. and Victoir, N.. Large deviation principle for enhanced Gaussian processes. Ann. inst. Henri Poincare (B) Probab. Stat. 43(6) (2007), 775–785.CrossRefGoogle Scholar
Friz, P. and Victoir, N.. Multidimensional stochastic processes as rough paths: Theory and applications (Cambridge University Press, 2010).CrossRefGoogle Scholar
Hairer, M. and Li, X. M.. Averaging dynamics driven by fractional Brownian motion. Ann. Probab. 48(4) (2020), 1826–1860.CrossRefGoogle Scholar
Inahama, Y.. Laplace approximation for rough differential equation driven by fractional Brownian motion. Ann. Probab. 41(1) (2013), 170–205.CrossRefGoogle Scholar
Inahama, Y.. Large deviation principle of Freidlin-Wentzell type for pinned diffusion processes. Trans. Am. Math. Soc. 367(11) (2015), 8107–8137.CrossRefGoogle Scholar
Inahama, Y.. Averaging principle for slow-fast systems of rough differential equations via controlled paths. To Appear in Tohoku Mathematical Journal. 44 (2023), pages.Google Scholar
Inahama, Y., Xu, Y. and Yang, X. Y.. Large deviation principle for slow-fast system with mixed fractional Brownian motion. (2023), arXiv preprint arXiv:2303.06626.Google Scholar
Kiefer, Y.. Averaging and climate models, In Stochastic Climate Models (Birkhäuser, Boston, 2000).Google Scholar
Klenke, A.. Probability theory: A comprehensive course. 3rd edn (Springer Science & Business Media, 2020).Google Scholar
Krupa, M., Popović, N. and Kopell, N.. Mixed-mode oscillations in a three time-scale model for the dopaminergic neuron. Interdiscipl. J. Nonlinear Sci. 18(1) (2008), .Google Scholar
Ledoux, M., Qian, Z. M. and Zhang, T. S.. Large deviations and support theorem for diffusion processes via rough paths. Stoch. Process. Appl. 102(2) (2007), 265–283.CrossRefGoogle Scholar
Liu, W., Röckner, M., Sun, X. B., et al. Averaging principle for slow-fast stochastic differential equations with time dependent locally Lipschitz coefficients. J. Differ. Equ. 6 (2020), 2910–2948.CrossRefGoogle Scholar
Liu, Y. H. and Tindel, S.. First-order Euler scheme for SDES driven by fractional Brownian motions. Ann. Appl. Probab. 29(2) (2019), 758–826.CrossRefGoogle Scholar
Lyons, T.. Differential equations driven by rough signals. Rev. Mat. Iberoam. 14(2) (1998), 215–310.CrossRefGoogle Scholar
Lyons, T. and Qian, Z. M.. System control and rough paths (Oxford University Press, 2002).CrossRefGoogle Scholar
Millet, A. and Sanz-Solé, M.. Large deviations for rough paths of the fractional Brownian motion. Annales de l’IHP Probabilités et statistiques. 42(2) (2006), 245–271.Google Scholar
Mishura, Y. S. and Mishura, I. U. S.. Stochastic calculus for fractional Brownian motion and related processes (Springer Science & Business Media, 2008).CrossRefGoogle Scholar
Pavliotis, G. and Stuart, A.. Multiscale methods: Averaging and homogenization (Springer Science & Business Media, 2008).Google Scholar
Pei, B., Inahama, Y. and Xu, Y.. Averaging principles for mixed fast-slow systems driven by fractional Brownian motion. Kyoto J. Math. 63(4) (2023), 721–748.CrossRefGoogle Scholar
Peszat, S.. Large deviation principle for stochastic evolution equations. Probab. Theory Relat. Fields. 98 (1994), 113–136.CrossRefGoogle Scholar
Röckner, M., Xie, L. J. and Yang, L.. Asymptotic behavior of multiscale stochastic partial differential equations with Hölder coefficients. J. Funct. Anal. 9 (2023), .Google Scholar
Rascanu, A.. Differential equations driven by fractional Brownian motion. Collect. Math 53(1) (2002), 55–81.Google Scholar
Sritharan, S. S. and Sundar, P.. Large deviations for the two-dimensional Navier-Stokes equations with multiplicative noise. Stoch. Process. Appl. 11 (2006), 1636–1659.CrossRefGoogle Scholar
Sun, X. B., Wang, R., Xu, L. and Yang, X.. Large deviation for two-time-scale stochastic Burgers equation. Stoch. Dyn. 21(5) (2020), .Google Scholar
Wentzell, D. and Freidlin, I.. Random perturbations of dynamical systems (Springer, 1984).Google Scholar
Yang, X. Y., Xu, Y. and Pei, B.. Precise Laplace approximation for mixed rough differential equation. J. Differ. Equ. 415 (2025), 1–51.CrossRefGoogle Scholar