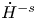Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huo, Wenwen
and
Teng, Kaimin
2022.
Global well-posedness and $$L^2$$ decay estimate of smooth solutions for 2D incompressible Navier–Stokes–Allen–Cahn system.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 73,
Issue. 6,
Huo, Wenwen
Teng, Kaimin
and
Zhang, Chao
2024.
Global well-posedness and L 2 decay estimate of smooth solutions for the 3-D incompressible Navier–Stokes–Allen–Cahn system.
Asymptotic Analysis,
Vol. 139,
Issue. 1-2,
p.
89.
Chen, Ya-zhou
Peng, Yi
and
Shi, Xiao-ding
2024.
Sharp Interface Limit for the One-dimensional Compressible Navier-Stokes/Allen-Cahn System with Composite Waves.
Acta Mathematicae Applicatae Sinica, English Series,
Chen, Yunkun
Huang, Bin
and
Shi, Xiaoding
2024.
Stability of the rarefaction wave in the singular limit of a sharp interface problem for the compressible Navier-Stokes/Allen-Cahn system.
Acta Mathematica Scientia,
Vol. 44,
Issue. 4,
p.
1507.
Chen, Ya-zhou
Hong, Hakho
and
Shi, Xiao-ding
2024.
Stability of the Phase Separation State for Compressible Navier-Stokes/Allen-Cahn System.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 40,
Issue. 1,
p.
45.
Li, Yinghua
Xie, Manrou
and
Yan, Yuanxiang
2025.
Exponential stability of a diffuse interface model of incompressible two-phase flow with phase variable dependent viscosity and vacuum.
Journal of Differential Equations,
Vol. 414,
Issue. ,
p.
842.
Chen, Yazhou
Tang, Houzhi
and
Zhang, Yue
2025.
Wave propagation for the isentropic compressible Navier–Stokes/Allen–Cahn system.
Mathematical Methods in the Applied Sciences,
Vol. 48,
Issue. 3,
p.
2726.