Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-23T23:53:16.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Examples of degenerate symmetric differential operators with infinite deficiency indices in L2(ℝm)

Published online by Cambridge University Press:  14 November 2011

Yurii B. Orochko
Yurii B. Orochko
Affiliation:
Department of Applied Mathematics, Moscow State Institute of Electronics and Mathematics, Moscow 109028, Russia
Get access Rights & Permissions [Opens in a new window]

Extract

For an unbounded self-adjoint operator A in a separable Hilbert space ℌ and scalar real-valued functions a(t), q(t), r(t), t ∊ ℝ, consider the differential expression

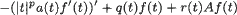
acting on ℌ-valued functions f(t), t ∊ ℝ, and degenerating at t = 0. Let Sp denotethe corresponding minimal symmetric operator in the Hilbert space (ℝ) of ℌ-valued functions f(t) with ℌ-norm ∥f(t)∥ square integrable on the line. The infiniteness of the deficiency indices of Sp, 1/2 < p < 3/2, is proved under natural restrictions on a(t), r(t), q(t). The conditions implying their equality to 0 for p ≥ 3/2 are given. In the case of a self-adjoint differential operator A acting in ℌ = L2(ℝn), the first of these results implies examples of symmetric degenerate differential operators with infinite deficiency indices in L2(ℝm), m = n + 1.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 129 , Issue 1 , 1999 , pp. 165 - 179
Copyright
Copyright © Royal Society of Edinburgh 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Akhiezer, N. I. and Glazman, I. M.. Theory of linear operators in Hilbert space, vols I and II (London and Edinburgh: Pitman and Scottish Academic Press, 1980).Google Scholar
2Behnke, H. and Focke, H.. Deficiency indices of singular Schrödinger operators. Math. Z. 158 (1978), 87–98.CrossRefGoogle Scholar
3Devinatz, A.. Self-adjointness of second order degenerate-elliptic operators. Indiana Univ. Math. J. 27 (1978), 255–266.CrossRefGoogle Scholar
4Dunford, N. and Schwartz, J. T.. Linear operators. Part I. General theory (New York: Wiley Interscience, 1958).Google Scholar
5Dunford, N. and Schwartz, J. T.. Linear operators. Part II. Spectral theory (New York: Wiley Interscience, 1963).Google Scholar
6Everitt, W. N. and Zettl, A.. Differential operators generated by a countable number of quasi-differential expressions on the real line. Proc. Lond. Math. Soc. 64 (1992), 524–544.CrossRefGoogle Scholar
7Gorbachuk, M. L. and Gorbachuk, V. I.. Boundary value problems for operator differential equations (Dordrecht, Boston, London: Kluwer, 1991).CrossRefGoogle Scholar
8Orochko, Yu. B.. The hyperbolic equation method in the theory of operators of Schrödinger type with a locally integrable potential. Russ. Math. Surv. 43(2) (1988), 51–102.CrossRefGoogle Scholar
9Orochko, Yu. B.. Examples of symmetric differential operators with infinite deficiency indices on the line. Funct. Analysis Appl. 28(2) (1994),69–72.Google Scholar
10Reed, M. and Simon, B.. Methods of modern mathematical physics, vol. 2. Fourier analysis, self-adjointness (New York: Academic Press, 1975).Google Scholar
11Titchmarsh, B. C.. Eigenfunction expansions associated with second-order differential equations. Part I (Oxford University Press, 1962).CrossRefGoogle Scholar