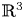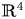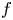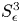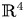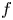1. Introduction
The aim of this paper is to study the topological classification of real analytic map germs $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() with isolated instability of fold type, that is, $f$
with isolated instability of fold type, that is, $f$![]() is of Thom–Boardman type $\Sigma ^{1,0}$
is of Thom–Boardman type $\Sigma ^{1,0}$![]() . This is done by means of the topological type of their associated link, a stable map from $S^{2}$
. This is done by means of the topological type of their associated link, a stable map from $S^{2}$![]() to $S^{3}$
to $S^{3}$![]() obtained by intersecting the image of $f$
obtained by intersecting the image of $f$![]() with a small enough 3-sphere $S_\epsilon ^{3}$
with a small enough 3-sphere $S_\epsilon ^{3}$![]() centred at the origin. We construct a complete topological invariant of this link by defining an associated dual tree, a particular type of graph, which contains all the topological information. We will prove that if $f$
centred at the origin. We construct a complete topological invariant of this link by defining an associated dual tree, a particular type of graph, which contains all the topological information. We will prove that if $f$![]() and $g$
and $g$![]() are of fold type, they are topologically equivalent if and only if the dual trees of their associated links are equivalent. In the last part, as an application, we give a list of all topological classes up to dual trees with 4 vertices and an algorithm to obtain a normal form of the topological class given by any dual tree.
are of fold type, they are topologically equivalent if and only if the dual trees of their associated links are equivalent. In the last part, as an application, we give a list of all topological classes up to dual trees with 4 vertices and an algorithm to obtain a normal form of the topological class given by any dual tree.
The topological classification problem in the case of real analytic map germs from $\mathbb {R}^{n}$![]() to $\mathbb {R}^{p}$
to $\mathbb {R}^{p}$![]() with $n< p$
with $n< p$![]() has been studied by several authors. In [Reference Marar and Nuño Ballesteros8] Marar and the second author give a full topological classification of map germs $f\colon (\mathbb {R}^{2},0)\to (\mathbb {R}^{3},0)$
has been studied by several authors. In [Reference Marar and Nuño Ballesteros8] Marar and the second author give a full topological classification of map germs $f\colon (\mathbb {R}^{2},0)\to (\mathbb {R}^{3},0)$![]() that belong to the 2-jet classes $(x,y^{2},xy), (x,y^{2},0)$
that belong to the 2-jet classes $(x,y^{2},xy), (x,y^{2},0)$![]() and $(x,xy,0)$
and $(x,xy,0)$![]() . To do this they use the Gauss word of the associated link of these map germs as a complete topological invariant. In [Reference Martins and Nuño-Ballesteros9] Martins and the second author also work in this case, classifying all ruled surfaces. In [Reference Mendes and Nuño-Ballesteros11, Reference Mendes and Nuño-Ballesteros12] Mendes and the second author show that the knot type of the link of a real analytic map germ with isolated singularity $f\colon (\mathbb {R}^{2}, 0)\to (\mathbb {R}^{4}, 0)$
. To do this they use the Gauss word of the associated link of these map germs as a complete topological invariant. In [Reference Martins and Nuño-Ballesteros9] Martins and the second author also work in this case, classifying all ruled surfaces. In [Reference Mendes and Nuño-Ballesteros11, Reference Mendes and Nuño-Ballesteros12] Mendes and the second author show that the knot type of the link of a real analytic map germ with isolated singularity $f\colon (\mathbb {R}^{2}, 0)\to (\mathbb {R}^{4}, 0)$![]() is a complete invariant for topological equivalence and show that for a generic projection from $\mathbb {R}^{4}$
is a complete invariant for topological equivalence and show that for a generic projection from $\mathbb {R}^{4}$![]() to $\mathbb {R}^{3}$
to $\mathbb {R}^{3}$![]() , the projection of the knot coincides with the link of the projected singular surface.
, the projection of the knot coincides with the link of the projected singular surface.
If we centre our attention in recent results for map germs $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() , Casonatto, Romero Fuster and Wik Atique have obtained in [Reference Casonatto, Romero Fuster and Wik Atique4, Reference Casonatto, Romero Fuster and Wik Atique5] Vassiliev invariants for stable maps of oriented 3-manifolds in $\mathbb {R}^{4}$
, Casonatto, Romero Fuster and Wik Atique have obtained in [Reference Casonatto, Romero Fuster and Wik Atique4, Reference Casonatto, Romero Fuster and Wik Atique5] Vassiliev invariants for stable maps of oriented 3-manifolds in $\mathbb {R}^{4}$![]() . In the complex case, Houston and Kirk study in [Reference Houston and Kirk7] the corank 1 $\mathcal {A}$
. In the complex case, Houston and Kirk study in [Reference Houston and Kirk7] the corank 1 $\mathcal {A}$![]() -classification.
-classification.
Finally, let us remark that the techniques used in this paper of obtaining the topological classification of real analytic map germs by means of its associated link has been used by both authors and the second author with several collaborators in other cases [Reference Batista, Costa and Nuño Ballesteros1, Reference Batista, Costa and Nuño Ballesteros2, Reference Moya-Pérez and Nuño-Ballesteros15–Reference Moya-Pérez and Nuño-Ballesteros17, Reference Nuño-Ballesteros18].
The paper is organized as follows. In the second section we characterize the notions of stability and finite determinacy of a map germ and define its associated link in our particular case of study. In §3 we obtain a prenormal form for map germs of fold type. In §4 we introduce the notion of mosaic of a 2-disc and its associated dual tree. Section 5 is dedicated to define the notion of the dual tree of a folded stable map from $S^{2}$![]() to $S^{3}$
to $S^{3}$![]() and to prove that it becomes a complete topological invariant (corollary 5.9). We finish the paper obtaining, in §6, as an application, some normal forms (remark 6.1) and indicating how to generalize the procedure (remark 6.2).
and to prove that it becomes a complete topological invariant (corollary 5.9). We finish the paper obtaining, in §6, as an application, some normal forms (remark 6.1) and indicating how to generalize the procedure (remark 6.2).
All map germs considered are real analytic except otherwise stated. We adopt the notation and basic definitions that are usual in singularity theory (e.g. $\mathcal {A}$![]() -equivalence, stability, finite determinacy, etc.), as the reader can find in Wall's survey paper [Reference Wall19] or in the book [Reference Mond and Nuño-Ballesteros14].
-equivalence, stability, finite determinacy, etc.), as the reader can find in Wall's survey paper [Reference Wall19] or in the book [Reference Mond and Nuño-Ballesteros14].
2. Stability, finite determinacy and the link of a germ
In this section we recall the basic definitions and results that we will need, including the characterization of stable maps from $\mathbb {R}^{3}$![]() to $\mathbb {R}^{4}$
to $\mathbb {R}^{4}$![]() , the Mather–Gaffney finite determinacy criterion and the link of a map germ.
, the Mather–Gaffney finite determinacy criterion and the link of a map germ.
Two smooth ($C^{\infty }$![]() ) map germs $f,g\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$
) map germs $f,g\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() are $\mathcal {A}$
are $\mathcal {A}$![]() -equivalent if there exist diffeomorphism germs $\phi \colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{3},0)$
-equivalent if there exist diffeomorphism germs $\phi \colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{3},0)$![]() and $\psi \colon (\mathbb {R}^{4},0)\to (\mathbb {R}^{4},0)$
and $\psi \colon (\mathbb {R}^{4},0)\to (\mathbb {R}^{4},0)$![]() such that $g=\psi \circ f\circ \phi ^{-1}$
such that $g=\psi \circ f\circ \phi ^{-1}$![]() . If $\phi,\psi$
. If $\phi,\psi$![]() are homeomorphisms instead of diffeomorphisms, then we say that $f,g$
are homeomorphisms instead of diffeomorphisms, then we say that $f,g$![]() are topologically equivalent.
are topologically equivalent.
We say that $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() is $k$
is $k$![]() -determined if any map germ $g$
-determined if any map germ $g$![]() with the same $k$
with the same $k$![]() -jet is $\mathcal {A}$
-jet is $\mathcal {A}$![]() -equivalent to $f$
-equivalent to $f$![]() . We say that $f$
. We say that $f$![]() is finitely determined if it is $k$
is finitely determined if it is $k$![]() -determined for some $k$
-determined for some $k$![]() .
.
Let $U\subset \mathbb {R}^{3}$![]() and $V\subset \mathbb {R}^{4}$
and $V\subset \mathbb {R}^{4}$![]() be open sets. Following Mather techniques of classification [Reference Mather10] we have that a proper $C^{\infty }$
be open sets. Following Mather techniques of classification [Reference Mather10] we have that a proper $C^{\infty }$![]() map $f\colon U\to V$
map $f\colon U\to V$![]() is stable if and only if $f$
is stable if and only if $f$![]() presents only the following phenomena: regular points, transverse double points, transverse triple points, singular points of cross-cap type ($f$
presents only the following phenomena: regular points, transverse double points, transverse triple points, singular points of cross-cap type ($f$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to $(x,y,z^{2},xz)$
-equivalent to $(x,y,z^{2},xz)$![]() ), transverse intersection of curves of cross-cap type with 3-planes of regular points and transverse quadruple points.
), transverse intersection of curves of cross-cap type with 3-planes of regular points and transverse quadruple points.
Assume now that $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() is finitely determined. Since $f$
is finitely determined. Since $f$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to its own $k$
-equivalent to its own $k$![]() -jet, for some $k$
-jet, for some $k$![]() , we can assume that $f$
, we can assume that $f$![]() is a real analytic map germ (in fact, polynomial). Moreover, by the Mather–Gaffney geometrical criterion [Reference Wall19], there is a representative $f\colon U\to V$
is a real analytic map germ (in fact, polynomial). Moreover, by the Mather–Gaffney geometrical criterion [Reference Wall19], there is a representative $f\colon U\to V$![]() , where $U\subset \mathbb {R}^{3}$
, where $U\subset \mathbb {R}^{3}$![]() and $V\subset \mathbb {R}^{4}$
and $V\subset \mathbb {R}^{4}$![]() are open neighbourhoods of the origin and such that
are open neighbourhoods of the origin and such that
(1) $f^{-1}(0)=\{0\}$
 ,
,(2) $f\colon U\to V$
 is proper,
is proper,(3) the restriction $f\colon U{\setminus} \{0\}\to V{\setminus} \{0\}$
 is a stable map.
is a stable map.
This means that $f$![]() has an isolated ‘instability’ at the origin. Moreover, if $f$
has an isolated ‘instability’ at the origin. Moreover, if $f$![]() is stable in $U{\setminus} \{0\}$
is stable in $U{\setminus} \{0\}$![]() , the quadruple points and the transverse intersections of cross-cap curves and 3-planes of regular points are isolated in $U{\setminus} \{0\}$
, the quadruple points and the transverse intersections of cross-cap curves and 3-planes of regular points are isolated in $U{\setminus} \{0\}$![]() . By the curve selection lemma, they are also isolated in $U$
. By the curve selection lemma, they are also isolated in $U$![]() . Hence, by shrinking the neighbourhood $U$
. Hence, by shrinking the neighbourhood $U$![]() if necessary, we can substitute condition (3) by the following stronger condition:
if necessary, we can substitute condition (3) by the following stronger condition:
(3.1) $f\colon U{\setminus} \{0\}\to V{\setminus} \{0\}$
 only presents regular points, transverse double points, transverse triple points and singular points of cross-cap type.
only presents regular points, transverse double points, transverse triple points and singular points of cross-cap type.
Definition 2.1 We say that $f\colon U\to V$![]() is a good representative if it satisfies conditions (1), (2) and (3.1) above. We say that $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$
is a good representative if it satisfies conditions (1), (2) and (3.1) above. We say that $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() has isolated instability if it admits a good representative.
has isolated instability if it admits a good representative.
We remark that any finitely determined map germ has isolated instability, but the converse is not true. For instance, the map germ $f(x,y,z)=(x,y,z^{2},z(x^{2}+y^{2})^{2})$![]() has isolated instability but its complexification has not isolated instability, so it is not finitely determined by the Mather–Gaffney criterion [Reference Wall19].
has isolated instability but its complexification has not isolated instability, so it is not finitely determined by the Mather–Gaffney criterion [Reference Wall19].
Let us define the double point space of a map germ.
Definition 2.2 Let $f\colon (\mathbb {R}^{3}, 0)\to (\mathbb {R}^{4},0)$![]() be a map germ. We define the set germ $D^{2}(f)$
be a map germ. We define the set germ $D^{2}(f)$![]() in $(\mathbb {R}^{3}\times \mathbb {R}^{3},0)$
in $(\mathbb {R}^{3}\times \mathbb {R}^{3},0)$![]() as the points $(x,y,z,x',y',z')$
as the points $(x,y,z,x',y',z')$![]() such that either $f(x,y,z)=f(x',y',z')$
such that either $f(x,y,z)=f(x',y',z')$![]() and $(x,y,z)\neq (x',y',z')$
and $(x,y,z)\neq (x',y',z')$![]() or $f$
or $f$![]() is not immersive at $(x,y,z)$
is not immersive at $(x,y,z)$![]() and $(x',y',z')=(x,y,z)$
and $(x',y',z')=(x,y,z)$![]() .
.
The double point space is defined as $D(f) = p_1(D^{2}(f)) \subset (\mathbb {R}^{3},0)$![]() , where $p_1\colon \mathbb {R}^{3}\times \mathbb {R}^{3}\to \mathbb {R}^{3}$
, where $p_1\colon \mathbb {R}^{3}\times \mathbb {R}^{3}\to \mathbb {R}^{3}$![]() is the canonical projection. In other words, $D(f)$
is the canonical projection. In other words, $D(f)$![]() is given by the points $(x,y,z)$
is given by the points $(x,y,z)$![]() such that either $f^{-1}(f(x,y,z))\neq \{(x,y,z)\}$
such that either $f^{-1}(f(x,y,z))\neq \{(x,y,z)\}$![]() or $f$
or $f$![]() is not immersive at $(x,y,z)$
is not immersive at $(x,y,z)$![]() .
.
To finish this section we review the cone structure of a map germ $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() with isolated instability, following the arguments of Fukuda in [Reference Fukuda6]. Let us fix some notation:
with isolated instability, following the arguments of Fukuda in [Reference Fukuda6]. Let us fix some notation:
Given a map germ $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() we take a representative $f:U\to V$
we take a representative $f:U\to V$![]() and we also set:
and we also set:
Theorem 2.3 Let $f\colon U\to V$![]() be a good representative of a map germ $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$
be a good representative of a map germ $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() with isolated instability. Then there is $\epsilon _0>0$
with isolated instability. Then there is $\epsilon _0>0$![]() such that for any $\epsilon$
such that for any $\epsilon$![]() with $0<\epsilon \le \epsilon _0$
with $0<\epsilon \le \epsilon _0$![]() we have:
we have:
(1) $\tilde S_\epsilon ^{2}$
 is diffeomorphic to $S^{2}$
is diffeomorphic to $S^{2}$ ,
,(2) $f|_{\tilde S_\epsilon ^{2}}\colon \tilde S_\epsilon ^{2}\to S_\epsilon ^{3}$
 is stable and its $\mathcal {A}$
is stable and its $\mathcal {A}$ -class is independent of $\epsilon$
-class is independent of $\epsilon$ .
.(3) $f|_{\tilde D_\epsilon ^{3}}\colon \tilde D_\epsilon ^{3}\to D_\epsilon ^{4}$
 is topologically equivalent to the cone on $f|_{\tilde S_\epsilon ^{2}}$
is topologically equivalent to the cone on $f|_{\tilde S_\epsilon ^{2}}$ .
.
Definition 2.4 Let $f\colon U\to V$![]() be a good representative of a map germ $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$
be a good representative of a map germ $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() with isolated instability. We call the stable map $f|_{\tilde S_\epsilon ^{2}}\colon \tilde S_\epsilon ^{2}\to S_\epsilon ^{3}$
with isolated instability. We call the stable map $f|_{\tilde S_\epsilon ^{2}}\colon \tilde S_\epsilon ^{2}\to S_\epsilon ^{3}$![]() the link of $f$
the link of $f$![]() .
.
It follows from theorem 2.3 that the link is a stable map $\gamma \colon S^{2}\to S^{3}$![]() , that is, it only presents regular points, transverse double point curves, singular points of cross-cap type and transverse triple points. Moreover, the link is well defined up to $\mathcal {A}$
, that is, it only presents regular points, transverse double point curves, singular points of cross-cap type and transverse triple points. Moreover, the link is well defined up to $\mathcal {A}$![]() -equivalence and that the map germ $f$
-equivalence and that the map germ $f$![]() is topologically equivalent to the cone on its link. In particular, we have the following immediate consequence, which implies that the topological classification of map germs from $(\mathbb {R}^{3},0)$
is topologically equivalent to the cone on its link. In particular, we have the following immediate consequence, which implies that the topological classification of map germs from $(\mathbb {R}^{3},0)$![]() to $(\mathbb {R}^{4},0)$
to $(\mathbb {R}^{4},0)$![]() with isolated instability can be reduced to the topological classification of their associated links.
with isolated instability can be reduced to the topological classification of their associated links.
Corollary 2.5 Let $f, g\colon (\mathbb {R}^{3}, 0) \rightarrow (\mathbb {R}^{4}, 0)$![]() be two map germs with isolated instability whose associated links are topologically equivalent. Then $f$
be two map germs with isolated instability whose associated links are topologically equivalent. Then $f$![]() and $g$
and $g$![]() are topologically equivalent.
are topologically equivalent.
We will see that the converse of this corollary is also true at the end of §4, if we assume that $f$![]() and $g$
and $g$![]() are of fold type.
are of fold type.
3. Map germs of fold type
The aim of this section is to obtain a prenormal form for map germs $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() that are of fold type, that is, they belong to the Thom–Boardman class $\Sigma ^{1,0}$
that are of fold type, that is, they belong to the Thom–Boardman class $\Sigma ^{1,0}$![]() . To do this, we follow Mond's arguments in [Reference Mond13] for map germs $(\mathbb {R}^{2},0)\to (\mathbb {R}^{3},0)$
. To do this, we follow Mond's arguments in [Reference Mond13] for map germs $(\mathbb {R}^{2},0)\to (\mathbb {R}^{3},0)$![]() . The first step is to calculate the different $\mathcal {A}^{2}$
. The first step is to calculate the different $\mathcal {A}^{2}$![]() -classes that we have inside the set of germs of corank 1.
-classes that we have inside the set of germs of corank 1.
Lemma 3.1 Let $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() be a corank 1 map germ. Then, its 2-jet $j^{2}f(0)$
be a corank 1 map germ. Then, its 2-jet $j^{2}f(0)$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to either $(x,y,z^{2},xz), (x,y,xz,yz), (x,y,z^{2},0),$
-equivalent to either $(x,y,z^{2},xz), (x,y,xz,yz), (x,y,z^{2},0),$![]() $(x,y,xz,0)$
$(x,y,xz,0)$![]() or $(x,y,0,0).$
or $(x,y,0,0).$![]()
Proof. Since by hypothesis we are working in corank 1, by coordinate changes in the source and target, we can assume that
for some homogeneous polynomials $p(x,y,z),q(x,y,z)$![]() of degree 2. By using another coordinate change in the target we can remove in $j^{2}f(0)$
of degree 2. By using another coordinate change in the target we can remove in $j^{2}f(0)$![]() all the terms that only depend on the variables $x, y$
all the terms that only depend on the variables $x, y$![]() and thus we obtain that $j^{2}f(0)$
and thus we obtain that $j^{2}f(0)$![]() is equivalent to
is equivalent to
Let $\alpha =\left(\!\begin{smallmatrix}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3\end{smallmatrix}\!\right)$![]() and we suppose that $\operatorname {rank}(\alpha )=2$
and we suppose that $\operatorname {rank}(\alpha )=2$![]() .
.
We consider different cases.
• If $(a_1,b_1)\neq (0,0)$
 , without loss of generality we can suppose that $a_1\neq 0$
, without loss of generality we can suppose that $a_1\neq 0$ .
.First of all, we make the coordinate changes in the target
\[ \begin{cases}\overline{X}=X \\ \overline{Y}=Y \\ \overline{Z}=Z\\ \overline{T}=T - \frac{b_1}{a_1}Z\end{cases} \]and we get that $j^{2}f(0)\sim (x,y,a_1z^{2}+a_2xz+a_3yz, \overline {b_2}xz+\overline {b_3}yz).$

With a change in the source
\[ \begin{cases}x=\overline{x}\\ y=\overline{y}\\ z=\overline{z}-\frac{a_2}{2a_1}\overline{x}-\frac{a_3}{2a_1}\overline{y}\end{cases} \]we get that $j^{2}f(0)\sim (x,y,z^{2},\overline {b_2}xz+\overline {b_3}yz).$

Since $\operatorname {rank}(\alpha )=2$
 , we can suppose that $\overline {b_2}\neq 0$
, we can suppose that $\overline {b_2}\neq 0$ and making in first place a change in the source
\[ \begin{cases} x=\overline{x} - \frac{\overline{b_3}}{\overline{b_2}}\overline{y}\\ y=\overline{y}\\ z=\overline{z}\end{cases} \]and after that a change in the target
and making in first place a change in the source
\[ \begin{cases} x=\overline{x} - \frac{\overline{b_3}}{\overline{b_2}}\overline{y}\\ y=\overline{y}\\ z=\overline{z}\end{cases} \]and after that a change in the target \[ \begin{cases} \overline{X}=X +\frac{\overline{b_3}}{\overline{b_2}}Y\\ \overline{Y}=Y\\ \overline{Z}=Z\\ \overline{T}=T\end{cases} \]we get that $j^{2}f(0)\sim (x,y,z^{2},xz).$
\[ \begin{cases} \overline{X}=X +\frac{\overline{b_3}}{\overline{b_2}}Y\\ \overline{Y}=Y\\ \overline{Z}=Z\\ \overline{T}=T\end{cases} \]we get that $j^{2}f(0)\sim (x,y,z^{2},xz).$

• If $(a_1,b_1)= (0,0)$
 using the fact that $\operatorname {rank}(\alpha )=2$
using the fact that $\operatorname {rank}(\alpha )=2$ and applying suitable change of coordinates we get that $j^{2}f(0)\sim (x,y,xz,yz)$
and applying suitable change of coordinates we get that $j^{2}f(0)\sim (x,y,xz,yz)$ .
.
If $\operatorname {rank}(\alpha )=1$![]() we have that $j^{2}f(0)\sim (x,y,a_1z^{2}+a_2xz+a_3yz,0)$
we have that $j^{2}f(0)\sim (x,y,a_1z^{2}+a_2xz+a_3yz,0)$![]() , obtaining, following an analogous procedure to the previous case the $\mathcal {A}^{2}$
, obtaining, following an analogous procedure to the previous case the $\mathcal {A}^{2}$![]() -orbits $(x,y,z^{2},0)$
-orbits $(x,y,z^{2},0)$![]() and $(x,y,xz,0)$
and $(x,y,xz,0)$![]() .
.
Finally, if $\operatorname {rank}(\alpha )=0$![]() we get that $j^{2}f(0)\sim (x,y,0,0).$
we get that $j^{2}f(0)\sim (x,y,0,0).$![]()
The following result gives us the $\mathcal {A}^{2}$![]() -classes of type $\Sigma ^{1,0}$
-classes of type $\Sigma ^{1,0}$![]() . We denote by $\mathscr E_3$
. We denote by $\mathscr E_3$![]() the local ring of smooth function germs $(\mathbb {R}^{3},0)\to \mathbb {R}$
the local ring of smooth function germs $(\mathbb {R}^{3},0)\to \mathbb {R}$![]() , with maximal ideal $\mathfrak m_3$
, with maximal ideal $\mathfrak m_3$![]() .
.
Lemma 3.2 The $\mathcal {A}^{2}$![]() -classes $(x,y,z^{2},0)$
-classes $(x,y,z^{2},0)$![]() and $(x,y,z^{2},xz)$
and $(x,y,z^{2},xz)$![]() are Thom–Boardman type $\Sigma ^{1,0}$
are Thom–Boardman type $\Sigma ^{1,0}$![]() . The rest $\mathcal {A}^{2}$
. The rest $\mathcal {A}^{2}$![]() -classes in lemma 3.1 are not.
-classes in lemma 3.1 are not.
Proof. Since we are considering the corank 1 case, all $\mathcal {A}^{2}$![]() -classes are of Thom–Boardman type $\Sigma ^{1}$
-classes are of Thom–Boardman type $\Sigma ^{1}$![]() . If we compute the Jacobian matrix of each class, in the case of $(x,y,z^{2},xz), (x,y,z^{2},0)$
. If we compute the Jacobian matrix of each class, in the case of $(x,y,z^{2},xz), (x,y,z^{2},0)$![]() they have the $3\times 3$
they have the $3\times 3$![]() minor $z$
minor $z$![]() , that is, if we denote by $I$
, that is, if we denote by $I$![]() the ideal in $\mathscr E_3$
the ideal in $\mathscr E_3$![]() generated by the components of $j^{2}f(0)$
generated by the components of $j^{2}f(0)$![]() and the minors of the Jacobian matrix, we have in this case that $I= \langle x,y,z \rangle$
and the minors of the Jacobian matrix, we have in this case that $I= \langle x,y,z \rangle$![]() . Therefore, $\operatorname {dim}_{\mathbb {R}}I/\mathfrak m_3 I =3$
. Therefore, $\operatorname {dim}_{\mathbb {R}}I/\mathfrak m_3 I =3$![]() and, as a consequence, all of them are of Thom–Boardman type $\Sigma ^{1,0}.$
and, as a consequence, all of them are of Thom–Boardman type $\Sigma ^{1,0}.$![]()
Otherwise, if we consider the rest of the classes, $I$![]() has terms in $z$
has terms in $z$![]() of multiplicity greater or equal than two. Thus, $\operatorname {dim}_{\mathbb {R}}I/\mathfrak m_3 I =2$
of multiplicity greater or equal than two. Thus, $\operatorname {dim}_{\mathbb {R}}I/\mathfrak m_3 I =2$![]() and they belong to the Thom–Boardman class $\Sigma ^{1,1}$
and they belong to the Thom–Boardman class $\Sigma ^{1,1}$![]() .
.
Combining lemmas 3.1 and 3.2 we can state the main result of this section.
Lemma 3.3 Let $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() be a map germ with Thom–Boardman type $\Sigma ^{1,0}$
be a map germ with Thom–Boardman type $\Sigma ^{1,0}$![]() . Then, $f$
. Then, $f$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to a map germ of the form
-equivalent to a map germ of the form
where $p\in \mathfrak m_3$![]() .
.
Proof. Since $f$![]() has Thom–Boardman type $\Sigma ^{1,0}$
has Thom–Boardman type $\Sigma ^{1,0}$![]() , by lemma 3.2 its 2-jet is $\mathcal {A}$
, by lemma 3.2 its 2-jet is $\mathcal {A}$![]() -equivalent to $(x,y,z^{2},xz)$
-equivalent to $(x,y,z^{2},xz)$![]() or $(x,y,z^{2},0)$
or $(x,y,z^{2},0)$![]() . Therefore,
. Therefore,
with $P_1\in \mathfrak {m}_3^{3}$![]() , $P_2\in \mathfrak {m}_3^{2}.$
, $P_2\in \mathfrak {m}_3^{2}.$![]()
Since $(x,y,z^{2})$![]() is 2-determined, $f$
is 2-determined, $f$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to $(x,y,z^{2}, A(x,y,z)),$
-equivalent to $(x,y,z^{2}, A(x,y,z)),$![]() for some $A\in \mathfrak {m}_3^{2}$
for some $A\in \mathfrak {m}_3^{2}$![]() . Applying the Malgrange Preparation theorem [Reference Mond and Nuño-Ballesteros14], we can write
. Applying the Malgrange Preparation theorem [Reference Mond and Nuño-Ballesteros14], we can write
for some $B,C\in \mathscr E_3$![]() . Taking the coordinate change in the target
. Taking the coordinate change in the target

we get the requested result.
Remark 3.4 Let $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() be a map germ of fold type. By lemma 3.3, after applying a suitable change of coordinates, $f(x,y,z) = (x, y, z^{2}, zp(x,y,z^{2})$
be a map germ of fold type. By lemma 3.3, after applying a suitable change of coordinates, $f(x,y,z) = (x, y, z^{2}, zp(x,y,z^{2})$![]() . This implies that:
. This implies that:
(1) $f$
 has no triple points,
has no triple points,(2) the double point space $D(f)$
 is given by the equation $p(x,y,z^{2})=0$
is given by the equation $p(x,y,z^{2})=0$ , so is symmetric with respect to the plane $z=0$
, so is symmetric with respect to the plane $z=0$ ,
,(3) the image of $f$
 is contained in the half-space $Z\ge 0$
is contained in the half-space $Z\ge 0$ and is symmetric with respect to the hyperplane $T=0$
and is symmetric with respect to the hyperplane $T=0$ ,
,(4) the image of $f$
 intersects the hyperplane $T=0$
intersects the hyperplane $T=0$ only at the double points.
only at the double points.
4. Mosaics and dual graphs
In this section we introduce the concept of a mosaic in the 2-disc $D^{2}$![]() and we associate it with a graph $\Gamma$
and we associate it with a graph $\Gamma$![]() that codifies all its topological information. First of all, we define what a mosaic is.
that codifies all its topological information. First of all, we define what a mosaic is.
Definition 4.1 We call a mosaic in $D^{2}$![]() to a pair $(D^{2},K)$
to a pair $(D^{2},K)$![]() where $K\subset D^{2}$
where $K\subset D^{2}$![]() is a closed 1-dimensional submanifold with boundary such that $\partial K=K\cap \partial D^{2}$
is a closed 1-dimensional submanifold with boundary such that $\partial K=K\cap \partial D^{2}$![]() . We will say that two mosaics $(D^{2},K)$
. We will say that two mosaics $(D^{2},K)$![]() and $(D^{2},K')$
and $(D^{2},K')$![]() are equivalent if there is a homeomorphism $\phi \colon D^{2}\to D^{2}$
are equivalent if there is a homeomorphism $\phi \colon D^{2}\to D^{2}$![]() such that $\phi (K)=K'$
such that $\phi (K)=K'$![]() .
.
For a mosaic $(D^{2},K)$![]() , descompose $K=C_1\cup \cdots \cup C_s\cup D_1\cup \cdots \cup D_t$
, descompose $K=C_1\cup \cdots \cup C_s\cup D_1\cup \cdots \cup D_t$![]() into connected components, where $C_i$
into connected components, where $C_i$![]() are simple arcs whose ends are the only boundary points of $D^{2}$
are simple arcs whose ends are the only boundary points of $D^{2}$![]() and $D_j$
and $D_j$![]() are simple closed curves in the interior of $D^{2}$
are simple closed curves in the interior of $D^{2}$![]() . In figure 1 we have an example of a mosaic.
. In figure 1 we have an example of a mosaic.
Definition 4.2 Let $(D^{2},K)$![]() be a mosaic. We can associate a graph $\Gamma =(V, E)$
be a mosaic. We can associate a graph $\Gamma =(V, E)$![]() such that each vertex $v_i\in V$
such that each vertex $v_i\in V$![]() corresponds to a connected component of $D^{2}{\setminus} K$
corresponds to a connected component of $D^{2}{\setminus} K$![]() and $v_iv_j\in E$
and $v_iv_j\in E$![]() if and only if the respective connected components are separated from each other by a connected component of $K$
if and only if the respective connected components are separated from each other by a connected component of $K$![]() . We use $\ast$
. We use $\ast$![]() to denote the vertices that correspond to a connected component with boundary points in its closure and $\bullet$
to denote the vertices that correspond to a connected component with boundary points in its closure and $\bullet$![]() to the others. We call $\Gamma$
to the others. We call $\Gamma$![]() the dual graph of the mosaic $(D^{2}, K)$
the dual graph of the mosaic $(D^{2}, K)$![]() .
.

Figure 1. Example of a mosaic.
Example 4.3 We give some examples of dual graphs of mosaics:
(1) Let $(D^{2},K)$
 be a mosaic such that $K=\emptyset$
be a mosaic such that $K=\emptyset$ . Therefore, its dual graph has only one vertex of type $\ast$
. Therefore, its dual graph has only one vertex of type $\ast$ (figure 2)
(figure 2)(2) Let $(D^{2},K)$
 be a mosaic such that $K=C$
be a mosaic such that $K=C$ a simple arc. Therefore, its dual graph has two vertices of type $\ast$
a simple arc. Therefore, its dual graph has two vertices of type $\ast$ (figure 3)
(figure 3)(3) Let $(D^{2},K)$
 be a mosaic such that $K=D$
be a mosaic such that $K=D$ a simple closed curve. Therefore, its dual graph has two vertices, one of type $\ast$
a simple closed curve. Therefore, its dual graph has two vertices, one of type $\ast$ and one of type $\bullet$
and one of type $\bullet$ (figure 4)
(figure 4)(4) Let $(D^{2},K)$
 be the mosaic of figure 1. Therefore, its dual graph has ten vertices, six of type $\ast$
be the mosaic of figure 1. Therefore, its dual graph has ten vertices, six of type $\ast$ and four of type $\bullet$
and four of type $\bullet$ , whose configuration is the following (figure 5):
, whose configuration is the following (figure 5):
Lemma 4.4 The dual graph $\Gamma$![]() of a mosaic $(D^{2},K)$
of a mosaic $(D^{2},K)$![]() has a final vertex, that is, a vertex of degree one. Moreover, if $\Gamma$
has a final vertex, that is, a vertex of degree one. Moreover, if $\Gamma$![]() has vertices of type $\bullet$
has vertices of type $\bullet$![]() , at least one of them must be final.
, at least one of them must be final.
Proof. Let $\Gamma$![]() be the dual graph of a mosaic $(D^{2},K)$
be the dual graph of a mosaic $(D^{2},K)$![]() . Let us see first that $\Gamma$
. Let us see first that $\Gamma$![]() always have a final vertex. Since any vertex of $\Gamma$
always have a final vertex. Since any vertex of $\Gamma$![]() corresponds to a connected component of $D^{2}{\setminus} K$
corresponds to a connected component of $D^{2}{\setminus} K$![]() , this is equivalent to see that we can find a connected component that does not contain other connected component. But this is easy to prove applying Jordan's Curve Theorem. If we start drawing any of the connected components of $K$
, this is equivalent to see that we can find a connected component that does not contain other connected component. But this is easy to prove applying Jordan's Curve Theorem. If we start drawing any of the connected components of $K$![]() , it divides $D^{2}$
, it divides $D^{2}$![]() in 2 parts. If we choose one of them (the interior one in the case of having a closed curve), we again have a disc and we can repeat the procedure, that will finish after a finite number of steps, by the finiteness of the number of connected components of $K$
in 2 parts. If we choose one of them (the interior one in the case of having a closed curve), we again have a disc and we can repeat the procedure, that will finish after a finite number of steps, by the finiteness of the number of connected components of $K$![]() , obtaining a final vertex.
, obtaining a final vertex.

Figure 2. Dual graph of the empty mosaic.

Figure 3. Dual graph of a mosaic with a simple arc.

Figure 4. Dual graph of a mosaic with a simple closed curve.

Figure 5. Dual graph of the mosaic of Figure 1.
If $\Gamma$![]() has at least a vertex of type $\bullet$
has at least a vertex of type $\bullet$![]() , then $K$
, then $K$![]() has at least a connected component which is a closed curve. We take the interior of such a closed curve in $D^{2}$
has at least a connected component which is a closed curve. We take the interior of such a closed curve in $D^{2}$![]() and the same argument as above implies that we have at least a final vertex of type $\bullet$
and the same argument as above implies that we have at least a final vertex of type $\bullet$![]() .
.
The following result gives us the answer of when a graph $\Gamma$![]() will be the dual graph of a mosaic $(D^{2},K)$
will be the dual graph of a mosaic $(D^{2},K)$![]() .
.
Theorem 4.5 Let $\Gamma =(V,E)$![]() be a graph with vertices of type $\ast$
be a graph with vertices of type $\ast$![]() and $\bullet$
and $\bullet$![]() . Then $\Gamma$
. Then $\Gamma$![]() is the dual graph of a mosaic $(D^{2},K)$
is the dual graph of a mosaic $(D^{2},K)$![]() if and only if:
if and only if:
(1) $\Gamma$
 is a tree,
is a tree,(2) $\Gamma$
 has at least a vertex of type $\ast$
has at least a vertex of type $\ast$ and if it contains two or more, they are connected by a path that does not contain vertices of type $\bullet$
and if it contains two or more, they are connected by a path that does not contain vertices of type $\bullet$ .
.
Proof. Let us suppose that $\Gamma$![]() is the dual graph of a mosaic $(D^{2},K)$
is the dual graph of a mosaic $(D^{2},K)$![]() . To prove $(1)$
. To prove $(1)$![]() we use the fact that a connected graph $\Gamma$
we use the fact that a connected graph $\Gamma$![]() is a tree if and only if its Euler characteristic is $\chi (\Gamma )=1$
is a tree if and only if its Euler characteristic is $\chi (\Gamma )=1$![]() . We prove it by induction on the number of vertices of $\Gamma$
. We prove it by induction on the number of vertices of $\Gamma$![]() . For dual graphs with 1 and 2 vertices it is clear from example 4.3. Let us suppose this is true for a dual graph with $v-1$
. For dual graphs with 1 and 2 vertices it is clear from example 4.3. Let us suppose this is true for a dual graph with $v-1$![]() vertices (and $v-2$
vertices (and $v-2$![]() edges by the fact of having Euler characteristic equal to 1). Assume $\Gamma$
edges by the fact of having Euler characteristic equal to 1). Assume $\Gamma$![]() has $v$
has $v$![]() vertices. By lemma 4.4, $\Gamma$
vertices. By lemma 4.4, $\Gamma$![]() has a final vertex $v_i$
has a final vertex $v_i$![]() connected to another vertex $v_j$
connected to another vertex $v_j$![]() . We can eliminate the vertex $v_i$
. We can eliminate the vertex $v_i$![]() , obtaining a graph $\Gamma '$
, obtaining a graph $\Gamma '$![]() with $v-1$
with $v-1$![]() vertices. Moreover, $\Gamma '$
vertices. Moreover, $\Gamma '$![]() is the dual graph of the mosaic $(D^{2},K')$
is the dual graph of the mosaic $(D^{2},K')$![]() , where $K'$
, where $K'$![]() is obtained from $K$
is obtained from $K$![]() by elimination of the connected component corresponding to the edge $v_iv_j$
by elimination of the connected component corresponding to the edge $v_iv_j$![]() . By induction, $\chi (\Gamma ')=1$
. By induction, $\chi (\Gamma ')=1$![]() and hence $\chi (\Gamma )= (v-1)+1-((v-2)+1)= 1$
and hence $\chi (\Gamma )= (v-1)+1-((v-2)+1)= 1$![]() , since we are adding a final vertex.
, since we are adding a final vertex.
We use again induction on the number of vertices to prove $(2)$![]() . For dual graphs with 1 and 2 vertices it is clear from example 4.3. Let us suppose this is true for a dual graph with $v-1$
. For dual graphs with 1 and 2 vertices it is clear from example 4.3. Let us suppose this is true for a dual graph with $v-1$![]() vertices. If we consider a graph with $v$
vertices. If we consider a graph with $v$![]() vertice and with a vertice of type $\bullet$
vertice and with a vertice of type $\bullet$![]() in the path that connects two vertices of type $\ast$
in the path that connects two vertices of type $\ast$![]() (and as a consequence not final), if we eliminate a final vertex of type $\bullet$
(and as a consequence not final), if we eliminate a final vertex of type $\bullet$![]() we have the same situation but in a graph with $v-1$
we have the same situation but in a graph with $v-1$![]() vertices, arriving to a contradiction.
vertices, arriving to a contradiction.
To see the converse we prove that given a graph $\Gamma$![]() that verifies $(1)$
that verifies $(1)$![]() and $(2)$
and $(2)$![]() we can build a mosaic $(D^{2},K)$
we can build a mosaic $(D^{2},K)$![]() whose dual graph is $\Gamma$
whose dual graph is $\Gamma$![]() . Again we do it by induction on the number of vertices of $\Gamma$
. Again we do it by induction on the number of vertices of $\Gamma$![]() . Let us suppose first that $\Gamma$
. Let us suppose first that $\Gamma$![]() only has vertices of type $\ast$
only has vertices of type $\ast$![]() . For 1, 2 and 3 vertices this is true from example 4.3. If we suppose it is true for $v-1$
. For 1, 2 and 3 vertices this is true from example 4.3. If we suppose it is true for $v-1$![]() vertices and we consider a graph $\Gamma$
vertices and we consider a graph $\Gamma$![]() with $v$
with $v$![]() vertices, by the fact of having a tree [condition $(1)$
vertices, by the fact of having a tree [condition $(1)$![]() ] we know that $\Gamma$
] we know that $\Gamma$![]() has a final vertex $v_i$
has a final vertex $v_i$![]() connected to another vertex $v_j$
connected to another vertex $v_j$![]() . We eliminate $v_i$
. We eliminate $v_i$![]() and obtain a graph $\Gamma '$
and obtain a graph $\Gamma '$![]() with $v-1$
with $v-1$![]() vertices that also satisfies conditions $(1)$
vertices that also satisfies conditions $(1)$![]() and $(2)$
and $(2)$![]() . By induction hypothesis, $\Gamma '$
. By induction hypothesis, $\Gamma '$![]() is the dual graph of a mosaic $(D^{2},K)$
is the dual graph of a mosaic $(D^{2},K)$![]() . We can get the mosaic whose associated dual graph is $\Gamma$
. We can get the mosaic whose associated dual graph is $\Gamma$![]() just by adding a new arc $C_i$
just by adding a new arc $C_i$![]() to $K$
to $K$![]() in the connected component corresponding to $v_j$
in the connected component corresponding to $v_j$![]() .
.
We consider now the general case where we may have also vertices of type $\bullet$![]() . We use induction on the number of vertices of type $\bullet$
. We use induction on the number of vertices of type $\bullet$![]() . For 0 vertices it is true by the previous case. Assume it is true for $v-1$
. For 0 vertices it is true by the previous case. Assume it is true for $v-1$![]() vertices and suppose $\Gamma$
vertices and suppose $\Gamma$![]() has $v$
has $v$![]() vertices. By condition $(2)$
vertices. By condition $(2)$![]() , $\Gamma$
, $\Gamma$![]() has at least a final vertex $v_i$
has at least a final vertex $v_i$![]() of type $\bullet$
of type $\bullet$![]() connected to another vertex $v_j$
connected to another vertex $v_j$![]() . We can eliminate $v_i$
. We can eliminate $v_i$![]() and repeat the same procedure used in the previous case. We obtain that $\Gamma$
and repeat the same procedure used in the previous case. We obtain that $\Gamma$![]() is the dual graph of a mosaic $(D^{2},K)$
is the dual graph of a mosaic $(D^{2},K)$![]() .
.
Remark 4.6 Since the dual graph $\Gamma$![]() of a mosaic $(D^{2},K)$
of a mosaic $(D^{2},K)$![]() is a tree, we call it the dual tree of $(D^{2},K)$
is a tree, we call it the dual tree of $(D^{2},K)$![]() . By conditions $(1)$
. By conditions $(1)$![]() and $(2)$
and $(2)$![]() of theorem 4.5 we have that the subgraph of $\Gamma$
of theorem 4.5 we have that the subgraph of $\Gamma$![]() given by all the vertices of type $\ast$
given by all the vertices of type $\ast$![]() is also a tree, which can be seen as the ‘trunk’ of $\Gamma$
is also a tree, which can be seen as the ‘trunk’ of $\Gamma$![]() . Each connected component of the subgraph of $\Gamma$
. Each connected component of the subgraph of $\Gamma$![]() given by all the vertices of type $\bullet$
given by all the vertices of type $\bullet$![]() is also a tree and is connected at most to one vertex of type $\ast$
is also a tree and is connected at most to one vertex of type $\ast$![]() . These connected components can be seen as the ‘branches’ of $\Gamma$
. These connected components can be seen as the ‘branches’ of $\Gamma$![]() .
.
It is natural to introduce the following notion of equivalence of dual trees of mosaics.
Definition 4.7 We say that two dual trees $\Gamma =(V,E)$![]() and $\Gamma '=(V',E')$
and $\Gamma '=(V',E')$![]() are equivalent if they are isomorphic and, moreover, the bijection $\alpha \colon V\to V'$
are equivalent if they are isomorphic and, moreover, the bijection $\alpha \colon V\to V'$![]() sends vertices of type $\ast$
sends vertices of type $\ast$![]() (resp. $\bullet$
(resp. $\bullet$![]() ) to vertices of type $\ast$
) to vertices of type $\ast$![]() (resp. $\bullet$
(resp. $\bullet$![]() ).
).
Now, we can state and prove the final result of this section.
Theorem 4.8 Two mosaics $(D^{2},K)$![]() and $(D^{2},K')$
and $(D^{2},K')$![]() are equivalent if and only if their associated dual trees $\Gamma =(V,E)$
are equivalent if and only if their associated dual trees $\Gamma =(V,E)$![]() and $\Gamma '= (V', E')$
and $\Gamma '= (V', E')$![]() are equivalent.
are equivalent.
Proof. If $(D^{2},K)$![]() and $(D^{2},K')$
and $(D^{2},K')$![]() are equivalent, there is a homeomorphism $\phi \colon D^{2}\to D^{2}$
are equivalent, there is a homeomorphism $\phi \colon D^{2}\to D^{2}$![]() such that $\phi (K)=K'$
such that $\phi (K)=K'$![]() and the relative position of their connected components is the same. This induces a bijection $\alpha \colon V\to V'$
and the relative position of their connected components is the same. This induces a bijection $\alpha \colon V\to V'$![]() that sends vertices of type $\ast$
that sends vertices of type $\ast$![]() (resp. $\bullet$
(resp. $\bullet$![]() ) to vertices of type $\ast$
) to vertices of type $\ast$![]() (resp. $\bullet$
(resp. $\bullet$![]() ) and $v_iv_j\in E$
) and $v_iv_j\in E$![]() if and only if $\alpha (v_i)\alpha (v_j)\in E'$
if and only if $\alpha (v_i)\alpha (v_j)\in E'$![]() . Therefore $\Gamma$
. Therefore $\Gamma$![]() and $\Gamma '$
and $\Gamma '$![]() are equivalent.
are equivalent.
We prove the converse by induction on the number of vertices of $\Gamma$![]() . For 1 vertex, $K=K'=\emptyset$
. For 1 vertex, $K=K'=\emptyset$![]() and both mosaics $(D^{2},K)$
and both mosaics $(D^{2},K)$![]() and $(D^{2},K')$
and $(D^{2},K')$![]() are equal. If the result is true for dual trees with $v-1$
are equal. If the result is true for dual trees with $v-1$![]() vertices, we consider two dual trees with $v$
vertices, we consider two dual trees with $v$![]() vertices $\Gamma$
vertices $\Gamma$![]() and $\Gamma '$
and $\Gamma '$![]() that are equivalent. We eliminate a final vertex $v_i$
that are equivalent. We eliminate a final vertex $v_i$![]() of $\Gamma$
of $\Gamma$![]() and its corresponding in $\Gamma ',$
and its corresponding in $\Gamma ',$![]() $v'_i$
$v'_i$![]() , obtaining two new graphs $\Gamma _1$
, obtaining two new graphs $\Gamma _1$![]() and $\Gamma _1'$
and $\Gamma _1'$![]() of $v-1$
of $v-1$![]() vertices that are equivalent. By induction hypothesis, their corresponding mosaics, $(D^{2},K_1)$
vertices that are equivalent. By induction hypothesis, their corresponding mosaics, $(D^{2},K_1)$![]() and $(D^{2},K'_1)$
and $(D^{2},K'_1)$![]() are equivalent. If we add to $K_1$
are equivalent. If we add to $K_1$![]() and $K_1'$
and $K_1'$![]() the connected component that we have eliminated associated to the vertices $v_i$
the connected component that we have eliminated associated to the vertices $v_i$![]() and $v'_i$
and $v'_i$![]() respectively, we obtain two equivalent mosaics, which are also equivalent to $(D^{2},K)$
respectively, we obtain two equivalent mosaics, which are also equivalent to $(D^{2},K)$![]() and $(D^{2},K')$
and $(D^{2},K')$![]() .
.
5. The dual tree of a stable map
In this section we construct a complete topological invariant for map germs $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() of fold type. We first introduce the notion of folded stable map, which is motivated by remark 3.4.
of fold type. We first introduce the notion of folded stable map, which is motivated by remark 3.4.
Let us consider the 2-sphere
and the 3-sphere
Definition 5.1 Let $\gamma \colon S^{2}\to S^{3}$![]() be a stable map. We say that $\gamma$
be a stable map. We say that $\gamma$![]() is folded if it satisfies the three following conditions:
is folded if it satisfies the three following conditions:
• $\gamma$
 has no triple points,
has no triple points,• $D(\gamma )$
 is symmetric with respect to the plane $z=0$
is symmetric with respect to the plane $z=0$ ,
,• $\gamma (S^{2})$
 is contained in the hemisphere $Z\geq 0$
is contained in the hemisphere $Z\geq 0$ and is symmetric with respect to the meridian $T=0$
and is symmetric with respect to the meridian $T=0$ ,
,• $\gamma (S^{2})$
 intersects $T=0$
intersects $T=0$ only at the double points.
only at the double points.
This implies that $\gamma (D(\gamma ))\subset \{T=0,Z\geq 0\}\cap S^{3}=S^{2}_+$![]() , which is diffeomorphic to $D^{2}$
, which is diffeomorphic to $D^{2}$![]() .
.
Definition 5.2 Let $\gamma \colon S^{2}\to S^{3}$![]() be a folded stable map. Therefore, $\gamma (D(\gamma ))\subset S^{2}_+$
be a folded stable map. Therefore, $\gamma (D(\gamma ))\subset S^{2}_+$![]() and it is a disjoint union of simple arcs $C_1\sqcup C_2\sqcup \cdots \sqcup C_k\sqcup D_1\sqcup \cdots \sqcup D_j$
and it is a disjoint union of simple arcs $C_1\sqcup C_2\sqcup \cdots \sqcup C_k\sqcup D_1\sqcup \cdots \sqcup D_j$![]() , where $C_i$
, where $C_i$![]() is a simple curve that starts and ends in the border of $S^{2}_+$
is a simple curve that starts and ends in the border of $S^{2}_+$![]() and $D_i$
and $D_i$![]() is a simple closed curve. This implies that $(S^{2}_+,\gamma (D(\gamma )))$
is a simple closed curve. This implies that $(S^{2}_+,\gamma (D(\gamma )))$![]() is a mosaic.
is a mosaic.
We call the dual tree of $\gamma$![]() to the dual tree of the mosaic $(S^{2}_+, \gamma (D(\gamma )))$
to the dual tree of the mosaic $(S^{2}_+, \gamma (D(\gamma )))$![]() .
.
Remark 5.3 If $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() is a map germ of fold type, then its associated link $f|_{\widetilde {S}_{\epsilon }^{2}}\colon \widetilde {S}_{\epsilon }^{2}\to S_{\epsilon }^{3}$
is a map germ of fold type, then its associated link $f|_{\widetilde {S}_{\epsilon }^{2}}\colon \widetilde {S}_{\epsilon }^{2}\to S_{\epsilon }^{3}$![]() is folded.
is folded.
We can assume that $f(x,y,z)=(x,y,z^{2},zp(x,y,z^{2}))$![]() , so it satisfies conditions (1), (2), (3) and (4) of remark 3.4. Moreover, we have a commutative diagram where $\psi (P)=P/\sqrt \epsilon$
, so it satisfies conditions (1), (2), (3) and (4) of remark 3.4. Moreover, we have a commutative diagram where $\psi (P)=P/\sqrt \epsilon$![]() and $\phi$
and $\phi$![]() is some diffeomorphism. Since
is some diffeomorphism. Since
we can choose $\phi$![]() in such a way that it preserves the symmetry with respect to the plane $z=0$
in such a way that it preserves the symmetry with respect to the plane $z=0$![]() . This implies that $\gamma$
. This implies that $\gamma$![]() is folded.
is folded.
Example 5.4 Let us examine some examples of links of map germs $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() of fold type.
of fold type.
(1) Let $\gamma \colon S^{2}\to S^{3}$
 be the link of the immersion $f(x,y,z)=(x,y,z,0)$
be the link of the immersion $f(x,y,z)=(x,y,z,0)$ . Then $D(\gamma )=\emptyset$
. Then $D(\gamma )=\emptyset$ , so the dual tree has just one vertex (figure 6).
, so the dual tree has just one vertex (figure 6).(2) Let $\gamma \colon S^{2}\to S^{3}$
 be the link of the cross cap $f(x,y,z)=(x,y,z^{2},xz)$
be the link of the cross cap $f(x,y,z)=(x,y,z^{2},xz)$ . Then $\gamma (D(\gamma ))$
. Then $\gamma (D(\gamma ))$ has one connected component (a segment) and as consequence $S^{2}_+{\setminus} \gamma (D(\gamma ))$
has one connected component (a segment) and as consequence $S^{2}_+{\setminus} \gamma (D(\gamma ))$ has two connected components in the border. Therefore the dual tree of $\gamma$
has two connected components in the border. Therefore the dual tree of $\gamma$ has two vertices, both of type $\ast$
has two vertices, both of type $\ast$ (figure 7).
(figure 7).(3) Let $\gamma \colon S^{2}\to S^{3}$
 be the link of the map germ $f(x,y,z)=(x,y,z^{2},z(x^{2}+ y^{2}-z^{2}))$
be the link of the map germ $f(x,y,z)=(x,y,z^{2},z(x^{2}+ y^{2}-z^{2}))$ . Then $\gamma (D(\gamma ))$
. Then $\gamma (D(\gamma ))$ has one connected component (a closed curve) and as consequence $S^{2}_+{\setminus} \gamma (D(\gamma ))$
has one connected component (a closed curve) and as consequence $S^{2}_+{\setminus} \gamma (D(\gamma ))$ has two connected components, one in the border. Therefore the dual tree of $\gamma$
has two connected components, one in the border. Therefore the dual tree of $\gamma$ has two vertices, one of type $\ast$
has two vertices, one of type $\ast$ and one of type $\bullet$
and one of type $\bullet$ (figure 8).
(figure 8).(4) Let $\gamma \colon S^{2}\to S^{3}$
 be the link of the map germ $f(x,y,z)=(x,y,z^{2},z(x^{2}- y^{2}+z^{2}))$
be the link of the map germ $f(x,y,z)=(x,y,z^{2},z(x^{2}- y^{2}+z^{2}))$ . Then $\gamma (D(\gamma ))$
. Then $\gamma (D(\gamma ))$ has two connected components (both a segment) and as consequence $S^{2}_+{\setminus} \gamma (D(\gamma ))$
has two connected components (both a segment) and as consequence $S^{2}_+{\setminus} \gamma (D(\gamma ))$ has three connected components, all in the border. Therefore the dual tree of $\gamma$
has three connected components, all in the border. Therefore the dual tree of $\gamma$ has three vertices, all of them of type $\ast$
has three vertices, all of them of type $\ast$ (figure 9).
(figure 9).
In order to simplify the notation, given a folded stable map $\gamma \colon S^{2}\to S^{3}$![]() , we denote by $t(\gamma )$
, we denote by $t(\gamma )$![]() the associated dual tree and by $\simeq$
the associated dual tree and by $\simeq$![]() the equivalence relation between dual trees.
the equivalence relation between dual trees.

Figure 6. Dual tree of the link of the regular map.

Figure 7. Dual tree of the link of the cross cap.

Figure 8. Dual tree of the link of the map germ $(x,y,z^2,z(x^2+y^2-z^2))$![]() .
.

Figure 9. Dual tree of the link of the map germ $(x,y,z^2,z(x^2-y^2+z^2))$![]() .
.
Before proving the main result of this section, we need to verify that for any mosaic $(D^{2},K)$![]() we can find a folded stable map $\gamma$
we can find a folded stable map $\gamma$![]() such that $(S^{2}_+, \gamma (D(\gamma )))$
such that $(S^{2}_+, \gamma (D(\gamma )))$![]() is equivalent to $(D^{2},K)$
is equivalent to $(D^{2},K)$![]() . To do this, we define two operations in $\gamma$
. To do this, we define two operations in $\gamma$![]() , associated to the elimination or addition of a final vertex in its dual tree.
, associated to the elimination or addition of a final vertex in its dual tree.
Let $\gamma \colon S^{2}\to S^{3}$![]() be a folded stable map. Let $v_i$
be a folded stable map. Let $v_i$![]() be a final vertex in its dual tree $t(\gamma )$
be a final vertex in its dual tree $t(\gamma )$![]() . We construct a new folded stable map $\gamma '$
. We construct a new folded stable map $\gamma '$![]() such that $t(\gamma ')$
such that $t(\gamma ')$![]() is obtained from $t(\gamma )$
is obtained from $t(\gamma )$![]() after eliminating the vertex $v_i$
after eliminating the vertex $v_i$![]() . We have two cases:
. We have two cases:
$v_i$ is of type $\bullet$
is of type $\bullet$
We construct $\gamma '$![]() with the aid of the symmetric version of the miniversal unfolding of the bigerm of $\mathcal {A}_e$
with the aid of the symmetric version of the miniversal unfolding of the bigerm of $\mathcal {A}_e$![]() -codimension 1 given by two regular branches having a contact of type $x^{2}+y^{2}$
-codimension 1 given by two regular branches having a contact of type $x^{2}+y^{2}$![]() . More explicitly, we consider the family $f_t\colon \mathbb {R}^{2}\amalg \mathbb {R}^{2}\to \mathbb {R}^{3}$
. More explicitly, we consider the family $f_t\colon \mathbb {R}^{2}\amalg \mathbb {R}^{2}\to \mathbb {R}^{3}$![]() , with $t\in \mathbb {R}$
, with $t\in \mathbb {R}$![]() , given by
, given by

We now consider the restriction $f_t\colon f_t^{-1}(D^{3})\to D^{3}$![]() , where $D^{3}$
, where $D^{3}$![]() is the unit closed disc centred at the origin in $\mathbb {R}^{3}$
is the unit closed disc centred at the origin in $\mathbb {R}^{3}$![]() . The image of this map can be seen in figure 10 for $t>0$
. The image of this map can be seen in figure 10 for $t>0$![]() (left), $t=0$
(left), $t=0$![]() (centre) and $t<0$
(centre) and $t<0$![]() (right).
(right).

Figure 10. Image of $f_t$![]() .
.
The final vertex $v_i$![]() corresponds to a connected component of $S^{2}_+{\setminus} \gamma (D(\gamma ))$
corresponds to a connected component of $S^{2}_+{\setminus} \gamma (D(\gamma ))$![]() whose boundary is a simple closed curve $D$
whose boundary is a simple closed curve $D$![]() in the interior of $S^{2}_+$
in the interior of $S^{2}_+$![]() . We can choose a closed 3-ball $B$
. We can choose a closed 3-ball $B$![]() in $S^{3}$
in $S^{3}$![]() which contains $D$
which contains $D$![]() in its interior, is symmetric with respect to $T=0$
in its interior, is symmetric with respect to $T=0$![]() and such that the restriction $\gamma \colon \gamma ^{-1}(B)\to B$
and such that the restriction $\gamma \colon \gamma ^{-1}(B)\to B$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to the mapping $f_t:f_t^{-1}(D^{3})\to D^{3}$
-equivalent to the mapping $f_t:f_t^{-1}(D^{3})\to D^{3}$![]() , with $t>0$
, with $t>0$![]() . We define $\gamma '\colon S^{2}\to S^{3}$
. We define $\gamma '\colon S^{2}\to S^{3}$![]() as the folded stable map that coincides with $\gamma$
as the folded stable map that coincides with $\gamma$![]() in an open neighbourhood of $B$
in an open neighbourhood of $B$![]() and $\gamma '\colon \gamma '^{-1}(B)\to B$
and $\gamma '\colon \gamma '^{-1}(B)\to B$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$
-equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$![]() , with $t<0$
, with $t<0$![]() . Certainly we can do this in a smooth way.
. Certainly we can do this in a smooth way.
We can also perform the inverse operation. Given any folded stable map $\gamma '\colon S^{2}\to S^{3}$![]() and given any vertex $v_j$
and given any vertex $v_j$![]() in $t(\gamma ')$
in $t(\gamma ')$![]() , we can construct a new folded stable map $\gamma \colon S^{2}\to S^{3}$
, we can construct a new folded stable map $\gamma \colon S^{2}\to S^{3}$![]() such that $t(\gamma )$
such that $t(\gamma )$![]() is obtained after connecting a new final vertex of type $\bullet$
is obtained after connecting a new final vertex of type $\bullet$![]() to the vertex $v_j$
to the vertex $v_j$![]() . In this case, we take a closed 3-ball $B$
. In this case, we take a closed 3-ball $B$![]() in $S^{3}$
in $S^{3}$![]() symmetric with respect to $T=0$
symmetric with respect to $T=0$![]() and such that the restriction $\gamma '\colon \gamma '^{-1}(B)\to B$
and such that the restriction $\gamma '\colon \gamma '^{-1}(B)\to B$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$
-equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$![]() , with $t<0$
, with $t<0$![]() . As before, we define $\gamma \colon S^{2}\to S^{3}$
. As before, we define $\gamma \colon S^{2}\to S^{3}$![]() as the folded stable map that coincides with $\gamma '$
as the folded stable map that coincides with $\gamma '$![]() in an open neighbourhood of $B$
in an open neighbourhood of $B$![]() and $\gamma \colon \gamma ^{-1}(B)\to B$
and $\gamma \colon \gamma ^{-1}(B)\to B$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$
-equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$![]() , with $t>0$
, with $t>0$![]() .
.
We observe that the two operations are uniquely defined and are inverse up to $\mathcal {A}$![]() -equivalence. That is, if we eliminate in $\gamma$
-equivalence. That is, if we eliminate in $\gamma$![]() a final vertex of type $\bullet$
a final vertex of type $\bullet$![]() connected to some other vertex $v_j$
connected to some other vertex $v_j$![]() and we add a new final vertex of type $\bullet$
and we add a new final vertex of type $\bullet$![]() connected to $v_j$
connected to $v_j$![]() , then the resulting map is $\mathcal {A}$
, then the resulting map is $\mathcal {A}$![]() -equivalent to $\gamma$
-equivalent to $\gamma$![]() . Analogously, the same happens if we first add a new final vertex of type $\bullet$
. Analogously, the same happens if we first add a new final vertex of type $\bullet$![]() and then we eliminate that vertex.
and then we eliminate that vertex.
$v_i$ is of type $\ast$
is of type $\ast$
In this case we use the miniversal unfolding of the monogerm of $\mathcal {A}_e$![]() -codimension 1 of type $S^{+}_1$
-codimension 1 of type $S^{+}_1$![]() in Mond's classification [Reference Mond13]. The usual normal form of this class is already symmetric and is the family $f_t\colon \mathbb {R}^{2}\to \mathbb {R}^{3}$
in Mond's classification [Reference Mond13]. The usual normal form of this class is already symmetric and is the family $f_t\colon \mathbb {R}^{2}\to \mathbb {R}^{3}$![]() , with $t\in \mathbb {R}$
, with $t\in \mathbb {R}$![]() , given by
, given by
As before, we take the restriction $f_t\colon f_t^{-1}(D^{3})\to D^{3}$![]() . We see the image of $f_t$
. We see the image of $f_t$![]() in figure 11 for $t>0$
in figure 11 for $t>0$![]() (left), $t=0$
(left), $t=0$![]() (centre) and $t<0$
(centre) and $t<0$![]() (right).
(right).

Figure 11. Image of $f_t$![]() .
.
The final vertex $v_i$![]() corresponds now to a connected component of $S^{2}_+{\setminus} \gamma (D(\gamma ))$
corresponds now to a connected component of $S^{2}_+{\setminus} \gamma (D(\gamma ))$![]() bounded by a simple arc $C$
bounded by a simple arc $C$![]() with ends in the boundary of $S^{2}_+$
with ends in the boundary of $S^{2}_+$![]() . We proceed as in the previous case. We take a closed 3-ball $B$
. We proceed as in the previous case. We take a closed 3-ball $B$![]() in $S^{3}$
in $S^{3}$![]() which contains $C$
which contains $C$![]() in its interior, is symmetric with respect to $T=0$
in its interior, is symmetric with respect to $T=0$![]() and such that the restriction $\gamma \colon \gamma ^{-1}(B)\to B$
and such that the restriction $\gamma \colon \gamma ^{-1}(B)\to B$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$
-equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$![]() , with $t>0$
, with $t>0$![]() . We define $\gamma '\colon S^{2}\to S^{3}$
. We define $\gamma '\colon S^{2}\to S^{3}$![]() as the folded stable map that coincides with $\gamma$
as the folded stable map that coincides with $\gamma$![]() in an open neighbourhood of $B$
in an open neighbourhood of $B$![]() and $\gamma '\colon \gamma '^{-1}(B)\to B$
and $\gamma '\colon \gamma '^{-1}(B)\to B$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$
-equivalent to the mapping $f_t\colon f_t^{-1}(D^{3})\to D^{3}$![]() , with $t<0$
, with $t<0$![]() .
.
The inverse operation is defined in an analogous way. Given $\gamma '$![]() and a vertex $v_j\in t(\gamma ')$
and a vertex $v_j\in t(\gamma ')$![]() of type $\ast$
of type $\ast$![]() , we construct $\gamma$
, we construct $\gamma$![]() such that $t(\gamma )$
such that $t(\gamma )$![]() is obtained after adding a new vertex of type $\ast$
is obtained after adding a new vertex of type $\ast$![]() connected to $v_j$
connected to $v_j$![]() . As before, the two operations are uniquely defined and are inverse up to $\mathcal {A}$
. As before, the two operations are uniquely defined and are inverse up to $\mathcal {A}$![]() -equivalence.
-equivalence.
Lemma 5.5 Let $(D^{2},K)$![]() be a mosaic of a 2-disc $D^{2}$
be a mosaic of a 2-disc $D^{2}$![]() . Then, there exists a folded stable map $\gamma \colon S^{2}\to S^{3}$
. Then, there exists a folded stable map $\gamma \colon S^{2}\to S^{3}$![]() such that $(S^{2}_+, \gamma (D(\gamma ))$
such that $(S^{2}_+, \gamma (D(\gamma ))$![]() is equivalent to $(D^{2},K)$
is equivalent to $(D^{2},K)$![]() .
.
Proof. We prove it by induction on the number of vertices of the associated dual tree of $(D^{2},K)$![]() . For mosaics with dual trees of 1 and 2 vertices this is proved by example 5.4. Let us suppose the result is true for mosaics with dual trees of $v$
. For mosaics with dual trees of 1 and 2 vertices this is proved by example 5.4. Let us suppose the result is true for mosaics with dual trees of $v$![]() vertices. If the dual tree $\Gamma$
vertices. If the dual tree $\Gamma$![]() of $(D^{2},K)$
of $(D^{2},K)$![]() has $v+1$
has $v+1$![]() vertices we can eliminate a final vertex of $\Gamma$
vertices we can eliminate a final vertex of $\Gamma$![]() , obtaining the dual tree $\Gamma '$
, obtaining the dual tree $\Gamma '$![]() of a mosaic $(D^{2},K')$
of a mosaic $(D^{2},K')$![]() , where $\Gamma '$
, where $\Gamma '$![]() has $v$
has $v$![]() vertices. By induction hypothesis there exists a stable map $\gamma '\colon S^{2}\to S^{3}$
vertices. By induction hypothesis there exists a stable map $\gamma '\colon S^{2}\to S^{3}$![]() that is folded, such that $(S^{2}_+, \gamma '(D(\gamma '))$
that is folded, such that $(S^{2}_+, \gamma '(D(\gamma '))$![]() is equivalent to $(D^{2}, K')$
is equivalent to $(D^{2}, K')$![]() . Applying to $\gamma '$
. Applying to $\gamma '$![]() an operation of type 1 or 2, depending if the eliminated final vertex was of type $\bullet$
an operation of type 1 or 2, depending if the eliminated final vertex was of type $\bullet$![]() or $\ast$
or $\ast$![]() respectively, we get a folded stable map $\gamma$
respectively, we get a folded stable map $\gamma$![]() and $(S^{2}_+, \gamma (D(\gamma ))$
and $(S^{2}_+, \gamma (D(\gamma ))$![]() is equivalent to $(D^{2}, K).$
is equivalent to $(D^{2}, K).$![]()
Now, we are in conditions of stating and proving the main result of this section
Theorem 5.6 Let $\gamma,\delta \colon S^{2}\to S^{3}$![]() be two folded stable maps. Then $\gamma$
be two folded stable maps. Then $\gamma$![]() and $\delta$
and $\delta$![]() are topologically equivalent if and only if their respective dual trees are equivalent.
are topologically equivalent if and only if their respective dual trees are equivalent.
Proof. Let $\gamma,\delta \colon S^{2}\to S^{3}$![]() be two folded stable maps that are $\mathcal {C}^{0}$
be two folded stable maps that are $\mathcal {C}^{0}$![]() -$\mathcal {A}$
-$\mathcal {A}$![]() -equivalent. There exist homeomorphisms $\alpha \colon S^{2}\to S^{2}$
-equivalent. There exist homeomorphisms $\alpha \colon S^{2}\to S^{2}$![]() and $\beta \colon S^{3}\to S^{3}$
and $\beta \colon S^{3}\to S^{3}$![]() such that $\delta =\beta \circ \gamma \circ \alpha ^{-1}$
such that $\delta =\beta \circ \gamma \circ \alpha ^{-1}$![]() . We start with $\gamma$
. We start with $\gamma$![]() and we assign a vertex $v_i$
and we assign a vertex $v_i$![]() to each connected component of $S_+^{2}{\setminus} \gamma (D(\gamma ))$
to each connected component of $S_+^{2}{\setminus} \gamma (D(\gamma ))$![]() . Since $\beta$
. Since $\beta$![]() sends connected components of $S_+^{2}{\setminus} \gamma (D(\gamma ))$
sends connected components of $S_+^{2}{\setminus} \gamma (D(\gamma ))$![]() to connected components of $S_+^{2}{\setminus} \delta (D(\delta ))$
to connected components of $S_+^{2}{\setminus} \delta (D(\delta ))$![]() , we can choose for each connected component of $S_+^{2}{\setminus} \delta (D(\delta ))$
, we can choose for each connected component of $S_+^{2}{\setminus} \delta (D(\delta ))$![]() the same vertex. With these choices we have that $v_iv_j$
the same vertex. With these choices we have that $v_iv_j$![]() is an edge of $t(\gamma )$
is an edge of $t(\gamma )$![]() if and only if it is an edge of $t(\delta )$
if and only if it is an edge of $t(\delta )$![]() and, as a consequence, both dual trees are equal.
and, as a consequence, both dual trees are equal.
We prove the converse by induction on the number of vertices of $t(\gamma )$![]() . If $t(\gamma )$
. If $t(\gamma )$![]() has only one vertex, it must be of type $\ast$
has only one vertex, it must be of type $\ast$![]() . This implies, by hypothesis, that $\gamma (D(\gamma ))=\delta (D(\delta ))=\emptyset$
. This implies, by hypothesis, that $\gamma (D(\gamma ))=\delta (D(\delta ))=\emptyset$![]() . Therefore, $\gamma$
. Therefore, $\gamma$![]() and $\delta$
and $\delta$![]() are embeddings. Then, by the generalized Schönflies theorem [Reference Brown3], $\gamma (S^{2})$
are embeddings. Then, by the generalized Schönflies theorem [Reference Brown3], $\gamma (S^{2})$![]() and $\delta (S^{2})$
and $\delta (S^{2})$![]() are unknotted in $S^{3}$
are unknotted in $S^{3}$![]() , and, as a consequence, $\gamma$
, and, as a consequence, $\gamma$![]() and $\delta$
and $\delta$![]() are topologically equivalent.
are topologically equivalent.
Let us suppose the result is true for $v$![]() vertices. If $t(\gamma )$
vertices. If $t(\gamma )$![]() has $v+1$
has $v+1$![]() vertices, we eliminate a final vertex. The new graph has $v$
vertices, we eliminate a final vertex. The new graph has $v$![]() vertices and is the dual tree of a stable map $\gamma '\colon S^{2}\to S^{3}$
vertices and is the dual tree of a stable map $\gamma '\colon S^{2}\to S^{3}$![]() obtained from $\gamma$
obtained from $\gamma$![]() by applying an operation of type 1 or 2, depending if the eliminated final vertex was of type $\bullet$
by applying an operation of type 1 or 2, depending if the eliminated final vertex was of type $\bullet$![]() or $\ast$
or $\ast$![]() respectively. If we eliminate the corresponding final vertex in $t(\delta )$
respectively. If we eliminate the corresponding final vertex in $t(\delta )$![]() we obtain a new graph with $v$
we obtain a new graph with $v$![]() vertices, that is the dual tree of a stable map $\delta '$
vertices, that is the dual tree of a stable map $\delta '$![]() obtained by applying the correspondent operation to $\delta$
obtained by applying the correspondent operation to $\delta$![]() . By induction hypothesis, $\gamma '$
. By induction hypothesis, $\gamma '$![]() and $\delta '$
and $\delta '$![]() are topologically equivalent. We apply the same movement to both stable maps to undo the last operation, obtaining that $\gamma$
are topologically equivalent. We apply the same movement to both stable maps to undo the last operation, obtaining that $\gamma$![]() and $\delta$
and $\delta$![]() are topologically equivalent.
are topologically equivalent.
Remark 5.7 Let $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() be an analytic map germ with isolated instability of fold type, that is, $f$
be an analytic map germ with isolated instability of fold type, that is, $f$![]() can be written in the form $(x,y,z^{2},zp(x,y,z^{2}))$
can be written in the form $(x,y,z^{2},zp(x,y,z^{2}))$![]() . We can choose a good representative $f:U\to V$
. We can choose a good representative $f:U\to V$![]() such that $U$
such that $U$![]() and $V$
and $V$![]() are homeomorphic to the closed 3-ball and 4-ball, respectively, $D(f)\subset U$
are homeomorphic to the closed 3-ball and 4-ball, respectively, $D(f)\subset U$![]() , $f(D(f))\subset V\cap \{T=0\}\subset \mathbb {R}^{3}$
, $f(D(f))\subset V\cap \{T=0\}\subset \mathbb {R}^{3}$![]() are simply connected and $f(D(f))=CC_1\sqcup \cdots \sqcup CC_k\sqcup CD_1\sqcup \cdots \sqcup CD_j$
are simply connected and $f(D(f))=CC_1\sqcup \cdots \sqcup CC_k\sqcup CD_1\sqcup \cdots \sqcup CD_j$![]() , where $CC_i$
, where $CC_i$![]() is the cone of a segment that starts and ends at $Z=0$
is the cone of a segment that starts and ends at $Z=0$![]() and $CD_i$
and $CD_i$![]() is the cone of a simple closed curve $D_i$
is the cone of a simple closed curve $D_i$![]() . We define a graph $\Gamma = (V,E)$
. We define a graph $\Gamma = (V,E)$![]() where $v_i\in V$
where $v_i\in V$![]() is associated to each one of the connected components of $V\cap \{T=0\}{\setminus} f(D(f))$
is associated to each one of the connected components of $V\cap \{T=0\}{\setminus} f(D(f))$![]() and $v_iv_j$
and $v_iv_j$![]() is an edge of $\Gamma$
is an edge of $\Gamma$![]() if and only if the respective connected components are separated from each other by a connected component of $f(D(f))$
if and only if the respective connected components are separated from each other by a connected component of $f(D(f))$![]() . We have that $\Gamma$
. We have that $\Gamma$![]() is a tree that coincides with the tree of the associated link of $f$
is a tree that coincides with the tree of the associated link of $f$![]() , $t(f|_{S_{\epsilon }^{2}}).$
, $t(f|_{S_{\epsilon }^{2}}).$![]()
Applying last results we have the converse of corollary 2.5 for map germs of fold type.
Theorem 5.8 Let $f,g\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() be analytic map germs with isolated instability of fold type. Then, if $f$
be analytic map germs with isolated instability of fold type. Then, if $f$![]() and $g$
and $g$![]() are topologically equivalent, their associated links are topologically equivalent.
are topologically equivalent, their associated links are topologically equivalent.
Proof. We choose a good representative of $f$![]() in the sense of remark 5.7. Since $f$
in the sense of remark 5.7. Since $f$![]() and $g$
and $g$![]() are topologically equivalent, we get a representative of $g$
are topologically equivalent, we get a representative of $g$![]() , $g\colon U'\to V'$
, $g\colon U'\to V'$![]() such that $U'$
such that $U'$![]() and $V'$
and $V'$![]() are homeomorphic to the closed 3-ball and 4-ball, respectively and $D(g)\subset U'$
are homeomorphic to the closed 3-ball and 4-ball, respectively and $D(g)\subset U'$![]() , $g(D(g))\subset V'\cap \{T=0\}\subset \mathbb {R}^{3}$
, $g(D(g))\subset V'\cap \{T=0\}\subset \mathbb {R}^{3}$![]() are simply connected. We define its corresponding associated graph $\Gamma '$
are simply connected. We define its corresponding associated graph $\Gamma '$![]() , a tree that coincides with the tree of the associated link of $g$
, a tree that coincides with the tree of the associated link of $g$![]() . Using again the topological equivalence of $f$
. Using again the topological equivalence of $f$![]() and $g$
and $g$![]() we get that the dual trees of their associated links, $t(f|_{\widetilde {S}_{\epsilon }^{2}})$
we get that the dual trees of their associated links, $t(f|_{\widetilde {S}_{\epsilon }^{2}})$![]() and $t(g|_{\widetilde {S}_{\epsilon }^{2}})$
and $t(g|_{\widetilde {S}_{\epsilon }^{2}})$![]() are equal. Applying theorem 5.6, this directly implies that both links are topologically equivalent.
are equal. Applying theorem 5.6, this directly implies that both links are topologically equivalent.
Putting together theorems 5.6 and 5.8, and corollary 2.5, we have the following result.
Corollary 5.9 Let $f,g\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() be analytic map germs with isolated instability of fold type. Then, $f$
be analytic map germs with isolated instability of fold type. Then, $f$![]() and $g$
and $g$![]() are topologically equivalent if and only if the dual trees of their associated links are equivalent.
are topologically equivalent if and only if the dual trees of their associated links are equivalent.
6. Topological classification of map germs of fold type
Given an analytic map germ with isolated instability $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() of fold type, we want to study its topological type by means of the dual tree of its link. We are going to give a complete list of topological classes for fold maps with associated dual trees up to 4 vertices and to indicate how to obtain the normal form associated to any dual tree of a folded stable map $\gamma \colon S^{2}\to S^{3}$
of fold type, we want to study its topological type by means of the dual tree of its link. We are going to give a complete list of topological classes for fold maps with associated dual trees up to 4 vertices and to indicate how to obtain the normal form associated to any dual tree of a folded stable map $\gamma \colon S^{2}\to S^{3}$![]()
Remark 6.1 Let $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() be an analytic map germ with isolated instability of fold type $f(x,y,z) = (x,y,z^{2},zp(x,y,z^{2}))$
be an analytic map germ with isolated instability of fold type $f(x,y,z) = (x,y,z^{2},zp(x,y,z^{2}))$![]() such that the associated dual tree of its link has at most 4 vertices. Then, $f$
such that the associated dual tree of its link has at most 4 vertices. Then, $f$![]() is topologically equivalent to one of the germs of tables I and II. They are computed by software Mathematica.
is topologically equivalent to one of the germs of tables I and II. They are computed by software Mathematica.
TABLE I. Topological classes up to 4 vertices.

TABLE II. Topological classes up to 4 vertices.

Remark 6.2 Let $f\colon (\mathbb {R}^{3},0)\to (\mathbb {R}^{4},0)$![]() be an analytic map germ with isolated instability of fold type $f(x,y,z) = (x,y,z^{2},zp(x,y,z^{2}))$
be an analytic map germ with isolated instability of fold type $f(x,y,z) = (x,y,z^{2},zp(x,y,z^{2}))$![]() such that $f(D(f))$
such that $f(D(f))$![]() has $k+j$
has $k+j$![]() connected components, $k$
connected components, $k$![]() contained in $\{Z>0\}$
contained in $\{Z>0\}$![]() and $j$
and $j$![]() intersecting $\{Z=0\}$
intersecting $\{Z=0\}$![]() . Then, we can find suitable coefficients $A_i,B_i,C_i,D_i, E_i,$
. Then, we can find suitable coefficients $A_i,B_i,C_i,D_i, E_i,$![]() $1\leq i\leq k+j$
$1\leq i\leq k+j$![]() such that $f$
such that $f$![]() is topologically equivalent to a germ whose double point space $D(f)$
is topologically equivalent to a germ whose double point space $D(f)$![]() is given by an equation of the form $F_1\cdots F_{k+j}$
is given by an equation of the form $F_1\cdots F_{k+j}$![]() , where
, where

Proof. First of all, we see that we can find $\epsilon _0> 0$![]() small enough such that if $i\neq r$
small enough such that if $i\neq r$![]() , $F_i\cap F_r\cap S_{\epsilon }^{2} =\emptyset$
, $F_i\cap F_r\cap S_{\epsilon }^{2} =\emptyset$![]() , for any $0<\epsilon \leq \epsilon _0$
, for any $0<\epsilon \leq \epsilon _0$![]() . Otherwise, we would have closed curves contained in $F_i\cap F_r$
. Otherwise, we would have closed curves contained in $F_i\cap F_r$![]() as near as we want to the origin and as a consequence, applying the Curve Selection Lemma, we would have a surface contained in $F_i\cap F_r$
as near as we want to the origin and as a consequence, applying the Curve Selection Lemma, we would have a surface contained in $F_i\cap F_r$![]() , which is a contradiction with the fact that for any $\delta >0$
, which is a contradiction with the fact that for any $\delta >0$![]() we always can choose generic coefficients $A_i,B_i,C_i,D_i,E_i, A_r,B_r,C_r,D_r,E_r$
we always can choose generic coefficients $A_i,B_i,C_i,D_i,E_i, A_r,B_r,C_r,D_r,E_r$![]() such that $F_i\cap F_r\cap S_{\delta }^{2} =\emptyset$
such that $F_i\cap F_r\cap S_{\delta }^{2} =\emptyset$![]() .
.
Now, we proof the result by induction. Applying last remark we know that the result is true for $k+j\leq 3$![]() . If we suppose that the result is true for a map germ $f$
. If we suppose that the result is true for a map germ $f$![]() such that $f(D(f))$
such that $f(D(f))$![]() has $k+j$
has $k+j$![]() connected components, we can get a normal form for a map germ $f'$
connected components, we can get a normal form for a map germ $f'$![]() such that $f'(D(f'))=f(D(f))\sqcup F$
such that $f'(D(f'))=f(D(f))\sqcup F$![]() where $F$
where $F$![]() is a connected component of $f'(D(f'))$
is a connected component of $f'(D(f'))$![]() just by adding to the equation of $D(f)$
just by adding to the equation of $D(f)$![]() a factor of the form $(Ax^{2}+By^{2}+Cz^{4}+Dxz^{2}+Eyz^{2})$
a factor of the form $(Ax^{2}+By^{2}+Cz^{4}+Dxz^{2}+Eyz^{2})$![]() if $F$
if $F$![]() is contained in $\{Z>0\}$
is contained in $\{Z>0\}$![]() or of the form $(A_x^{2}+By^{2}+Cz^{2}+Dx+Ey)$
or of the form $(A_x^{2}+By^{2}+Cz^{2}+Dx+Ey)$![]() if $F$
if $F$![]() intersects $\{Z=0\}$
intersects $\{Z=0\}$![]() , with $A,B,C,D, E$
, with $A,B,C,D, E$![]() chosen in a convenient way.
chosen in a convenient way.
Acknowledgments
Grant PGC2018-094889-B-100 funded by MCIN/AEI/10.13039/501100011033 and by ‘ERDF A way of making Europe.’