Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T06:08:02.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Dual exponential polynomials and a problem of Ozawa

Part of: Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  16 June 2021

Janne Heittokangas ,
Katsuya Ishizaki ,
Kazuya Tohge  and
Zhi-Tao Wen
Janne Heittokangas
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, P.O. Box 111, 80101 Joensuu, Finland ([email protected])
Katsuya Ishizaki
Affiliation:
Faculty of Liberal Arts, The Open University of Japan, Mihama-ku, Chiba, Japan ([email protected])
Kazuya Tohge
Affiliation:
College of Science and Engineering, Kanazawa University, Kakuma-machi, Kanazawa 920-1192, Japan ([email protected])
Zhi-Tao Wen*
Affiliation:
Department of Mathematics, Shantou University, Daxue Road No. 243, Shantou 515063, China ([email protected])
*
*Corresponding author
Get access Rights & Permissions [Opens in a new window]

Abstract

Complex linear differential equations with entire coefficients are studied in the situation where one of the coefficients is an exponential polynomial and dominates the growth of all the other coefficients. If such an equation has an exponential polynomial solution 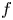$f$, then the order of 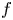$f$ and of the dominant coefficient are equal, and the two functions possess a certain duality property. The results presented in this paper improve earlier results by some of the present authors, and the paper adjoins with two open problems.

Keywords

Dual exponential polynomialsexponential sumfinite orderlinear differential equationOzawa's problemvalue distribution

MSC classification

Primary: 30D15: Special classes of entire functions and growth estimates
Secondary: 30D35: Distribution of values, Nevanlinna theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 701 - 719
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amemiya, I. and Ozawa, M.. Non-existence of finite order solutions of $w''+\textrm {e}^{-}zw'+Q(z)w=0$. Hokkaido Math. J. 10 (1981), Special Issue, 1–17.Google Scholar
Frei, M.. Über die subnormalen Lösungen der Differentialgleichung $w''+\textrm {e}^{-}zw'+konst\cdot w=0$. Comment. Math. Helv. 36 (1961), 1–8.CrossRefGoogle Scholar
Gross, F.. Factorization of meromorphic functions (Washington, DC: Mathematics Research Center, Naval Research Laboratory, 1972).Google Scholar
Gundersen, G. G.. On the question of whether $f''+\textrm {e}^{-}zf'+B(z)f=0$ can admit a solution $f\not \equiv 0$ of finite order. Proc. Roy. Soc. Edinburgh Sect. A 102 (1986), 9–17.CrossRefGoogle Scholar
Gundersen, G. G.. Finite order solutions of second order linear differential equations. Trans. Am. Math. Soc. 305 (1988), 415–429.CrossRefGoogle Scholar
Gundersen, G. G.. Estimates for the logarithmic derivative of a meromorphic function plus similar estimates. J. London Math. Soc. (2) 37 (1988), 88–104.CrossRefGoogle Scholar
Gundersen, G. G., Steinbart, E. and Wang, S.. The possible orders of solutions of linear differential equations with polynomial coefficients. Trans. Am. Math. Soc. 350 (1998), 1225–1247.CrossRefGoogle Scholar
Heittokangas, J., Ishizaki, K., Tohge, K. and Wen, Z.-T.. Zero distribution and division results for exponential polynomials. Israel J. Math. 227 (2018), 397–421.CrossRefGoogle Scholar
Heittokangas, J., Laine, I., Tohge, K. and Wen, Z.-T.. Completely regular growth solutions of second order complex linear differential equations. Ann. Acad. Sci. Fenn. Math. 40 (2015), 985–1003.CrossRefGoogle Scholar
Heittokangas, J. and Wen, Z.-T.. Generalization of Pólya's zero distribution theory for exponential polynomials, and sharp results for asymptotic growth. Comput. Methods Funct. Theory. 21 (2021), 245–270.CrossRefGoogle Scholar
Langer, R. E.. On the zeros of exponential sums and integrals. Bull. Am. Math. Soc. 37 (1931), 213–239.CrossRefGoogle Scholar
Langley, J. K.. On complex oscillation and a problem of Ozawa. Kodai Math. J. 9 (1986), 430–439.CrossRefGoogle Scholar
Moreno, C. J.. The zeros of exponential polynomials. I. Compositio Math. 26 (1973), 69–78.Google Scholar
Nevanlinna, R.. Analytic Functions. Translated from the second German edition by Phillip Emig. Die Grundlehren der mathematischen Wissenschaften, Band 162 (New York-Berlin: Springer-Verlag, 1970).Google Scholar
Ozawa, M.. On a solution of $w''+\textrm {e}^{-}zw'+(az+b)w=0$. Kodai Math. J. 3 (1980), 295–309.Google Scholar
Steinmetz, N.. Zur wertverteilung von exponentialpolynomen. Manuscripta Math. 26 (1978/79), 155–167.CrossRefGoogle Scholar
Steinmetz, N.. Zur Wertverteilung der quotienten von exponentialpolynomen. Arch. Math. 35( 1980), 461–470.CrossRefGoogle Scholar
Wen, Z.-T., Gundersen, G. G. and Heittokangas, J.. Dual exponential polynomials and linear differential equations. J. Differ. Equ. 264 (2018), 98–114.CrossRefGoogle Scholar