Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T04:21:19.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclic parallel structure Jacobi operator for real hypersurfaces in complex two-plane Grassmannians

Part of: Global differential geometry

Published online by Cambridge University Press:  12 August 2021

Hyunjin Lee ,
Young Jin Suh  and
Changhwa Woo
Hyunjin Lee
Affiliation:
The Research Institute of Real and Complex Manifolds (RIRCM), Kyungpook National University, Daegu 41566, Repulic of Korea ([email protected])
Young Jin Suh
Affiliation:
Department of Mathematics & RIRCM, Kyungpook National University, Daegu 41566, Repulic of Korea ([email protected])
Changhwa Woo
Affiliation:
Department of Applied Mathematics, Pukyong National University, Busan 48513, Republic of Korea ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, from the property of Killing for structure Jacobi tensor 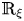$\mathbb {R}_{\xi }$, we introduce a new notion of cyclic parallelism of structure Jacobi operator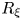$R_{\xi }$ on real hypersurfaces in the complex two-plane Grassmannians. By virtue of geodesic curves, we can give the equivalent relation between cyclic parallelism of 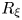$R_{\xi }$ and Killing property of 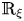$\mathbb {R}_{\xi }$. Then, we classify all Hopf real hypersurfaces with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians.

Keywords

Hopf real hypersurfacecomplex two-plane Grassmannians(quadratic) Killing tensorcyclic parallelismstructure Jacobi operator

MSC classification

Primary: 53C40: Global submanifolds
Secondary: 53C15: General geometric structures on manifolds (almost complex, almost product structures, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 4 , August 2022 , pp. 939 - 964
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, J. F.. Lectures on Exceptional Lie Groups. Chicago Lectures in Mathematics (Chicago, IL: University of Chicago Press, 1996).Google Scholar
Ballmann, W.. Lectures on Kähler Manifolds. ESI Lectures in Mathematics and Physics (Zürich: European Mathematical Society (EMS), 2006).CrossRefGoogle Scholar
Berndt, J.. Riemannian geometry of complex two-plane Grassmannians. Rend. Sem. Mat. Univ. Politec. Torino 55 (1997), 19–83.Google Scholar
Berndt, J. and Suh, Y. J.. Real hypersurfaces in complex two-plane Grassmannians. Monatsh. Math. 127 (1999), 1–14.CrossRefGoogle Scholar
Berndt, J. and Suh, Y. J.. Isometric flows on real hypersurfaces in complex two-plane Grassmannians. Monatsh. Math. 137 (2002), 87–98.CrossRefGoogle Scholar
Berndt, J. and Suh, Y. J.. Hypersurfaces in noncompact complex Grassmannians of rank two. Internat. J. Math. 23 (2012), 1250103 (35 pages).CrossRefGoogle Scholar
Berndt, J. and Suh, Y. J.. Real hypersurfaces with isometric Reeb flow in complex quadrics. Internat. J. Math. 24 (2013), 1350050, 18 pp.CrossRefGoogle Scholar
Berndt, J. and Suh, Y. J.. Real hypersurfaces with isometric Reeb flow in Kähler manifolds. Commun. Contemp. Math. 23 (2021) 1950039, 33 pp.CrossRefGoogle Scholar
Berndt, J. and Suh, Y. J.. Real hypersurfaces in Hermitian Symmetric Spaces, Advances in Analysis and Geometry, Editor in Chief, Jie Xiao, ©2021 Copyright-Text, Walter de Gruyter GmbH, Berlin/Boston (in Press).CrossRefGoogle Scholar
Borel, A. and De Siebenthal, J.. Les sous-groupes fermés de rang maximum des groupes de Lie clos. Comment. Math. Helv. 23 (1949), 200–221.CrossRefGoogle Scholar
Eberlein, P. B.. Geometry of Nonpositively Curved Manifolds. Chicago Lectures in Mathematics (Chicago, IL: University of Chicago Press, 1996).Google Scholar
Heil, K., Moroianu, A. and Semmelmann, U.. Killing and conformal Killing tensors. J. Geom. Phys. 106 (2016), 383–400.CrossRefGoogle Scholar
Jeong, I., Machado, C. J. G., Pérez, J. D. and Suh, Y. J.. Real hypersrufaces in complex two-plane Grassmannians with $\mathfrak D^{\bot }$-parallel structure Jacobi operator. Interant. J. Math. 22 (2011), 655–673.CrossRefGoogle Scholar
Jeong, I., Pérez, J. D., Suh, Y. J. and Woo, C.. Lie derivatives and Ricci tensor on real hypersurfaces in complex two-plane Grassmannians. Canad. Math. Bull. 61 (2018), 543–552.CrossRefGoogle Scholar
Kobayashi, S. and Nomizu, K.. Foundations of Differential Geometry, Vol. I. Reprint of the 1963 original, Wiley Classics Library, A Wiley-Interscience Publication (New York: John Wiley & Sons, Inc., 1996).Google Scholar
Lee, R.-H. and Loo, T.-H.. Hopf hypersurfaces in complex Grassmannians of rank two. Results Math. 71 (2017), 1083–1107.CrossRefGoogle Scholar
Lee, H. and Suh, Y. J.. Real hypersurfaces of type $(B)$in complex two-plane Grassmannians related to the Reeb vector. Bull. Korean Math. Soc. 47 (2010), 551–561.CrossRefGoogle Scholar
Lee, H. and Suh, Y. J.. Remarks on the components of the Reeb vector field for real hypersurfaces in complex two-plane Grassmannians, Proceedings of the 17th International Workshop on Differential Geometry and the 7th KNUGRG-OCAMI Differential Geometry Workshop, Vol. 17, 153–169, Natl. Inst. Math. Sci.(NIMS), Taej$\breve{o}$n, 2013.Google Scholar
Lee, H. and Suh, Y. J.. Reeb recurrent structure Jacobi operator on real hypersurfaces in complex two-plane Grassmannians, Hermitian-Grassmannian submanifolds, 69–82, Springer Proc. Math. Stat., 203, Springer, Singapore, 2017.CrossRefGoogle Scholar
Lee, H. and Suh, Y. J.. Cyclic parallel hypersurfaces in complex Grassmannians of rank 2. Internat. J. Math. 31 (2020), 2050014, 14 pp.CrossRefGoogle Scholar
Lee, H., Woo, C. and Suh, Y. J.. Quadratic Killing normal Jacobi operator for real hypersurfaces in complex Grassmannians of rank 2. J. Geom. Phys. 160 (2021), 103975, 14 pp.CrossRefGoogle Scholar
Machado, C. J. G. and Pérez, J. D.. On the structure vector field of a real hypersurface in complex two-plane Grassmannians. Cent. Eur. J. Math. 10 (2012), 451–455.CrossRefGoogle Scholar
Machado, C. J. G. and Pérez, J. D.. Real hypersurfaces in complex two-plane Grassmannians some of whose Jacobi operators are $\xi$-invariant. Internat. J. Math. 23 (2012), 1250002, 12 pp.CrossRefGoogle Scholar
Machado, C. J. G., Pérez, J. D. and Suh, Y. J.. Commuting structure Jacobi operator for real hypersurfaces in complex two-plane Grassmannians. Acta Math. Sin. (Engl. Ser.) 31 (2015), 111–122.CrossRefGoogle Scholar
Pérez, J. D.. Lie derivatives on a real hypersurface in complex two-plane Grassmannians. Publ. Math. Debrecen. 89 (2016), 63–71.CrossRefGoogle Scholar
Pérez, J. D., Lee, H., Suh, Y. J. and Woo, C.. Real hypersurfaces in complex two-plane Grassmannians with Reeb parallel Ricci tensor in the GTW connection. Canad. Math. Bull. 59 (2016), 721–733.CrossRefGoogle Scholar
Pérez, J. D. and Suh, Y. J.. The Ricci tensor of real hypersurfaces in complex two-plane Grassmannians. J. Korean Math. Soc. 44 (2007), 211–235.CrossRefGoogle Scholar
Pérez, J. D., Suh, Y. J. and Woo, C.. Real hypersurfaces in complex two-plane Grassmannians with GTW harmonic curvature. Canad. Math. Bull. 58 (2015), 835–845.CrossRefGoogle Scholar
Semmelmann, U.. Conformal Killing forms on Riemannian manifolds. Math. Z. 245 (2003), 503–527.CrossRefGoogle Scholar
Suh, Y. J.. Real hypersurfaces of type B in complex two-plane Grassmannians. Monatsh. Math. 147 (2006), 337–355.Google Scholar
Suh, Y. J.. Real hypersurfaces in complex two-plane Grassmannians with parallel Ricci tensor. Proc. Roy. Soc. Edinburgh Sect. A 142 (2012), 1309–1324.CrossRefGoogle Scholar
Suh, Y. J.. Hypersurfaces with isometric Reeb flow in complex hyperbolic two-plane Grassmannians. Adv. in Appl. Math. 50 (2013), 645–659.CrossRefGoogle Scholar
Suh, Y. J.. Real hypersurfaces in complex two-plane Grassmannians with harmonic curvature. J. Math. Pures Appl. 100 (2013), 16–33.CrossRefGoogle Scholar
Suh, Y. J.. Real hypersurfaces in complex two-plane Grassmannians with Reeb parallel Ricci tensor. J. Geom. Phys. 64 (2013), 1–11.CrossRefGoogle Scholar
Suh, Y. J.. Real hypersurfaces in the complex hyperbolic quadrics with isometric Reeb flow. Commun. Contemp. Math. 20 (2018), 1750031, 20 pp.CrossRefGoogle Scholar
Suh, Y. J.. Generalized Killing Ricci tensor for real hypersurfaces in complex hyperbolic two-plane Grassmannians. Mediterr. J. Math. 18 (2021), Paper No. 88, 28 pp.CrossRefGoogle Scholar
Suh, Y. J.. Generalized Killing Ricci tensor for real hypersurfaces in complex two-plane Grassmannians. J. Geom. Phys. 159 (2021), 103799, 15 pp.CrossRefGoogle Scholar
Suh, Y. J.. Harmonic curvature for real hypersurfaces in complex hyperbolic two plane Grassmannians. J. Geom. Phys. 161 (2021), 103829, 22 pp.CrossRefGoogle Scholar
Suh, Y. J., Lee, H. and Kim, G. J.. Addendum to the paper ‘Real hypersurfaces in complex two-plane Grassmannians with $\xi$-invariant Ricci tensor’. J. Geom. Phys. 83 (2014), 99–103.Google Scholar
Suh, Y. J., Lee, H. and Kim, S.. Real hypersurfaces in complex two-plane Grassmannians with certain commuting condition II. Czechoslovak Math. J. 64 (2014), 133–148.Google Scholar