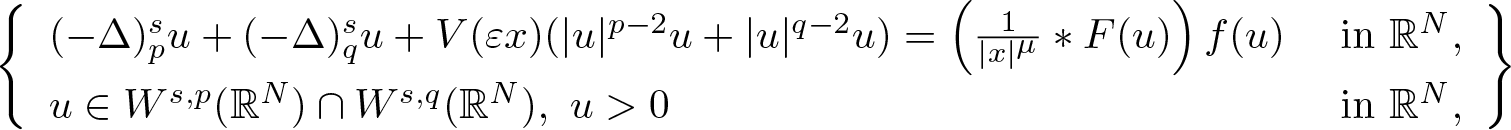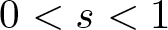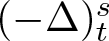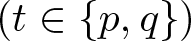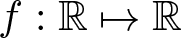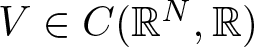1. Introduction
1.1. Features of the paper and historical comments
In this paper, we are concerned with the study of concentration and multiplicity properties of solutions for a class of fractional double phase problems with Choquard nonlinearity. The features of this paper are the following:
(i) the presence of several nonlocal operators with different growth, which generates a double phase associated energy;
(ii) the analysis developed in this paper is concerned with the combined effects of a nonstandard fractional operator with unbalanced growth and a nonlocal Choquard term;
(iii) the potential describing the absorption term satisfies a local condition and no information on the behaviour of the potential at infinity is imposed;
(iv) the main concentration property creates a bridge between the global maximum point of the solution and the global minimum of the potential;
(v) since the nonlinearity is only assumed to be continuous, one cannot apply the standard C 1-Nehari manifold arguments due to the lack of differentiability of the associated Nehari manifold;
(vi) our analysis combines the nonlocal nature of the fractional (p, q)-operator and of the Choquard nonlinearity with the local perturbation in the absorption term.
The problem studied in this paper combines both the above-mentioned features. More exactly, we are interested in concentration phenomena associated with a nonlinear Choquard problem driven by fractional Laplace operators with different power. This integro-differential operator appears in several relevant models of applied sciences. We only recall that the fractional power of the Laplace operator is the infinitesimal generator of the Lévy stable diffusion process and arises in anomalous diffusion in plasma, population dynamics, geophysical fluid dynamics, flame propagation, chemical reactions in liquids, and American options in finance. Moreover, fractional Sobolev spaces have been well known since the beginning of the last century, especially within the framework of harmonic analysis. The starting point in the study of fractional problems is attributed to the pioneering papers of Caffarelli et al. [Reference Caffarelli, Roquejoffre and Sire20–Reference Caffarelli and Silvestre22]. For a comprehensive introduction to the study of fractional equations and the use of variational methods in the treatment of these problems, we refer to the monographs by Di Nezza, Palatucci, and Valdinoci [Reference Di Nezza, Palatucci and Valdinoci27] and Molica Bisci, Rădulescu, and Servadei [Reference Molica Bisci, Rădulescu and Servadei45]. Therefore, the nonlocal operators are becoming increasingly popular in applied sciences, theoretical research, and real-world applications.
Since the content of this paper is at interplay between ‘double phase problems’ and ‘Choquard problems’, we now recall some pioneering achievements in these fields.
We start with a short description on the development of double phase problems. To the best of our knowledge, the first contributions to this field are due to the study by Ball [Reference Ball13, Reference Ball14], in relationship with problems in nonlinear elasticity and composite materials. Let ![]() $\Omega\subset\mathbb{R}^N$ be a bounded domain with a smooth boundary. If
$\Omega\subset\mathbb{R}^N$ be a bounded domain with a smooth boundary. If ![]() $u:\Omega\to\mathbb{R}^N$ is the displacement and if Du is the N × N matrix of the deformation gradient, then the total energy can be represented by an integral of the type
$u:\Omega\to\mathbb{R}^N$ is the displacement and if Du is the N × N matrix of the deformation gradient, then the total energy can be represented by an integral of the type
 \begin{equation}I(u)=\int_\varOmega f(x,\text{D}u(x))dx,\end{equation}
\begin{equation}I(u)=\int_\varOmega f(x,\text{D}u(x))dx,\end{equation} where the energy function ![]() $f=f(x,\xi):\Omega\times\mathbb{R}^{N\times N}\to\mathbb{R}$ is quasiconvex with respect to ξ, see the study by Morrey [Reference Morrey47]. A simple example considered by Ball is given by functions f of the type
$f=f(x,\xi):\Omega\times\mathbb{R}^{N\times N}\to\mathbb{R}$ is quasiconvex with respect to ξ, see the study by Morrey [Reference Morrey47]. A simple example considered by Ball is given by functions f of the type
where ![]() ${\mathrm{det}}\,\xi$ is the determinant of the N × N matrix ξ and g, h are non-negative convex functions, which satisfy the growth conditions
${\mathrm{det}}\,\xi$ is the determinant of the N × N matrix ξ and g, h are non-negative convex functions, which satisfy the growth conditions
 \begin{align*}g(\xi)\geqslant c_1\,|\xi|^p;\quad\lim_{t\to+\infty}h(t)=+\infty,\end{align*}
\begin{align*}g(\xi)\geqslant c_1\,|\xi|^p;\quad\lim_{t\to+\infty}h(t)=+\infty,\end{align*} where c 1 is a positive constant and ![]() $1 \lt p \lt N$. The condition
$1 \lt p \lt N$. The condition ![]() $p\leqslant N$ is necessary to study the existence of equilibrium solutions with cavities, that is, minima of the variational integral (1.1) that are discontinuous at one point where a cavity forms; in fact, every u with finite energy belongs to the Sobolev space
$p\leqslant N$ is necessary to study the existence of equilibrium solutions with cavities, that is, minima of the variational integral (1.1) that are discontinuous at one point where a cavity forms; in fact, every u with finite energy belongs to the Sobolev space ![]() $W^{1,p}(\Omega,\mathbb{R}^N)$, and thus it is a continuous function if p > N. In accordance with these problems arising in nonlinear elasticity, Marcellini [Reference Marcellini41, Reference Marcellini42] considered continuous functions
$W^{1,p}(\Omega,\mathbb{R}^N)$, and thus it is a continuous function if p > N. In accordance with these problems arising in nonlinear elasticity, Marcellini [Reference Marcellini41, Reference Marcellini42] considered continuous functions ![]() $f=f(x,u)$ with unbalanced growth that satisfy
$f=f(x,u)$ with unbalanced growth that satisfy
where c 1, c 2 are positive constants and ![]() $1\leqslant p\leqslant q$. Recently, a great deal of works have enriched the mathematical analysis of nonlinear models with unbalanced growth; we refer to the works of Bahrouni, Rădulescu, and Repovš [Reference Bahrouni, Rădulescu and Repovš12]; Crespo-Blanco, Gasínski, Harjulehto; and Winkert [Reference Crespo-Blanco, Gasínski, Harjulehto and Winkert23]; Liu and Papageorgiou [Reference Liu and Papageorgiou40]; and Papageorgiou, Pudełko, Rădulescu [Reference Papageorgiou, Pudełko and Rădulescu49]. In addition, an overview of recent developments on the regularity of nonlocal double problems can be found in Byun, Ok, and Kyeong [Reference Byun, Ok and Kyeong19] and De Filippis and Palatucci [Reference De Filippis and Palatucci25].
$1\leqslant p\leqslant q$. Recently, a great deal of works have enriched the mathematical analysis of nonlinear models with unbalanced growth; we refer to the works of Bahrouni, Rădulescu, and Repovš [Reference Bahrouni, Rădulescu and Repovš12]; Crespo-Blanco, Gasínski, Harjulehto; and Winkert [Reference Crespo-Blanco, Gasínski, Harjulehto and Winkert23]; Liu and Papageorgiou [Reference Liu and Papageorgiou40]; and Papageorgiou, Pudełko, Rădulescu [Reference Papageorgiou, Pudełko and Rădulescu49]. In addition, an overview of recent developments on the regularity of nonlocal double problems can be found in Byun, Ok, and Kyeong [Reference Byun, Ok and Kyeong19] and De Filippis and Palatucci [Reference De Filippis and Palatucci25].
In the pioneering works of Fröhlich [Reference Fröhlich30] and Pekar [Reference Pekar50], the following Choquard equation was introduced,
 \begin{align}
-\Delta u +u = \left(\frac{1}{|x|}* |u|^2\right) u \ \text{in}\ \mathbb{R}^3,
\end{align}
\begin{align}
-\Delta u +u = \left(\frac{1}{|x|}* |u|^2\right) u \ \text{in}\ \mathbb{R}^3,
\end{align}which models quantum polaron and corresponds to the study of the free electrons in ionic lattices interacting with phonons associated with deformations of the lattices or with the polarization created on the medium. Choquard also used it to study steady states of the one component plasma approximation in the Hartree–Fock theory describing an electron trapped in its own hole [Reference Lieb37]. Equation (1.2) is also called the Schrödinger–Newton equation which combines the Schrödinger equation of quantum physics with nonrelativistic Newtonian gravity. Such a model can also be deduced from the Einstein–Klein–Gordon and Einstein–Dirac systems related to boson stars and the collapse of galaxy fluctuations of scalar field dark matter; we bring the reader’s attention to Elgart and Schlein [Reference Elgart and Schlein29], Jones [Reference Jones36], Lions [Reference Lions39], Penrose [Reference Penrose51, Reference Penrose56], and Schunck and Mielke [Reference Schunck and Mielke54].
In conclusion, based on the historical research background of the fractional double problem and the Choquard problem and the related theoretical foundation, focusing on the characteristics of such problems and the combined effects produced by their combination, we will apply analytical, topological, and variational methods and develop some new techniques to devote ourselves to the study of new phenomena of nonlocal double problems with nonlocal reaction terms, when the potential V satisfies a general local condition and the nonlinearity f possesses only the continuity property.
1.2. Statement of the problem and main result
In this paper, we focus on the existence, multiplicity, and concentration behaviour of positive solutions for the nonlinear fractional (p, q)-Choquard problem:
 \begin{align}
\left\{
\begin{array}{lll}
(- \Delta)_p^s u + (- \Delta)_q ^s u + V(\varepsilon x) (|u|^{p - 2} u + |u|^{q - 2} u) = \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in}\ \mathbb{R}^N, \\
u \in W^{s,p}(\mathbb{R}^N) \cap W^{s,q}(\mathbb{R}^N) ,\ u \gt 0 & \ \text{in}\ \mathbb{R}^N,
\end{array}
\right\}
\end{align}
\begin{align}
\left\{
\begin{array}{lll}
(- \Delta)_p^s u + (- \Delta)_q ^s u + V(\varepsilon x) (|u|^{p - 2} u + |u|^{q - 2} u) = \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in}\ \mathbb{R}^N, \\
u \in W^{s,p}(\mathbb{R}^N) \cap W^{s,q}(\mathbb{R}^N) ,\ u \gt 0 & \ \text{in}\ \mathbb{R}^N,
\end{array}
\right\}
\end{align} where ɛ is a positive parameter, ![]() $0 \lt s \lt 1$,
$0 \lt s \lt 1$, ![]() $2 \leqslant p \lt q \lt \min\{2p, N / s\}$,
$2 \leqslant p \lt q \lt \min\{2p, N / s\}$, ![]() $0 \lt \mu \lt sp$,
$0 \lt \mu \lt sp$, ![]() $(- \Delta)_t^s$
$(- \Delta)_t^s$ ![]() $(t \in \left\{p,q\right\})$ is the fractional t-Laplace operator,
$(t \in \left\{p,q\right\})$ is the fractional t-Laplace operator, ![]() $V : \mathbb{R}^N \mapsto \mathbb{R}$ and
$V : \mathbb{R}^N \mapsto \mathbb{R}$ and ![]() $f : \mathbb{R} \mapsto \mathbb{R}$ are continuous functions, F is the primitive function of f, and
$f : \mathbb{R} \mapsto \mathbb{R}$ are continuous functions, F is the primitive function of f, and ![]() $*$ denotes the convolution product.
$*$ denotes the convolution product.
In the local setting corresponding to ![]() $s \rightarrow 1^-$ (up to normalization), the double phase problem (1.3) is motivated by numerous models arising in mathematical physics. For instance, we can refer to the following Born–Infeld equation [Reference Bonheure, d’Avenia and Pomponio16] that appears in electromagnetism:
$s \rightarrow 1^-$ (up to normalization), the double phase problem (1.3) is motivated by numerous models arising in mathematical physics. For instance, we can refer to the following Born–Infeld equation [Reference Bonheure, d’Avenia and Pomponio16] that appears in electromagnetism:
 \begin{equation*}-\mathrm{div}\,\left(\frac{\text{D}u}{(1-2\vert\text{D}u\vert^2)^{1/2}}\right)=h(u)\;\text{in}\;\varOmega.\end{equation*}
\begin{equation*}-\mathrm{div}\,\left(\frac{\text{D}u}{(1-2\vert\text{D}u\vert^2)^{1/2}}\right)=h(u)\;\text{in}\;\varOmega.\end{equation*}Indeed, by the Taylor formula, we have
 \begin{align*}(1-x)^{-1/2}=1+\frac x2+\frac{3}{2\cdot 2^2}x^2+\frac{5!!}{3!\cdot 2^3}x^3+\cdots +\frac{(2n-3)!!}{(n-1)!2^{n-1}}x^{n-1}+\cdots\ \text{for}\ |x| \lt 1.\end{align*}
\begin{align*}(1-x)^{-1/2}=1+\frac x2+\frac{3}{2\cdot 2^2}x^2+\frac{5!!}{3!\cdot 2^3}x^3+\cdots +\frac{(2n-3)!!}{(n-1)!2^{n-1}}x^{n-1}+\cdots\ \text{for}\ |x| \lt 1.\end{align*} Taking ![]() $x=2\vert\text{D}u\vert^2$ and adopting the first-order approximation, we get a particular case of the problem (1.3) for p = 2 and q = 4. Furthermore, the n-th order approximation problem is driven by the multi-phase differential operator
$x=2\vert\text{D}u\vert^2$ and adopting the first-order approximation, we get a particular case of the problem (1.3) for p = 2 and q = 4. Furthermore, the n-th order approximation problem is driven by the multi-phase differential operator
 \begin{align*}-\Delta u-\Delta_4u-\frac 32\Delta_6u-\cdots -\frac{(2n-3)!!}{(n-1)!}\Delta_{2n}u.\end{align*}
\begin{align*}-\Delta u-\Delta_4u-\frac 32\Delta_6u-\cdots -\frac{(2n-3)!!}{(n-1)!}\Delta_{2n}u.\end{align*}Finally, we also refer to the following fourth-order relativistic operator:
 \begin{align*}u \mapsto {\mathrm{div}\, }\left(\frac{|\nabla u|^2}{(1-|\nabla u|^4)^{3/4}} \nabla u\right),\end{align*}
\begin{align*}u \mapsto {\mathrm{div}\, }\left(\frac{|\nabla u|^2}{(1-|\nabla u|^4)^{3/4}} \nabla u\right),\end{align*}which describes large classes of phenomena arising in relativistic quantum mechanics. Clearly, we can use the Taylor formula to conclude that the fourth-order relativistic operator can be approximated by the following double phase operator:
 \begin{align*}u \mapsto \Delta_4 u + \frac{3}{4}\Delta_8 u.\end{align*}
\begin{align*}u \mapsto \Delta_4 u + \frac{3}{4}\Delta_8 u.\end{align*} The purpose of this paper is to study a class of fractional unbalanced double phase problems in which the nonlocal term appears also in the nonlinear part. Problem (1.3) is closely related to the analysis of nonlinear problems and stationary waves for models arising in mathematical physics, such as phase transitions, anomalous diffusion, composite materials, image processing, fractional quantum mechanics in the study of particles on stochastic fields, fractional superdiffusion, and fractional white-noise limit, see the study by Pucci and Saldi [Reference Pucci and Saldi52]. For more details, we refer interested readers to the preliminary introduction of this topic in [Reference Di Nezza, Palatucci and Valdinoci27, Reference Molica Bisci, Rădulescu and Servadei45]. From the point of view of physics, in the semi-classical sense (namely, as ![]() $ \varepsilon \rightarrow 0$), it is of great significance to study the existence and shape of the standing wave solutions of problem (1.3), which can be used to describe the transition relationship between quantum mechanics and classical mechanics. From a mathematical point of view, in the framework of this semi-classical state, we can obtain more dynamic behaviour information, such as concentration, convergence, decay, bifurcation, and other properties.
$ \varepsilon \rightarrow 0$), it is of great significance to study the existence and shape of the standing wave solutions of problem (1.3), which can be used to describe the transition relationship between quantum mechanics and classical mechanics. From a mathematical point of view, in the framework of this semi-classical state, we can obtain more dynamic behaviour information, such as concentration, convergence, decay, bifurcation, and other properties.
Note that, if ![]() $p=q=2$, after rescaling, problem (1.3) reduces to the following nonlinear fractional Choquard equation:
$p=q=2$, after rescaling, problem (1.3) reduces to the following nonlinear fractional Choquard equation:
 \begin{align}
\varepsilon^{2s}(- \Delta)^s u + V(x) u =\varepsilon^{\mu -N} \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N.
\end{align}
\begin{align}
\varepsilon^{2s}(- \Delta)^s u + V(x) u =\varepsilon^{\mu -N} \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N.
\end{align} When ɛ = 1, ![]() $F(u)=|u|^p$, and
$F(u)=|u|^p$, and ![]() $f(u)=|u|^{p-2}u$, d’Avenia, Siciliano and Squassina [Reference d’Avenia, Siciliano and Squassina24] dealt with the regularity, existence and non-existence, symmetry, and decay properties of solutions to problem (1.4). Under assumption that the potential V has a local minimum, Ambrosio [Reference Ambrosio9] established the multiplicity and concentration of positive solutions to problem (1.4) via the penalization technique and Ljusternik-Schnirelmann theory.
$f(u)=|u|^{p-2}u$, d’Avenia, Siciliano and Squassina [Reference d’Avenia, Siciliano and Squassina24] dealt with the regularity, existence and non-existence, symmetry, and decay properties of solutions to problem (1.4). Under assumption that the potential V has a local minimum, Ambrosio [Reference Ambrosio9] established the multiplicity and concentration of positive solutions to problem (1.4) via the penalization technique and Ljusternik-Schnirelmann theory.
When ![]() $p=q \neq 2$, after rescaling, problem (1.3) boils down to the following nonlinear fractional Choquard problem:
$p=q \neq 2$, after rescaling, problem (1.3) boils down to the following nonlinear fractional Choquard problem:
 \begin{align}
\left\{
\begin{array}{lll}
\varepsilon^{sp}(- \Delta)_p^s u + V(x)|u|^{p-2}u = \varepsilon^{\mu-N}\left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N, \\
u \in W^{s,p}(\mathbb{R}^N),\ u \gt 0 & \ \text{in } \mathbb{R}^N.
\end{array}
\right\}
\end{align}
\begin{align}
\left\{
\begin{array}{lll}
\varepsilon^{sp}(- \Delta)_p^s u + V(x)|u|^{p-2}u = \varepsilon^{\mu-N}\left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N, \\
u \in W^{s,p}(\mathbb{R}^N),\ u \gt 0 & \ \text{in } \mathbb{R}^N.
\end{array}
\right\}
\end{align} In [Reference Ambrosio7], Ambrosio investigated the existence, multiplicity, and concentration of positive solutions for the fractional Choquard problem (1.5) by assuming that the potential ![]() $V :\mathbb{R}^N \mapsto \mathbb{R}$ fulfills the following condition due to the study by Rabinowitz [Reference Rabinowitz53]:
$V :\mathbb{R}^N \mapsto \mathbb{R}$ fulfills the following condition due to the study by Rabinowitz [Reference Rabinowitz53]:
(V)
 $V_\infty=\liminf_{|x| \rightarrow +\infty} V(x) \gt \inf_{x\in\mathbb{R}^N}V(x)$.
$V_\infty=\liminf_{|x| \rightarrow +\infty} V(x) \gt \inf_{x\in\mathbb{R}^N}V(x)$.
These solutions concentrate at global minimum points of V under the global hypothesis (V). In the local sense s = 1, problem (1.5) becomes the following quasi-linear Choquard problem with the p-Laplace operator
 \begin{align}
\left\{
\begin{array}{lll}
- \varepsilon^{p}\Delta_p u + V(x)|u|^{p-2}u = \varepsilon^{\mu-N}\left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N, \\
u \in W^{1,p}(\mathbb{R}^N),\ u \gt 0 & \ \text{in } \mathbb{R}^N,
\end{array}
\right\}
\end{align}
\begin{align}
\left\{
\begin{array}{lll}
- \varepsilon^{p}\Delta_p u + V(x)|u|^{p-2}u = \varepsilon^{\mu-N}\left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N, \\
u \in W^{1,p}(\mathbb{R}^N),\ u \gt 0 & \ \text{in } \mathbb{R}^N,
\end{array}
\right\}
\end{align} for which several existence, multiplicity, and concentration results of positive solutions have been studied by different authors, under suitable assumptions on the potential function V and the reaction f; see, for instance, Alves and Yang [Reference Alves and Yang3–Reference Alves and Yang5]. On the other hand, if s = 1 and ![]() $1 \lt p \lt q \lt N$, after rescaling, problem (1.3) reduces to the following (p, q)-Laplace problem:
$1 \lt p \lt q \lt N$, after rescaling, problem (1.3) reduces to the following (p, q)-Laplace problem:
 \begin{align}
\left\{
\begin{array}{lll}
- \varepsilon^{p}\Delta_p u - \varepsilon^q \Delta_q u + V(x) (|u|^{p - 2} u + |u|^{q - 2} u) =\varepsilon^{\mu -N} \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N, \\
u \in W^{1,p}(\mathbb{R}^N) \cap W^{1,p}(\mathbb{R}^N) ,\ u \gt 0 & \ \text{in }\mathbb{R}^N.
\end{array}
\right\}
\end{align}
\begin{align}
\left\{
\begin{array}{lll}
- \varepsilon^{p}\Delta_p u - \varepsilon^q \Delta_q u + V(x) (|u|^{p - 2} u + |u|^{q - 2} u) =\varepsilon^{\mu -N} \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N, \\
u \in W^{1,p}(\mathbb{R}^N) \cap W^{1,p}(\mathbb{R}^N) ,\ u \gt 0 & \ \text{in }\mathbb{R}^N.
\end{array}
\right\}
\end{align}Very recently, by assuming that the potential V and the nonlinear reaction f satisfy the following conditions:
 $(\overline{V})$
$(\overline{V})$  $V \in C(\mathbb{R}^N,\mathbb{R})$ and
$V \in C(\mathbb{R}^N,\mathbb{R})$ and  $+ \infty \gt V_\infty=\liminf_{|x| \rightarrow +\infty} V(x) \gt \inf_{x\in\mathbb{R}^N}V(x) \gt 0$;
$+ \infty \gt V_\infty=\liminf_{|x| \rightarrow +\infty} V(x) \gt \inf_{x\in\mathbb{R}^N}V(x) \gt 0$;(f)
 $~~f \in C^1(\mathbb{R},\mathbb{R})$,
$~~f \in C^1(\mathbb{R},\mathbb{R})$,
Zhang, Zhang, and Rădulescu studied the multiplicity and concentration behavior of positive solutions to problem (1.7) in [Reference Zhang, Zhang and Rădulescu60].
For related concentration and multiplicity properties of solutions, we refer to the recent paper by Alves and de Morais Filho [Reference Alves and de Morais Filho2]; Alves, Ambrosio, and Isernia [Reference Alves, Ambrosio and Isernia1]; Ambrosio [Reference Ambrosio8]; Ambrosio, Isernia, and Rădulescu [Reference Ambrosio, Isernia and Rădulescu10]; Ambrosio and Rădulescu [Reference Ambrosio and Rădulescu11]; Del Pino and Felmer [Reference Del Pino and Felmer26]; Gao, Tang, and Chen [Reference Gao, Tang and Chen31]; Gu and Tang [Reference Gu and Tang32]; Ji and Rădulescu [Reference Ji and Rădulescu34, Reference Ji and Rădulescu35]; Moroz and Van Schaftingen [Reference Moroz and Van Schaftingen46]; Zhang and Zhang [Reference Zhang and Zhang61]; Zhang, Zhang, and Rădulescu [Reference Zhang, Zhang and Rădulescu59]; and Zhang, Tang, and Rădulescu [Reference Zhang, Tang and Rădulescu62]. We also cite the study by Mingione and Rădulescu [Reference Mingione and Rădulescu44] for an overview of recent results concerning elliptic variational problems with nonstandard growth and nonuniform ellipticity.
Inspired by the above works, in this paper, we are interested in studying the multiplicity and concentration behaviour as ![]() $\varepsilon \rightarrow 0$ of positive solutions for problem (1.3), when we suppose a local condition on the potential V, and the nonlinear term f is only assumed to be continuous (without C 1 differentiability). Precisely, we first impose that V is a continuous map satisfying the following assumptions:
$\varepsilon \rightarrow 0$ of positive solutions for problem (1.3), when we suppose a local condition on the potential V, and the nonlinear term f is only assumed to be continuous (without C 1 differentiability). Precisely, we first impose that V is a continuous map satisfying the following assumptions:
there exists
 $V_0 \gt 0$ such that
$V_0 \gt 0$ such that  $V_0 := \inf_{x \in \mathbb{R}^N} V(x)$;
$V_0 := \inf_{x \in \mathbb{R}^N} V(x)$;there exists an open bounded domain
 $\Lambda \subset \mathbb{R}^N$ such that
$\Lambda \subset \mathbb{R}^N$ such that
 \begin{align*}V_0 \lt \min_{\partial \Lambda}V\quad \ \text{and }\quad M :=\{x \in \Lambda : V(x) = V_0\} \neq \emptyset.\end{align*}
\begin{align*}V_0 \lt \min_{\partial \Lambda}V\quad \ \text{and }\quad M :=\{x \in \Lambda : V(x) = V_0\} \neq \emptyset.\end{align*}
Next, we assume that f is a merely continuous function that verifies the following conditions:
(f1)
 $\lim_{t \rightarrow 0} \frac{|f(t)|}{|t|^{p - 1}} = 0$;
$\lim_{t \rightarrow 0} \frac{|f(t)|}{|t|^{p - 1}} = 0$;(f2) there exists
 $\nu \in (q, q_s^*(2 - \mu / N) / 2)$ such that
$\nu \in (q, q_s^*(2 - \mu / N) / 2)$ such that
 \begin{align*}\lim_{|t| \rightarrow + \infty} \frac{|f(t)|}{|t|^{\nu - 1}} = 0,\end{align*}
\begin{align*}\lim_{|t| \rightarrow + \infty} \frac{|f(t)|}{|t|^{\nu - 1}} = 0,\end{align*}where
 $q_s^* = Nq / (N - sq)$;
$q_s^* = Nq / (N - sq)$;(f3)
 $0 \lt p F(t) : = p \int^t_0 f(\tau) d\tau \leqslant f(t)t$ for all t > 0;
$0 \lt p F(t) : = p \int^t_0 f(\tau) d\tau \leqslant f(t)t$ for all t > 0;(f4) the map
 $t \mapsto \frac{f(t)}{t^{q - 1}}$ is increasing for all t > 0.
$t \mapsto \frac{f(t)}{t^{q - 1}}$ is increasing for all t > 0.
Remark 1.1. We would like to point out that, since the hypotheses on V and f are different from [Reference Ambrosio7, Reference Rabinowitz53, Reference Zhang, Zhang and Rădulescu59–Reference Zhang and Zhang61], our arguments are totally distinct with them and improve the previous results for the singularly perturbed fractional problem with nonlocal Choquard reaction, in the sense that we establish multiplicity results and concentration behaviour for the fractional (p, q)-problems involving continuous nonlinearity and by imposing a local condition on the potential V. Compared with the local case s =1, we point out that our result improves theorem 1.2 in [Reference Zhang, Zhang and Rădulescu60]. In addition, we believe that the ideas contained here can be used in other cases to study problems driven by more general operators, under local conditions on the potential V and without the differentiability of the nonlinearity f.
In order to look for positive solutions of problem (1.3), we may assume that ![]() $f(t) = 0$ for all
$f(t) = 0$ for all ![]() $t \leqslant 0$.
$t \leqslant 0$.
Recall that if A is a closed subset of a topological space Y, then we use ![]() ${\mathrm{cat}}_Y(A)$ to denote the Ljusternik–Schnirelmann category of A in Y, that is, the smallest number of closed and contractible sets in Y which cover A. For more details, we refer to the study by Willem [Reference Willem57].
${\mathrm{cat}}_Y(A)$ to denote the Ljusternik–Schnirelmann category of A in Y, that is, the smallest number of closed and contractible sets in Y which cover A. For more details, we refer to the study by Willem [Reference Willem57].
Our main result in this paper establishes the following concentration and multiplicity properties.
Theorem 1.2 Let ![]() $0 \lt \mu \lt sp.$ Assume that the nonlinearity f fulfils
$0 \lt \mu \lt sp.$ Assume that the nonlinearity f fulfils ![]() $(f_1)$–
$(f_1)$–![]() $(f_4)$ with
$(f_4)$ with ![]() $\nu \lt (N - \mu) q / (N - sq)$ and the potential V verifies hypotheses
$\nu \lt (N - \mu) q / (N - sq)$ and the potential V verifies hypotheses ![]() $(V_1)$–
$(V_1)$–![]() $(V_2).$ Then for all δ > 0 such that
$(V_2).$ Then for all δ > 0 such that ![]() $M_\delta :=\left\{x \in \mathbb{R}^N : {\mathrm{dist}\,}(x,M) \leqslant \delta\right\} \subset \Lambda,$ there exists
$M_\delta :=\left\{x \in \mathbb{R}^N : {\mathrm{dist}\,}(x,M) \leqslant \delta\right\} \subset \Lambda,$ there exists ![]() $\varepsilon_\delta \gt 0$ such that, for any
$\varepsilon_\delta \gt 0$ such that, for any ![]() $\varepsilon \in (0,\varepsilon_\delta)$ problem (1.3) has at least
$\varepsilon \in (0,\varepsilon_\delta)$ problem (1.3) has at least ![]() $cat_{M_\delta}(M)$ positive solutions. Moreover, if uɛ denotes one of these solutions and
$cat_{M_\delta}(M)$ positive solutions. Moreover, if uɛ denotes one of these solutions and ![]() $x_\varepsilon \in \mathbb{R}^N$ is the global maximum point of
$x_\varepsilon \in \mathbb{R}^N$ is the global maximum point of ![]() $u_\varepsilon,$ then
$u_\varepsilon,$ then ![]() $\lim_{\varepsilon \rightarrow 0} V(\varepsilon x_\varepsilon) = V_0.$
$\lim_{\varepsilon \rightarrow 0} V(\varepsilon x_\varepsilon) = V_0.$
The proof of theorem 1.2 is based on topological and variational methods and refined analytic techniques. Let us now take the next steps to outline our strategies and methods for proving theorem 1.2:
(1) concerning our variational approach: because there is no information on the behaviour of V at infinity, as in [Reference Del Pino and Felmer26], we first modify in a convenient way the nonlinear reaction outside the set Λ, and then we will study an auxiliary problem. The main characteristic of the corresponding modified energy functional is that it verifies all the conditions of the mountain pass theorem [Reference Ambrosetti and Rabinowitz6]. Finally, we prove that, for ɛ > 0 sufficiently small, the solutions of the auxiliary problem are indeed solutions of the original one;
(2) topological techniques: in order to get multiple solutions of the auxiliary problem, we will use the generalized Neahri manifold method and some well-known topological techniques proposed by Benci and Cerami in [Reference Benci and Cerami15] based on accurate comparisons between the category of some sub-level sets of the modified functional and the category of the set M. Note that the nonlinearity is only continuous, and we stress that standard C 1-Nehari manifold arguments as in [Reference Zhang, Zhang and Rădulescu60] cannot be employed in our setting due to the lack of differentiability of the associated Nehari manifold. To this end, we take inspiration by some ideas developed in [Reference Szulkin, Weth, Gao and Motreanu55] and make use of some abstract critical point results obtained in [Reference Szulkin, Weth, Gao and Motreanu55] to overcome this obstacle;
(3) the combination effects of nonlocality and nonhomogeneous: the lack of homogeneity caused by fractional (p, q)-Laplacian operator, together with the appearance of nonlocal Choquard reaction term, makes our analysis more refined and interesting than the above works and also brings some new difficulties to our analysis. In particular, we need to develop a suitable Moser iteration scheme to obtain ![]() $L^\infty$-estimates and absorb some ideas from [Reference Ambrosio and Rădulescu11, Reference Zhang, Tang and Rădulescu62] to build on the Hölder regularity results under this work.
$L^\infty$-estimates and absorb some ideas from [Reference Ambrosio and Rădulescu11, Reference Zhang, Tang and Rădulescu62] to build on the Hölder regularity results under this work.
Throughout this paper, C, C 0, C 1, C 2, ... denote positive constants whose exact values are inessential and can change from line to line, and the same C, C 0, C 1, C 2, ... may represent different constants; ![]() $B_\rho(y)$ denotes the open ball centred at
$B_\rho(y)$ denotes the open ball centred at ![]() $y \in \mathbb{R}^N$ with radius ρ > 0, and
$y \in \mathbb{R}^N$ with radius ρ > 0, and ![]() $B_\rho^c(y)$ denotes the complement of
$B_\rho^c(y)$ denotes the complement of ![]() $B_\rho(y)$ in
$B_\rho(y)$ in ![]() $\mathbb{R}^N$. In particular, Bρ and
$\mathbb{R}^N$. In particular, Bρ and ![]() $B_\rho^c$ denote
$B_\rho^c$ denote ![]() $B_\rho(0)$ and
$B_\rho(0)$ and ![]() $B_\rho^c(0)$, respectively.
$B_\rho^c(0)$, respectively.
2. Auxiliary results
2.1. Notations
Let ![]() $u : \mathbb{R}^N \mapsto \mathbb{R}$. For
$u : \mathbb{R}^N \mapsto \mathbb{R}$. For ![]() $0 \lt s \lt 1$ and p > 1, we define the fractional Sobolev space
$0 \lt s \lt 1$ and p > 1, we define the fractional Sobolev space
 \begin{align*}W^{s,p}(\mathbb{R}^N) & := \left\{u : |u|_p^p := \int_{\mathbb{R}^N} |u|^p dx \lt + \infty,\ [u]_{s,p}^p \right.\\
& \quad \left. := \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u(x) - u(y)|^p}{|x - y|^{N + sp}} dxdy \lt + \infty\right\}\end{align*}
\begin{align*}W^{s,p}(\mathbb{R}^N) & := \left\{u : |u|_p^p := \int_{\mathbb{R}^N} |u|^p dx \lt + \infty,\ [u]_{s,p}^p \right.\\
& \quad \left. := \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u(x) - u(y)|^p}{|x - y|^{N + sp}} dxdy \lt + \infty\right\}\end{align*}equipped with the natural norm
 \begin{align*}\|u\|_{W^{s,p}(\mathbb{R}^N)} := \left([u]_{s,p}^p + |u|_p^p\right)^{\frac{1}{p}}.\end{align*}
\begin{align*}\|u\|_{W^{s,p}(\mathbb{R}^N)} := \left([u]_{s,p}^p + |u|_p^p\right)^{\frac{1}{p}}.\end{align*} For all u, ![]() $v \in W^{s,p}(\mathbb{R}^N)$, we define
$v \in W^{s,p}(\mathbb{R}^N)$, we define
 \begin{align*}\langle u, v \rangle_{s,p} := \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u(x) - u(y)|^{p - 2} (u(x) - u(y)) (v(x) - v(y))}{|x - y|^{N + sp}} dxdy.\end{align*}
\begin{align*}\langle u, v \rangle_{s,p} := \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u(x) - u(y)|^{p - 2} (u(x) - u(y)) (v(x) - v(y))}{|x - y|^{N + sp}} dxdy.\end{align*} We now recall some fundamental embeddings. Let ![]() $s \in (0,1)$ and
$s \in (0,1)$ and ![]() $p \in (1, + \infty)$ such that N > sp. Then for any
$p \in (1, + \infty)$ such that N > sp. Then for any ![]() $r \in [p,p_s^*]$ there exists a constant such that
$r \in [p,p_s^*]$ there exists a constant such that ![]() $C_r \gt 0$ such that
$C_r \gt 0$ such that
 \begin{align}
|u|_r \leqslant C_r \|u\|_{W^{s,p}(\mathbb{R}^N)}
\end{align}
\begin{align}
|u|_r \leqslant C_r \|u\|_{W^{s,p}(\mathbb{R}^N)}
\end{align} for all ![]() $u \in W^{s,p}(\mathbb{R}^N)$. Moreover,
$u \in W^{s,p}(\mathbb{R}^N)$. Moreover, ![]() $W^{s,p}(\mathbb{R}^N)$ is compactly embedded in
$W^{s,p}(\mathbb{R}^N)$ is compactly embedded in ![]() $L^r_{\mathrm{loc}}(\mathbb{R}^N)$ for any
$L^r_{\mathrm{loc}}(\mathbb{R}^N)$ for any ![]() $r \in [1,p_s^*)$.
$r \in [1,p_s^*)$.
In order to treat the nonlinear fractional (p, q)-Choquard problem, we use the following space:
endowed with the norm
 \begin{align*}\|u\|_X := \|u\|_{W^{s,p}(\mathbb{R}^N)} + \|u\|_{W^{s,q}(\mathbb{R}^N)}.\end{align*}
\begin{align*}\|u\|_X := \|u\|_{W^{s,p}(\mathbb{R}^N)} + \|u\|_{W^{s,q}(\mathbb{R}^N)}.\end{align*} Additionally, since ![]() $W^{s,r}(\mathbb{R}^N)$ (
$W^{s,r}(\mathbb{R}^N)$ (![]() $1 \lt r \lt + \infty$) is a separable reflexive Banach space, then X is also a separable reflexive Banach space.
$1 \lt r \lt + \infty$) is a separable reflexive Banach space, then X is also a separable reflexive Banach space.
2.2. The penalized problem
In order to overcome the lack of compactness of problem (1.3), we shall adapt the penalization method introduced by del Pino and Felmer [Reference Del Pino and Felmer26] to deal with the nonlinear fractional (p, q)-Choquard problem. Furthermore, without loss of generality, we can assume that
So, we need to find a constant K > 0 (which is determined later, see lemma 2.6) and take a unique number a > 0 such that  $f(a) = \frac{V_0}{K} \left(a^{p - 1} + a^{q - 1}\right)$.
$f(a) = \frac{V_0}{K} \left(a^{p - 1} + a^{q - 1}\right)$.
Now, we define
 \begin{align*}
\widetilde{f}(t) =
\begin{cases}
\ f(t), & \ \text{if } t \leqslant a,\\
\ \frac{V_0}{K} \left( t^{p - 1} + t^{q - 1} \right), & \ \text{if } t \gt a
\end{cases}
\end{align*}
\begin{align*}
\widetilde{f}(t) =
\begin{cases}
\ f(t), & \ \text{if } t \leqslant a,\\
\ \frac{V_0}{K} \left( t^{p - 1} + t^{q - 1} \right), & \ \text{if } t \gt a
\end{cases}
\end{align*}and
 \begin{align*}
g(x,t) =
\begin{cases}
\ \chi_\Lambda (x) f(t) + (1 - \chi_\Lambda(x)) \widetilde{f}(t), & \ \text{if } t \gt 0,\\
\ 0, & \ \text{if } t \leqslant 0,
\end{cases}
\end{align*}
\begin{align*}
g(x,t) =
\begin{cases}
\ \chi_\Lambda (x) f(t) + (1 - \chi_\Lambda(x)) \widetilde{f}(t), & \ \text{if } t \gt 0,\\
\ 0, & \ \text{if } t \leqslant 0,
\end{cases}
\end{align*} where ![]() $\chi_\Omega$ is the characteristic function on
$\chi_\Omega$ is the characteristic function on ![]() $\Omega \subset \mathbb{R}^N$.
$\Omega \subset \mathbb{R}^N$.
We can easily observe that g is a Carathéodory function and fulfills the following properties:
(g1)
 $\lim_{t \rightarrow 0^+} \frac{g(x,t)}{t^{p - 1}} = 0$ uniformly for all
$\lim_{t \rightarrow 0^+} \frac{g(x,t)}{t^{p - 1}} = 0$ uniformly for all  $x \in \mathbb{R}^N$;
$x \in \mathbb{R}^N$;(g2)
 $g(x,t) \leqslant f(t)$ for all
$g(x,t) \leqslant f(t)$ for all  $x \in \mathbb{R}^N$ and t > 0;
$x \in \mathbb{R}^N$ and t > 0;(g3)i
 $0 \lt p G(x,t) := p \int^t_0 g(x,\tau) d\tau \leqslant g(x,t) t$ for all
$0 \lt p G(x,t) := p \int^t_0 g(x,\tau) d\tau \leqslant g(x,t) t$ for all  $x \in \Lambda$ and t > 0;
$x \in \Lambda$ and t > 0;(g3)ii
 $0 \lt p G(x,t) \leqslant g(x,t) t \leqslant \frac{V_0}{K} \left(t^p + t^q\right)$ for all
$0 \lt p G(x,t) \leqslant g(x,t) t \leqslant \frac{V_0}{K} \left(t^p + t^q\right)$ for all  $x \in \Lambda^c$ and t > 0;
$x \in \Lambda^c$ and t > 0;(g4) the maps
 $t \mapsto \frac{g(x,t)}{t^{\frac{q}{2} - 1}}$ and
$t \mapsto \frac{g(x,t)}{t^{\frac{q}{2} - 1}}$ and  $t \mapsto \frac{G(x,t)}{t^\frac{q}{2}}$ are both increasing for all
$t \mapsto \frac{G(x,t)}{t^\frac{q}{2}}$ are both increasing for all  $x \in \mathbb{R}^N$ and t > 0.
$x \in \mathbb{R}^N$ and t > 0.
Remark 2.1. We shall consider the following penalized problem:
 \begin{align}
\left\{
\begin{array}{lll}
(- \Delta)_p^s u + (- \Delta)_q ^s u + V(\varepsilon x) (|u|^{p - 2} u + |u|^{q - 2} u) = \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right) g(\varepsilon x, u),\\
u \in X,\ u \gt 0
\end{array}
\right\}
\end{align}
\begin{align}
\left\{
\begin{array}{lll}
(- \Delta)_p^s u + (- \Delta)_q ^s u + V(\varepsilon x) (|u|^{p - 2} u + |u|^{q - 2} u) = \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right) g(\varepsilon x, u),\\
u \in X,\ u \gt 0
\end{array}
\right\}
\end{align} in ![]() $\mathbb{R}^N.$ If uɛ is a solution of problem (2.2) such that
$\mathbb{R}^N.$ If uɛ is a solution of problem (2.2) such that ![]() $u_\varepsilon(x) \leqslant a$ for all
$u_\varepsilon(x) \leqslant a$ for all ![]() $x \in \Lambda_\varepsilon^c,$ where
$x \in \Lambda_\varepsilon^c,$ where ![]() $\Lambda_\varepsilon:=\left\{x \in \mathbb{R}^N : \varepsilon x \in \Lambda \right\},$ then
$\Lambda_\varepsilon:=\left\{x \in \mathbb{R}^N : \varepsilon x \in \Lambda \right\},$ then ![]() $g(\varepsilon x, u_\varepsilon) = f(u_\varepsilon),$
$g(\varepsilon x, u_\varepsilon) = f(u_\varepsilon),$ ![]() $G(\varepsilon x, u_\varepsilon) = F(\varepsilon x,u_\varepsilon).$ So, uɛ is also a solution of problem (1.3).
$G(\varepsilon x, u_\varepsilon) = F(\varepsilon x,u_\varepsilon).$ So, uɛ is also a solution of problem (1.3).
For any ![]() $\varepsilon \geqslant 0$, we define the space
$\varepsilon \geqslant 0$, we define the space
 \begin{align*}X_\varepsilon := \left\{u \in X : \int_{\mathbb{R}^N} V(\varepsilon x)\left(|u|^p + |u|^q\right) dx \lt + \infty\right\}\end{align*}
\begin{align*}X_\varepsilon := \left\{u \in X : \int_{\mathbb{R}^N} V(\varepsilon x)\left(|u|^p + |u|^q\right) dx \lt + \infty\right\}\end{align*}equipped with the norm
where  $\|u\|_{V_\varepsilon,t}^t := [u]_{s,t}^t + \int_{\mathbb{R}^N} V(\varepsilon x) |u|^t dx$ for
$\|u\|_{V_\varepsilon,t}^t := [u]_{s,t}^t + \int_{\mathbb{R}^N} V(\varepsilon x) |u|^t dx$ for ![]() $t \in \left\{p,q\right\}$.
$t \in \left\{p,q\right\}$.
From now on, we focus on the critical points of the Euler–Lagrange functional ![]() $J_\varepsilon : {X_\varepsilon} \mapsto \mathbb{R}$ defined by
$J_\varepsilon : {X_\varepsilon} \mapsto \mathbb{R}$ defined by
 \begin{align*}J_\varepsilon(u) := \frac{1}{p} \|u\|_{V_\varepsilon,p}^p + \frac{1}{q} \|u\|_{V_\varepsilon,q}^q - \frac{1}{2} \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right)G(\varepsilon x, u) dx\end{align*}
\begin{align*}J_\varepsilon(u) := \frac{1}{p} \|u\|_{V_\varepsilon,p}^p + \frac{1}{q} \|u\|_{V_\varepsilon,q}^q - \frac{1}{2} \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right)G(\varepsilon x, u) dx\end{align*} for all ![]() $u \in {X_\varepsilon}$. By a standard argument, we can infer that
$u \in {X_\varepsilon}$. By a standard argument, we can infer that ![]() $J_\varepsilon \in C^1({X_\varepsilon},\mathbb{R})$ and its derivative is given by
$J_\varepsilon \in C^1({X_\varepsilon},\mathbb{R})$ and its derivative is given by
 \begin{align*}
\langle J_\varepsilon'(u),v \rangle & = \langle u,v \rangle_{s,p} + \langle u,v \rangle_{s,q} + \int_{\mathbb{R}^N} V(\varepsilon x)\left(|u|^{p -2} u + |u|^{q -2} u \right) vdx\\
& - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right)g(\varepsilon x, u) v dx \ \text{for all } u,\ v \in {X_\varepsilon}.
\end{align*}
\begin{align*}
\langle J_\varepsilon'(u),v \rangle & = \langle u,v \rangle_{s,p} + \langle u,v \rangle_{s,q} + \int_{\mathbb{R}^N} V(\varepsilon x)\left(|u|^{p -2} u + |u|^{q -2} u \right) vdx\\
& - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right)g(\varepsilon x, u) v dx \ \text{for all } u,\ v \in {X_\varepsilon}.
\end{align*}Let us define the Nehari manifold associated with problem (2.2), that is,
We use ![]() ${X_\varepsilon^+}$ to denote the open set defined by
${X_\varepsilon^+}$ to denote the open set defined by
and we introduce the set ![]() $S_\varepsilon^+ := S_\varepsilon \cap {X_\varepsilon^+}$, where
$S_\varepsilon^+ := S_\varepsilon \cap {X_\varepsilon^+}$, where ![]() $S_\varepsilon : = \left\{u \in {X_\varepsilon} : \|u\|_{X_\varepsilon} = 1\right\}$. We first observe that
$S_\varepsilon : = \left\{u \in {X_\varepsilon} : \|u\|_{X_\varepsilon} = 1\right\}$. We first observe that ![]() $S_\varepsilon^+$ is an incomplete
$S_\varepsilon^+$ is an incomplete ![]() $C^{1,1}$-manifold of codimension one. So, for all
$C^{1,1}$-manifold of codimension one. So, for all ![]() $u \in S_\varepsilon^+$ we have
$u \in S_\varepsilon^+$ we have ![]() $X_\varepsilon = T_u (S_\varepsilon^+) \bigoplus \mathbb{R} u$, where
$X_\varepsilon = T_u (S_\varepsilon^+) \bigoplus \mathbb{R} u$, where
 \begin{align*}
T_u (S_\varepsilon^+) := \left\{v \in {X_\varepsilon} : \langle u, v \rangle_{s,p} + \langle u, v \rangle_{s,q} + \int_{\mathbb{R}^N} V(\varepsilon x) \left(|u|^{p - 2} u + |u|^{q - 2} u\right) v dx= 0 \right\}.
\end{align*}
\begin{align*}
T_u (S_\varepsilon^+) := \left\{v \in {X_\varepsilon} : \langle u, v \rangle_{s,p} + \langle u, v \rangle_{s,q} + \int_{\mathbb{R}^N} V(\varepsilon x) \left(|u|^{p - 2} u + |u|^{q - 2} u\right) v dx= 0 \right\}.
\end{align*} Due to the fact that f is only continuous, the following result is crucial to bypass the non-differentiability of ![]() $\mathcal{N}_\varepsilon$.
$\mathcal{N}_\varepsilon$.
Lemma 2.2. Assume that ![]() $(f_1)$–
$(f_1)$–![]() $(f_4)$ and
$(f_4)$ and ![]() $(V_1)$–
$(V_1)$–![]() $(V_2)$ are fulfilled. Then the following properties hold true:
$(V_2)$ are fulfilled. Then the following properties hold true:
(a) for all
 $u \in {X_\varepsilon^+},$ there exists a unique
$u \in {X_\varepsilon^+},$ there exists a unique  $t_u \gt 0$ such that
$t_u \gt 0$ such that  $t_u u \in \mathcal{N}_\varepsilon.$ Furthermore,
$t_u u \in \mathcal{N}_\varepsilon.$ Furthermore,  $\hat{m}_\varepsilon(u) = t_u u$ is the unique maximum of
$\hat{m}_\varepsilon(u) = t_u u$ is the unique maximum of  $\ell_u(t) :=J_\varepsilon(t u);$
$\ell_u(t) :=J_\varepsilon(t u);$(b) there exists τ > 0 independent of u such that
 $t_u \geqslant \tau$ for all
$t_u \geqslant \tau$ for all  $u \in S_\varepsilon^+.$ Moreover, for each compact set
$u \in S_\varepsilon^+.$ Moreover, for each compact set  $\mathcal{W} \subset S_\varepsilon^+,$ there exists a constant
$\mathcal{W} \subset S_\varepsilon^+,$ there exists a constant  $C_\mathcal{W} \gt 0$ such that
$C_\mathcal{W} \gt 0$ such that  $t_u \leqslant C_\mathcal{W}$ for all
$t_u \leqslant C_\mathcal{W}$ for all  $u \in \mathcal{W};$
$u \in \mathcal{W};$(c) the mapping
 $\hat{m}_\varepsilon : {X_\varepsilon^+} \mapsto \mathcal{N}_\varepsilon$ is continuous and
$\hat{m}_\varepsilon : {X_\varepsilon^+} \mapsto \mathcal{N}_\varepsilon$ is continuous and  $m_\varepsilon :=\hat{m}_\varepsilon |_{S_\varepsilon^+}$ is a homeomorphism between
$m_\varepsilon :=\hat{m}_\varepsilon |_{S_\varepsilon^+}$ is a homeomorphism between  $S_\varepsilon^+$ and
$S_\varepsilon^+$ and  $\mathcal{N}_\varepsilon,$ and the inverse of mɛ is given by
$\mathcal{N}_\varepsilon,$ and the inverse of mɛ is given by  $m_\varepsilon^{-1}(u) := u / \|u\|_{X_\varepsilon};$
$m_\varepsilon^{-1}(u) := u / \|u\|_{X_\varepsilon};$(d)
 $c_\varepsilon : = \inf_{u \in \mathcal{N}_\varepsilon} J_\varepsilon(u) \geqslant \varrho_0 \gt 0$ and Jɛ is bounded below
$c_\varepsilon : = \inf_{u \in \mathcal{N}_\varepsilon} J_\varepsilon(u) \geqslant \varrho_0 \gt 0$ and Jɛ is bounded below  $\mathcal{N}_\varepsilon,$ where ϱ 0 is independent of
$\mathcal{N}_\varepsilon,$ where ϱ 0 is independent of  $\varepsilon,$ K, and
$\varepsilon,$ K, and  $a;$
$a;$(e) let
 $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and  $\nu \lt (N - \mu) q / (N - sq).$ If there exists a sequence
$\nu \lt (N - \mu) q / (N - sq).$ If there exists a sequence  $\left\{u_n\right\}_{n \in \mathbb{N}} \subset S_\varepsilon^+$ such that
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset S_\varepsilon^+$ such that  ${\mathrm{dist}\,}(u_n,\partial S_\varepsilon^+) \rightarrow 0$ as
${\mathrm{dist}\,}(u_n,\partial S_\varepsilon^+) \rightarrow 0$ as  $n \rightarrow \infty,$ then
$n \rightarrow \infty,$ then  $\|m_\varepsilon(u_n)\|_{X_\varepsilon} \rightarrow + \infty$ and
$\|m_\varepsilon(u_n)\|_{X_\varepsilon} \rightarrow + \infty$ and  $J_\varepsilon(m_\varepsilon(u_n)) \rightarrow + \infty$ as
$J_\varepsilon(m_\varepsilon(u_n)) \rightarrow + \infty$ as  $n \rightarrow \infty.$
$n \rightarrow \infty.$
Proof. (a) For each ![]() $u \in {X_\varepsilon^+}$ and t > 0,
$u \in {X_\varepsilon^+}$ and t > 0, ![]() $\ell_u(0) = 0$. From theorem 4.3 of Lieb and Loss [Reference Lieb and Loss38],
$\ell_u(0) = 0$. From theorem 4.3 of Lieb and Loss [Reference Lieb and Loss38], ![]() $(g_2)$,
$(g_2)$, ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, (2.1), and hypothesis
$(f_2)$, (2.1), and hypothesis ![]() $(V_1)$ we can deduce that there exists some constant C > 0 such that
$(V_1)$ we can deduce that there exists some constant C > 0 such that
 \begin{align*}\ell_u(t) \geqslant \frac{1}{2^{q - 1}q} \|u\|_{X_\varepsilon}^q t^q - C \|u\|_{X_\varepsilon}^{2 p }t^{2 p}\ \text{for}\ 0 \lt t \lt \frac{1}{\|u\|_{X_\varepsilon}}.\end{align*}
\begin{align*}\ell_u(t) \geqslant \frac{1}{2^{q - 1}q} \|u\|_{X_\varepsilon}^q t^q - C \|u\|_{X_\varepsilon}^{2 p }t^{2 p}\ \text{for}\ 0 \lt t \lt \frac{1}{\|u\|_{X_\varepsilon}}.\end{align*} Due to ![]() $2p \gt q$, we see that
$2p \gt q$, we see that ![]() $\ell_u(t) \gt 0$ for t > 0 sufficiently small. Using
$\ell_u(t) \gt 0$ for t > 0 sufficiently small. Using ![]() $(g_3)_i$ and
$(g_3)_i$ and ![]() $(g_3)_{ii}$, we can find a constant
$(g_3)_{ii}$, we can find a constant
 \begin{align*}C_u = \frac{1}{2} \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right)G(\varepsilon x, u) dx \gt 0\end{align*}
\begin{align*}C_u = \frac{1}{2} \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right)G(\varepsilon x, u) dx \gt 0\end{align*}such that
 \begin{align*}\ell_u(t) \leqslant \frac{1}{p} \left(\|u\|_{X_\varepsilon}^p + \|u\|_{X_\varepsilon}^q\right)t^q - C_u t^{2p}\end{align*}
\begin{align*}\ell_u(t) \leqslant \frac{1}{p} \left(\|u\|_{X_\varepsilon}^p + \|u\|_{X_\varepsilon}^q\right)t^q - C_u t^{2p}\end{align*} for all t > 1. Applying ![]() $2p \gt q$ again, we know that
$2p \gt q$ again, we know that ![]() $\ell_u(t) \lt 0$ for t > 1 large enough. Hence,
$\ell_u(t) \lt 0$ for t > 1 large enough. Hence, ![]() $\max_{t \geqslant 0} \ell_u(t)$ is attained at some
$\max_{t \geqslant 0} \ell_u(t)$ is attained at some ![]() $t_u \gt 0$ verifying
$t_u \gt 0$ verifying ![]() $\ell_u'(t_u)= 0$ and
$\ell_u'(t_u)= 0$ and ![]() $t_u u \in \mathcal{N}_\varepsilon$. We point out that
$t_u u \in \mathcal{N}_\varepsilon$. We point out that
 \begin{align}
t u \in \mathcal{N}_\varepsilon \Longleftrightarrow \|u\|^q_{V_\varepsilon,q} = \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{G(\varepsilon y, t u(y))}{t^{\frac{q}{2}} |x - y|^\mu} \frac{g(\varepsilon x, t u (x))}{t^{\frac{q}{2} - 1}} u(x) dxdy - t^{p - q} \|u\|^p_{V_\varepsilon,p}.
\end{align}
\begin{align}
t u \in \mathcal{N}_\varepsilon \Longleftrightarrow \|u\|^q_{V_\varepsilon,q} = \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{G(\varepsilon y, t u(y))}{t^{\frac{q}{2}} |x - y|^\mu} \frac{g(\varepsilon x, t u (x))}{t^{\frac{q}{2} - 1}} u(x) dxdy - t^{p - q} \|u\|^p_{V_\varepsilon,p}.
\end{align} According to q > p and ![]() $(g_4)$, we conclude that the right-hand side in (2.3) is an increasing function with respect to t > 0. Therefore, the uniqueness of tu is now obvious.
$(g_4)$, we conclude that the right-hand side in (2.3) is an increasing function with respect to t > 0. Therefore, the uniqueness of tu is now obvious.
(b) For any ![]() $u \in S_\varepsilon^+$, in view of lemma 2.2-(a), there exists
$u \in S_\varepsilon^+$, in view of lemma 2.2-(a), there exists ![]() $t_u \gt 0$ such that
$t_u \gt 0$ such that
 \begin{align*}t_u^p \|u\|_{V_\varepsilon,p}^p + t_u^q \|u\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, t_u u) \right) g(\varepsilon x, t_u u) t_u u dx.\end{align*}
\begin{align*}t_u^p \|u\|_{V_\varepsilon,p}^p + t_u^q \|u\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, t_u u) \right) g(\varepsilon x, t_u u) t_u u dx.\end{align*} By theorem 4.3 of Lieb and Loss [Reference Lieb and Loss38], together with ![]() $(g_2)$,
$(g_2)$, ![]() $(f_1)$,
$(f_1)$, ![]() $(f_2)$, (2.1), and hypothesis
$(f_2)$, (2.1), and hypothesis ![]() $(V_1)$, we can infer that for any σ > 0, there exists some constant
$(V_1)$, we can infer that for any σ > 0, there exists some constant ![]() $C_\sigma \gt 0$ such that for all
$C_\sigma \gt 0$ such that for all ![]() $u \in S_\varepsilon^+$,
$u \in S_\varepsilon^+$,
 \begin{align*}t_u^p \|u\|_{V_\varepsilon,p}^p + t_u^q \|u\|_{V_\varepsilon,q}^q \leqslant \sigma t_u^{2 p} \|u\|_{V_\varepsilon,p}^{2 p} + C_\sigma t_u^{2 \nu} \|u\|_{V_\varepsilon,q}^{2 \nu}.\end{align*}
\begin{align*}t_u^p \|u\|_{V_\varepsilon,p}^p + t_u^q \|u\|_{V_\varepsilon,q}^q \leqslant \sigma t_u^{2 p} \|u\|_{V_\varepsilon,p}^{2 p} + C_\sigma t_u^{2 \nu} \|u\|_{V_\varepsilon,q}^{2 \nu}.\end{align*} Assume that ![]() $t_u \leqslant 1$. Choosing
$t_u \leqslant 1$. Choosing  $\sigma = \frac{1}{2}$, we have
$\sigma = \frac{1}{2}$, we have
 \begin{align*}
Ct_u^q & \leqslant \frac{1}{2} t_u^q \left(\|u\|_{V_\varepsilon,p}^q + \|u\|_{V_\varepsilon,q}^q\right) \ \text{for some constant } C \gt 0\\
& \leqslant \frac{1}{2} t_u^p \|u\|_{V_\varepsilon,p}^p + t_u^q \|u\|_{V_\varepsilon,q}^q\ (\text{since } q \gt p,\, t_u \leqslant 1 \ \text{and } 1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,p})\\
& \leqslant C_{1 / 2} t_u^{2 \nu}\ (\text{since } 1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,q}),\\
\Rightarrow\ \ & t_u \geqslant \tau \ \text{for some constant } \tau \gt 0\ (\text{since } \nu \gt q), \ \text{where } \tau \ \text{is independent of } u.
\end{align*}
\begin{align*}
Ct_u^q & \leqslant \frac{1}{2} t_u^q \left(\|u\|_{V_\varepsilon,p}^q + \|u\|_{V_\varepsilon,q}^q\right) \ \text{for some constant } C \gt 0\\
& \leqslant \frac{1}{2} t_u^p \|u\|_{V_\varepsilon,p}^p + t_u^q \|u\|_{V_\varepsilon,q}^q\ (\text{since } q \gt p,\, t_u \leqslant 1 \ \text{and } 1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,p})\\
& \leqslant C_{1 / 2} t_u^{2 \nu}\ (\text{since } 1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,q}),\\
\Rightarrow\ \ & t_u \geqslant \tau \ \text{for some constant } \tau \gt 0\ (\text{since } \nu \gt q), \ \text{where } \tau \ \text{is independent of } u.
\end{align*} Assume that ![]() $t_u \gt 1$. Taking σ = 1 and applying
$t_u \gt 1$. Taking σ = 1 and applying ![]() $1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,p}$, we get
$1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,p}$, we get
 \begin{align*}
C t_u^p & \leqslant t_u^p \left(\|u\|_{V_\varepsilon, p}^q + \|u\|_{V_\varepsilon, q}^q\right) \ \text{for some constant } C \gt 0\\
& \leqslant t_u^p \|u\|_{V_\varepsilon,p}^p + t_u^q \|u\|_{V_\varepsilon,q}^q \ (\text{since } q \gt p \ \text{and } 1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,p})\\
& \leqslant (1 + C_1) t_u^{2 \nu}\ (\text{since } q \gt p,\, t_u \gt 1 \ \text{and } 1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,p},\ \|u\|_{V_\varepsilon,q}),\\
\Rightarrow\ \ & t_u \geqslant \tau \ \text{for some constant } \tau \gt 0 \ (\text{since } \nu \gt q), \ \text{where } \tau \ \text{is independent of } u.
\end{align*}
\begin{align*}
C t_u^p & \leqslant t_u^p \left(\|u\|_{V_\varepsilon, p}^q + \|u\|_{V_\varepsilon, q}^q\right) \ \text{for some constant } C \gt 0\\
& \leqslant t_u^p \|u\|_{V_\varepsilon,p}^p + t_u^q \|u\|_{V_\varepsilon,q}^q \ (\text{since } q \gt p \ \text{and } 1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,p})\\
& \leqslant (1 + C_1) t_u^{2 \nu}\ (\text{since } q \gt p,\, t_u \gt 1 \ \text{and } 1 = \|u\|_{X_\varepsilon} \geqslant \|u\|_{V_\varepsilon,p},\ \|u\|_{V_\varepsilon,q}),\\
\Rightarrow\ \ & t_u \geqslant \tau \ \text{for some constant } \tau \gt 0 \ (\text{since } \nu \gt q), \ \text{where } \tau \ \text{is independent of } u.
\end{align*} So, there exists τ > 0 independent of u such that ![]() $t_u \geqslant \tau$ for all
$t_u \geqslant \tau$ for all ![]() $u \in S_\varepsilon^+.$
$u \in S_\varepsilon^+.$
Let ![]() $\mathcal{W} \subset S_\varepsilon^+$ be a compact set. Arguing by contradiction, we may assume that there exists a sequence
$\mathcal{W} \subset S_\varepsilon^+$ be a compact set. Arguing by contradiction, we may assume that there exists a sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset \mathcal{W}$ such that
$\{u_n\}_{n \in \mathbb{N}} \subset \mathcal{W}$ such that ![]() $1 \leqslant t_n :=t_{u_n} \rightarrow + \infty$ as
$1 \leqslant t_n :=t_{u_n} \rightarrow + \infty$ as ![]() $n \rightarrow \infty$. Since
$n \rightarrow \infty$. Since ![]() $\mathcal{W}$ is a compact set, there is
$\mathcal{W}$ is a compact set, there is ![]() $u \in \mathcal{W}$ such that
$u \in \mathcal{W}$ such that ![]() $u_n \rightarrow u$ in Xɛ as
$u_n \rightarrow u$ in Xɛ as ![]() $n \rightarrow \infty$. As in the proof of lemma 2.2-(a), together with Fatou’s Lemma, we can see that
$n \rightarrow \infty$. As in the proof of lemma 2.2-(a), together with Fatou’s Lemma, we can see that
In addition, for any fixed ![]() $\varphi \in \mathcal{N}_\varepsilon$, we have
$\varphi \in \mathcal{N}_\varepsilon$, we have ![]() $\langle J_\varepsilon'(\varphi), \varphi \rangle = 0$. Combining
$\langle J_\varepsilon'(\varphi), \varphi \rangle = 0$. Combining ![]() $(g_3)_i$ with
$(g_3)_i$ with ![]() $(g_3)_{ii}$, we have
$(g_3)_{ii}$, we have
 \begin{align*}
J_\varepsilon(\varphi) & = J_\varepsilon(\varphi) - \frac{1}{2 p} \langle J_\varepsilon'(\varphi), \varphi \rangle \\
& \geqslant \left(\frac{1}{q} - \frac{1}{2p}\right) \left(\|\varphi\|_{V_\varepsilon,p}^p + \|\varphi\|_{V_\varepsilon,q}^q\right).
\end{align*}
\begin{align*}
J_\varepsilon(\varphi) & = J_\varepsilon(\varphi) - \frac{1}{2 p} \langle J_\varepsilon'(\varphi), \varphi \rangle \\
& \geqslant \left(\frac{1}{q} - \frac{1}{2p}\right) \left(\|\varphi\|_{V_\varepsilon,p}^p + \|\varphi\|_{V_\varepsilon,q}^q\right).
\end{align*} Taking ![]() $\varphi_n = t_n u_n \in \mathcal{N}_\varepsilon$ in the above inequality, we get
$\varphi_n = t_n u_n \in \mathcal{N}_\varepsilon$ in the above inequality, we get
 \begin{align*}
J_\varepsilon(t_n u_n) & \geqslant \left(\frac{1}{q} - \frac{1}{2p}\right) \left(t_n^p \|u_n\|_{V_\varepsilon,p}^p + t_n^q \|u_n\|_{V_\varepsilon,q}^q\right)\\
& \geqslant \left(\frac{1}{q} - \frac{1}{2p}\right) \left(t_n^p \|u_n\|_{V_\varepsilon,p}^q + t_n^q \|u_n\|_{V_\varepsilon,q}^q\right)\\
& (\text{since } q \gt p,\ t_n \geqslant 1 \ \text{and } 1 = \|u_n\|_{X_\varepsilon} \geqslant \|u_n\|_{V_\varepsilon,p})\\
& \geqslant C t_n^p \ \text{for some constant } C \gt 0,\\
\Rightarrow\ \ & - \infty \geqslant + \infty \ (\text{see (2.4) and use the assumption } t_n \rightarrow + \infty \ \text{as } n \rightarrow \infty).
\end{align*}
\begin{align*}
J_\varepsilon(t_n u_n) & \geqslant \left(\frac{1}{q} - \frac{1}{2p}\right) \left(t_n^p \|u_n\|_{V_\varepsilon,p}^p + t_n^q \|u_n\|_{V_\varepsilon,q}^q\right)\\
& \geqslant \left(\frac{1}{q} - \frac{1}{2p}\right) \left(t_n^p \|u_n\|_{V_\varepsilon,p}^q + t_n^q \|u_n\|_{V_\varepsilon,q}^q\right)\\
& (\text{since } q \gt p,\ t_n \geqslant 1 \ \text{and } 1 = \|u_n\|_{X_\varepsilon} \geqslant \|u_n\|_{V_\varepsilon,p})\\
& \geqslant C t_n^p \ \text{for some constant } C \gt 0,\\
\Rightarrow\ \ & - \infty \geqslant + \infty \ (\text{see (2.4) and use the assumption } t_n \rightarrow + \infty \ \text{as } n \rightarrow \infty).
\end{align*}This is a contradiction.
(c) As in lemma 2.2-(a), we can define the maps ![]() $\hat{m}_\varepsilon : {X_\varepsilon^+} \mapsto \mathcal{N}_\varepsilon$ and
$\hat{m}_\varepsilon : {X_\varepsilon^+} \mapsto \mathcal{N}_\varepsilon$ and ![]() $m_\varepsilon : S_\varepsilon^+ \mapsto \mathcal{N}_\varepsilon $ by
$m_\varepsilon : S_\varepsilon^+ \mapsto \mathcal{N}_\varepsilon $ by
 \begin{align}
\hat{m}_\varepsilon(u) = t_u u \quad \ \text{and } \quad m_\varepsilon = \hat{m}_\varepsilon |_{S_\varepsilon^+}.
\end{align}
\begin{align}
\hat{m}_\varepsilon(u) = t_u u \quad \ \text{and } \quad m_\varepsilon = \hat{m}_\varepsilon |_{S_\varepsilon^+}.
\end{align} Firstly, we note that ![]() $\hat{m}_\varepsilon$, mɛ, and
$\hat{m}_\varepsilon$, mɛ, and ![]() $m_\varepsilon^{- 1}$ are well-defined. Indeed, using lemma 2.2 (a), for any fixed
$m_\varepsilon^{- 1}$ are well-defined. Indeed, using lemma 2.2 (a), for any fixed ![]() $u \in {X_\varepsilon^+}$ it follows that there exists a unique
$u \in {X_\varepsilon^+}$ it follows that there exists a unique ![]() $\hat{m}_\varepsilon(u) \in \mathcal{N}_\varepsilon$. In addition, if
$\hat{m}_\varepsilon(u) \in \mathcal{N}_\varepsilon$. In addition, if ![]() $u \in \mathcal{N}_\varepsilon$, and so
$u \in \mathcal{N}_\varepsilon$, and so ![]() $u \in {X_\varepsilon^+}$. Otherwise, we obtain
$u \in {X_\varepsilon^+}$. Otherwise, we obtain ![]() $|{\mathrm{supp}\,}(u^+)| = 0$. The above equality, hypothesis
$|{\mathrm{supp}\,}(u^+)| = 0$. The above equality, hypothesis ![]() $(V_1)$, the definition of g yield that u = 0. This is impossible since u ≠ 0. Thus, the inverse of mɛ is given by
$(V_1)$, the definition of g yield that u = 0. This is impossible since u ≠ 0. Thus, the inverse of mɛ is given by  $m_\varepsilon^{- 1}(u) = \frac{u}{\|u\|_{X_\varepsilon}} \in S_\varepsilon^+$ for all
$m_\varepsilon^{- 1}(u) = \frac{u}{\|u\|_{X_\varepsilon}} \in S_\varepsilon^+$ for all ![]() $u \in \mathcal{N}_\varepsilon$. Consequently,
$u \in \mathcal{N}_\varepsilon$. Consequently, ![]() $m_\varepsilon^{- 1}$ is well-defined and continuous. On the other hand, for all
$m_\varepsilon^{- 1}$ is well-defined and continuous. On the other hand, for all ![]() $u \in S_\varepsilon^+$, we can deduce that
$u \in S_\varepsilon^+$, we can deduce that
 \begin{align*}m_\varepsilon^{- 1}(m_\varepsilon(u)) = m_\varepsilon^{- 1}(t_u u) = \frac{t_u u}{\|t_u u\|_{X_\varepsilon}} = \frac{u}{\|u\|_{X_\varepsilon}} = u.\end{align*}
\begin{align*}m_\varepsilon^{- 1}(m_\varepsilon(u)) = m_\varepsilon^{- 1}(t_u u) = \frac{t_u u}{\|t_u u\|_{X_\varepsilon}} = \frac{u}{\|u\|_{X_\varepsilon}} = u.\end{align*}This yields that mɛ is bijection.
Next, we show that ![]() $\hat{m}_\varepsilon$ is a continuous map. To this end, let
$\hat{m}_\varepsilon$ is a continuous map. To this end, let ![]() $\{u_n,u\}_{n \in \mathbb{N}} \subset {X_\varepsilon^+}$ such that
$\{u_n,u\}_{n \in \mathbb{N}} \subset {X_\varepsilon^+}$ such that ![]() $u_n \rightarrow u$ in Xɛ as
$u_n \rightarrow u$ in Xɛ as ![]() $n \rightarrow \infty$. On account of the fact that
$n \rightarrow \infty$. On account of the fact that ![]() $\hat{m}_\varepsilon (t u) = \hat{m}_\varepsilon(u)$ for all t > 0, we can assume that
$\hat{m}_\varepsilon (t u) = \hat{m}_\varepsilon(u)$ for all t > 0, we can assume that ![]() $\|u_n\|_{X_\varepsilon} = \|u\|_{X_\varepsilon} = 1$ for all
$\|u_n\|_{X_\varepsilon} = \|u\|_{X_\varepsilon} = 1$ for all ![]() $n \in \mathbb{N}$. According to lemma 2.2 (b), we know that there exists
$n \in \mathbb{N}$. According to lemma 2.2 (b), we know that there exists ![]() $t_n :=t_{u_n} \rightarrow t_0 \gt 0$ as
$t_n :=t_{u_n} \rightarrow t_0 \gt 0$ as ![]() $n \rightarrow \infty$ such that
$n \rightarrow \infty$ such that ![]() $t_n u_n \in \mathcal{N}_\varepsilon$, then we have
$t_n u_n \in \mathcal{N}_\varepsilon$, then we have
 \begin{align*}t_n^p \|u_n\|_{V_\varepsilon,p}^p + t_n^q \|u_n\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, t_n u_n)\right) g(\varepsilon x, t_nu_n) t_n u_n dx.\end{align*}
\begin{align*}t_n^p \|u_n\|_{V_\varepsilon,p}^p + t_n^q \|u_n\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, t_n u_n)\right) g(\varepsilon x, t_nu_n) t_n u_n dx.\end{align*} In the above relation, we pass to the limit as ![]() $n \rightarrow \infty$. Then,
$n \rightarrow \infty$. Then,
 \begin{align*}t_0^p \|u\|_{V_\varepsilon,p}^p + t_0^q \|u\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, t_0 u)\right) g(\varepsilon x, t_0u) t_0 u dx.\end{align*}
\begin{align*}t_0^p \|u\|_{V_\varepsilon,p}^p + t_0^q \|u\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, t_0 u)\right) g(\varepsilon x, t_0u) t_0 u dx.\end{align*} This implies that ![]() $t_0 u \in \mathcal{N}_\varepsilon$. From lemma 2.2 (a), we know that
$t_0 u \in \mathcal{N}_\varepsilon$. From lemma 2.2 (a), we know that ![]() $t_u = t_0$. Hence, it follows that
$t_u = t_0$. Hence, it follows that ![]() $\hat{m}_\varepsilon(u_n) \rightarrow \hat{m}_\varepsilon(u)$ in
$\hat{m}_\varepsilon(u_n) \rightarrow \hat{m}_\varepsilon(u)$ in ![]() ${X_\varepsilon^+}$ as
${X_\varepsilon^+}$ as ![]() $n \rightarrow \infty$. Thus,
$n \rightarrow \infty$. Thus, ![]() $\hat{m}_\varepsilon$ and mɛ are continuous mappings.
$\hat{m}_\varepsilon$ and mɛ are continuous mappings.
(d) For ɛ > 0, ![]() $0 \lt t \lt 1$, and
$0 \lt t \lt 1$, and ![]() $u \in S_\varepsilon^+$, using theorem 4.3 of Lieb and Loss [Reference Lieb and Loss38],
$u \in S_\varepsilon^+$, using theorem 4.3 of Lieb and Loss [Reference Lieb and Loss38], ![]() $(g_2)$,
$(g_2)$, ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, (2.1), and hypothesis
$(f_2)$, (2.1), and hypothesis ![]() $(V_1)$ again, we can conclude that there exists C > 0 such that
$(V_1)$ again, we can conclude that there exists C > 0 such that
 \begin{align*}J_\varepsilon(t u) \geqslant \frac{1}{2^{q - 1}q} t^{q} - C t^{2 p}.\end{align*}
\begin{align*}J_\varepsilon(t u) \geqslant \frac{1}{2^{q - 1}q} t^{q} - C t^{2 p}.\end{align*} Thus, we can find ![]() $\varrho_0 \gt 0$ such that
$\varrho_0 \gt 0$ such that ![]() $J_\varepsilon(t u) \geqslant \varrho_0$ for
$J_\varepsilon(t u) \geqslant \varrho_0$ for ![]() $0 \lt t \lt 1$ sufficiently small (since
$0 \lt t \lt 1$ sufficiently small (since ![]() $2 p \gt q \gt 0$), where ϱ 0 is independent of
$2 p \gt q \gt 0$), where ϱ 0 is independent of ![]() $\varepsilon,$ K, and a. In addition, by lemma 2.2 (a), (b), and (c), we observe (see the study by Szulkin and Weth [Reference Szulkin, Weth, Gao and Motreanu55]) that
$\varepsilon,$ K, and a. In addition, by lemma 2.2 (a), (b), and (c), we observe (see the study by Szulkin and Weth [Reference Szulkin, Weth, Gao and Motreanu55]) that
 \begin{align*}c_\varepsilon = \inf_{u \in \mathcal{N}_\varepsilon} J_\varepsilon(u) = \inf_{u \in {X_\varepsilon^+}} \max_{t \gt 0} J_\varepsilon(t u) = \inf_{u \in S_\varepsilon^+} \max_{t \gt 0} J_\varepsilon(t u).\end{align*}
\begin{align*}c_\varepsilon = \inf_{u \in \mathcal{N}_\varepsilon} J_\varepsilon(u) = \inf_{u \in {X_\varepsilon^+}} \max_{t \gt 0} J_\varepsilon(t u) = \inf_{u \in S_\varepsilon^+} \max_{t \gt 0} J_\varepsilon(t u).\end{align*} So, ![]() $J_\varepsilon(u) |_{\mathcal{N}_\varepsilon} \geqslant\varrho_0$.
$J_\varepsilon(u) |_{\mathcal{N}_\varepsilon} \geqslant\varrho_0$.
(e) Let ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset S_\varepsilon^+$ be a sequence such that
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset S_\varepsilon^+$ be a sequence such that ![]() ${\mathrm{dist}\,}(u_n,\partial S_\varepsilon^+) \rightarrow 0$ as
${\mathrm{dist}\,}(u_n,\partial S_\varepsilon^+) \rightarrow 0$ as ![]() $n \rightarrow \infty$. For any
$n \rightarrow \infty$. For any ![]() $\varphi \in \partial S_\varepsilon^+$ and
$\varphi \in \partial S_\varepsilon^+$ and ![]() $n \in \mathbb{N}$, then we obtain
$n \in \mathbb{N}$, then we obtain ![]() $|u_n^+| \leqslant |u_n - \varphi|$ a.e. in
$|u_n^+| \leqslant |u_n - \varphi|$ a.e. in ![]() $\Lambda_\varepsilon$. Hence, from
$\Lambda_\varepsilon$. Hence, from ![]() $(V_1)$ and Sobolev embedding, for any
$(V_1)$ and Sobolev embedding, for any ![]() $r \in [p,q_s^*]$ and
$r \in [p,q_s^*]$ and ![]() $n \in \mathbb{N}$, it follows that
$n \in \mathbb{N}$, it follows that
 \begin{align*}
|u_n^+|_{L^r(\Lambda_\varepsilon)} & \leqslant \inf_{\varphi \in \partial S_\varepsilon^+} |u_n - \varphi|_{L^r(\Lambda_\varepsilon)} \leqslant C_r \inf_{\varphi \in \partial S_\varepsilon^+} \|u_n - \varphi\|_{X_\varepsilon}.
\end{align*}
\begin{align*}
|u_n^+|_{L^r(\Lambda_\varepsilon)} & \leqslant \inf_{\varphi \in \partial S_\varepsilon^+} |u_n - \varphi|_{L^r(\Lambda_\varepsilon)} \leqslant C_r \inf_{\varphi \in \partial S_\varepsilon^+} \|u_n - \varphi\|_{X_\varepsilon}.
\end{align*} Taking into account ![]() $\|u_n\|_{X_\varepsilon} = 1$ and using hypothesis
$\|u_n\|_{X_\varepsilon} = 1$ and using hypothesis ![]() $(V_1)$, we have
$(V_1)$, we have
 \begin{align*}
\|u_n\|_{W^{s,p}(\mathbb{R}^N)}^p + \|u_n\|_{W^{s,q}(\mathbb{R}^N)}^q & \leqslant \frac{1}{\min\left\{V_0,1\right\}}\left(\|u_n\|_{V_\varepsilon,p}^p + \|u_n\|_{V_\varepsilon,q}^q\right) \\
&\leqslant \frac{1}{\min\left\{V_0,1\right\}}\left(\|u_n\|_{X_\varepsilon}^p + \|u_n\|_{X_\varepsilon}^q\right) \\
&\leqslant \frac{2}{V_0} + 2.
\end{align*}
\begin{align*}
\|u_n\|_{W^{s,p}(\mathbb{R}^N)}^p + \|u_n\|_{W^{s,q}(\mathbb{R}^N)}^q & \leqslant \frac{1}{\min\left\{V_0,1\right\}}\left(\|u_n\|_{V_\varepsilon,p}^p + \|u_n\|_{V_\varepsilon,q}^q\right) \\
&\leqslant \frac{1}{\min\left\{V_0,1\right\}}\left(\|u_n\|_{X_\varepsilon}^p + \|u_n\|_{X_\varepsilon}^q\right) \\
&\leqslant \frac{2}{V_0} + 2.
\end{align*} Note that ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq).$ Then, for all t > 0, we can deduce from lemma 2.6,
$\nu \lt (N - \mu) q / (N - sq).$ Then, for all t > 0, we can deduce from lemma 2.6, ![]() $(V_1)$,
$(V_1)$, ![]() $(g_3)_{ii}$,
$(g_3)_{ii}$, ![]() $(g_2)$, and
$(g_2)$, and ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$ that
$(f_2)$ that
 \begin{align*}
& \quad \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, tu_n) \right) G(\varepsilon x, tu_n) dx \\
& = \frac{K}{2}\int_{\Lambda_\varepsilon^c} G(\varepsilon x, tu_n) dx + \frac{K}{2} \int_{\Lambda_\varepsilon} G(\varepsilon x, tu_n) dx\\
& \leqslant \frac{V_0}{2p} \int_{\Lambda_\varepsilon^c} \left(t^p|u_n|^p + t^q|u_n|^q \right) dx+ \frac{K}{2} \int_{\Lambda_\varepsilon} F(t u_n^+) dx\\
& \leqslant \frac{t^p}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^p dx+ \frac{t^q}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx + C_1 t^p \int_{\Lambda_\varepsilon} (u_n^+)^p dx\nonumber\\
& + C_2 t^\nu \int_{\Lambda_\varepsilon} (u_n^+)^\nu dx\\
& \leqslant \frac{t^p}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^p dx+ \frac{t^q}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx + \hat{C}_p t^{p} {\mathrm{dist}\,}(u_n, \partial S_\varepsilon^+)^{p} \nonumber\\
& + \hat{C}_\nu t^\nu {\mathrm{dist}\,}(u_n, \partial S_\varepsilon^+)^\nu,
\end{align*}
\begin{align*}
& \quad \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, tu_n) \right) G(\varepsilon x, tu_n) dx \\
& = \frac{K}{2}\int_{\Lambda_\varepsilon^c} G(\varepsilon x, tu_n) dx + \frac{K}{2} \int_{\Lambda_\varepsilon} G(\varepsilon x, tu_n) dx\\
& \leqslant \frac{V_0}{2p} \int_{\Lambda_\varepsilon^c} \left(t^p|u_n|^p + t^q|u_n|^q \right) dx+ \frac{K}{2} \int_{\Lambda_\varepsilon} F(t u_n^+) dx\\
& \leqslant \frac{t^p}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^p dx+ \frac{t^q}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx + C_1 t^p \int_{\Lambda_\varepsilon} (u_n^+)^p dx\nonumber\\
& + C_2 t^\nu \int_{\Lambda_\varepsilon} (u_n^+)^\nu dx\\
& \leqslant \frac{t^p}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^p dx+ \frac{t^q}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx + \hat{C}_p t^{p} {\mathrm{dist}\,}(u_n, \partial S_\varepsilon^+)^{p} \nonumber\\
& + \hat{C}_\nu t^\nu {\mathrm{dist}\,}(u_n, \partial S_\varepsilon^+)^\nu,
\end{align*} where C 1, C 2, ![]() $\hat{C}_p$, and
$\hat{C}_p$, and ![]() $\hat{C}_\nu$ are some positive constants. So, we have
$\hat{C}_\nu$ are some positive constants. So, we have
 \begin{align}
&\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, tu_n) \right) G(\varepsilon x, tu_n) dx\nonumber\\
\leqslant \ & \frac{t^p}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^p dx+ \frac{t^q}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx + o_n(1),
\end{align}
\begin{align}
&\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, tu_n) \right) G(\varepsilon x, tu_n) dx\nonumber\\
\leqslant \ & \frac{t^p}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^p dx+ \frac{t^q}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx + o_n(1),
\end{align} as ![]() $n \rightarrow \infty$. Moreover, for any t > 1, we infer that
$n \rightarrow \infty$. Moreover, for any t > 1, we infer that
 \begin{align}
& \quad \frac{t^p}{p} \|u_n\|_{V_\varepsilon,p}^p + \frac{t^q}{q} \|u_n\|_{V_\varepsilon,q}^q - \frac{t^p}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^p dx- \frac{t^q}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx\nonumber\\
& = \frac{t^p}{p} [u_n]_{s,p}^p + \frac{1}{2p} t^p \int_{\mathbb{R}^N} V(\varepsilon x) |u_n|^p dx + \frac{t^q}{q} [u_n]_{s,q}^q + \left(\frac{1}{q} - \frac{1}{2p}\right) t^q \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx\nonumber\\
& \geqslant \frac{1}{2p} t^p \|u_n\|_{V_\varepsilon,p}^p + \left(\frac{1}{q} - \frac{1}{2p}\right) t^q \|u_n\|_{V_\varepsilon,q}^q\ \left(\text{since } 2p \gt q \right)\nonumber\\
& \geqslant \frac{1}{2p} t^p \|u_n\|_{V_\varepsilon,p}^q + \left(\frac{1}{q} - \frac{1}{2p}\right) t^q \|u_n\|_{V_\varepsilon,q}^q\ (\text{due to } q \gt p \ \text{and } 1 = \|u_n\|_{X_\varepsilon} \geqslant \|u_n\|_{V_\varepsilon,p}) \nonumber\\
& \geqslant \frac{1}{2^{q - 1}} \left(\frac{1}{q} - \frac{1}{2p}\right) t^p\ (\text{since } 2p \gt q \gt p \gt 1,\ t \gt 1).
\end{align}
\begin{align}
& \quad \frac{t^p}{p} \|u_n\|_{V_\varepsilon,p}^p + \frac{t^q}{q} \|u_n\|_{V_\varepsilon,q}^q - \frac{t^p}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^p dx- \frac{t^q}{2p} \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx\nonumber\\
& = \frac{t^p}{p} [u_n]_{s,p}^p + \frac{1}{2p} t^p \int_{\mathbb{R}^N} V(\varepsilon x) |u_n|^p dx + \frac{t^q}{q} [u_n]_{s,q}^q + \left(\frac{1}{q} - \frac{1}{2p}\right) t^q \int_{\mathbb{R}^N} V(\varepsilon x)|u_n|^q dx\nonumber\\
& \geqslant \frac{1}{2p} t^p \|u_n\|_{V_\varepsilon,p}^p + \left(\frac{1}{q} - \frac{1}{2p}\right) t^q \|u_n\|_{V_\varepsilon,q}^q\ \left(\text{since } 2p \gt q \right)\nonumber\\
& \geqslant \frac{1}{2p} t^p \|u_n\|_{V_\varepsilon,p}^q + \left(\frac{1}{q} - \frac{1}{2p}\right) t^q \|u_n\|_{V_\varepsilon,q}^q\ (\text{due to } q \gt p \ \text{and } 1 = \|u_n\|_{X_\varepsilon} \geqslant \|u_n\|_{V_\varepsilon,p}) \nonumber\\
& \geqslant \frac{1}{2^{q - 1}} \left(\frac{1}{q} - \frac{1}{2p}\right) t^p\ (\text{since } 2p \gt q \gt p \gt 1,\ t \gt 1).
\end{align}Recalling that the definition of mɛ and invoking relations (2.6) and (2.7), for all t > 1, we can deduce that
 \begin{align*}\liminf_{n \rightarrow \infty} J_\varepsilon(m_\varepsilon(u_n)) \geqslant \liminf_{n \rightarrow \infty} J_\varepsilon(t u_n) \geqslant \frac{1}{2^{q - 1}} \left(\frac{1}{q} - \frac{1}{2p}\right) t^p.\end{align*}
\begin{align*}\liminf_{n \rightarrow \infty} J_\varepsilon(m_\varepsilon(u_n)) \geqslant \liminf_{n \rightarrow \infty} J_\varepsilon(t u_n) \geqslant \frac{1}{2^{q - 1}} \left(\frac{1}{q} - \frac{1}{2p}\right) t^p.\end{align*}The above inequality combined with the definition of Jɛ and the arbitrariness of t > 1 means that
 \begin{align*}
\liminf_{n \rightarrow \infty} \left(\frac{1}{p}\|m_\varepsilon(u_n)\|_{V_\varepsilon,p}^p + \frac{1}{q} \|m_\varepsilon(u_n)\|_{V_\varepsilon,q}^q\right) \geqslant \liminf_{n \rightarrow \infty} J_\varepsilon(m_\varepsilon(u_n)) = + \infty,
\end{align*}
\begin{align*}
\liminf_{n \rightarrow \infty} \left(\frac{1}{p}\|m_\varepsilon(u_n)\|_{V_\varepsilon,p}^p + \frac{1}{q} \|m_\varepsilon(u_n)\|_{V_\varepsilon,q}^q\right) \geqslant \liminf_{n \rightarrow \infty} J_\varepsilon(m_\varepsilon(u_n)) = + \infty,
\end{align*} and so ![]() $\|m_\varepsilon(u_n)\|_{X_\varepsilon} \rightarrow + \infty$ as
$\|m_\varepsilon(u_n)\|_{X_\varepsilon} \rightarrow + \infty$ as ![]() $n \rightarrow \infty$. This proof is now complete.
$n \rightarrow \infty$. This proof is now complete.
Now, we introduce the functionals
 \begin{align*}\hat{\psi}_\varepsilon : {X_\varepsilon^+} \mapsto \mathbb{R} \quad \ \text{and } \quad \psi_\varepsilon : S_\varepsilon^+ \mapsto \mathbb{R}\end{align*}
\begin{align*}\hat{\psi}_\varepsilon : {X_\varepsilon^+} \mapsto \mathbb{R} \quad \ \text{and } \quad \psi_\varepsilon : S_\varepsilon^+ \mapsto \mathbb{R}\end{align*} defined by  $\hat{\psi}_\varepsilon(u) := J_\varepsilon(\hat{m}_\varepsilon(u))$ for any
$\hat{\psi}_\varepsilon(u) := J_\varepsilon(\hat{m}_\varepsilon(u))$ for any ![]() $u \in {X_\varepsilon^+}$ and
$u \in {X_\varepsilon^+}$ and  $\psi_\varepsilon := \hat{\psi}_\varepsilon |_{S_\varepsilon^+}$.
$\psi_\varepsilon := \hat{\psi}_\varepsilon |_{S_\varepsilon^+}$.
Using lemma 2.2 and corollary 2.3 in the study by Szulkin and Weth [Reference Szulkin, Weth, Gao and Motreanu55], we deduce that the following result holds true.
Lemma 2.3. Assume that ![]() $(f_1)$–
$(f_1)$–![]() $(f_4)$ and
$(f_4)$ and ![]() $(V_1)$–
$(V_1)$–![]() $(V_2)$ are satisfied. Then,
$(V_2)$ are satisfied. Then,
(a)
 $\hat{\psi}_\varepsilon \in C^1({X_\varepsilon^+},\mathbb{R})$ and
$\hat{\psi}_\varepsilon \in C^1({X_\varepsilon^+},\mathbb{R})$ and  $\langle \hat{\psi}'_\varepsilon(u), v\rangle = \frac{\|\hat{m}_\varepsilon(u)\|_{X_\varepsilon}}{\|u\|_{X_\varepsilon}} \langle J_\varepsilon'(\hat{m}_\varepsilon(u)),v\rangle$ for all
$\langle \hat{\psi}'_\varepsilon(u), v\rangle = \frac{\|\hat{m}_\varepsilon(u)\|_{X_\varepsilon}}{\|u\|_{X_\varepsilon}} \langle J_\varepsilon'(\hat{m}_\varepsilon(u)),v\rangle$ for all  $u \in X_\varepsilon^+,$ all
$u \in X_\varepsilon^+,$ all  $v \in {X_\varepsilon};$
$v \in {X_\varepsilon};$(b)
 $\psi_\varepsilon \in C^1(S_\varepsilon^+,\mathbb{R})$ and
$\psi_\varepsilon \in C^1(S_\varepsilon^+,\mathbb{R})$ and  $\langle \psi'_\varepsilon(u),v\rangle = \|m_\varepsilon(u)\|_{X_\varepsilon} \langle J_\varepsilon'(m_\varepsilon(u)),v\rangle$ for all
$\langle \psi'_\varepsilon(u),v\rangle = \|m_\varepsilon(u)\|_{X_\varepsilon} \langle J_\varepsilon'(m_\varepsilon(u)),v\rangle$ for all  $u \in S_\varepsilon^+,$ all
$u \in S_\varepsilon^+,$ all  $v \in T_u(S_\varepsilon^+);$
$v \in T_u(S_\varepsilon^+);$(c) if
 $\{u_n\}_{n \in \mathbb{N}}$ is a Palais–Smale sequence for the functional
$\{u_n\}_{n \in \mathbb{N}}$ is a Palais–Smale sequence for the functional  $\psi_\varepsilon,$ then
$\psi_\varepsilon,$ then  $\{m_\varepsilon(u_n)\}_{n \in \mathbb{N}}$ is a Palais–Smale sequence for the functional
$\{m_\varepsilon(u_n)\}_{n \in \mathbb{N}}$ is a Palais–Smale sequence for the functional  $J_\varepsilon.$ If
$J_\varepsilon.$ If  $\{u_n\}_{n \in \mathbb{N}} \subset \mathcal{N}_\varepsilon$ is bounded Palais–Smale sequence for the functional
$\{u_n\}_{n \in \mathbb{N}} \subset \mathcal{N}_\varepsilon$ is bounded Palais–Smale sequence for the functional  $J_\varepsilon,$ then,
$J_\varepsilon,$ then,  $\{m_\varepsilon^{- 1}(u_n)\}_{n \in \mathbb{N}} \subset S_\varepsilon^+$ is a Palais–Smale sequence for
$\{m_\varepsilon^{- 1}(u_n)\}_{n \in \mathbb{N}} \subset S_\varepsilon^+$ is a Palais–Smale sequence for  $\psi_\varepsilon;$
$\psi_\varepsilon;$(d)
 $u \in S_\varepsilon^+$ is a critical point of the functional ψɛ if and only if
$u \in S_\varepsilon^+$ is a critical point of the functional ψɛ if and only if  $m_\varepsilon(u) \in \mathcal{N}_\varepsilon$ is a critical point of the functional
$m_\varepsilon(u) \in \mathcal{N}_\varepsilon$ is a critical point of the functional  $J_\varepsilon.$ Moreover, the corresponding critical values coincide and
$J_\varepsilon.$ Moreover, the corresponding critical values coincide and
 \begin{align*}\inf_{u \in S_\varepsilon^+} \psi_\varepsilon(u) = \inf_{u \in \mathcal{N}_\varepsilon}J_\varepsilon(u) = c_\varepsilon.\end{align*}
\begin{align*}\inf_{u \in S_\varepsilon^+} \psi_\varepsilon(u) = \inf_{u \in \mathcal{N}_\varepsilon}J_\varepsilon(u) = c_\varepsilon.\end{align*}
Lemma 2.4. The modified functional Jɛ admits a Palais–Smale sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ at the level
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ at the level ![]() $c_\varepsilon,$ that is,
$c_\varepsilon,$ that is, ![]() $J_\varepsilon(u_n) \rightarrow c_\varepsilon$ in
$J_\varepsilon(u_n) \rightarrow c_\varepsilon$ in ![]() $\mathbb{R}$ and
$\mathbb{R}$ and ![]() $J_\varepsilon'(u_n) \rightarrow 0$ in
$J_\varepsilon'(u_n) \rightarrow 0$ in ![]() ${X_\varepsilon}^*$ as
${X_\varepsilon}^*$ as ![]() $n \rightarrow \infty,$ where cɛ is given in lemma 2.2. Furthermore, there exists some constant ϑ > 0
$n \rightarrow \infty,$ where cɛ is given in lemma 2.2. Furthermore, there exists some constant ϑ > 0 ![]() $($independent of
$($independent of ![]() $\varepsilon,$ K, and
$\varepsilon,$ K, and ![]() $a)$ such that
$a)$ such that ![]() $c_\varepsilon \lt \vartheta$ for all ɛ sufficiently small.
$c_\varepsilon \lt \vartheta$ for all ɛ sufficiently small.
Proof. In view of lemma 2.2, we only need to verify that Jɛ possesses a mountain pass geometry, that is, the functional Jɛ satisfies the following properties:
(i) there exist some constants
 $\rho_1 \gt 0$ and
$\rho_1 \gt 0$ and  $\delta_1 \gt 0$ such that
$\delta_1 \gt 0$ such that  $J_\varepsilon(u) \geqslant \delta_1$ for
$J_\varepsilon(u) \geqslant \delta_1$ for  $\|u\|_{X_\varepsilon} = \rho_1$;
$\|u\|_{X_\varepsilon} = \rho_1$;(ii) there exists an element
 $ e \in {X_\varepsilon}$ with
$ e \in {X_\varepsilon}$ with  $\|e\|_{X_\varepsilon} \gt \rho_1$ such that
$\|e\|_{X_\varepsilon} \gt \rho_1$ such that  $J_\varepsilon(e) \lt 0$.
$J_\varepsilon(e) \lt 0$.
(i) Arguing as in the proof of lemma 2.2 (a), we find some constants C > 0 and ![]() $C' \gt 0$ such that
$C' \gt 0$ such that
 \begin{align*}J_\varepsilon(u) \geqslant C\|u\|_{X_\varepsilon}^q - C' \|u\|_{X_\varepsilon}^{2 p}\end{align*}
\begin{align*}J_\varepsilon(u) \geqslant C\|u\|_{X_\varepsilon}^q - C' \|u\|_{X_\varepsilon}^{2 p}\end{align*} for ![]() $\|u\|_{X_\varepsilon} = \rho_1 \in (0,1)$. So, using
$\|u\|_{X_\varepsilon} = \rho_1 \in (0,1)$. So, using ![]() $2 p \gt q$, we obtain (i) if we take ρ 1 small enough.
$2 p \gt q$, we obtain (i) if we take ρ 1 small enough.
(ii) We choose a suitable function ![]() $\varphi \in C_0^\infty(\mathbb{R}^N)$ such that
$\varphi \in C_0^\infty(\mathbb{R}^N)$ such that ![]() $\varphi \geqslant 0$,
$\varphi \geqslant 0$, ![]() $\varphi \not\equiv 0$, and
$\varphi \not\equiv 0$, and ![]() ${\mathrm{supp}}\, (\varphi) \subset \Lambda$. Then, for all ɛ sufficiently small, it is obvious that
${\mathrm{supp}}\, (\varphi) \subset \Lambda$. Then, for all ɛ sufficiently small, it is obvious that ![]() $G(\varepsilon x, \varphi) = F(\varphi)$ for all
$G(\varepsilon x, \varphi) = F(\varphi)$ for all ![]() $x \in \mathbb{R}^N$. Hence, with arguments as in the proof of lemma 2.2 (a), there exist two constants
$x \in \mathbb{R}^N$. Hence, with arguments as in the proof of lemma 2.2 (a), there exist two constants
 \begin{align*}C_\varphi = \frac{1}{2} \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\varphi)\right)F(\varphi) dx \gt 0\end{align*}
\begin{align*}C_\varphi = \frac{1}{2} \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\varphi)\right)F(\varphi) dx \gt 0\end{align*}and C > 0 such that
 \begin{align*}J_\varepsilon(t \varphi) \leqslant Ct^q - C_\varphi t^{2p}\end{align*}
\begin{align*}J_\varepsilon(t \varphi) \leqslant Ct^q - C_\varphi t^{2p}\end{align*} for all t > 1. Hence, (ii) holds true for ![]() $e = t \varphi$ and for some t > 1 sufficiently large.
$e = t \varphi$ and for some t > 1 sufficiently large.
According to the mountain pass theorem without the Palais–Smale condition (see the study by Brezis and Nirenberg [Reference Brezis and Nirenberg18]), we establish the existence of a Palais–Smale sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ at the level cɛ. We recall that
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ at the level cɛ. We recall that ![]() ${\mathrm{supp}}\, (\varphi) \subset \Lambda$, and then we can infer that there exists a constant ϑ > 0 such that
${\mathrm{supp}}\, (\varphi) \subset \Lambda$, and then we can infer that there exists a constant ϑ > 0 such that ![]() $c_\varepsilon \lt \vartheta$ for all ɛ small enough, where ϑ is independent of ɛ, K, and a. This completes the proof of the lemma.
$c_\varepsilon \lt \vartheta$ for all ɛ small enough, where ϑ is independent of ɛ, K, and a. This completes the proof of the lemma.
Lemma 2.5. Assume that ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is the Palais–Smale sequence of Jɛ at the level
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is the Palais–Smale sequence of Jɛ at the level ![]() $c \leqslant \vartheta,$ where ɛ > 0 small enough. Then, for ɛ > 0 small enough, the sequence
$c \leqslant \vartheta,$ where ɛ > 0 small enough. Then, for ɛ > 0 small enough, the sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is bounded and
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is bounded and
 \begin{equation*}\Arrowvert u_n\Arrowvert_{W^{s,p}(\mathbb{R}^N)}^p+\Arrowvert u_n\Arrowvert_{W^{s,q}(\mathbb{R}^N)}^q\leqslant2\left(\frac1{V_0}+1\right)\frac{pq(\vartheta+1)}{2p-q}\;\text{for all}\ n\in\mathbb{N}\;\text{large enough.}\end{equation*}
\begin{equation*}\Arrowvert u_n\Arrowvert_{W^{s,p}(\mathbb{R}^N)}^p+\Arrowvert u_n\Arrowvert_{W^{s,q}(\mathbb{R}^N)}^q\leqslant2\left(\frac1{V_0}+1\right)\frac{pq(\vartheta+1)}{2p-q}\;\text{for all}\ n\in\mathbb{N}\;\text{large enough.}\end{equation*}Proof. According to ![]() $(g_3)_{i,ii}$ and using hypothesis
$(g_3)_{i,ii}$ and using hypothesis ![]() $(V_1)$, for any ɛ > 0 small enough, we deduce that
$(V_1)$, for any ɛ > 0 small enough, we deduce that
 \begin{align}
\vartheta + o_n(1) \|u_n\|_{X_\varepsilon} & \geqslant
c + o_n(1) \|u_n\|_{X_\varepsilon}\nonumber \\
& \geqslant J_\varepsilon(u_n) - \frac{1}{2 p} \langle J_\varepsilon'(u_n),u_n\rangle\nonumber\\
& \geqslant \left(\frac{1}{q} - \frac{1}{2 p}\right) \left( \|u_n\|_{V_\varepsilon,p}^p + \|u_n\|_{V_\varepsilon,q}^q\right)\nonumber\\
& + \frac{1}{2 p}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u_n)\right) \left( g(\varepsilon x, u_n) u_n - p G(\varepsilon x, u_n) \right) dx\nonumber\\
& \geqslant \min\left\{V_0, 1\right\} \left(\frac{1}{q} - \frac{1}{2 p}\right) \left( \|u_n\|_{W^{s,p}(\mathbb{R}^N)}^p + \|u_n\|_{W^{s,q}(\mathbb{R}^N)}^q\right).
\end{align}
\begin{align}
\vartheta + o_n(1) \|u_n\|_{X_\varepsilon} & \geqslant
c + o_n(1) \|u_n\|_{X_\varepsilon}\nonumber \\
& \geqslant J_\varepsilon(u_n) - \frac{1}{2 p} \langle J_\varepsilon'(u_n),u_n\rangle\nonumber\\
& \geqslant \left(\frac{1}{q} - \frac{1}{2 p}\right) \left( \|u_n\|_{V_\varepsilon,p}^p + \|u_n\|_{V_\varepsilon,q}^q\right)\nonumber\\
& + \frac{1}{2 p}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, u_n)\right) \left( g(\varepsilon x, u_n) u_n - p G(\varepsilon x, u_n) \right) dx\nonumber\\
& \geqslant \min\left\{V_0, 1\right\} \left(\frac{1}{q} - \frac{1}{2 p}\right) \left( \|u_n\|_{W^{s,p}(\mathbb{R}^N)}^p + \|u_n\|_{W^{s,q}(\mathbb{R}^N)}^q\right).
\end{align} So, for ɛ > 0 small enough, we deduce that the sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is bounded and
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is bounded and
 \begin{equation*}\Arrowvert u_n\Arrowvert_{W^{s,p}(\mathbb{R}^N)}^p+\Arrowvert u_n\Arrowvert_{W^{s,q}(\mathbb{R}^N)}^q\leqslant2\left(\frac1{V_0}+1\right)\frac{pq(\vartheta+1)}{2p-q}\end{equation*}
\begin{equation*}\Arrowvert u_n\Arrowvert_{W^{s,p}(\mathbb{R}^N)}^p+\Arrowvert u_n\Arrowvert_{W^{s,q}(\mathbb{R}^N)}^q\leqslant2\left(\frac1{V_0}+1\right)\frac{pq(\vartheta+1)}{2p-q}\end{equation*} for all ![]() $n \in \mathbb{N}$ large enough.
$n \in \mathbb{N}$ large enough.
According to (2.8), we now define the following set:
 \begin{align*}\mathcal{B} := \left\{u \in {X_\varepsilon} : \|u\|_{W^{s,p}(\mathbb{R}^N)}^p + \|u\|_{W^{s,q}(\mathbb{R}^N)}^q \leqslant 2\left(\frac{1}{V_0} +1\right)\left(\frac{(\vartheta + 1) p q}{2 p - q} + 1 \right)\right\},\end{align*}
\begin{align*}\mathcal{B} := \left\{u \in {X_\varepsilon} : \|u\|_{W^{s,p}(\mathbb{R}^N)}^p + \|u\|_{W^{s,q}(\mathbb{R}^N)}^q \leqslant 2\left(\frac{1}{V_0} +1\right)\left(\frac{(\vartheta + 1) p q}{2 p - q} + 1 \right)\right\},\end{align*}where ϑ is given in lemma 2.4. Using the above notation, we can show the following estimate.
Lemma 2.6. Assume that ![]() $(f_1)$–
$(f_1)$–![]() $(f_4)$ hold true,
$(f_4)$ hold true, ![]() $0 \lt \mu \lt sp$, and
$0 \lt \mu \lt sp$, and ![]() $\nu \lt (N - \mu) q / (N - sq),$ then there is a constant K > 0 such that
$\nu \lt (N - \mu) q / (N - sq),$ then there is a constant K > 0 such that
 \begin{align*}\sup_{u \in \mathcal{B}} \left|\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right|_{L^\infty(\mathbb{R}^N)} \lt \frac{K}{2} \ \text{for all}\ \varepsilon \gt 0.\end{align*}
\begin{align*}\sup_{u \in \mathcal{B}} \left|\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right|_{L^\infty(\mathbb{R}^N)} \lt \frac{K}{2} \ \text{for all}\ \varepsilon \gt 0.\end{align*}Proof. Firstly, ![]() $(g_2)$ and
$(g_2)$ and ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$ imply that there exists a constant C > 0 (which is independent of ɛ) such that
$(f_2)$ imply that there exists a constant C > 0 (which is independent of ɛ) such that
Therefore,
 \begin{align*}
\left|\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right| & \leqslant \left|\frac{1}{|x|^\mu} * F(u)\right|\\
& \leqslant \int_{|x - y| \leqslant 1} \frac{|F(u(y))|}{|x - y|^\mu} dy + \int_{|x - y| \gt 1} \frac{|F(u(y))|}{|x - y|^\mu} dy\\
& \leqslant C \int_{|x -y| \leqslant 1} \frac{|u(y)|^p + |u(y)|^\nu}{|x - y|^\mu} dy \\
& \quad + C \int_{\mathbb{R}^N} \left(|u(y)|^p + |u(y)|^\nu\right) dy\ (\text{see (2.9)})\\
& \leqslant C \int_{|x -y| \leqslant 1} \frac{|u(y)|^p + |u(y)|^\nu}{|x - y|^\mu} dy \\
& \quad + C\ (\text{see (2.1) and use the definition of}\ \mathcal{B})
\end{align*}
\begin{align*}
\left|\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right| & \leqslant \left|\frac{1}{|x|^\mu} * F(u)\right|\\
& \leqslant \int_{|x - y| \leqslant 1} \frac{|F(u(y))|}{|x - y|^\mu} dy + \int_{|x - y| \gt 1} \frac{|F(u(y))|}{|x - y|^\mu} dy\\
& \leqslant C \int_{|x -y| \leqslant 1} \frac{|u(y)|^p + |u(y)|^\nu}{|x - y|^\mu} dy \\
& \quad + C \int_{\mathbb{R}^N} \left(|u(y)|^p + |u(y)|^\nu\right) dy\ (\text{see (2.9)})\\
& \leqslant C \int_{|x -y| \leqslant 1} \frac{|u(y)|^p + |u(y)|^\nu}{|x - y|^\mu} dy \\
& \quad + C\ (\text{see (2.1) and use the definition of}\ \mathcal{B})
\end{align*} for some constant C > 0 (which is independent of ![]() $x \in \mathbb{R}^N$ and ɛ > 0).
$x \in \mathbb{R}^N$ and ɛ > 0).
Let us choose
 \begin{align*}t_1 \in \left(\frac{N}{N - \mu}, \frac{N}{N - sp}\right]\quad \ \text{and} \quad t_2 \in \left(\frac{N}{N - \mu},\frac{N q}{(N - sq) \nu}\right],\end{align*}
\begin{align*}t_1 \in \left(\frac{N}{N - \mu}, \frac{N}{N - sp}\right]\quad \ \text{and} \quad t_2 \in \left(\frac{N}{N - \mu},\frac{N q}{(N - sq) \nu}\right],\end{align*} since ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq).$ Then, combining the Hölder inequality, (2.1), and the definition of
$\nu \lt (N - \mu) q / (N - sq).$ Then, combining the Hölder inequality, (2.1), and the definition of ![]() $\mathcal{B}$, we can easily see that
$\mathcal{B}$, we can easily see that
 \begin{align*}\int_{|x -y| \leqslant 1} \frac{|u(y)|^p + |u(y)|^\nu}{|x - y|^\mu} dy \leqslant C \ \text{for all}\ x \in \mathbb{R}^N.\end{align*}
\begin{align*}\int_{|x -y| \leqslant 1} \frac{|u(y)|^p + |u(y)|^\nu}{|x - y|^\mu} dy \leqslant C \ \text{for all}\ x \in \mathbb{R}^N.\end{align*} for some constant C > 0 (which is independent of ![]() $x \in \mathbb{R}^N$ and ɛ > 0). So, from the above information, we complete the proof of this lemma.
$x \in \mathbb{R}^N$ and ɛ > 0). So, from the above information, we complete the proof of this lemma.
Now, we show that the modified functional Jɛ satisfies the Palais–Smale condition.
Lemma 2.7. Let ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq).$ Then, for all ɛ > 0 sufficiently small, the modified functional Jɛ satisfies the Palais–Smale condition with
$\nu \lt (N - \mu) q / (N - sq).$ Then, for all ɛ > 0 sufficiently small, the modified functional Jɛ satisfies the Palais–Smale condition with ![]() $c \leqslant \vartheta$.
$c \leqslant \vartheta$.
Proof. For all ɛ > 0 sufficiently small, let ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ be a Palais–Smale sequence of the functional Jɛ at the level c. From lemma 2.5, we know that
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ be a Palais–Smale sequence of the functional Jɛ at the level c. From lemma 2.5, we know that ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is bounded for all ɛ > 0 small enough. So, passing to a subsequence, we may assume that there exists some
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is bounded for all ɛ > 0 small enough. So, passing to a subsequence, we may assume that there exists some ![]() $u \in {X_\varepsilon}$ such that
$u \in {X_\varepsilon}$ such that ![]() $u_n \xrightarrow w u$ in Xɛ,
$u_n \xrightarrow w u$ in Xɛ, ![]() $u_n(x) \rightarrow u(x)$ a.e. in
$u_n(x) \rightarrow u(x)$ a.e. in ![]() $\mathbb{R}^N$ and
$\mathbb{R}^N$ and ![]() $u_n \rightarrow u$ in
$u_n \rightarrow u$ in ![]() $L^r_{\mathrm{loc}}(\mathbb{R}^N)$ for all
$L^r_{\mathrm{loc}}(\mathbb{R}^N)$ for all ![]() $r \in [1,q_s^*)$ as
$r \in [1,q_s^*)$ as ![]() $n \rightarrow \infty$. We first assert that the following property is fulfilled.
$n \rightarrow \infty$. We first assert that the following property is fulfilled.
Claim 1: The following properties hold up to a subsequence:
(a)
 $\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * \left(G(\varepsilon x,u_n) -G(\varepsilon x,u)\right)\right) g(\varepsilon x,u) \varphi dx
= 0$ for all
$\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * \left(G(\varepsilon x,u_n) -G(\varepsilon x,u)\right)\right) g(\varepsilon x,u) \varphi dx
= 0$ for all  $\varphi \in C^\infty_0(\mathbb{R}^N)$;
$\varphi \in C^\infty_0(\mathbb{R}^N)$;(b)
 $\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u_n)\right) \left(g(\varepsilon x,u_n) - g(\varepsilon x,u) \right) \varphi dx = 0$ for all
$\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u_n)\right) \left(g(\varepsilon x,u_n) - g(\varepsilon x,u) \right) \varphi dx = 0$ for all  $\varphi \in C^\infty_0(\mathbb{R}^N)$;
$\varphi \in C^\infty_0(\mathbb{R}^N)$;(c) we have
 \begin{align*}
&\lim_{n \rightarrow \infty} \int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * G(\varepsilon x, u_n)\right) g(\varepsilon x,u_n) \varphi dx\\
=\ & \int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right) g(\varepsilon x,u) \varphi dx \ \text{for all}\ \varphi \in C^\infty_0(\mathbb{R}^N).
\end{align*}
\begin{align*}
&\lim_{n \rightarrow \infty} \int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * G(\varepsilon x, u_n)\right) g(\varepsilon x,u_n) \varphi dx\\
=\ & \int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * G(\varepsilon x, u)\right) g(\varepsilon x,u) \varphi dx \ \text{for all}\ \varphi \in C^\infty_0(\mathbb{R}^N).
\end{align*}
(a) Note that
 \begin{align*}
\int_{\mathbb{R}^N} |G(\varepsilon x,u_n)|^{\frac{2 N}{2 N - \mu}} dx & \leqslant \int_{\mathbb{R}^N} \left|C\left(|u_n|^p + |u_n|^{\nu} \right)\right|^{\frac{2 N}{2 N - \mu}} dx \ (\text{see (2.9)})\\
& \leqslant C \int_{\mathbb{R}^N} \left(|u_n|^{\frac{2 N p}{2 N - \mu}} + |u_n|^{\frac{2 N \nu}{2 N - \mu}}\right) dx\\
& \leqslant C \left(\|u_n\|_{X_\varepsilon}^{2 N p /(2 N - \mu)} + \|u_n\|_{X_\varepsilon}^{2 N \nu /(2 N - \mu)} \right)\ (\text{see (2.1)})\\
& \leqslant C \ (\text{due to the boundedness of the sequence}\ \{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}).
\end{align*}
\begin{align*}
\int_{\mathbb{R}^N} |G(\varepsilon x,u_n)|^{\frac{2 N}{2 N - \mu}} dx & \leqslant \int_{\mathbb{R}^N} \left|C\left(|u_n|^p + |u_n|^{\nu} \right)\right|^{\frac{2 N}{2 N - \mu}} dx \ (\text{see (2.9)})\\
& \leqslant C \int_{\mathbb{R}^N} \left(|u_n|^{\frac{2 N p}{2 N - \mu}} + |u_n|^{\frac{2 N \nu}{2 N - \mu}}\right) dx\\
& \leqslant C \left(\|u_n\|_{X_\varepsilon}^{2 N p /(2 N - \mu)} + \|u_n\|_{X_\varepsilon}^{2 N \nu /(2 N - \mu)} \right)\ (\text{see (2.1)})\\
& \leqslant C \ (\text{due to the boundedness of the sequence}\ \{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}).
\end{align*} On the other hand, since ![]() $u_n(x) \rightarrow u(x)$ a.e. in
$u_n(x) \rightarrow u(x)$ a.e. in ![]() $\mathbb{R}^N$ as
$\mathbb{R}^N$ as ![]() $n \rightarrow \infty$, we obtain
$n \rightarrow \infty$, we obtain
From proposition 5.4.7 in the study by Willem [Reference Willem58], it follows that
 \begin{align}
G(\varepsilon \cdot,u_n) \xrightarrow w G(\varepsilon \cdot, u) \ \text{in}\ L^{\frac{2 N}{2N - \mu}}(\mathbb{R}^N) \ \text{as}\ n \rightarrow \infty.
\end{align}
\begin{align}
G(\varepsilon \cdot,u_n) \xrightarrow w G(\varepsilon \cdot, u) \ \text{in}\ L^{\frac{2 N}{2N - \mu}}(\mathbb{R}^N) \ \text{as}\ n \rightarrow \infty.
\end{align}Let us define
 \begin{align*}H(w) := \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * w(x)\right) g(\varepsilon x,u) \varphi dx \ \text{for all}\ w \in L^{\frac{2 N}{2 N - \mu}}(\mathbb{R}^N).\end{align*}
\begin{align*}H(w) := \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * w(x)\right) g(\varepsilon x,u) \varphi dx \ \text{for all}\ w \in L^{\frac{2 N}{2 N - \mu}}(\mathbb{R}^N).\end{align*}Then, it follows from theorem 4.3 of [Reference Lieb and Loss38], ![]() $(g_2)$,
$(g_2)$, ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, Hölder’s inequality, (2.1), and
$(f_2)$, Hölder’s inequality, (2.1), and ![]() $u\in {X_\varepsilon}$ that H is linear bounded functional. Combining this with (2.10), we derive that (a) holds true.
$u\in {X_\varepsilon}$ that H is linear bounded functional. Combining this with (2.10), we derive that (a) holds true.
(b) Using the boundedness of the sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, together with theorem 4.3 in the study by Lieb and Loss [Reference Lieb and Loss38],
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, together with theorem 4.3 in the study by Lieb and Loss [Reference Lieb and Loss38], ![]() $(g_2)$,
$(g_2)$, ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, and (2.1), we see that
$(f_2)$, and (2.1), we see that ![]() $G(\varepsilon \cdot,u_n)$ is also bounded in
$G(\varepsilon \cdot,u_n)$ is also bounded in  $L^{\frac{2 N}{2 N -\mu}}(\mathbb{R}^N)$. Then, applying the boundedness of the sequence
$L^{\frac{2 N}{2 N -\mu}}(\mathbb{R}^N)$. Then, applying the boundedness of the sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ again and combining with the compact embeddings and Dominated Convergence Theorem, we deduce that (b) is also true.
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ again and combining with the compact embeddings and Dominated Convergence Theorem, we deduce that (b) is also true.
(c) This result is a consequence of (a) and (b).
Next, we consider the following sequence:
 \begin{align*}b_n(x,y) := \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))}{|x - y|^{\frac{N + s p}{p'}}}\end{align*}
\begin{align*}b_n(x,y) := \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))}{|x - y|^{\frac{N + s p}{p'}}}\end{align*}and we also introduce the following function
 \begin{align*}b(x,y) := \frac{|u(x) - u(y)|^{p - 2} (u(x) - u(y))}{|x - y|^{\frac{N + s p}{p'}}},\end{align*}
\begin{align*}b(x,y) := \frac{|u(x) - u(y)|^{p - 2} (u(x) - u(y))}{|x - y|^{\frac{N + s p}{p'}}},\end{align*} where  $p' = \frac{p}{p - 1}$. Then,
$p' = \frac{p}{p - 1}$. Then,  $\{b_n\}_{n \in \mathbb{N}} \subset L^{p'}(\mathbb{R}^{2 N})$ is bounded and
$\{b_n\}_{n \in \mathbb{N}} \subset L^{p'}(\mathbb{R}^{2 N})$ is bounded and ![]() $b_n(x,y) \rightarrow b(x,y)$ a.e. in
$b_n(x,y) \rightarrow b(x,y)$ a.e. in ![]() $\mathbb{R}^{2 N}$ as
$\mathbb{R}^{2 N}$ as ![]() $n \rightarrow \infty$. Then, we deduce from proposition 5.4.7 in the study by Willem [Reference Willem58] that
$n \rightarrow \infty$. Then, we deduce from proposition 5.4.7 in the study by Willem [Reference Willem58] that
 \begin{align}
b_n \xrightarrow w b \ \text{in}\ L^{p'}(\mathbb{R}^{2 N}) \ \text{as } n \rightarrow \infty.
\end{align}
\begin{align}
b_n \xrightarrow w b \ \text{in}\ L^{p'}(\mathbb{R}^{2 N}) \ \text{as } n \rightarrow \infty.
\end{align} On the other hand, for all ![]() $\varphi \in C^\infty_0(\mathbb{R}^N)$, we see that
$\varphi \in C^\infty_0(\mathbb{R}^N)$, we see that
 \begin{align*}\frac{\varphi(x) - \varphi(y)}{|x - y|^{\frac{N + s p}{p}}} \in L^p(\mathbb{R}^{2 N}).\end{align*}
\begin{align*}\frac{\varphi(x) - \varphi(y)}{|x - y|^{\frac{N + s p}{p}}} \in L^p(\mathbb{R}^{2 N}).\end{align*}From this and (2.11), we have
 \begin{align*}
&\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y)) (\varphi(x) - \varphi(y))}{|x - y|^{N + s p}} dxdy\\
=\ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u(x) - u(y)|^{p - 2} (u(x) - u(y)) (\varphi(x) - \varphi(y))}{|x - y|^{N + s p}} dxdy.
\end{align*}
\begin{align*}
&\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y)) (\varphi(x) - \varphi(y))}{|x - y|^{N + s p}} dxdy\\
=\ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u(x) - u(y)|^{p - 2} (u(x) - u(y)) (\varphi(x) - \varphi(y))}{|x - y|^{N + s p}} dxdy.
\end{align*}In a similar fashion, we also have
 \begin{align*}
&\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{q - 2} (u_n(x) - u_n(y)) (\varphi(x) - \varphi(y))}{|x - y|^{N + s q}} dxdy\\
=\ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u(x) - u(y)|^{q - 2} (u(x) - u(y)) (\varphi(x) - \varphi(y))}{|x - y|^{N + s q}} dxdy.
\end{align*}
\begin{align*}
&\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{q - 2} (u_n(x) - u_n(y)) (\varphi(x) - \varphi(y))}{|x - y|^{N + s q}} dxdy\\
=\ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u(x) - u(y)|^{q - 2} (u(x) - u(y)) (\varphi(x) - \varphi(y))}{|x - y|^{N + s q}} dxdy.
\end{align*}Finally, it is easy to check that
 \begin{align*}
& \lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} V(\varepsilon x,u_n) |u_n|^{p -2} u_n \varphi dx= \int_{\mathbb{R}^N} V(\varepsilon x,u) |u|^{p -2} u \varphi dx,\\
& \lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} V(\varepsilon x,u_n) |u_n|^{q -2} u_n \varphi dx= \int_{\mathbb{R}^N} V(\varepsilon x,u) |u|^{q -2} u \varphi dx.
\end{align*}
\begin{align*}
& \lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} V(\varepsilon x,u_n) |u_n|^{p -2} u_n \varphi dx= \int_{\mathbb{R}^N} V(\varepsilon x,u) |u|^{p -2} u \varphi dx,\\
& \lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} V(\varepsilon x,u_n) |u_n|^{q -2} u_n \varphi dx= \int_{\mathbb{R}^N} V(\varepsilon x,u) |u|^{q -2} u \varphi dx.
\end{align*} From the above information, together with the fact that ![]() $\langle J_\varepsilon'(u_n),\varphi \rangle \rightarrow 0$ as
$\langle J_\varepsilon'(u_n),\varphi \rangle \rightarrow 0$ as ![]() $n \rightarrow \infty$, it follows that
$n \rightarrow \infty$, it follows that ![]() $\langle J_\varepsilon'(u),\varphi \rangle = 0$ for all
$\langle J_\varepsilon'(u),\varphi \rangle = 0$ for all ![]() $\varphi \in C^\infty_0(\mathbb{R}^N)$. Using the density of
$\varphi \in C^\infty_0(\mathbb{R}^N)$. Using the density of ![]() $C^\infty_0(\mathbb{R}^N)$ in Xɛ, we know that u is a critical point of the functional Jɛ. Consequently,
$C^\infty_0(\mathbb{R}^N)$ in Xɛ, we know that u is a critical point of the functional Jɛ. Consequently, ![]() $\langle J_\varepsilon'(u),u\rangle = 0$.
$\langle J_\varepsilon'(u),u\rangle = 0$.
In order to show that the Palais–Smale sequence satisfies the Palais–Smale condition, we need to establish the following property.
Claim 2: We have
 \begin{align*}
& \limsup_{n \rightarrow \infty} \int_{B_R^c} \left(\int_{\mathbb{R}^N} \left( \frac{|u_n(x) - u_n(y)|^p}{|x - y|^{N + s p}} + \frac{|u_n(x) - u_n(y)|^q}{|x - y|^{N + s q}} \right) dy + V(\varepsilon x) \left(|u_n|^p + |u_n|^q\right) \right) dx\\
&\rightarrow 0 \ \text{as } R \rightarrow + \infty.
\end{align*}
\begin{align*}
& \limsup_{n \rightarrow \infty} \int_{B_R^c} \left(\int_{\mathbb{R}^N} \left( \frac{|u_n(x) - u_n(y)|^p}{|x - y|^{N + s p}} + \frac{|u_n(x) - u_n(y)|^q}{|x - y|^{N + s q}} \right) dy + V(\varepsilon x) \left(|u_n|^p + |u_n|^q\right) \right) dx\\
&\rightarrow 0 \ \text{as } R \rightarrow + \infty.
\end{align*} We first observe that, for all ɛ > 0 small enough, there exists ![]() $ n_0 \in \mathbb{N}$ such that
$ n_0 \in \mathbb{N}$ such that
 \begin{align*}\sup_{n \geqslant n_0} \left|\frac{1}{|x|^\mu} * G(\varepsilon x, u_n)\right|_{L^\infty(\mathbb{R}^N)} \lt \frac{K}{2}.\end{align*}
\begin{align*}\sup_{n \geqslant n_0} \left|\frac{1}{|x|^\mu} * G(\varepsilon x, u_n)\right|_{L^\infty(\mathbb{R}^N)} \lt \frac{K}{2}.\end{align*} For any R > 0, let ![]() $\eta_R \in C^\infty(\mathbb{R}^N)$ be such that
$\eta_R \in C^\infty(\mathbb{R}^N)$ be such that ![]() $0 \leqslant \eta_R \leqslant 1$,
$0 \leqslant \eta_R \leqslant 1$, ![]() $\eta_R = 0$ in
$\eta_R = 0$ in  $B_{\frac{R}{2}}$,
$B_{\frac{R}{2}}$, ![]() $\eta_R = 1$ in
$\eta_R = 1$ in ![]() $B_R^c$, and
$B_R^c$, and ![]() $|\nabla \eta_R| \leqslant C / R$ for some constant C > 0 (which is independent of R). Taking into account the boundedness of the sequence
$|\nabla \eta_R| \leqslant C / R$ for some constant C > 0 (which is independent of R). Taking into account the boundedness of the sequence ![]() $\{\eta_R u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, we see that
$\{\eta_R u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, we see that ![]() $\langle J_\varepsilon'(u_n),\eta_R u_n \rangle \rightarrow 0$ as
$\langle J_\varepsilon'(u_n),\eta_R u_n \rangle \rightarrow 0$ as ![]() $n \rightarrow \infty$. It follows that
$n \rightarrow \infty$. It follows that
 \begin{align*}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^p \eta_R(x)}{|x - y|^{N + s p}} dxdy + \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^q \eta_R(x)}{|x - y|^{N + s q}} dxdy\\
+\ & \int_{\mathbb{R}^N} V(\varepsilon x) \left(|u_n|^p + |u_n|^q\right) \eta_R dx\\
= \ & o_n(1) - \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s p}} dxdy\\
- \ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{q - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s q}} dxdy\\
+ \ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u_n)\right) g(\varepsilon x,u_n) u_n \eta_R dx.
\end{align*}
\begin{align*}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^p \eta_R(x)}{|x - y|^{N + s p}} dxdy + \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^q \eta_R(x)}{|x - y|^{N + s q}} dxdy\\
+\ & \int_{\mathbb{R}^N} V(\varepsilon x) \left(|u_n|^p + |u_n|^q\right) \eta_R dx\\
= \ & o_n(1) - \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s p}} dxdy\\
- \ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{q - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s q}} dxdy\\
+ \ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u_n)\right) g(\varepsilon x,u_n) u_n \eta_R dx.
\end{align*} Fix ɛ > 0 small enough. Let R > 0 sufficiently large such that  $\Lambda_\varepsilon \subset B_{\frac{R}{2}}$. Using the definitions of ηR and K, together with
$\Lambda_\varepsilon \subset B_{\frac{R}{2}}$. Using the definitions of ηR and K, together with ![]() $(g_3)_{ii}$, for
$(g_3)_{ii}$, for ![]() $n \geqslant n_0$ large enough, we have
$n \geqslant n_0$ large enough, we have
 \begin{align}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^p \eta_R(x)}{|x - y|^{N + s p}} dxdy + \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^q \eta_R(x)}{|x - y|^{N + s q}} dxdy\nonumber\\
+ \ & \frac{1}{2} \int_{\mathbb{R}^N} V(\varepsilon x) \left(|u_n|^p + |u_n|^q\right) \eta_R dx\nonumber\\
\leqslant\ & o_n(1) - \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s p}} dxdy\nonumber\\
- \ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{q - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s q}} dxdy.
\end{align}
\begin{align}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^p \eta_R(x)}{|x - y|^{N + s p}} dxdy + \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^q \eta_R(x)}{|x - y|^{N + s q}} dxdy\nonumber\\
+ \ & \frac{1}{2} \int_{\mathbb{R}^N} V(\varepsilon x) \left(|u_n|^p + |u_n|^q\right) \eta_R dx\nonumber\\
\leqslant\ & o_n(1) - \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s p}} dxdy\nonumber\\
- \ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{q - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s q}} dxdy.
\end{align} From the Hölder inequality and the boundedness of the sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, it follows that
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, it follows that
 \begin{align}
& \left| \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s p}} dxdy \right| \nonumber\\
\leqslant \ & C \left(\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\eta_R(x) - \eta_R(y)|^p |u_n(x)|^p}{|x - y|^{N + sp}} dxdy\right)^{\frac{1}{p}}\ (\text{for some constant } C \gt 0).
\end{align}
\begin{align}
& \left| \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s p}} dxdy \right| \nonumber\\
\leqslant \ & C \left(\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\eta_R(x) - \eta_R(y)|^p |u_n(x)|^p}{|x - y|^{N + sp}} dxdy\right)^{\frac{1}{p}}\ (\text{for some constant } C \gt 0).
\end{align} In addition, by the definition of ηR, polar coordinates, and the boundedness of the sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, we have
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, we have
 \begin{align}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\eta_R(x) - \eta_R(y)|^p |u_n(x)|^p}{|x - y|^{N + sp}} dxdy\nonumber\\
\leqslant \ & \int_{\mathbb{R}^N} \int_{|x - y| \gt R} \frac{|\eta_R(x) - \eta_R(y)|^p |u_n(x)|^p}{|x - y|^{N + sp}} dxdy \nonumber\\
&+ \int_{\mathbb{R}^N} \int_{|x - y| \leqslant R} \frac{|\eta_R(x) - \eta_R(y)|^p |u_n(x)|^p}{|x - y|^{N + sp}} dxdy\nonumber\\
\leqslant \ & C \int_{\mathbb{R}^N} \int_{|z| \gt R} \frac{|u_n(x)|^p}{|z|^{N + s p}} dxdz + \frac{C}{R^p} \int_{\mathbb{R}^N} \int_{|z| \leqslant R} \frac{|u_n(x)|^p}{|z|^{N + s p - p}} dxdz\nonumber\\
\leqslant \ & \frac{C}{R^{s p}} \int_{\mathbb{R}^N} |u_n|^p dx + \frac{C}{R^p} R^{- s p + p} \int_{\mathbb{R}^N} |u_n|^p dx\nonumber\\
\leqslant \ & \frac{C}{R^{s p}}.
\end{align}
\begin{align}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\eta_R(x) - \eta_R(y)|^p |u_n(x)|^p}{|x - y|^{N + sp}} dxdy\nonumber\\
\leqslant \ & \int_{\mathbb{R}^N} \int_{|x - y| \gt R} \frac{|\eta_R(x) - \eta_R(y)|^p |u_n(x)|^p}{|x - y|^{N + sp}} dxdy \nonumber\\
&+ \int_{\mathbb{R}^N} \int_{|x - y| \leqslant R} \frac{|\eta_R(x) - \eta_R(y)|^p |u_n(x)|^p}{|x - y|^{N + sp}} dxdy\nonumber\\
\leqslant \ & C \int_{\mathbb{R}^N} \int_{|z| \gt R} \frac{|u_n(x)|^p}{|z|^{N + s p}} dxdz + \frac{C}{R^p} \int_{\mathbb{R}^N} \int_{|z| \leqslant R} \frac{|u_n(x)|^p}{|z|^{N + s p - p}} dxdz\nonumber\\
\leqslant \ & \frac{C}{R^{s p}} \int_{\mathbb{R}^N} |u_n|^p dx + \frac{C}{R^p} R^{- s p + p} \int_{\mathbb{R}^N} |u_n|^p dx\nonumber\\
\leqslant \ & \frac{C}{R^{s p}}.
\end{align}Using (2.13) and (2.14), we see that
 \begin{align}
\left| \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s p}} dxdy \right| \leqslant \frac{C}{R^s}.
\end{align}
\begin{align}
\left| \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{p - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s p}} dxdy \right| \leqslant \frac{C}{R^s}.
\end{align}Also, we have
 \begin{align}
\left| \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{q - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s q}} dxdy \right| \leqslant \frac{C}{R^s}.
\end{align}
\begin{align}
\left| \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|u_n(x) - u_n(y)|^{q - 2} (u_n(x) - u_n(y))(\eta_R(x) - \eta_R(y)) u_n(y)}{|x - y| ^{N + s q}} dxdy \right| \leqslant \frac{C}{R^s}.
\end{align}So, we deduce from (2.12), (2.15), and (2.16) that Claim 2 holds true.
Using Claim 2 and applying the locally compact embedding ![]() $X_\varepsilon \hookrightarrow L^p_{\mathrm{loc}}(\mathbb{R}^N)$, we can derive that
$X_\varepsilon \hookrightarrow L^p_{\mathrm{loc}}(\mathbb{R}^N)$, we can derive that ![]() $u_n \rightarrow u$ in
$u_n \rightarrow u$ in ![]() $L^p(\mathbb{R}^N)$ as
$L^p(\mathbb{R}^N)$ as ![]() $n \rightarrow \infty$. In addition, we deduce from the interpolation inequality that
$n \rightarrow \infty$. In addition, we deduce from the interpolation inequality that ![]() $u_n \rightarrow u$ in
$u_n \rightarrow u$ in ![]() $L^r(\mathbb{R}^N)$ as
$L^r(\mathbb{R}^N)$ as ![]() $n \rightarrow \infty$ for all
$n \rightarrow \infty$ for all ![]() $r \in [p,q_s^*)$. Then, from theorem 4.3 in the study by Lieb–Loss [Reference Lieb and Loss38],
$r \in [p,q_s^*)$. Then, from theorem 4.3 in the study by Lieb–Loss [Reference Lieb and Loss38], ![]() $(g_2)$,
$(g_2)$, ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, the Dominated Convergence Theorem, and the boundedness of the sequence
$(f_2)$, the Dominated Convergence Theorem, and the boundedness of the sequence ![]() $\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, it follows that
$\{u_n\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, it follows that
 \begin{align}
\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u_n)\right) g(\varepsilon x,u_n) u_n dx = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u)\right) g(\varepsilon x,u) u dx.
\end{align}
\begin{align}
\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u_n)\right) g(\varepsilon x,u_n) u_n dx = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u)\right) g(\varepsilon x,u) u dx.
\end{align}Also, we have
 \begin{align*}
& \langle J_\varepsilon'(u_n),u_n\rangle = o_n(1) \ \text{as } n \rightarrow \infty,\\
\Rightarrow\ \ & \|u_n\|_{V_\varepsilon,p}^p + \|u_n\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u_n)\right) g(\varepsilon x,u_n) u_n dx + o_n(1) \ \text{as } n \rightarrow \infty
\end{align*}
\begin{align*}
& \langle J_\varepsilon'(u_n),u_n\rangle = o_n(1) \ \text{as } n \rightarrow \infty,\\
\Rightarrow\ \ & \|u_n\|_{V_\varepsilon,p}^p + \|u_n\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u_n)\right) g(\varepsilon x,u_n) u_n dx + o_n(1) \ \text{as } n \rightarrow \infty
\end{align*}and
 \begin{align*}
& \langle J_\varepsilon'(u),u\rangle = 0,\\
\Rightarrow\ \ & \|u\|_{V_\varepsilon,p}^p + \|u\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u)\right) g(\varepsilon x,u) u dx.
\end{align*}
\begin{align*}
& \langle J_\varepsilon'(u),u\rangle = 0,\\
\Rightarrow\ \ & \|u\|_{V_\varepsilon,p}^p + \|u\|_{V_\varepsilon,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x,u)\right) g(\varepsilon x,u) u dx.
\end{align*}Hence, the above fact and (2.17) imply that
 \begin{align*}\|u_n\|_{V_\varepsilon,p}^p + \|u_n\|_{V_\varepsilon,q}^q = \|u\|_{V_\varepsilon,p}^p + \|u\|_{V_\varepsilon,q}^q + o_n(1) \ \text{as } n \rightarrow \infty.\end{align*}
\begin{align*}\|u_n\|_{V_\varepsilon,p}^p + \|u_n\|_{V_\varepsilon,q}^q = \|u\|_{V_\varepsilon,p}^p + \|u\|_{V_\varepsilon,q}^q + o_n(1) \ \text{as } n \rightarrow \infty.\end{align*}Furthermore, according to lemma 2.10 (a), (b), we see that
 \begin{align*}\|u_n - u\|_{V_\varepsilon,p}^p = \|u_n\|_{V_\varepsilon,p}^p - \|u\|_{V_\varepsilon,p}^p + o_n(1)\end{align*}
\begin{align*}\|u_n - u\|_{V_\varepsilon,p}^p = \|u_n\|_{V_\varepsilon,p}^p - \|u\|_{V_\varepsilon,p}^p + o_n(1)\end{align*}and
 \begin{align*}\|u_n - u\|_{V_\varepsilon,q}^q = \|u_n\|_{V_\varepsilon,q}^q - \|u\|_{V_\varepsilon,q}^q + o_n(1),\end{align*}
\begin{align*}\|u_n - u\|_{V_\varepsilon,q}^q = \|u_n\|_{V_\varepsilon,q}^q - \|u\|_{V_\varepsilon,q}^q + o_n(1),\end{align*} as ![]() $n \rightarrow \infty$. Thus, we conclude that
$n \rightarrow \infty$. Thus, we conclude that
 \begin{align*}\|u_n - u\|_{V_\varepsilon,p}^p + \|u_n - u\|_{V_\varepsilon,q}^q = o_n(1).\end{align*}
\begin{align*}\|u_n - u\|_{V_\varepsilon,p}^p + \|u_n - u\|_{V_\varepsilon,q}^q = o_n(1).\end{align*} This fact means that ![]() $\|u_n - u\|_{X_\varepsilon} \rightarrow 0$ as
$\|u_n - u\|_{X_\varepsilon} \rightarrow 0$ as ![]() $n \rightarrow \infty$. Now, we complete the proof of the lemma.
$n \rightarrow \infty$. Now, we complete the proof of the lemma.
Lemma 2.8. Let ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq).$ Assume that
$\nu \lt (N - \mu) q / (N - sq).$ Assume that ![]() $(f_1)$–
$(f_1)$–![]() $(f_4)$ and
$(f_4)$ and ![]() $(V_1)$–
$(V_1)$–![]() $(V_2)$ are fulfilled, then for all ɛ > 0 small enough, problem (2.2) possesses a non-negative solution
$(V_2)$ are fulfilled, then for all ɛ > 0 small enough, problem (2.2) possesses a non-negative solution ![]() $u_\varepsilon \in {X_\varepsilon}.$
$u_\varepsilon \in {X_\varepsilon}.$
Proof. Using lemmas 2.4 and 2.7, we can employ the Mountain Pass Theorem to infer that for all ɛ > 0 sufficiently small, there exists ![]() $u_\varepsilon \in {X_\varepsilon}$ such that
$u_\varepsilon \in {X_\varepsilon}$ such that ![]() $J_\varepsilon'(u_\varepsilon) = 0$ and
$J_\varepsilon'(u_\varepsilon) = 0$ and ![]() $J_\varepsilon(u_\varepsilon) = c_\varepsilon$. Furthermore, choosing
$J_\varepsilon(u_\varepsilon) = c_\varepsilon$. Furthermore, choosing ![]() $u_\varepsilon^- := \min\{u_\varepsilon,0\}$ and recalling that
$u_\varepsilon^- := \min\{u_\varepsilon,0\}$ and recalling that ![]() $g(\varepsilon \cdot,t) = 0$ for all
$g(\varepsilon \cdot,t) = 0$ for all ![]() $t \leqslant 0$ and
$t \leqslant 0$ and ![]() $\langle J_\varepsilon'(u_\varepsilon),u_\varepsilon^- \rangle = 0$, we can infer that
$\langle J_\varepsilon'(u_\varepsilon),u_\varepsilon^- \rangle = 0$, we can infer that
 \begin{align*}
& \|u_\varepsilon^-\|_{V_\varepsilon,p}^p + \|u_\varepsilon^-\|_{V_\varepsilon,q}^q \leqslant 0,\\
\Rightarrow\ \ & u_\varepsilon^- = 0,\\
\Rightarrow\ \ & u_\varepsilon \geqslant 0 \ \text{and } u_\varepsilon \not\equiv 0.
\end{align*}
\begin{align*}
& \|u_\varepsilon^-\|_{V_\varepsilon,p}^p + \|u_\varepsilon^-\|_{V_\varepsilon,q}^q \leqslant 0,\\
\Rightarrow\ \ & u_\varepsilon^- = 0,\\
\Rightarrow\ \ & u_\varepsilon \geqslant 0 \ \text{and } u_\varepsilon \not\equiv 0.
\end{align*}This ends the proof of the lemma.
Corollary 2.9. Let ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq).$ Then, for all ɛ > 0 sufficiently small, the functional ψɛ satisfies the Palais–Smale condition at the level
$\nu \lt (N - \mu) q / (N - sq).$ Then, for all ɛ > 0 sufficiently small, the functional ψɛ satisfies the Palais–Smale condition at the level ![]() $c \leqslant \vartheta$ on
$c \leqslant \vartheta$ on ![]() $S_\varepsilon^+.$
$S_\varepsilon^+.$
Proof. Let ![]() $\{u_n\}_{n \in \mathbb{N}} \subset S_\varepsilon^+$ be a Palais–Samle sequence for the functional ψɛ at the level c, that is,
$\{u_n\}_{n \in \mathbb{N}} \subset S_\varepsilon^+$ be a Palais–Samle sequence for the functional ψɛ at the level c, that is,
Using lemma 2.3 (c), we see that ![]() $\left\{m_\varepsilon(u_n)\right\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is also a Palais–Samle sequence for the functional Jɛ at the level c. Therefore, we can deduce from lemma 2.7 that the functional Jɛ verifies the Palais–Smale condition. Hence, passing to a subsequence, we can find some
$\left\{m_\varepsilon(u_n)\right\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ is also a Palais–Samle sequence for the functional Jɛ at the level c. Therefore, we can deduce from lemma 2.7 that the functional Jɛ verifies the Palais–Smale condition. Hence, passing to a subsequence, we can find some ![]() $u \in S_\varepsilon^+$ such that
$u \in S_\varepsilon^+$ such that ![]() $m_\varepsilon(u_n) \rightarrow m_\varepsilon(u)$ in Xɛ as
$m_\varepsilon(u_n) \rightarrow m_\varepsilon(u)$ in Xɛ as ![]() $n \rightarrow \infty$. Combining this fact with lemma 2.2 (c), we conclude that
$n \rightarrow \infty$. Combining this fact with lemma 2.2 (c), we conclude that ![]() $u_n \rightarrow u$ in
$u_n \rightarrow u$ in ![]() $S_\varepsilon^+$ as
$S_\varepsilon^+$ as ![]() $n \rightarrow \infty$.
$n \rightarrow \infty$.
We end this section by showing the following result:
Lemma 2.10. Let ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ be a sequence such that
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$ be a sequence such that ![]() $u_n \xrightarrow w u$ in Xɛ, and let
$u_n \xrightarrow w u$ in Xɛ, and let ![]() $\mathcal{A}_t : \mathbb{R} \mapsto \mathbb{R}$ defined by
$\mathcal{A}_t : \mathbb{R} \mapsto \mathbb{R}$ defined by ![]() $\mathcal{A}_t(\tau) = |\tau|^{t - 2} \tau$
$\mathcal{A}_t(\tau) = |\tau|^{t - 2} \tau$ ![]() $(t \in \left\{p,q\right\}).$ Setting
$(t \in \left\{p,q\right\}).$ Setting ![]() $w_n = u_n - u,$ then for all
$w_n = u_n - u,$ then for all ![]() $\varepsilon \geqslant 0$ and
$\varepsilon \geqslant 0$ and ![]() $n \in \mathbb{N}$ large enough, we have
$n \in \mathbb{N}$ large enough, we have
(a)
 $\left([u_n]_{s,p}^p + [u_n]_{s,q}^q \right) - \left([w_n]_{s,p}^p + [w_n]_{s,q}^q \right) - \left([u]_{s,p}^p + [u]_{s,q}^q \right) = o_n(1);$
$\left([u_n]_{s,p}^p + [u_n]_{s,q}^q \right) - \left([w_n]_{s,p}^p + [w_n]_{s,q}^q \right) - \left([u]_{s,p}^p + [u]_{s,q}^q \right) = o_n(1);$(b)
 $\left(\left|V(\varepsilon \cdot)^{1/p} u_n\right|_p^p + \left|V(\varepsilon \cdot)^{1/q} u_n\right|_q^q\right) - \left(\left|V(\varepsilon \cdot)^{1/p} w_n\right|_p^p + \left|V(\varepsilon \cdot)^{1/q} w_n\right|_q^q\right) -\left(\left|V(\varepsilon \cdot)^{1/p} u\right|_p^p + \left|V(\varepsilon \cdot)^{1/q} u\right|_q^q\right) = o_n(1);$
$\left(\left|V(\varepsilon \cdot)^{1/p} u_n\right|_p^p + \left|V(\varepsilon \cdot)^{1/q} u_n\right|_q^q\right) - \left(\left|V(\varepsilon \cdot)^{1/p} w_n\right|_p^p + \left|V(\varepsilon \cdot)^{1/q} w_n\right|_q^q\right) -\left(\left|V(\varepsilon \cdot)^{1/p} u\right|_p^p + \left|V(\varepsilon \cdot)^{1/q} u\right|_q^q\right) = o_n(1);$(c)
 $\left| \mathcal{A}_p(u_n)- \mathcal{A}_p(w_n) - \mathcal{A}_p(u) \right|_{{\frac{p}{p - 1}}}^{\frac{p}{p - 1}}+\left| \mathcal{A}_q(u_n)- \mathcal{A}_q(w_n) - \mathcal{A}_q(u) \right|_{{\frac{q}{q - 1}}}^{\frac{q}{q - 1}} = o_n(1);$
$\left| \mathcal{A}_p(u_n)- \mathcal{A}_p(w_n) - \mathcal{A}_p(u) \right|_{{\frac{p}{p - 1}}}^{\frac{p}{p - 1}}+\left| \mathcal{A}_q(u_n)- \mathcal{A}_q(w_n) - \mathcal{A}_q(u) \right|_{{\frac{q}{q - 1}}}^{\frac{q}{q - 1}} = o_n(1);$(d)
 $\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \Bigg|\frac{\mathcal{A}_p(u_n(x) - u_n(y))}{|x - y|^{\frac{N + sp}{p / (p - 1)}}} - \frac{\mathcal{A}_p(w_n(x) - w_n(y))}{|x - y|^{\frac{N + sp}{p / (p - 1)}}} - \frac{\mathcal{A}_p(u(x) - u(y))}{|x - y|^{\frac{N + sp}{p / (p - 1)}}} \Bigg|^{\frac{p}{p - 1}}dxdy$
$\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \Bigg|\frac{\mathcal{A}_p(u_n(x) - u_n(y))}{|x - y|^{\frac{N + sp}{p / (p - 1)}}} - \frac{\mathcal{A}_p(w_n(x) - w_n(y))}{|x - y|^{\frac{N + sp}{p / (p - 1)}}} - \frac{\mathcal{A}_p(u(x) - u(y))}{|x - y|^{\frac{N + sp}{p / (p - 1)}}} \Bigg|^{\frac{p}{p - 1}}dxdy$ $ + \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \Bigg|\frac{\mathcal{A}_q(u_n(x) - u_n(y))}{|x - y|^{\frac{N + sq}{q / (q - 1)}}} - \frac{\mathcal{A}_q(w_n(x) - w_n(y))}{|x - y|^{\frac{N + sq}{q / (q - 1)}}} - \frac{\mathcal{A}_q(u(x) - u(y))}{|x - y|^{\frac{N + sq}{q / (q - 1)}}} \Bigg|^{\frac{q}{q - 1}}dxdy$
$ + \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \Bigg|\frac{\mathcal{A}_q(u_n(x) - u_n(y))}{|x - y|^{\frac{N + sq}{q / (q - 1)}}} - \frac{\mathcal{A}_q(w_n(x) - w_n(y))}{|x - y|^{\frac{N + sq}{q / (q - 1)}}} - \frac{\mathcal{A}_q(u(x) - u(y))}{|x - y|^{\frac{N + sq}{q / (q - 1)}}} \Bigg|^{\frac{q}{q - 1}}dxdy$ $ = o_n(1);$
$ = o_n(1);$(e)
 $\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) F(u_n) dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) F(w_n) dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u)\right) F(u) dx = o_n(1)$
$\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) F(u_n) dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) F(w_n) dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u)\right) F(u) dx = o_n(1)$
and for any ![]() $\varphi \in {X_\varepsilon}$ with
$\varphi \in {X_\varepsilon}$ with ![]() $\|\varphi\|_{X_\varepsilon} \leqslant 1$, it holds
$\|\varphi\|_{X_\varepsilon} \leqslant 1$, it holds
(f)
 $\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) f(u_n) \varphi dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) f(w_n) \varphi dx
- \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) \varphi dx = o_n(1).$
$\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) f(u_n) \varphi dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) f(w_n) \varphi dx
- \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) \varphi dx = o_n(1).$
Proof. We first point out that the proofs of (a) and (b) follow from the Brezis–Lieb Lemma (see [Reference Brezis and Lieb17]). Moreover, arguing as in the proof lemma 3.2 of Mercuri and Willem [Reference Mercuri and Willem43], we see that (c) holds true.
Next, we give the details of the proofs of (d), (e), and (f) for the convenience of readers.
(d) Case 1: ![]() $2 \leqslant t \in \left\{p,q\right\}$.
$2 \leqslant t \in \left\{p,q\right\}$.
We deduce from the Mean Value Theorem, the Young inequality, and ![]() $t \geqslant 2$ that for any fixed σ > 0, there exists
$t \geqslant 2$ that for any fixed σ > 0, there exists ![]() $C_\sigma \gt 0$ such that
$C_\sigma \gt 0$ such that
 \begin{align}
\left||a + b|^{t - 2}(a + b) - \left|a\right|^{t - 2} a\right| \leqslant \sigma |a|^{t - 1} + C_\sigma |b|^{t - 1} \quad \ \text{for all } a,\ b \in \mathbb{R}.
\end{align}
\begin{align}
\left||a + b|^{t - 2}(a + b) - \left|a\right|^{t - 2} a\right| \leqslant \sigma |a|^{t - 1} + C_\sigma |b|^{t - 1} \quad \ \text{for all } a,\ b \in \mathbb{R}.
\end{align}In (2.18), we take
 \begin{align*}a = \frac{w_n(x) - w_n(y)}{|x - y|^{\frac{N + s t}{t}}} \quad \ \text{and }\quad b = \frac{u(x) - u(y)}{|x - y|^{\frac{N + s t}{t}}},\end{align*}
\begin{align*}a = \frac{w_n(x) - w_n(y)}{|x - y|^{\frac{N + s t}{t}}} \quad \ \text{and }\quad b = \frac{u(x) - u(y)}{|x - y|^{\frac{N + s t}{t}}},\end{align*}and we have
 \begin{align*}
\Bigg| \frac{\mathcal{A}_t( u_n(x) - u_n(y))}{|x - y|^{\frac{N + s t}{t / (t - 1)}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + s t}{t / (t - 1)}}}\Bigg| & \leqslant\sigma \frac{|w_n(x) - w_n(y)|^{t - 1}}{|x - y|^{\frac{N + s t}{t / (t - 1)}}} \\
& \quad + C_\sigma \frac{|u(x) - u(y)|^{t - 1}}{|x - y|^{\frac{N + s t}{t / (t - 1)}}} .
\end{align*}
\begin{align*}
\Bigg| \frac{\mathcal{A}_t( u_n(x) - u_n(y))}{|x - y|^{\frac{N + s t}{t / (t - 1)}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + s t}{t / (t - 1)}}}\Bigg| & \leqslant\sigma \frac{|w_n(x) - w_n(y)|^{t - 1}}{|x - y|^{\frac{N + s t}{t / (t - 1)}}} \\
& \quad + C_\sigma \frac{|u(x) - u(y)|^{t - 1}}{|x - y|^{\frac{N + s t}{t / (t - 1)}}} .
\end{align*} Now, we introduce the mapping  $H_{\sigma,n}^1 : \mathbb{R}^{2 N} \mapsto \mathbb{R}_+$ given by
$H_{\sigma,n}^1 : \mathbb{R}^{2 N} \mapsto \mathbb{R}_+$ given by
 \begin{align*}
&H_{\sigma,n}^1(x,y) := \max\Bigg\{\left|\frac{\mathcal{A}_t(u_n(x) - u_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(u(x) - u(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}}\right|\\
&- \sigma \frac{|w_n(x) - w_n(y)|^{t - 1}}{|x - y|^{\frac{N + s t}{t / (t - 1)}}},0 \Bigg\}.
\end{align*}
\begin{align*}
&H_{\sigma,n}^1(x,y) := \max\Bigg\{\left|\frac{\mathcal{A}_t(u_n(x) - u_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(u(x) - u(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}}\right|\\
&- \sigma \frac{|w_n(x) - w_n(y)|^{t - 1}}{|x - y|^{\frac{N + s t}{t / (t - 1)}}},0 \Bigg\}.
\end{align*} Then,  $H_{\sigma,n}^1(x,y) \rightarrow 0$ a.e. in
$H_{\sigma,n}^1(x,y) \rightarrow 0$ a.e. in ![]() $\mathbb{R}^{2 N}$ as
$\mathbb{R}^{2 N}$ as ![]() $n \rightarrow \infty$ and
$n \rightarrow \infty$ and
 \begin{align*}0 \leqslant H_{\sigma,n}^1(x,y) \leqslant C \frac{|u(x) - u(y)|^{t - 1}}{|x - y|^{\frac{N + s t}{t / (t - 1)}}} \in L^{\frac{t}{t - 1}}(\mathbb{R}^{2 N})\end{align*}
\begin{align*}0 \leqslant H_{\sigma,n}^1(x,y) \leqslant C \frac{|u(x) - u(y)|^{t - 1}}{|x - y|^{\frac{N + s t}{t / (t - 1)}}} \in L^{\frac{t}{t - 1}}(\mathbb{R}^{2 N})\end{align*}for some constant C > 0. Hence, from the Dominated Convergence Theorem, we obtain
 \begin{align*}\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \left|H_{\sigma,n}^1\right|^{\frac{t}{t - 1}} dxdy \rightarrow 0 \ \text{in } \mathbb{R} \ \text{as } n \rightarrow \infty.\end{align*}
\begin{align*}\int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \left|H_{\sigma,n}^1\right|^{\frac{t}{t - 1}} dxdy \rightarrow 0 \ \text{in } \mathbb{R} \ \text{as } n \rightarrow \infty.\end{align*} In addition, according to the definition of  $H_{\sigma,n}^1$, we have
$H_{\sigma,n}^1$, we have
 \begin{align*}
& \left|\frac{\mathcal{A}_t(u_n(x) - u_n(y))}{|x - y|^{\frac{N + st}{(t / (t - 1))}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + st}{(t / (t - 1))}}} - \frac{\mathcal{A}_t(u(x) - u(y))}{|x - y|^{\frac{N + st}{(t / (t - 1))}}}\right|^\frac{t}{t - 1} \\
\leqslant\ & C \left(\sigma^\frac{t}{t - 1} \frac{|w_n(x) - w_n(y)|^t}{|x - y|^{N + s t}} + (H_{\sigma,n}^1(x,y))^\frac{t}{t - 1}\right)
\end{align*}
\begin{align*}
& \left|\frac{\mathcal{A}_t(u_n(x) - u_n(y))}{|x - y|^{\frac{N + st}{(t / (t - 1))}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + st}{(t / (t - 1))}}} - \frac{\mathcal{A}_t(u(x) - u(y))}{|x - y|^{\frac{N + st}{(t / (t - 1))}}}\right|^\frac{t}{t - 1} \\
\leqslant\ & C \left(\sigma^\frac{t}{t - 1} \frac{|w_n(x) - w_n(y)|^t}{|x - y|^{N + s t}} + (H_{\sigma,n}^1(x,y))^\frac{t}{t - 1}\right)
\end{align*}for some constant C > 0. This implies that
 \begin{align*} & \quad \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \left|\frac{\mathcal{A}_t(u_n(x) - u_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(u(x) - u(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} \right|^{\frac{t}{t - 1}}dxdy\\
& = o_n(1)\end{align*}
\begin{align*} & \quad \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \left|\frac{\mathcal{A}_t(u_n(x) - u_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(u(x) - u(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} \right|^{\frac{t}{t - 1}}dxdy\\
& = o_n(1)\end{align*} holds true for ![]() $n \in \mathbb{N}$ large enough.
$n \in \mathbb{N}$ large enough.
Case 2: ![]() $1 \lt t \lt 2$.
$1 \lt t \lt 2$.
Invoking lemma 3.1 in the study by Mercuri and Willem [Reference Mercuri and Willem43] and applying the Dominated Convergence Theorem, for ![]() $n \in \mathbb{N}$ large enough, we obtain that
$n \in \mathbb{N}$ large enough, we obtain that
 \begin{align*} & \quad \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \left|\frac{\mathcal{A}_t(u_n(x) - u_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(u(x) - u(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} \right|^{\frac{t}{t - 1}}dxdy \\
& = o_n(1)\end{align*}
\begin{align*} & \quad \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \left|\frac{\mathcal{A}_t(u_n(x) - u_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(w_n(x) - w_n(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} - \frac{\mathcal{A}_t(u(x) - u(y))}{|x - y|^{\frac{N + st}{t / (t - 1)}}} \right|^{\frac{t}{t - 1}}dxdy \\
& = o_n(1)\end{align*}holds true.
Now, combining Case 1 and Case 2, we complete the proof of (d).
(e) Using the Mean Value Theorem, hypotheses ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, and Young’s inequality, we can infer that for any σ > 0, there exists
$(f_2)$, and Young’s inequality, we can infer that for any σ > 0, there exists ![]() $C_\sigma \gt 0$ such that
$C_\sigma \gt 0$ such that
 \begin{align*}\left|F(u_n) - F(w_n) -F(u)\right|^{\frac{2 N }{2 N - \mu}} & \leqslant \sigma \left(|u_n|^{\frac{2 N p }{2 N - \mu}} + |u_n|^{\frac{2 N \nu}{2 N - \mu}} \right) \\
& \quad + C_\sigma\left(|u|^{\frac{2 N p }{2 N - \mu}} + |u|^{\frac{2 N \nu}{2 N - \mu}}\right).\end{align*}
\begin{align*}\left|F(u_n) - F(w_n) -F(u)\right|^{\frac{2 N }{2 N - \mu}} & \leqslant \sigma \left(|u_n|^{\frac{2 N p }{2 N - \mu}} + |u_n|^{\frac{2 N \nu}{2 N - \mu}} \right) \\
& \quad + C_\sigma\left(|u|^{\frac{2 N p }{2 N - \mu}} + |u|^{\frac{2 N \nu}{2 N - \mu}}\right).\end{align*}Define the following mapping:
 \begin{align*}H_{\sigma,n}^2 := \max\left\{\left|F(u_n) - F(w_n) -F(u)\right|^{\frac{2 N }{2 N - \mu}} - \sigma \left(|u_n|^{\frac{2 N p }{2 N - \mu}} + |u_n|^{\frac{2 N \nu}{2 N - \mu}} \right),0\right\}.\end{align*}
\begin{align*}H_{\sigma,n}^2 := \max\left\{\left|F(u_n) - F(w_n) -F(u)\right|^{\frac{2 N }{2 N - \mu}} - \sigma \left(|u_n|^{\frac{2 N p }{2 N - \mu}} + |u_n|^{\frac{2 N \nu}{2 N - \mu}} \right),0\right\}.\end{align*} Then, arguing as in the proof of lemma 2.10 (d) and using the boundedness of the sequence ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, for
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, for ![]() $n \in \mathbb{N}$ sufficiently large, we can derive that
$n \in \mathbb{N}$ sufficiently large, we can derive that
 \begin{align}
\int_{\mathbb{R}^N}\left|F(u_n) - F(w_n) -F(u)\right|^{\frac{2 N }{2 N - \mu}} dx = o_n(1).
\end{align}
\begin{align}
\int_{\mathbb{R}^N}\left|F(u_n) - F(w_n) -F(u)\right|^{\frac{2 N }{2 N - \mu}} dx = o_n(1).
\end{align}On the other hand, we can deduce from theorem 4.3 in the study by Lieb and Loss [Reference Lieb and Loss38] that
 \begin{align}
\int_{\mathbb{R}^N}\left|\frac{1}{|x|^\mu} *\left( F(u_n) - F(w_n) - F(u)\right)\right|^{\frac{2 N }{\mu}} dx = o_n(1)
\end{align}
\begin{align}
\int_{\mathbb{R}^N}\left|\frac{1}{|x|^\mu} *\left( F(u_n) - F(w_n) - F(u)\right)\right|^{\frac{2 N }{\mu}} dx = o_n(1)
\end{align} for ![]() $n \in \mathbb{N}$ large enough.
$n \in \mathbb{N}$ large enough.
We note that
 \begin{align*}
&\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) F(u_n) dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) F(w_n) dx\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * \left(F(u_n) - F(w_n)\right)\right) \left(F(u_n) - F(w_n)\right) dx \\
+ \ & 2 \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * \left(F(u_n) - F(w_n)\right)\right) F(w_n) dx.
\end{align*}
\begin{align*}
&\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) F(u_n) dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) F(w_n) dx\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * \left(F(u_n) - F(w_n)\right)\right) \left(F(u_n) - F(w_n)\right) dx \\
+ \ & 2 \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * \left(F(u_n) - F(w_n)\right)\right) F(w_n) dx.
\end{align*} Using the above equality and taking into account that ![]() $F(w_n) \xrightarrow w 0$ in
$F(w_n) \xrightarrow w 0$ in  $L^{\frac{2 N }{2 N - \mu}}(\mathbb{R}^N)$ as
$L^{\frac{2 N }{2 N - \mu}}(\mathbb{R}^N)$ as ![]() $n \rightarrow \infty$, together with (2.19)–(2.20), we can show that (e) holds true.
$n \rightarrow \infty$, together with (2.19)–(2.20), we can show that (e) holds true.
(f) We first prove that
 \begin{align}
\sup_{\|\varphi\|_{X_\varepsilon} \leqslant 1} \int_{\mathbb{R}^N} \left|\left(f(u_n) - f(w_n) - f(u)\right) \varphi\right|^{\frac{2 N }{2 N - \mu}} dx = o_n(1)
\end{align}
\begin{align}
\sup_{\|\varphi\|_{X_\varepsilon} \leqslant 1} \int_{\mathbb{R}^N} \left|\left(f(u_n) - f(w_n) - f(u)\right) \varphi\right|^{\frac{2 N }{2 N - \mu}} dx = o_n(1)
\end{align} for ![]() $n \in \mathbb{N}$ large enough.
$n \in \mathbb{N}$ large enough.
For any fixed ![]() $0 \lt \sigma \lt 1$, we deduce from hypothesis
$0 \lt \sigma \lt 1$, we deduce from hypothesis ![]() $(f_1)$ that there exists
$(f_1)$ that there exists ![]() $0 \lt \lambda_0 := \lambda_0(\sigma) \lt 1$ such that
$0 \lt \lambda_0 := \lambda_0(\sigma) \lt 1$ such that
In addition, by hypothesis ![]() $(f_2)$, we can find
$(f_2)$, we can find ![]() $\lambda_1 := \lambda_1(\sigma) \gt 2$ such that
$\lambda_1 := \lambda_1(\sigma) \gt 2$ such that
Next, by the continuity of f, there is a positive constant ![]() $\gamma :=\gamma(\sigma) \lt \lambda_0$ such that
$\gamma :=\gamma(\sigma) \lt \lambda_0$ such that
 \begin{align}
|f(t_1) - f(t_2)| \leqslant \lambda_0^{p - 1} \sigma \quad \ \text{for all } |t_1 - t_2| \leqslant \gamma,\ |t_1|,\, |t_2| \leqslant \lambda_1 + 1.
\end{align}
\begin{align}
|f(t_1) - f(t_2)| \leqslant \lambda_0^{p - 1} \sigma \quad \ \text{for all } |t_1 - t_2| \leqslant \gamma,\ |t_1|,\, |t_2| \leqslant \lambda_1 + 1.
\end{align} Additionally, combining ![]() $(f_1)$ and
$(f_1)$ and ![]() $(f_2)$, we can conclude that there exists
$(f_2)$, we can conclude that there exists ![]() $C(\sigma) \gt 0$ such that
$C(\sigma) \gt 0$ such that
We now estimate the following term:
 \begin{align*}\int_{\mathbb{R}^N \setminus B_R}\left|(f(u_n) - f(w_n) - f(u))\varphi\right|^{\frac{2 N}{2 N - \mu}} dx.\end{align*}
\begin{align*}\int_{\mathbb{R}^N \setminus B_R}\left|(f(u_n) - f(w_n) - f(u))\varphi\right|^{\frac{2 N}{2 N - \mu}} dx.\end{align*} Since ![]() $u \in {X_\varepsilon}$, together with (2.25), the Hölder inequality (2.1), and
$u \in {X_\varepsilon}$, together with (2.25), the Hölder inequality (2.1), and ![]() $(V_1)$, we know that there exists
$(V_1)$, we know that there exists ![]() $R = R(\sigma) \gt 0$ such that
$R = R(\sigma) \gt 0$ such that
 \begin{align}
& \quad \int_{\mathbb{R}^N \setminus B_R} \left|f(u) \varphi\right|^{\frac{2 N}{2 N - \mu}} dx \nonumber\\
& \leqslant C \left(\int_{\mathbb{R}^N \setminus B_R} |u|^{\frac{2 N (p - 1)}{2 N - \mu}} |\varphi|^{\frac{2 N}{2 N - \mu}} dx + \int_{\mathbb{R}^N \setminus B_R} |u|^{\frac{2 N (\nu - 1)}{2 N - \mu}} |\varphi|^{\frac{2 N}{2 N - \mu}} dx \right)\nonumber\\
&\leqslant C \left(\left(\int_{\mathbb{R}^N \setminus B_R} |u|^{\frac{2 Np}{2 N - \mu}} dx\right)^{\frac{p - 1}{p}} + \left(\int_{\mathbb{R}^N \setminus B_R} |u|^{\frac{2 N \nu}{2 N - \mu}} \right)^{\frac{\nu - 1}{\nu}} \right)\|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}\nonumber\\
& \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}
\begin{align}
& \quad \int_{\mathbb{R}^N \setminus B_R} \left|f(u) \varphi\right|^{\frac{2 N}{2 N - \mu}} dx \nonumber\\
& \leqslant C \left(\int_{\mathbb{R}^N \setminus B_R} |u|^{\frac{2 N (p - 1)}{2 N - \mu}} |\varphi|^{\frac{2 N}{2 N - \mu}} dx + \int_{\mathbb{R}^N \setminus B_R} |u|^{\frac{2 N (\nu - 1)}{2 N - \mu}} |\varphi|^{\frac{2 N}{2 N - \mu}} dx \right)\nonumber\\
&\leqslant C \left(\left(\int_{\mathbb{R}^N \setminus B_R} |u|^{\frac{2 Np}{2 N - \mu}} dx\right)^{\frac{p - 1}{p}} + \left(\int_{\mathbb{R}^N \setminus B_R} |u|^{\frac{2 N \nu}{2 N - \mu}} \right)^{\frac{\nu - 1}{\nu}} \right)\|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}\nonumber\\
& \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}for some constant C > 0.
Let us define
 \begin{align*}D_{u_n}^1 := \left\{x \in \mathbb{R}^N \setminus B_R : |u_n(x)| \leqslant \lambda_0\right\}.\end{align*}
\begin{align*}D_{u_n}^1 := \left\{x \in \mathbb{R}^N \setminus B_R : |u_n(x)| \leqslant \lambda_0\right\}.\end{align*} According to (2.22), the Hölder inequality, (2.1), ![]() $(V_1)$, and the boundedness of the sequence
$(V_1)$, and the boundedness of the sequence ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, we have
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_\varepsilon}$, we have
 \begin{align}
&\int_{D_{u_n}^1 \cap |u| \leqslant \gamma} |(f(u_n) - f(w_n))\varphi|^{\frac{2 N}{2 N- \mu}} dx \nonumber\\
\leqslant\ & \int_{D_{u_n}^1 \cap |u|
\leqslant \gamma} \left( \sigma |u_n|^{p - 1} + \sigma |w_n|^{p - 1}\right)^\frac{2 N}{2 N - \mu}|\varphi|^{\frac{2 N}{2 N - \mu}} dx\nonumber\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}
\begin{align}
&\int_{D_{u_n}^1 \cap |u| \leqslant \gamma} |(f(u_n) - f(w_n))\varphi|^{\frac{2 N}{2 N- \mu}} dx \nonumber\\
\leqslant\ & \int_{D_{u_n}^1 \cap |u|
\leqslant \gamma} \left( \sigma |u_n|^{p - 1} + \sigma |w_n|^{p - 1}\right)^\frac{2 N}{2 N - \mu}|\varphi|^{\frac{2 N}{2 N - \mu}} dx\nonumber\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}for some constant C > 0.
Set
 \begin{align*}D_{u_n}^2 := \left\{x \in \mathbb{R}^N \setminus B_R : |u_n(x)| \geqslant \lambda_1\right\}.\end{align*}
\begin{align*}D_{u_n}^2 := \left\{x \in \mathbb{R}^N \setminus B_R : |u_n(x)| \geqslant \lambda_1\right\}.\end{align*}Arguing as in (2.27), together with (2.23), we can obtain
 \begin{align}
&\int_{D_{u_n}^2 \cap |u| \leqslant \gamma} |(f(u_n) - f(w_n))\varphi|^{\frac{2 N}{2 N- \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}.
\end{align}
\begin{align}
&\int_{D_{u_n}^2 \cap |u| \leqslant \gamma} |(f(u_n) - f(w_n))\varphi|^{\frac{2 N}{2 N- \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}.
\end{align}for some positive constant C > 0.
Now, we introduce the following set:
 \begin{align*}D_{u_n}^3 := \left\{x \in \mathbb{R}^N \setminus B_R : \lambda_0 \leqslant |u_n(x)| \leqslant \lambda_1\right\}.\end{align*}
\begin{align*}D_{u_n}^3 := \left\{x \in \mathbb{R}^N \setminus B_R : \lambda_0 \leqslant |u_n(x)| \leqslant \lambda_1\right\}.\end{align*} It is easy to check that  $|D_{u_n}^3| \lt + \infty$, since
$|D_{u_n}^3| \lt + \infty$, since ![]() $u_n \in {X_\varepsilon}$. So, from (2.24), it follows that
$u_n \in {X_\varepsilon}$. So, from (2.24), it follows that
 \begin{align}
&\int_{D_{u_n}^3 \cap |u| \leqslant \gamma} |(f(u_n) - f(w_n))\varphi|^{\frac{2 N}{2 N- \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}
\begin{align}
&\int_{D_{u_n}^3 \cap |u| \leqslant \gamma} |(f(u_n) - f(w_n))\varphi|^{\frac{2 N}{2 N- \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}for some constant C > 0.
Thus, we deduce from (2.27)–(2.29) that
 \begin{align}
\int_{(\mathbb{R}^N \setminus B_R) \cap |u| \leqslant \gamma}\left|(f(u_n) - f(w_n))\varphi\right|^{\frac{2 N}{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} \quad \ \text{for all } n \in \mathbb{N}.
\end{align}
\begin{align}
\int_{(\mathbb{R}^N \setminus B_R) \cap |u| \leqslant \gamma}\left|(f(u_n) - f(w_n))\varphi\right|^{\frac{2 N}{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} \quad \ \text{for all } n \in \mathbb{N}.
\end{align} Thanks to ![]() $u \in {X_\varepsilon}$, we have
$u \in {X_\varepsilon}$, we have ![]() $|(\mathbb{R}^N \setminus B_R) \cap \{|u| \geqslant \gamma\}| \rightarrow 0$ as
$|(\mathbb{R}^N \setminus B_R) \cap \{|u| \geqslant \gamma\}| \rightarrow 0$ as ![]() $R \rightarrow \infty$. Using (2.25) again, we deduce that there exists
$R \rightarrow \infty$. Using (2.25) again, we deduce that there exists ![]() $R := R(\sigma) \gt 0$ such that
$R := R(\sigma) \gt 0$ such that
 \begin{align*}
&\int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} |(f(u_n) - f(w_n)) \varphi|^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & \int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} \left(\sigma \left(|u_n|^{\nu - 1} + |w_n|^{\nu - 1}\right)|\varphi| + C(\sigma)\left(|u_n|^{p - 1} + |w_n|^{p - 1}\right)|\varphi|\right)^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C \int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} \left(C(\sigma)\left(|u_n|^{p - 1} + |w_n|^{p - 1}\right)|\varphi|\right)^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + (2C(\sigma))^{\frac{2 N}{2 N - \mu}} \int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} \left(|u_n|^{\frac{2 N (p - 1)}{2 N - \mu}} + |w_n|^{\frac{2 N(p - 1)}{2 N - \mu}}\right)|\varphi|^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C(C (\sigma))^{\frac{2 N}{2 N - \mu}} \left(\int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} |\varphi|^{\frac{2 N p}{2 N - \mu}} dx\right)^{\frac{1}{p}}\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C(C (\sigma))^{\frac{2 N}{2 N - \mu}} \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} |(\mathbb{R}^N \setminus B_R) \cap \{|u| \geqslant \gamma\}|^{\frac{2 s p - \mu}{p (2 N - \mu)}}\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align*}
\begin{align*}
&\int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} |(f(u_n) - f(w_n)) \varphi|^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & \int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} \left(\sigma \left(|u_n|^{\nu - 1} + |w_n|^{\nu - 1}\right)|\varphi| + C(\sigma)\left(|u_n|^{p - 1} + |w_n|^{p - 1}\right)|\varphi|\right)^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C \int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} \left(C(\sigma)\left(|u_n|^{p - 1} + |w_n|^{p - 1}\right)|\varphi|\right)^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + (2C(\sigma))^{\frac{2 N}{2 N - \mu}} \int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} \left(|u_n|^{\frac{2 N (p - 1)}{2 N - \mu}} + |w_n|^{\frac{2 N(p - 1)}{2 N - \mu}}\right)|\varphi|^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C(C (\sigma))^{\frac{2 N}{2 N - \mu}} \left(\int_{(\mathbb{R}^N \setminus B_R) \cap |u| \geqslant \gamma} |\varphi|^{\frac{2 N p}{2 N - \mu}} dx\right)^{\frac{1}{p}}\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C(C (\sigma))^{\frac{2 N}{2 N - \mu}} \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} |(\mathbb{R}^N \setminus B_R) \cap \{|u| \geqslant \gamma\}|^{\frac{2 s p - \mu}{p (2 N - \mu)}}\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align*} where C is a positive constant. Combining this inequality with (2.26) and (2.30), we deduce that there is a constant C > 0 such that for all ![]() $n \in \mathbb{N}$,
$n \in \mathbb{N}$,
 \begin{align}
\int_{\mathbb{R}^N \setminus B_R} \left|(f(u_n) - f(w_n) - f(u)) \varphi\right|^{\frac{2 N}{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}.
\end{align}
\begin{align}
\int_{\mathbb{R}^N \setminus B_R} \left|(f(u_n) - f(w_n) - f(u)) \varphi\right|^{\frac{2 N}{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}.
\end{align} Recalling that ![]() $u_n \xrightarrow w u$ in Xɛ as
$u_n \xrightarrow w u$ in Xɛ as ![]() $n \rightarrow \infty$ and passing to a subsequence (still denoted by
$n \rightarrow \infty$ and passing to a subsequence (still denoted by ![]() $\left\{u_n\right\}_{n \in \mathbb{N}}$), we can assume that
$\left\{u_n\right\}_{n \in \mathbb{N}}$), we can assume that ![]() $u_n \rightarrow u$ strongly in
$u_n \rightarrow u$ strongly in  $L^{\frac{2 N p}{2 N - \mu}}(B_R)$ (since
$L^{\frac{2 N p}{2 N - \mu}}(B_R)$ (since ![]() $0 \lt \mu \lt 2 sp$) and there is a function
$0 \lt \mu \lt 2 sp$) and there is a function  $d \in L^{\frac{2 N p}{2 N - \mu}}(B_R)$ such that
$d \in L^{\frac{2 N p}{2 N - \mu}}(B_R)$ such that ![]() $|u_n(x)|$,
$|u_n(x)|$, ![]() $|u(x)| \leqslant d(x)$ a.e.
$|u(x)| \leqslant d(x)$ a.e. ![]() $x \in B_R$.
$x \in B_R$.
For ![]() $n \in \mathbb{N}$ large enough, we have
$n \in \mathbb{N}$ large enough, we have
 \begin{align}
\int_{B_R} |f(w_n) \varphi|^{\frac{2 N}{2 N - \mu}} & dx \leqslant \int_{B_R} \left( C(\sigma) |w_n)|^{p - 1} + \sigma |w_n|^{\nu - 1}\right)^{\frac{2 N}{2 N - \mu}} |\varphi|^{\frac{2 N}{2 N - \mu}}dx\nonumber\\
&\leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + (2C(\sigma))^{\frac{2 N}{2 N - \mu}} \left(\int_{B_R}|w_n|^{\frac{2 N p}{2 N - \mu}}\right)^{\frac{p - 1}{p}} |\varphi|_{\frac{2 N p}{2 N - p}}^{\frac{2 N}{2 N - \mu}}\nonumber\\
& \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align}
\begin{align}
\int_{B_R} |f(w_n) \varphi|^{\frac{2 N}{2 N - \mu}} & dx \leqslant \int_{B_R} \left( C(\sigma) |w_n)|^{p - 1} + \sigma |w_n|^{\nu - 1}\right)^{\frac{2 N}{2 N - \mu}} |\varphi|^{\frac{2 N}{2 N - \mu}}dx\nonumber\\
&\leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + (2C(\sigma))^{\frac{2 N}{2 N - \mu}} \left(\int_{B_R}|w_n|^{\frac{2 N p}{2 N - \mu}}\right)^{\frac{p - 1}{p}} |\varphi|_{\frac{2 N p}{2 N - p}}^{\frac{2 N}{2 N - \mu}}\nonumber\\
& \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align}where C > 0 is some constant.
Set  $D_{u_n}^4 :=\left\{x \in B_R : |u_n(x) - u(x)| \geqslant 1\right\}$. So, we get
$D_{u_n}^4 :=\left\{x \in B_R : |u_n(x) - u(x)| \geqslant 1\right\}$. So, we get
 \begin{align*}
&\int_{D_{u_n}^4} |(f(u_n) - f(u))\varphi|^{\frac{2 N}{2 N - \mu}} dx \\
\leqslant \ & \int_{D_{u_n}^4} \left(C(\sigma) (|u_n|^{p - 1} + |u|^{p - 1}) +\sigma (|u_n|^{\nu - 1} + |u|^{\nu - 1})\right)^{\frac{2 N}{2 N - \mu}} |\varphi|^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C(2 C(\sigma))^{\frac{2 N}{2 N - \mu}} \left(\int_{D_{u_n}^4} d^{\frac{2 N p}{2 N - \mu}} dx\right)^\frac{p - 1}{p} \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align*}
\begin{align*}
&\int_{D_{u_n}^4} |(f(u_n) - f(u))\varphi|^{\frac{2 N}{2 N - \mu}} dx \\
\leqslant \ & \int_{D_{u_n}^4} \left(C(\sigma) (|u_n|^{p - 1} + |u|^{p - 1}) +\sigma (|u_n|^{\nu - 1} + |u|^{\nu - 1})\right)^{\frac{2 N}{2 N - \mu}} |\varphi|^{\frac{2 N}{2 N - \mu}} dx\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C(2 C(\sigma))^{\frac{2 N}{2 N - \mu}} \left(\int_{D_{u_n}^4} d^{\frac{2 N p}{2 N - \mu}} dx\right)^\frac{p - 1}{p} \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align*} where C > 0 is some constant. We observe that  $|D_{u_n}^4| \rightarrow 0$ in
$|D_{u_n}^4| \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$, and then we can deduce that there exists some constant C > 0 such that
$n \rightarrow \infty$, and then we can deduce that there exists some constant C > 0 such that
 \begin{align}
\int_{D_{u_n}^4} |(f(u_n) - f(u))\varphi|^{\frac{2 N}{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align}
\begin{align}
\int_{D_{u_n}^4} |(f(u_n) - f(u))\varphi|^{\frac{2 N}{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align} provided that ![]() $n \in \mathbb{N}$ is sufficiently large.
$n \in \mathbb{N}$ is sufficiently large.
In addition, from ![]() $u \in {X_\varepsilon}$, it follows that
$u \in {X_\varepsilon}$, it follows that
 \begin{align*}\left|\left\{x \in \mathbb{R}^N : |u(x)| \geqslant L\right\}\right| \rightarrow 0 \ \text{in } \mathbb{R}^N \ \text{as } L \rightarrow +\infty.\end{align*}
\begin{align*}\left|\left\{x \in \mathbb{R}^N : |u(x)| \geqslant L\right\}\right| \rightarrow 0 \ \text{in } \mathbb{R}^N \ \text{as } L \rightarrow +\infty.\end{align*} Using the above fact and invoking (2.25) again, we can infer that there exists ![]() $L :=L(\sigma) \gt 0$ such that
$L :=L(\sigma) \gt 0$ such that
 \begin{align}
&\int_{(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \geqslant L\right\}} |(f(u_n) - f(u))\varphi|^{\frac{2 N}{2 N - \mu}} dx\nonumber\\
\leqslant \ & \int_{(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \geqslant L\right\}} \left|\left(C(\sigma) (|u_n|^{p - 1} + |u|^{p - 1}) + \sigma(|u_n|^{\nu - 1} + |u|^{\nu - 1})\right)\varphi\right|^{\frac{2 N}{2 N - \mu}} dx\nonumber\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C(C (\sigma))^{\frac{2 N}{2 N - \mu}} \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} \left|(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \geqslant L\right\}\right|^{\frac{2 s p - \mu}{p (2 N - \mu)}}\nonumber\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align}
\begin{align}
&\int_{(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \geqslant L\right\}} |(f(u_n) - f(u))\varphi|^{\frac{2 N}{2 N - \mu}} dx\nonumber\\
\leqslant \ & \int_{(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \geqslant L\right\}} \left|\left(C(\sigma) (|u_n|^{p - 1} + |u|^{p - 1}) + \sigma(|u_n|^{\nu - 1} + |u|^{\nu - 1})\right)\varphi\right|^{\frac{2 N}{2 N - \mu}} dx\nonumber\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} + C(C (\sigma))^{\frac{2 N}{2 N - \mu}} \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}} \left|(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \geqslant L\right\}\right|^{\frac{2 s p - \mu}{p (2 N - \mu)}}\nonumber\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}},
\end{align}where C > 0 is a constant. Additionally, we can deduce from the Dominated Convergence Theorem that
 \begin{align*}
\int_{(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \leqslant L\right\}} |f(u_n) - f(u)|^{\frac{2 N p}{(2 N - \mu)(p - 1)}} dx = o_n(1)
\end{align*}
\begin{align*}
\int_{(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \leqslant L\right\}} |f(u_n) - f(u)|^{\frac{2 N p}{(2 N - \mu)(p - 1)}} dx = o_n(1)
\end{align*} for ![]() $n \in \mathbb{N}$ large enough.
$n \in \mathbb{N}$ large enough.
It follows that
 \begin{align}
\int_{(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \leqslant L\right\}} |(f(u_n) - f(u))\varphi|^{\frac{2 N }{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}
\begin{align}
\int_{(B_R \setminus D_{u_n}^4) \cap \left\{x \in \mathbb{R}^N : |u(x)| \leqslant L\right\}} |(f(u_n) - f(u))\varphi|^{\frac{2 N }{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}for some constant C > 0.
Hence, we deduce from (2.32), (2.33), (2.34), and (2.35) that there exists some constant C > 0 such that
 \begin{align}
\int_{B_R} \left|(f(u_n) - f(w_n) - f(u))\varphi\right|^{\frac{2 N}{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align}
\begin{align}
\int_{B_R} \left|(f(u_n) - f(w_n) - f(u))\varphi\right|^{\frac{2 N}{2 N - \mu}} dx \leqslant C \sigma \|\varphi\|_{X_\varepsilon}^{\frac{2 N}{2 N - \mu}}
\end{align} for large enough ![]() $n \in \mathbb{N}$.
$n \in \mathbb{N}$.
Putting together (2.31) and (2.36), we conclude that (2.21) holds true.
On account of the fact that  $\frac{1}{|x|^\mu}*F(u) \in L^\frac{2 N}{\mu}(\mathbb{R}^N)$, for any
$\frac{1}{|x|^\mu}*F(u) \in L^\frac{2 N}{\mu}(\mathbb{R}^N)$, for any ![]() $0 \lt \sigma \lt 1$, there exists
$0 \lt \sigma \lt 1$, there exists ![]() $R_1 :=R_1(\sigma) \gt 0$ such that
$R_1 :=R_1(\sigma) \gt 0$ such that
 \begin{align*}
\left(\int_{\mathbb{R}^N \setminus B_{R_1}} \left|\frac{1}{|x|^\mu}*F(u)\right|^\frac{2 N}{\mu} dx\right)^\frac{\mu}{2 N} \lt \sigma.
\end{align*}
\begin{align*}
\left(\int_{\mathbb{R}^N \setminus B_{R_1}} \left|\frac{1}{|x|^\mu}*F(u)\right|^\frac{2 N}{\mu} dx\right)^\frac{\mu}{2 N} \lt \sigma.
\end{align*} Using the above all information and by a straightforward computation, for ![]() $n \in \mathbb{N}$ large enough, we can conclude that
$n \in \mathbb{N}$ large enough, we can conclude that
 \begin{align}
& \left|\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu}*F(u)\right) f(w_n) \varphi dx\right| \nonumber\\
\leqslant \ & \int_{B_{R_1}} \left|\left(\frac{1}{|x|^\mu}*F(u)\right) f(w_n) \varphi \right| dx + \int_{\mathbb{R}^N \setminus B_{R_1}} \left|\left(\frac{1}{|x|^\mu}*F(u)\right) f(w_n) \varphi \right| dx \nonumber\\
\leqslant \ & C_u \left(\int_{B_{R_1}} |f(w_n) \varphi|^\frac{2 N}{2 N - \mu} dx\right)^{\frac{2 N -\mu}{2 N}}\nonumber\\
+\ & \left(\int_{\mathbb{R}^N \setminus B_{R_1}} \left|\frac{1}{|x|^\mu}*F(u)\right|^\frac{2 N}{\mu} dx\right)^\frac{\mu}{2 N} \left(\int_{\mathbb{R}^N} |f(w_n) \varphi|^{\frac{2 N}{2N - \mu}} dx \right)^\frac{2 N - \mu}{2 N}\nonumber\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon},
\end{align}
\begin{align}
& \left|\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu}*F(u)\right) f(w_n) \varphi dx\right| \nonumber\\
\leqslant \ & \int_{B_{R_1}} \left|\left(\frac{1}{|x|^\mu}*F(u)\right) f(w_n) \varphi \right| dx + \int_{\mathbb{R}^N \setminus B_{R_1}} \left|\left(\frac{1}{|x|^\mu}*F(u)\right) f(w_n) \varphi \right| dx \nonumber\\
\leqslant \ & C_u \left(\int_{B_{R_1}} |f(w_n) \varphi|^\frac{2 N}{2 N - \mu} dx\right)^{\frac{2 N -\mu}{2 N}}\nonumber\\
+\ & \left(\int_{\mathbb{R}^N \setminus B_{R_1}} \left|\frac{1}{|x|^\mu}*F(u)\right|^\frac{2 N}{\mu} dx\right)^\frac{\mu}{2 N} \left(\int_{\mathbb{R}^N} |f(w_n) \varphi|^{\frac{2 N}{2N - \mu}} dx \right)^\frac{2 N - \mu}{2 N}\nonumber\\
\leqslant \ & C \sigma \|\varphi\|_{X_\varepsilon},
\end{align}where Cu and C are positive constants.
Next, we prove the following relation:
 \begin{align}
\left|\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu}*F(w_n)\right) f(u) \varphi dx \right| \leqslant C \sigma\|\varphi\|_{X_\varepsilon}
\end{align}
\begin{align}
\left|\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu}*F(w_n)\right) f(u) \varphi dx \right| \leqslant C \sigma\|\varphi\|_{X_\varepsilon}
\end{align} for ![]() $n \in \mathbb{N}$ sufficiently large.
$n \in \mathbb{N}$ sufficiently large.
Indeed, it is easy to check that, for any ![]() $\sigma \in (0,1)$ and some
$\sigma \in (0,1)$ and some ![]() $R_2 :=R(\sigma) \gt 0$, there exists some constant C > 0 such that
$R_2 :=R(\sigma) \gt 0$, there exists some constant C > 0 such that
 \begin{align}
\int_{B_{R_2}} |F(w_n)| \left(\int_{B_{R_2}} \frac{|f(u(x)) \varphi(x)|}{|x - y|^\mu} dx\right) dy \leqslant C \sigma \|\varphi\|_{X_\varepsilon},
\end{align}
\begin{align}
\int_{B_{R_2}} |F(w_n)| \left(\int_{B_{R_2}} \frac{|f(u(x)) \varphi(x)|}{|x - y|^\mu} dx\right) dy \leqslant C \sigma \|\varphi\|_{X_\varepsilon},
\end{align} \begin{align}
\int_{\mathbb{R}^N} |F(w_n)|\left(\int_{\mathbb{R}^N \setminus B_{R_2}}\frac{|f(u(x)) \varphi(x)|}{|x - y|^\mu} dx \right) dy \leqslant C \sigma \|\varphi\|_{X_\varepsilon}
\end{align}
\begin{align}
\int_{\mathbb{R}^N} |F(w_n)|\left(\int_{\mathbb{R}^N \setminus B_{R_2}}\frac{|f(u(x)) \varphi(x)|}{|x - y|^\mu} dx \right) dy \leqslant C \sigma \|\varphi\|_{X_\varepsilon}
\end{align} for ![]() $n \in \mathbb{N}$ large enough.
$n \in \mathbb{N}$ large enough.
To prove (2.38), now we need to estimate the following part:
 \begin{align*}\Phi_n :=\int_{\mathbb{R}^N \setminus B_{R_2}} |F(w_n)| \left(\int_{B_{R_2}} \frac{|f(u(x)) \varphi(x)|}{|x - y|^\mu} dx\right) dy.\end{align*}
\begin{align*}\Phi_n :=\int_{\mathbb{R}^N \setminus B_{R_2}} |F(w_n)| \left(\int_{B_{R_2}} \frac{|f(u(x)) \varphi(x)|}{|x - y|^\mu} dx\right) dy.\end{align*}To this end, we divide this into two parts for discussion.
(![]() $*$) If
$*$) If ![]() $f(u(x)) \varphi(x) = 0$ a.e. on
$f(u(x)) \varphi(x) = 0$ a.e. on ![]() $B_{R_2}$, so, we have
$B_{R_2}$, so, we have
(![]() $**$) If
$**$) If  $|\left\{x \in B_{R_2} : f(u(x)) \varphi(x) \neq 0\right\}| \gt 0$, that is,
$|\left\{x \in B_{R_2} : f(u(x)) \varphi(x) \neq 0\right\}| \gt 0$, that is,
 \begin{align*}\int_{B_{R_2}} |f(u) \varphi |^{\frac{6N}{6N - \mu}} dx \gt 0.\end{align*}
\begin{align*}\int_{B_{R_2}} |f(u) \varphi |^{\frac{6N}{6N - \mu}} dx \gt 0.\end{align*}In addition, we can easily derive that
 \begin{align*} \int_{B_{R_2}} |f(u)\varphi|^{\frac{6N}{6N - \mu}} dx \leqslant C \|\varphi\|_{X_\varepsilon}^{\frac{6N}{6N - \mu}}|B_{R_2}|^{\frac{2\mu}{6N - \mu}} \ \text{for some constant } C \gt 0.\end{align*}
\begin{align*} \int_{B_{R_2}} |f(u)\varphi|^{\frac{6N}{6N - \mu}} dx \leqslant C \|\varphi\|_{X_\varepsilon}^{\frac{6N}{6N - \mu}}|B_{R_2}|^{\frac{2\mu}{6N - \mu}} \ \text{for some constant } C \gt 0.\end{align*}Let us define
 \begin{align*}
d_\sigma := \left(\frac{|f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})}}{\sigma \|\varphi\|_{X_\varepsilon}}\right)^{\frac{3}{\mu}} \ \text{and }\widehat{R}_2 := R_2 + \sigma^{-\frac{3}{\mu}} |B_{R_2}|^{\frac{6}{6N - \mu}} C^{\frac{6 N - \mu}{2 N\mu}}.
\end{align*}
\begin{align*}
d_\sigma := \left(\frac{|f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})}}{\sigma \|\varphi\|_{X_\varepsilon}}\right)^{\frac{3}{\mu}} \ \text{and }\widehat{R}_2 := R_2 + \sigma^{-\frac{3}{\mu}} |B_{R_2}|^{\frac{6}{6N - \mu}} C^{\frac{6 N - \mu}{2 N\mu}}.
\end{align*} In the case (![]() $**$), we can apply the above relations, theorem 4.3 in the study by Lieb and Loss [Reference Lieb and Loss38], the Sobolev continuous embedding and the local compactness Sobolev embedding to infer that, for
$**$), we can apply the above relations, theorem 4.3 in the study by Lieb and Loss [Reference Lieb and Loss38], the Sobolev continuous embedding and the local compactness Sobolev embedding to infer that, for ![]() $n \in \mathbb{N}$ sufficiently large,
$n \in \mathbb{N}$ sufficiently large,
 \begin{align}
\Phi_n & = \int_{B_{R_2}} |f(u) \varphi| \left(\int_{\mathbb{R}^N \setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& =\int_{B_{R_2}} |f(u) \varphi| \left(\int_{\mathbb{R}^N \setminus B_{R_2 + d_\sigma}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{R_2 + d_\sigma}} \setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C \frac{\sigma\|\varphi\|_{X_\varepsilon}}{|f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})}}\int_{B_{R_2}} |f(u)\varphi| \left(\int_{\mathbb{R}^N \setminus B_{R_2 + d_\sigma}} \frac{|F(w_n(y))|}{|x - y|^{2\mu / 3}} dy\right) dx\nonumber\\
& + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{R_2 + d_\sigma}} \setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C \frac{\sigma\|\varphi\|_{X_\varepsilon}}{|f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})}}\int_{B_{R_2}} |f(u)\varphi| \left(\int_{\mathbb{R}^N} \frac{|F(w_n(y))|}{|x - y|^{2\mu / 3}} dy\right) dx\nonumber\\
& + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{R_2 + d_\sigma}} \setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C \frac{\sigma\|\varphi\|_{X_\varepsilon}}{|f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})}} |f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})} \nonumber\\
& + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{\widehat{R}_2}}\setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C\sigma \|\varphi\|_{X_\varepsilon} + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{\widehat{R}_2}}\setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C \sigma\|\varphi\|_{X_\varepsilon}.
\end{align}
\begin{align}
\Phi_n & = \int_{B_{R_2}} |f(u) \varphi| \left(\int_{\mathbb{R}^N \setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& =\int_{B_{R_2}} |f(u) \varphi| \left(\int_{\mathbb{R}^N \setminus B_{R_2 + d_\sigma}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{R_2 + d_\sigma}} \setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C \frac{\sigma\|\varphi\|_{X_\varepsilon}}{|f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})}}\int_{B_{R_2}} |f(u)\varphi| \left(\int_{\mathbb{R}^N \setminus B_{R_2 + d_\sigma}} \frac{|F(w_n(y))|}{|x - y|^{2\mu / 3}} dy\right) dx\nonumber\\
& + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{R_2 + d_\sigma}} \setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C \frac{\sigma\|\varphi\|_{X_\varepsilon}}{|f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})}}\int_{B_{R_2}} |f(u)\varphi| \left(\int_{\mathbb{R}^N} \frac{|F(w_n(y))|}{|x - y|^{2\mu / 3}} dy\right) dx\nonumber\\
& + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{R_2 + d_\sigma}} \setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C \frac{\sigma\|\varphi\|_{X_\varepsilon}}{|f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})}} |f(u)\varphi|_{L^{\frac{6N}{6N - \mu}}(B_{R_2})} \nonumber\\
& + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{\widehat{R}_2}}\setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C\sigma \|\varphi\|_{X_\varepsilon} + \int_{B_{R_2}} |f(u) \varphi| \left(\int_{ {B_{\widehat{R}_2}}\setminus B_{R_2}} \frac{|F(w_n(y))|}{|x - y|^\mu} dy\right) dx\nonumber\\
& \leqslant C \sigma\|\varphi\|_{X_\varepsilon}.
\end{align} Thus, relations (2.39), (2.41), and (2.42) and (![]() $*$) imply that (2.38) holds true.
$*$) imply that (2.38) holds true.
Finally, we point out that
 \begin{align*}
& \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) f(u_n) \varphi dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) f(w_n) \varphi dx\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * \left(F(u_n) - F(w_n)\right)\right) (f(u_n) - f(w_n))\varphi dx\\
+ \ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * (F(u_n) - F(w_n))\right) f(w_n) \varphi dx \\
+ \ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) (f(u_n) - f(w_n)) \varphi dx.
\end{align*}
\begin{align*}
& \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) f(u_n) \varphi dx - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) f(w_n) \varphi dx\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * \left(F(u_n) - F(w_n)\right)\right) (f(u_n) - f(w_n))\varphi dx\\
+ \ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * (F(u_n) - F(w_n))\right) f(w_n) \varphi dx \\
+ \ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(w_n)\right) (f(u_n) - f(w_n)) \varphi dx.
\end{align*} Then, the above equality combined with (2.19), (2.20), (2.21), (2.37), and (2.38); theorem 4.3 in the study by Lieb and Loss [Reference Lieb and Loss38]; the Hölder inequality; the boundedness of the sequence ![]() $\left\{u_n\right\}_{n \in\mathbb{N}} \subset {X_\varepsilon}$; and the fact that
$\left\{u_n\right\}_{n \in\mathbb{N}} \subset {X_\varepsilon}$; and the fact that ![]() $\|\varphi\|_{X_\varepsilon} \leqslant 1$ yields that (f) is true. This proof is now complete.
$\|\varphi\|_{X_\varepsilon} \leqslant 1$ yields that (f) is true. This proof is now complete.
3. The limit problem
To the best of our knowledge, there is no result about the nonlinear fractional (p, q)-Choquard problem. That is why we need to consider the following limit problem associated with problem (1.3):
 \begin{align}
\left\{
\begin{array}{lll}
(- \Delta)_p^s u + (- \Delta)_q ^s u + V_0 (|u|^{p - 2} u + |u|^{q - 2} u) = \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N, \\
u \in W^{s,p}(\mathbb{R}^N) \cap W^{s,q}(\mathbb{R}^N) ,\ u \gt 0 & \ \text{in } \mathbb{R}^N.
\end{array}
\right\}
\end{align}
\begin{align}
\left\{
\begin{array}{lll}
(- \Delta)_p^s u + (- \Delta)_q ^s u + V_0 (|u|^{p - 2} u + |u|^{q - 2} u) = \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) & \ \text{in }\mathbb{R}^N, \\
u \in W^{s,p}(\mathbb{R}^N) \cap W^{s,q}(\mathbb{R}^N) ,\ u \gt 0 & \ \text{in } \mathbb{R}^N.
\end{array}
\right\}
\end{align} It is worth pointing out that we denote by ![]() $X_{V_0}$ the space Xɛ when ɛ = 0. For all
$X_{V_0}$ the space Xɛ when ɛ = 0. For all ![]() $u \in {X_{V_0}}$, we introduce the corresponding energy functional associated with problem (3.1) defined by
$u \in {X_{V_0}}$, we introduce the corresponding energy functional associated with problem (3.1) defined by
 \begin{align*}I_{V_0}(u) := \frac{1}{p} [u]_{s,p}^p + \frac{1}{q} [u]_{s,q}^q + V_0 \left(\frac{1}{p} |u|_p^p +\frac{1}{q} |u|_q^q\right) - \frac{1}{2} \int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * F(u)\right) F(u) dx.\end{align*}
\begin{align*}I_{V_0}(u) := \frac{1}{p} [u]_{s,p}^p + \frac{1}{q} [u]_{s,q}^q + V_0 \left(\frac{1}{p} |u|_p^p +\frac{1}{q} |u|_q^q\right) - \frac{1}{2} \int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * F(u)\right) F(u) dx.\end{align*} It is obvious that the functional ![]() $I_{V_0}$ is well-defined and belongs to C 1, with its differential given by
$I_{V_0}$ is well-defined and belongs to C 1, with its differential given by
 \begin{align*}
\langle I_{V_0}'(u),v \rangle & = \langle u ,v \rangle_{s,p} + \langle u, v \rangle_{s,q} + \int_{\mathbb{R}^N} V_0 \left(|u|^{p - 2} u + |u|^{q - 2} u \right) v dx \\
& - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) v dx,
\end{align*}
\begin{align*}
\langle I_{V_0}'(u),v \rangle & = \langle u ,v \rangle_{s,p} + \langle u, v \rangle_{s,q} + \int_{\mathbb{R}^N} V_0 \left(|u|^{p - 2} u + |u|^{q - 2} u \right) v dx \\
& - \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u)\right) f(u) v dx,
\end{align*} for all u, ![]() $v \in {X_{V_0}}$. So, it is easy to check that all the solutions of problem (3.1) correspond to critical points of the functional
$v \in {X_{V_0}}$. So, it is easy to check that all the solutions of problem (3.1) correspond to critical points of the functional ![]() $I_{V_0}$.
$I_{V_0}$.
Next, we denote by ![]() $\mathcal{M}_{V_0}$ the Nehari manifold associated with the functional
$\mathcal{M}_{V_0}$ the Nehari manifold associated with the functional ![]() $I_{V_0}$, that is,
$I_{V_0}$, that is,
 \begin{align*}\mathcal{M}_{V_0} := \left\{u \in {X_{V_0}} \setminus \{0\} : \langle I_{V_0}'(u),u \rangle = 0\right\}.\end{align*}
\begin{align*}\mathcal{M}_{V_0} := \left\{u \in {X_{V_0}} \setminus \{0\} : \langle I_{V_0}'(u),u \rangle = 0\right\}.\end{align*} Moreover, we define  $c_{V_0} : =\inf_{u \in \mathcal{M}_{V_0}} I_{V_0}(u)$.
$c_{V_0} : =\inf_{u \in \mathcal{M}_{V_0}} I_{V_0}(u)$.
Now, we define the following sets:
 \begin{align*}X_{V_0}^+ := \left\{u \in X_{V_0} : |{\mathrm{supp}\,} (u^+)| \gt 0\right\} \quad \ \text{and } \quad S_{V_0}^+ = S_{V_0} \cap {X_{V_0}^+},\end{align*}
\begin{align*}X_{V_0}^+ := \left\{u \in X_{V_0} : |{\mathrm{supp}\,} (u^+)| \gt 0\right\} \quad \ \text{and } \quad S_{V_0}^+ = S_{V_0} \cap {X_{V_0}^+},\end{align*} where ![]() $S_{V_0}$ is the unit sphere of
$S_{V_0}$ is the unit sphere of ![]() $X_{V_0}$. We point out that
$X_{V_0}$. We point out that  $S_{V_0}^+$ is also an incomplete
$S_{V_0}^+$ is also an incomplete ![]() $C^{1,1}$-manifold of codimension one and contained in
$C^{1,1}$-manifold of codimension one and contained in  $X_{V_0}^+$. Hence,
$X_{V_0}^+$. Hence,  $X_{V_0} = T_u (S_{V_0}^+)\bigoplus \mathbb{R} u$ for each
$X_{V_0} = T_u (S_{V_0}^+)\bigoplus \mathbb{R} u$ for each  $u \in S_{V_0}^+$, where
$u \in S_{V_0}^+$, where
 \begin{align*}
T_u (S_{V_0}^+) := \left\{v \in {X_{V_0}} : \langle u, v \rangle_{s,p} + \langle u, v \rangle_{s,q} + \int_{\mathbb{R}^N} V_0\left(|u|^{p - 2} u + |u|^{q - 2} u \right) vdx= 0 \right\}.
\end{align*}
\begin{align*}
T_u (S_{V_0}^+) := \left\{v \in {X_{V_0}} : \langle u, v \rangle_{s,p} + \langle u, v \rangle_{s,q} + \int_{\mathbb{R}^N} V_0\left(|u|^{p - 2} u + |u|^{q - 2} u \right) vdx= 0 \right\}.
\end{align*}With arguments as in the proof of lemma 2.2, we can deduce that the following property holds true.
Lemma 3.1. Assume that ![]() $(f_1)$–
$(f_1)$–![]() $(f_4)$ and
$(f_4)$ and ![]() $(V_1)$ are fulfilled, then we have the following properties:
$(V_1)$ are fulfilled, then we have the following properties:
(a) for all
 $u \in {X_{V_0}^+}$, there exists a unique
$u \in {X_{V_0}^+}$, there exists a unique  $t_u \gt 0$ such that
$t_u \gt 0$ such that  $t_u u \in \mathcal{M}_{V_0}.$ Furthermore,
$t_u u \in \mathcal{M}_{V_0}.$ Furthermore,  $\hat{m}_{V_0}(u) = t_u u$ is the unique maximum of
$\hat{m}_{V_0}(u) = t_u u$ is the unique maximum of  $I_{V_0}(t u);$
$I_{V_0}(t u);$(b) there exists τ > 0 independent of u such that
 $t_u \geqslant \tau$ for all
$t_u \geqslant \tau$ for all  $u \in S_{V_0}^+.$ Moreover, for each compact set
$u \in S_{V_0}^+.$ Moreover, for each compact set  $\mathcal{W} \subset S_{V_0}^+,$ there exists a constant
$\mathcal{W} \subset S_{V_0}^+,$ there exists a constant  $C_\mathcal{W} \gt 0$ such that
$C_\mathcal{W} \gt 0$ such that  $t_u \leqslant C_\mathcal{W}$ for all
$t_u \leqslant C_\mathcal{W}$ for all  $u \in \mathcal{W};$
$u \in \mathcal{W};$(c) the mapping
 $\hat{m}_{V_0} : {X_{V_0}^+} \mapsto \mathcal{M}_{V_0}$ is continuous,
$\hat{m}_{V_0} : {X_{V_0}^+} \mapsto \mathcal{M}_{V_0}$ is continuous,  $m_{V_0} :=\hat{m}_{V_0} |_{S_{V_0}^+}$ is a homeomorphism between
$m_{V_0} :=\hat{m}_{V_0} |_{S_{V_0}^+}$ is a homeomorphism between  $S_{V_0}^+$ and
$S_{V_0}^+$ and  $\mathcal{M}_{V_0},$ and the inverse of
$\mathcal{M}_{V_0},$ and the inverse of  $m_{V_0}$ is given by
$m_{V_0}$ is given by  $m_{V_0}^{-1}(u) := u / \|u\|_{X_{V_0}};$
$m_{V_0}^{-1}(u) := u / \|u\|_{X_{V_0}};$(d)
 $c_{V_0} : = \inf_{u \in \mathcal{M}_{V_0}} I_{V_0}(u) \gt 0$, and
$c_{V_0} : = \inf_{u \in \mathcal{M}_{V_0}} I_{V_0}(u) \gt 0$, and  $I_{V_0}$ is bounded below on
$I_{V_0}$ is bounded below on  $\mathcal{M}_{V_0}$ by some positive constant
$\mathcal{M}_{V_0}$ by some positive constant $;$
$;$(e) let
 $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and  $\nu \lt (N - \mu) q / (N - sq).$ If there exists a sequence
$\nu \lt (N - \mu) q / (N - sq).$ If there exists a sequence  $\left\{u_n\right\}_{n \in \mathbb{N}} \subset S_{V_0}^+$ such that
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset S_{V_0}^+$ such that  ${\mathrm{dist}\,}(u_n,\partial S_\varepsilon^+) \rightarrow 0$ as
${\mathrm{dist}\,}(u_n,\partial S_\varepsilon^+) \rightarrow 0$ as  $n \rightarrow \infty,$ then
$n \rightarrow \infty,$ then  $\|m_{V_0}(u_n)\|_{X_{V_0}} \rightarrow + \infty$ and
$\|m_{V_0}(u_n)\|_{X_{V_0}} \rightarrow + \infty$ and  $J_\varepsilon(m_\varepsilon(u_n)) \rightarrow + \infty$ as
$J_\varepsilon(m_\varepsilon(u_n)) \rightarrow + \infty$ as  $n \rightarrow \infty;$
$n \rightarrow \infty;$(f)
 $I_{V_0}$ is coercive on
$I_{V_0}$ is coercive on  $\mathcal{M}_{V_0}.$
$\mathcal{M}_{V_0}.$
Now, let us define the mappings
 \begin{align*}\hat{\psi}_{V_0} : {X_{V_0}^+} \mapsto \mathbb{R} \quad \ \text{and } \quad \psi_{V_0} : S_{V_0}^+ \mapsto \mathbb{R}\end{align*}
\begin{align*}\hat{\psi}_{V_0} : {X_{V_0}^+} \mapsto \mathbb{R} \quad \ \text{and } \quad \psi_{V_0} : S_{V_0}^+ \mapsto \mathbb{R}\end{align*} by  $\hat{\psi}_{V_0}(u) := I_{V_0}(\hat{m}_{V_0}(u))$ for all
$\hat{\psi}_{V_0}(u) := I_{V_0}(\hat{m}_{V_0}(u))$ for all  $u \in {X_{V_0}^+}$ and
$u \in {X_{V_0}^+}$ and  $\psi_{V_0} := \hat{\psi}_{V_0} |_{S_{V_0}^+}$.
$\psi_{V_0} := \hat{\psi}_{V_0} |_{S_{V_0}^+}$.
Lemma 3.2. Assume that ![]() $(f_1)$–
$(f_1)$–![]() $(f_4)$ and
$(f_4)$ and ![]() $(V_1)$ hold true. Then,
$(V_1)$ hold true. Then,
(a)
 $\hat{\psi}_{V_0} \in C^1({X_{V_0}^+},\mathbb{R})$ and
$\hat{\psi}_{V_0} \in C^1({X_{V_0}^+},\mathbb{R})$ and  $\langle \hat{\psi}'_{V_0}(u), v\rangle = \frac{\|\hat{m}_{V_0}(u)\|_{X_{V_0}}}{\|u\|_{X_{V_0}}} \langle I_{V_0}'(\hat{m}_{V_0}(u)),v\rangle$ for all
$\langle \hat{\psi}'_{V_0}(u), v\rangle = \frac{\|\hat{m}_{V_0}(u)\|_{X_{V_0}}}{\|u\|_{X_{V_0}}} \langle I_{V_0}'(\hat{m}_{V_0}(u)),v\rangle$ for all  $u \in {X_{V_0}^+},$ all
$u \in {X_{V_0}^+},$ all  $v \in {X_{V_0}};$
$v \in {X_{V_0}};$(b)
 $\psi_{V_0} \in C^1(S_{V_0}^+,\mathbb{R})$ and
$\psi_{V_0} \in C^1(S_{V_0}^+,\mathbb{R})$ and  $\langle \psi'_{V_0}(u),v\rangle = \|m_{V_0}(u)\|_{X_{V_0}} \langle I_{V_0}'(m_{V_0}(u)),v\rangle$ for all
$\langle \psi'_{V_0}(u),v\rangle = \|m_{V_0}(u)\|_{X_{V_0}} \langle I_{V_0}'(m_{V_0}(u)),v\rangle$ for all  $u \in S_{V_0}^+,$ all
$u \in S_{V_0}^+,$ all  $v \in T_u(S_{V_0}^+);$
$v \in T_u(S_{V_0}^+);$(c) if
 $\{u_n\}_{n \in \mathbb{N}}$ is a Palais–Smale sequence for
$\{u_n\}_{n \in \mathbb{N}}$ is a Palais–Smale sequence for  $\psi_{V_0},$ then
$\psi_{V_0},$ then  $\{m_{V_0}(u_n)\}_{n \in \mathbb{N}}$ is a Palais–Smale sequence for
$\{m_{V_0}(u_n)\}_{n \in \mathbb{N}}$ is a Palais–Smale sequence for  $I_{V_0}.$ If
$I_{V_0}.$ If  $\{u_n\}_{n \in \mathbb{N}} \subset \mathcal{M}_{V_0}$ is a bounded Palais–Smale sequence for
$\{u_n\}_{n \in \mathbb{N}} \subset \mathcal{M}_{V_0}$ is a bounded Palais–Smale sequence for  $I_{V_0},$ then
$I_{V_0},$ then  $\{m_{V_0}^{- 1}(u_n)\}_{n \in \mathbb{N}} \subset S_{V_0}^+$ is a Palais–Smale sequence for
$\{m_{V_0}^{- 1}(u_n)\}_{n \in \mathbb{N}} \subset S_{V_0}^+$ is a Palais–Smale sequence for  $\psi_{V_0};$
$\psi_{V_0};$(d)
 $u \in S_{V_0}^+$ is a critical point of
$u \in S_{V_0}^+$ is a critical point of  $\psi_{V_0}$ if and only if
$\psi_{V_0}$ if and only if  $m_{V_0}(u) \in \mathcal{M}_{V_0}$ is a critical point of
$m_{V_0}(u) \in \mathcal{M}_{V_0}$ is a critical point of  $I_{V_0}.$ Moreover, the corresponding critical values coincide and
$I_{V_0}.$ Moreover, the corresponding critical values coincide and
 \begin{align*}\inf_{u \in S_{V_0}^+} \psi_{V_0}(u) = \inf_{u \in \mathcal{M}_{V_0}}I_{V_0}(u) = c_{V_0}.\end{align*}
\begin{align*}\inf_{u \in S_{V_0}^+} \psi_{V_0}(u) = \inf_{u \in \mathcal{M}_{V_0}}I_{V_0}(u) = c_{V_0}.\end{align*}
Remark 3.3. The following variational characterization for ![]() $c_{V_0}$ is fulfilled:
$c_{V_0}$ is fulfilled:
 \begin{align*}c_{V_0} = \inf_{u \in \mathcal{M}_{V_0}} I_{V_0}(u) = \inf_{u \in {X_{V_0}^+}} \max_{t \gt 0} I_{V_0}(t u) = \inf_{u \in S_{V_0}^+} \max_{t \gt 0} I_{V_0}(t u).\end{align*}
\begin{align*}c_{V_0} = \inf_{u \in \mathcal{M}_{V_0}} I_{V_0}(u) = \inf_{u \in {X_{V_0}^+}} \max_{t \gt 0} I_{V_0}(t u) = \inf_{u \in S_{V_0}^+} \max_{t \gt 0} I_{V_0}(t u).\end{align*}Lemma 3.4. Assume that ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is a Palais–Smale sequence of the functional
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is a Palais–Smale sequence of the functional ![]() $I_{V_0}$ at the level
$I_{V_0}$ at the level ![]() $c_{V_0}.$ Then, the sequence
$c_{V_0}.$ Then, the sequence ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is bounded, and there exist a sequence
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is bounded, and there exist a sequence  $\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ and some constants
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ and some constants ![]() $R,$ α > 0 such that
$R,$ α > 0 such that
 \begin{align*}\liminf_{n \rightarrow \infty} \int_{B_R(y_n)} |u_n|^q dx \geqslant \alpha.\end{align*}
\begin{align*}\liminf_{n \rightarrow \infty} \int_{B_R(y_n)} |u_n|^q dx \geqslant \alpha.\end{align*}Proof. Arguing as in lemma 2.5, it is obvious to see that ![]() $\left\{u_n\right\}_{n \in
\mathbb{N}} \subset {X_{V_0}}$ is bounded. Now, arguing by contradiction, suppose that for any R > 0, the following relation
$\left\{u_n\right\}_{n \in
\mathbb{N}} \subset {X_{V_0}}$ is bounded. Now, arguing by contradiction, suppose that for any R > 0, the following relation
 \begin{align*}\lim_{n \rightarrow \infty}\sup_{y \in \mathbb{R}^N} \int_{B_R(y)} |u_n|^q dx = 0\end{align*}
\begin{align*}\lim_{n \rightarrow \infty}\sup_{y \in \mathbb{R}^N} \int_{B_R(y)} |u_n|^q dx = 0\end{align*} holds true. Then, using lemma 2.2 in the study by Alves, Ambrosio, and Isernia [Reference Alves, Ambrosio and Isernia1], we know that for all ![]() $r \in (p,q_s^*)$,
$r \in (p,q_s^*)$,
So, we deduce from theorem 4.3 in the study by Lieb and Loss [Reference Lieb and Loss38], hypotheses ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, the boundedness of the sequence
$(f_2)$, the boundedness of the sequence ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$, and (3.2) that
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$, and (3.2) that
 \begin{align*}\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) f(u_n) u_n dx = 0.\end{align*}
\begin{align*}\lim_{n \rightarrow \infty}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) f(u_n) u_n dx = 0.\end{align*} Moreover, by the boundedness of the sequence ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$, we see that
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$, we see that  $\langle I_{V_0}'(u_n),u_n \rangle = o_n(1)$ as
$\langle I_{V_0}'(u_n),u_n \rangle = o_n(1)$ as ![]() $n \rightarrow \infty$, that is,
$n \rightarrow \infty$, that is,
 \begin{align*}& \quad [u_n]_{s,p}^p + [u_n]_{s,q}^q + V_0 \left(|u_n|_p^p + |u_n|_q^q \right) \\
& = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) f(u_n) u_n dx + o_n(1) \ \text{as } n \rightarrow \infty.\end{align*}
\begin{align*}& \quad [u_n]_{s,p}^p + [u_n]_{s,q}^q + V_0 \left(|u_n|_p^p + |u_n|_q^q \right) \\
& = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(u_n)\right) f(u_n) u_n dx + o_n(1) \ \text{as } n \rightarrow \infty.\end{align*} This implies that  $\|u_n\|_{X_{V_0}} = o_n(1)$ as
$\|u_n\|_{X_{V_0}} = o_n(1)$ as ![]() $n \rightarrow \infty$. We get a contradiction since
$n \rightarrow \infty$. We get a contradiction since ![]() $I_{V_0}(u_n) \rightarrow c_{V_0} \gt 0$ in
$I_{V_0}(u_n) \rightarrow c_{V_0} \gt 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$. The proof is now complete.
$n \rightarrow \infty$. The proof is now complete.
Theorem 3.5 Problem (3.1) has a positive ground state solution.
Proof. We deduce from a variant of the Mountain Pass Theorem without the Palais–Smale condition that there is a Palais–Smale sequence ![]() $\left\{u_n\right\}_{n\in \mathbb{N}} \subset {X_{V_0}}$ of the functional
$\left\{u_n\right\}_{n\in \mathbb{N}} \subset {X_{V_0}}$ of the functional ![]() $I_{V_0}$ at the level
$I_{V_0}$ at the level ![]() $c_{V_0}$. As in the proof of lemma 2.5, we can conclude that the sequence
$c_{V_0}$. As in the proof of lemma 2.5, we can conclude that the sequence ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is bounded. Then, we are able to deduce from lemma 3.4 that there exist a sequence
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is bounded. Then, we are able to deduce from lemma 3.4 that there exist a sequence  $\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ and some constants R, α > 0
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ and some constants R, α > 0
 \begin{align*}\liminf_{n \rightarrow \infty} \int_{B_R(y_n)} |u_n|^q dx \geqslant \alpha.\end{align*}
\begin{align*}\liminf_{n \rightarrow \infty} \int_{B_R(y_n)} |u_n|^q dx \geqslant \alpha.\end{align*} Set ![]() $v_n(x) : = u_n(x + y_n)$. Then, we have
$v_n(x) : = u_n(x + y_n)$. Then, we have
 \begin{align*}\int_{B_R(0)} |v_n|^q dx \geqslant \frac{\alpha}{2}.\end{align*}
\begin{align*}\int_{B_R(0)} |v_n|^q dx \geqslant \frac{\alpha}{2}.\end{align*} It is easy to check that ![]() $I_{V_0}(v_n) \rightarrow c_{V_0}$ in
$I_{V_0}(v_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ and
$\mathbb{R}$ and  $I_{V_0}'(v_n) \rightarrow 0$ in
$I_{V_0}'(v_n) \rightarrow 0$ in ![]() ${X_{V_0}}^*$ as
${X_{V_0}}^*$ as ![]() $n \rightarrow \infty$. Clearly, the sequence
$n \rightarrow \infty$. Clearly, the sequence ![]() $\left\{v_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is also bounded. Thus, we may suppose that there exists
$\left\{v_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is also bounded. Thus, we may suppose that there exists ![]() $0 \neq v \in {X_{V_0}}$ such that
$0 \neq v \in {X_{V_0}}$ such that ![]() $v_n \xrightarrow w v$ (up to a subsequence) in
$v_n \xrightarrow w v$ (up to a subsequence) in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$. Moreover, arguing as in lemma 2.7, we have
$n \rightarrow \infty$. Moreover, arguing as in lemma 2.7, we have  $I_{V_0}'(v) = 0$. Due to v ≠ 0, we can derive that
$I_{V_0}'(v) = 0$. Due to v ≠ 0, we can derive that ![]() $v \in \mathcal{M}_{V_0}$, and so
$v \in \mathcal{M}_{V_0}$, and so ![]() $I_{V_0}(v) \geqslant c_{V_0}$. On the other hand, from hypothesis
$I_{V_0}(v) \geqslant c_{V_0}$. On the other hand, from hypothesis ![]() $(f_3)$ and Fatou’s Lemma, we deduce that
$(f_3)$ and Fatou’s Lemma, we deduce that
 \begin{align*}I_{V_0}(v) = I_{V_0}(v) - \frac{1}{q}\langle I_{V_0}'(v),v\rangle \leqslant \liminf_{n \rightarrow \infty} \left(I_{V_0}(v_n) - \frac{1}{q} \langle I_{V_0}'(v_n),v_n\rangle\right) = c_{V_0}.\end{align*}
\begin{align*}I_{V_0}(v) = I_{V_0}(v) - \frac{1}{q}\langle I_{V_0}'(v),v\rangle \leqslant \liminf_{n \rightarrow \infty} \left(I_{V_0}(v_n) - \frac{1}{q} \langle I_{V_0}'(v_n),v_n\rangle\right) = c_{V_0}.\end{align*} So, we obtain ![]() $I_{V_0}(v) = c_{V_0}$.
$I_{V_0}(v) = c_{V_0}$.
We can also show that this ground state solution v is positive. Set ![]() $v^- :=\min\left\{v,0\right\}$, and then
$v^- :=\min\left\{v,0\right\}$, and then ![]() $v^- \in {X_{V_0}}$. Recalling that
$v^- \in {X_{V_0}}$. Recalling that ![]() $f(t) = 0$ for
$f(t) = 0$ for ![]() $t \leqslant 0$ and using
$t \leqslant 0$ and using  $\langle I_{V_0}'(v),v^- \rangle = 0$, we obtain
$\langle I_{V_0}'(v),v^- \rangle = 0$, we obtain
 \begin{align*}\|v^-\|_{V_0,p}^p + \|v^-\|_{V_0,q}^q \leqslant 0.\end{align*}
\begin{align*}\|v^-\|_{V_0,p}^p + \|v^-\|_{V_0,q}^q \leqslant 0.\end{align*} This leads to ![]() $v^- = 0$, and so
$v^- = 0$, and so ![]() $v \geqslant 0$ on
$v \geqslant 0$ on ![]() $\mathbb{R}^N$. Thus,
$\mathbb{R}^N$. Thus, ![]() $v \geqslant 0$ and
$v \geqslant 0$ and ![]() $v \not \equiv 0$. Similar to the proof of lemma 6.1, we see that
$v \not \equiv 0$. Similar to the proof of lemma 6.1, we see that ![]() $v \in L^\infty(\mathbb{R}^N)$. In addition, from corollary 2.1 in the study by Ambrosio and Rădulescu [Reference Ambrosio and Rădulescu11], it follows that
$v \in L^\infty(\mathbb{R}^N)$. In addition, from corollary 2.1 in the study by Ambrosio and Rădulescu [Reference Ambrosio and Rădulescu11], it follows that ![]() $v \in C^\sigma(\mathbb{R}^N)$ for some
$v \in C^\sigma(\mathbb{R}^N)$ for some ![]() $\sigma \in (0,1)$. Now, it follows from the proof of theorem 1.1 (ii) in the study by Jarohs [Reference Jarohs33] that v > 0 on
$\sigma \in (0,1)$. Now, it follows from the proof of theorem 1.1 (ii) in the study by Jarohs [Reference Jarohs33] that v > 0 on ![]() $\mathbb{R}^N$. This ends the proof.
$\mathbb{R}^N$. This ends the proof.
Next, we introduce a compactness result for the autonomous problem, which will be very useful in the sequel.
Lemma 3.6. Let ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq).$ Assume that
$\nu \lt (N - \mu) q / (N - sq).$ Assume that ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset \mathcal{M}_{V_0}$ is a sequence satisfying
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset \mathcal{M}_{V_0}$ is a sequence satisfying ![]() $I_{V_0}(u_n) \rightarrow c_{V_0}$ in
$I_{V_0}(u_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty,$ then the sequence
$n \rightarrow \infty,$ then the sequence ![]() $\left\{u_n(\cdot + y_n)\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ possesses a convergent subsequence for some sequence
$\left\{u_n(\cdot + y_n)\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ possesses a convergent subsequence for some sequence  $\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N.$
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N.$
Proof. On account of the fact that ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset \mathcal{M}_{V_0}$ and
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset \mathcal{M}_{V_0}$ and ![]() $I_{V_0}(u_n) \rightarrow c_{V_0}$ in
$I_{V_0}(u_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$, lemma 3.1 (c), lemma 3.2 (d), and the definition of
$n \rightarrow \infty$, lemma 3.1 (c), lemma 3.2 (d), and the definition of ![]() $c_{V_0}$ imply that
$c_{V_0}$ imply that
 \begin{align*}w_n := m_{V_0}^{-1}(u_n) \in S_{V_0}^+ \ \text{for all } n \in \mathbb{N}\end{align*}
\begin{align*}w_n := m_{V_0}^{-1}(u_n) \in S_{V_0}^+ \ \text{for all } n \in \mathbb{N}\end{align*}and
 \begin{align*}\psi_{V_0}(w_n) = I_{V_0}(u_n) \rightarrow c_{V_0} = \inf_{w \in S_{V_0}^+} \psi_{V_0}(w) \ \text{in } \mathbb{R} \ \text{as } n \rightarrow \infty.\end{align*}
\begin{align*}\psi_{V_0}(w_n) = I_{V_0}(u_n) \rightarrow c_{V_0} = \inf_{w \in S_{V_0}^+} \psi_{V_0}(w) \ \text{in } \mathbb{R} \ \text{as } n \rightarrow \infty.\end{align*}Now, we introduce the following map:
 \begin{align*}
\mathcal{I}(u) =
\begin{cases}
\ \psi_{V_0}(u) \quad & \ \text{if } u \in S_{V_0}^+,\\
\ + \infty\quad & \ \text{if } u \in \partial S_{V_0}^+.
\end{cases}
\end{align*}
\begin{align*}
\mathcal{I}(u) =
\begin{cases}
\ \psi_{V_0}(u) \quad & \ \text{if } u \in S_{V_0}^+,\\
\ + \infty\quad & \ \text{if } u \in \partial S_{V_0}^+.
\end{cases}
\end{align*}It is worth pointing out the following essential facts:
(i)
 $(\overline{S_{V_0}^+}, \delta_{V_0})$, where
$(\overline{S_{V_0}^+}, \delta_{V_0})$, where  $\delta_{V_0}(u,v) = \|u - v\|_{X_{V_0}}$, is a complete metric space;
$\delta_{V_0}(u,v) = \|u - v\|_{X_{V_0}}$, is a complete metric space;(ii)
 $\mathcal{I} \in C(\overline{S_{V_0}^+},\mathbb{R} \cup \left\{+ \infty\right\})$, by lemma 3.1 (e);
$\mathcal{I} \in C(\overline{S_{V_0}^+},\mathbb{R} \cup \left\{+ \infty\right\})$, by lemma 3.1 (e);(iii)
 $\mathcal{I}$ is bounded below, by lemma 3.2 (d).
$\mathcal{I}$ is bounded below, by lemma 3.2 (d).
We deduce from the Ekeland variational principle (see the study by Ekeland [Reference Ekeland28]) that there exists a Palais–Smale sequence  $\left\{\hat{w}_n\right\}_{n \in \mathbb{N}} \subset S_{V_0}^+$ of the functional
$\left\{\hat{w}_n\right\}_{n \in \mathbb{N}} \subset S_{V_0}^+$ of the functional ![]() $\psi_{V_0}$ at the level
$\psi_{V_0}$ at the level ![]() $c_{V_0}$ such that
$c_{V_0}$ such that  $\|\hat{w}_n - w_n\|_{X_{V_0}} = o_n(1)$ as
$\|\hat{w}_n - w_n\|_{X_{V_0}} = o_n(1)$ as ![]() $n \rightarrow \infty$, that is,
$n \rightarrow \infty$, that is, ![]() $\psi_{V_0}(\hat{w}_n) \rightarrow c_{V_0}$ in
$\psi_{V_0}(\hat{w}_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ and
$\mathbb{R}$ and  $\psi_{V_0}'(\hat{w}_n) \rightarrow 0$ in
$\psi_{V_0}'(\hat{w}_n) \rightarrow 0$ in  ${T_{\hat{w}_n}(S_{V_0}^+)}^*$ as
${T_{\hat{w}_n}(S_{V_0}^+)}^*$ as ![]() $n \rightarrow \infty$. Therefore, from lemma 3.2 (c), it follows that the sequence
$n \rightarrow \infty$. Therefore, from lemma 3.2 (c), it follows that the sequence  $\left\{m_{V_0}(\hat{w}_n)\right\}_{n \in \mathbb{N}} \subset \mathcal{M}_{V_0}$ is the Palais–Smale sequence of the functional
$\left\{m_{V_0}(\hat{w}_n)\right\}_{n \in \mathbb{N}} \subset \mathcal{M}_{V_0}$ is the Palais–Smale sequence of the functional ![]() $I_{V_0}$ at the level
$I_{V_0}$ at the level ![]() $c_{V_0}$. Then, we can conclude that the sequence
$c_{V_0}$. Then, we can conclude that the sequence  $\left\{m_{V_0}(\hat{w}_n)\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is the bounded Palais–Smale sequence at the level
$\left\{m_{V_0}(\hat{w}_n)\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is the bounded Palais–Smale sequence at the level ![]() $c_{V_0}$. Now, let
$c_{V_0}$. Now, let ![]() $v_n :=m_{V_0}(\hat{w}_n)$. According to theorem 3.5, we see that there exist a sequence
$v_n :=m_{V_0}(\hat{w}_n)$. According to theorem 3.5, we see that there exist a sequence  $\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ and
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ and ![]() $0 \neq \hat{v} \in {X_{V_0}}$ such that
$0 \neq \hat{v} \in {X_{V_0}}$ such that
 \begin{align}
\begin{cases}
\hat{v}_n(\cdot) :=v_n(\cdot + y_n) \xrightarrow w \hat{v} \quad & \ \text{in } {X_{V_0}} \ \text{as } n \rightarrow \infty,\\
I_{V_0}(\hat{v}_n) = c_{V_0} + o_n(1),\ I_{V_0}'(\hat{v}_n) = o_n(1) \quad &\ \text{as } n \rightarrow \infty,\\
I_{V_0}(\hat{v}) = c_{V_0},\ I_{V_0}'(\hat{v}) = 0.
\end{cases}
\end{align}
\begin{align}
\begin{cases}
\hat{v}_n(\cdot) :=v_n(\cdot + y_n) \xrightarrow w \hat{v} \quad & \ \text{in } {X_{V_0}} \ \text{as } n \rightarrow \infty,\\
I_{V_0}(\hat{v}_n) = c_{V_0} + o_n(1),\ I_{V_0}'(\hat{v}_n) = o_n(1) \quad &\ \text{as } n \rightarrow \infty,\\
I_{V_0}(\hat{v}) = c_{V_0},\ I_{V_0}'(\hat{v}) = 0.
\end{cases}
\end{align} Set ![]() $\widetilde{v}_n := \hat{v}_n - \hat{v}$. Applying lemma 2.10, the Hölder inequality, and (3.3), we can deduce that
$\widetilde{v}_n := \hat{v}_n - \hat{v}$. Applying lemma 2.10, the Hölder inequality, and (3.3), we can deduce that
 \begin{align*}I_{V_0}(\widetilde{v}_n) = o_n(1) \quad \ \text{and }\quad I_{V_0}'(\widetilde{v}_n) = o_n(1) \ \text{as } n \rightarrow \infty.\end{align*}
\begin{align*}I_{V_0}(\widetilde{v}_n) = o_n(1) \quad \ \text{and }\quad I_{V_0}'(\widetilde{v}_n) = o_n(1) \ \text{as } n \rightarrow \infty.\end{align*} Consequently, ![]() $\widetilde{v}_n \rightarrow 0$ in
$\widetilde{v}_n \rightarrow 0$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$, that is,
$n \rightarrow \infty$, that is, ![]() $\hat{v}_n \rightarrow \hat{v}$ in
$\hat{v}_n \rightarrow \hat{v}$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$. From lemma 3.1 (c) and (3.3), we infer that
$n \rightarrow \infty$. From lemma 3.1 (c) and (3.3), we infer that ![]() $u_n(\cdot + y_n) \rightarrow \hat{v} \in \mathcal{M}_{V_0}$ as
$u_n(\cdot + y_n) \rightarrow \hat{v} \in \mathcal{M}_{V_0}$ as ![]() $n \rightarrow \infty$. So, we now complete the proof.
$n \rightarrow \infty$. So, we now complete the proof.
4. The barycenter map
Next, we need to establish a relationship between the topology of M and the number of positive solutions for problem (2.2). To this end, we first choose δ > 0 such that
 \begin{align}
M_\delta := \left\{x \in \mathbb{R}^N : {\mathrm{dist}\,} (x,M) \leqslant \delta\right\} \subset \Lambda
\end{align}
\begin{align}
M_\delta := \left\{x \in \mathbb{R}^N : {\mathrm{dist}\,} (x,M) \leqslant \delta\right\} \subset \Lambda
\end{align} and take ![]() $\eta \in C^\infty([0, +\infty),[0,1])$ non-increasing satisfying
$\eta \in C^\infty([0, +\infty),[0,1])$ non-increasing satisfying ![]() $\eta(t) = 1$ for
$\eta(t) = 1$ for ![]() $t \in (0,\delta / 2)$,
$t \in (0,\delta / 2)$, ![]() $\eta(t) = 0$ for
$\eta(t) = 0$ for ![]() $t \in [\delta, + \infty)$, and
$t \in [\delta, + \infty)$, and ![]() $|\eta'(t)| \leqslant C$ for some constant C > 0.
$|\eta'(t)| \leqslant C$ for some constant C > 0.
Let ω be a positive ground state solution to the autonomous problem (3.1). For any ![]() $y \in M$, we define the following function:
$y \in M$, we define the following function:
 \begin{align*}\Psi_{\varepsilon,y}(x) := \eta (|\varepsilon x - y|) \omega\left(\frac{\varepsilon x - y}{\varepsilon}\right)\end{align*}
\begin{align*}\Psi_{\varepsilon,y}(x) := \eta (|\varepsilon x - y|) \omega\left(\frac{\varepsilon x - y}{\varepsilon}\right)\end{align*} with the unique number ![]() $t_\varepsilon \gt 0$ satisfying
$t_\varepsilon \gt 0$ satisfying
 \begin{align*}\max_{t \geqslant 0} J_\varepsilon(t \Psi_{\varepsilon,y}) = J_\varepsilon(t_\varepsilon \Psi_{\varepsilon,y}),\end{align*}
\begin{align*}\max_{t \geqslant 0} J_\varepsilon(t \Psi_{\varepsilon,y}) = J_\varepsilon(t_\varepsilon \Psi_{\varepsilon,y}),\end{align*} and let us consider the mapping ![]() $\Phi_\varepsilon : M \mapsto \mathcal{N_\varepsilon}$ defined by
$\Phi_\varepsilon : M \mapsto \mathcal{N_\varepsilon}$ defined by
Lemma 4.1. The mapping ![]() $\Phi_\varepsilon$ verifies the following property:
$\Phi_\varepsilon$ verifies the following property:
 \begin{align*}\lim_{\varepsilon \rightarrow 0} J_\varepsilon(\Phi_\varepsilon(y)) = c_{V_0} \ \text{uniformly in } y \in M.\end{align*}
\begin{align*}\lim_{\varepsilon \rightarrow 0} J_\varepsilon(\Phi_\varepsilon(y)) = c_{V_0} \ \text{uniformly in } y \in M.\end{align*}Proof. Arguing by contradiction, we may assume that there exist ![]() $\delta_0 \gt 0$,
$\delta_0 \gt 0$, ![]() $\left\{y_n\right\}_{n \in \mathbb{N}} \subset M$, and
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset M$, and ![]() $\varepsilon_n \rightarrow 0$ in
$\varepsilon_n \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$ such that
$n \rightarrow \infty$ such that
 \begin{align}
\left|J_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) - c_{V_0} \right| \geqslant \delta_0.
\end{align}
\begin{align}
\left|J_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) - c_{V_0} \right| \geqslant \delta_0.
\end{align} We first note that for each ![]() $ n \in \mathbb{N}$ and for all
$ n \in \mathbb{N}$ and for all  $ z \in B_{\frac{\delta}{\varepsilon_n}}$,
$ z \in B_{\frac{\delta}{\varepsilon_n}}$, ![]() $ \varepsilon_n z\in B_\delta$, and hence
$ \varepsilon_n z\in B_\delta$, and hence ![]() $\varepsilon_n z + y_n \in B_\delta(y_n) \subset M_\delta \subset \Lambda$.
$\varepsilon_n z + y_n \in B_\delta(y_n) \subset M_\delta \subset \Lambda$.
Applying the change of variable ![]() $z = (\varepsilon_n x - y_n) / {\varepsilon_n}$ and recalling that G = F in Λ and
$z = (\varepsilon_n x - y_n) / {\varepsilon_n}$ and recalling that G = F in Λ and ![]() $\eta(t) = 0$ for
$\eta(t) = 0$ for ![]() $t \geqslant \delta$, we have
$t \geqslant \delta$, we have
 \begin{align}
J_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) & = \frac{{t_{\varepsilon_n}^p}}{p} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n}, p}^p + \frac{{t_{\varepsilon_n}^q}}{q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n}, q}^q\nonumber\\
& - \frac{1}{2}\int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * G(\varepsilon_n x, t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n})\right)G(\varepsilon_n x, t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n}) dx\nonumber\\
& = \frac{{t_{\varepsilon_n}^p}}{p} \left([\eta(|\varepsilon_n \cdot|) \omega]_{s,p}^p + \int_{\mathbb{R}^N} V(\varepsilon_n z + y_n)(\eta(|\varepsilon_n z|) \omega(z))^p dz\right)\nonumber\\
& + \frac{{t_{\varepsilon_n}^q}}{q} \left([\eta(|\varepsilon_n \cdot|) \omega]_{s,q}^q + \int_{\mathbb{R}^N} V(\varepsilon_n z + y_n)(\eta(|\varepsilon_n z|) \omega(z))^q dz\right)\nonumber\\
& - \frac{1}{2}\int_{\mathbb{R}^N} \left(\frac{1}{|z|^\mu} * F(t_{\varepsilon_n} \eta(|\varepsilon_n z|) \omega(z))\right) F(t_{\varepsilon_n} \eta(|\varepsilon_n z|) \omega(z)) dz.
\end{align}
\begin{align}
J_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) & = \frac{{t_{\varepsilon_n}^p}}{p} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n}, p}^p + \frac{{t_{\varepsilon_n}^q}}{q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n}, q}^q\nonumber\\
& - \frac{1}{2}\int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * G(\varepsilon_n x, t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n})\right)G(\varepsilon_n x, t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n}) dx\nonumber\\
& = \frac{{t_{\varepsilon_n}^p}}{p} \left([\eta(|\varepsilon_n \cdot|) \omega]_{s,p}^p + \int_{\mathbb{R}^N} V(\varepsilon_n z + y_n)(\eta(|\varepsilon_n z|) \omega(z))^p dz\right)\nonumber\\
& + \frac{{t_{\varepsilon_n}^q}}{q} \left([\eta(|\varepsilon_n \cdot|) \omega]_{s,q}^q + \int_{\mathbb{R}^N} V(\varepsilon_n z + y_n)(\eta(|\varepsilon_n z|) \omega(z))^q dz\right)\nonumber\\
& - \frac{1}{2}\int_{\mathbb{R}^N} \left(\frac{1}{|z|^\mu} * F(t_{\varepsilon_n} \eta(|\varepsilon_n z|) \omega(z))\right) F(t_{\varepsilon_n} \eta(|\varepsilon_n z|) \omega(z)) dz.
\end{align} Next, we prove that the sequence ![]() $\left\{t_{\varepsilon_n}\right\}_{n \in \mathbb{N}} \subset \mathbb{R}$ verifies
$\left\{t_{\varepsilon_n}\right\}_{n \in \mathbb{N}} \subset \mathbb{R}$ verifies ![]() $t_{\varepsilon_n} \rightarrow 1$ in
$t_{\varepsilon_n} \rightarrow 1$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty.$ Using the definition of
$n \rightarrow \infty.$ Using the definition of ![]() $t_{\varepsilon_n}$, we see that
$t_{\varepsilon_n}$, we see that ![]() $t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n} \in \mathcal{N}_{\varepsilon_n}$, that is,
$t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n} \in \mathcal{N}_{\varepsilon_n}$, that is,
 \begin{align}
& t_{\varepsilon_n}^{p - q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},p}^p + \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},q}^q \nonumber\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n})\right) \frac{f(t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n}) \Psi_{\varepsilon_n,y_n}}{t_{\varepsilon_n}^{q - 1}} dx\nonumber\\
& (\text{on account of the fact that } g = f ,\ G = F\ \text{on } \Lambda)\nonumber\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|z|^\mu} * F(t_{\varepsilon_n} \eta(|\varepsilon_n z|) \omega(z))\right) \frac{f(t_{\varepsilon_n} \eta(|\varepsilon_n z|) \omega(z)) \eta(|\varepsilon_n z|) \omega(z)}{t_{\varepsilon_n}^{q - 1}} dz.
\end{align}
\begin{align}
& t_{\varepsilon_n}^{p - q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},p}^p + \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},q}^q \nonumber\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n})\right) \frac{f(t_{\varepsilon_n} \Psi_{\varepsilon_n,y_n}) \Psi_{\varepsilon_n,y_n}}{t_{\varepsilon_n}^{q - 1}} dx\nonumber\\
& (\text{on account of the fact that } g = f ,\ G = F\ \text{on } \Lambda)\nonumber\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|z|^\mu} * F(t_{\varepsilon_n} \eta(|\varepsilon_n z|) \omega(z))\right) \frac{f(t_{\varepsilon_n} \eta(|\varepsilon_n z|) \omega(z)) \eta(|\varepsilon_n z|) \omega(z)}{t_{\varepsilon_n}^{q - 1}} dz.
\end{align} Taking into account ![]() $\eta
(|x|) = 1$ for
$\eta
(|x|) = 1$ for  $x \in B_{\frac{\delta}{2}}$ and
$x \in B_{\frac{\delta}{2}}$ and  $B_{\frac{\delta}{2}} \subset B_{\frac{\delta}{\varepsilon_n}}$ for
$B_{\frac{\delta}{2}} \subset B_{\frac{\delta}{\varepsilon_n}}$ for ![]() $n \in \mathbb{N}$ large enough, we deduce from (4.4) that
$n \in \mathbb{N}$ large enough, we deduce from (4.4) that
 \begin{align*}t_{\varepsilon_n}^{p - q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},p}^p + \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},q}^q \geqslant \int_{B_{\frac{\delta}{2}}} \int_{B_{\frac{\delta}{2}}} \frac{F(t_{\varepsilon_n} \omega(x)) f(t_{\varepsilon_n} \omega(z)) \omega(z)}{t_{\varepsilon_n}^{q - 1}|z - x|^\mu} dxdz.\end{align*}
\begin{align*}t_{\varepsilon_n}^{p - q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},p}^p + \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},q}^q \geqslant \int_{B_{\frac{\delta}{2}}} \int_{B_{\frac{\delta}{2}}} \frac{F(t_{\varepsilon_n} \omega(x)) f(t_{\varepsilon_n} \omega(z)) \omega(z)}{t_{\varepsilon_n}^{q - 1}|z - x|^\mu} dxdz.\end{align*} On the other hand, ω is a continuous and positive function in ![]() $\mathbb{R}^N$, so there exists
$\mathbb{R}^N$, so there exists ![]() $\bar{z} \in \mathbb{R}^N$ such that
$\bar{z} \in \mathbb{R}^N$ such that
 \begin{align*}\omega(\bar{z}) = \min_{z \in \overline{B}_{\frac{\delta}{2}}} \omega(z) \gt 0.\end{align*}
\begin{align*}\omega(\bar{z}) = \min_{z \in \overline{B}_{\frac{\delta}{2}}} \omega(z) \gt 0.\end{align*} Thus, we deduce from hypothesis ![]() $(f_4)$ that
$(f_4)$ that
 \begin{align}
t_{\varepsilon_n}^{p - q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},p}^p + \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},q}^q \geqslant \delta^{- \mu} \left|B_{\frac{\delta}{2}}\right|^2 \frac{F(t_{\varepsilon_n} \omega(\bar{z})) f(t_{\varepsilon_n} \omega(\bar{z}))}{\left(t_{\varepsilon_n} \omega(\bar{z})\right)^{q - 1}} \omega(\bar{z})^q.
\end{align}
\begin{align}
t_{\varepsilon_n}^{p - q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},p}^p + \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},q}^q \geqslant \delta^{- \mu} \left|B_{\frac{\delta}{2}}\right|^2 \frac{F(t_{\varepsilon_n} \omega(\bar{z})) f(t_{\varepsilon_n} \omega(\bar{z}))}{\left(t_{\varepsilon_n} \omega(\bar{z})\right)^{q - 1}} \omega(\bar{z})^q.
\end{align}According to the Dominated Convergence Theorem and lemma 2.2 in the study by Ambrosio [Reference Ambrosio7], we can deduce that
and
 \begin{align}
\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\Psi_{\varepsilon_n,y_n})\right) F(\Psi_{\varepsilon_n,y_n}) dx \rightarrow \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\omega)\right) F(\omega) dx \ \text{in } \mathbb{R} \ \text{as } n \rightarrow \infty.
\end{align}
\begin{align}
\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\Psi_{\varepsilon_n,y_n})\right) F(\Psi_{\varepsilon_n,y_n}) dx \rightarrow \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\omega)\right) F(\omega) dx \ \text{in } \mathbb{R} \ \text{as } n \rightarrow \infty.
\end{align} Therefore, if ![]() $t_{\varepsilon_n} \rightarrow + \infty$, we can conclude that the left-hand side of (4.5) satisfies the following property:
$t_{\varepsilon_n} \rightarrow + \infty$, we can conclude that the left-hand side of (4.5) satisfies the following property:
 \begin{align}
\lim_{n \rightarrow \infty}\left(t_{\varepsilon_n}^{p - q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},p}^p + \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},q}^q\right) = \|\omega\|_{V_0,q}^q,
\end{align}
\begin{align}
\lim_{n \rightarrow \infty}\left(t_{\varepsilon_n}^{p - q} \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},p}^p + \|\Psi_{\varepsilon_n,y_n}\|_{V_{\varepsilon_n},q}^q\right) = \|\omega\|_{V_0,q}^q,
\end{align} since q > p. On the other hand, we deduce from hypothesis ![]() $(f_3)$ that
$(f_3)$ that
 \begin{align}
\lim_{n \rightarrow \infty} \frac{F(t_{\varepsilon_n} \omega(\bar{z}))}{(t_{\varepsilon_n} \omega(\bar{z}))^{\frac{q}{2}}} = \lim_{n \rightarrow \infty} \frac{f(t_{\varepsilon_n} \omega(\bar{z}))}{(t_{\varepsilon_n} \omega(\bar{z}))^{\frac{q}{2} - 1}} = + \infty.
\end{align}
\begin{align}
\lim_{n \rightarrow \infty} \frac{F(t_{\varepsilon_n} \omega(\bar{z}))}{(t_{\varepsilon_n} \omega(\bar{z}))^{\frac{q}{2}}} = \lim_{n \rightarrow \infty} \frac{f(t_{\varepsilon_n} \omega(\bar{z}))}{(t_{\varepsilon_n} \omega(\bar{z}))^{\frac{q}{2} - 1}} = + \infty.
\end{align} From (4.5), (4.8), and (4.9) we get a contradiction. Then, we pass to a subsequence and assume that there exists t 0 such that ![]() $t_{\varepsilon_n} \rightarrow t_0 \geqslant 0$. In addition, applying (4.4) and (4.6) and combining with
$t_{\varepsilon_n} \rightarrow t_0 \geqslant 0$. In addition, applying (4.4) and (4.6) and combining with ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, we deduce that
$(f_2)$, we deduce that ![]() $t_0 \gt 0$.
$t_0 \gt 0$.
In (4.4), we pass to the limit as ![]() $n \rightarrow \infty$, and then we can use (4.6) and the Dominated Convergence Theorem to infer that
$n \rightarrow \infty$, and then we can use (4.6) and the Dominated Convergence Theorem to infer that
 \begin{align}
t_0^{p - q} \|\omega\|_{V_0,p}^p + \|\omega\|_{V_0,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(t_0 \omega)\right) \frac{f(t_0 \omega)}{t_0^{q - 1}} \omega dx.
\end{align}
\begin{align}
t_0^{p - q} \|\omega\|_{V_0,p}^p + \|\omega\|_{V_0,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(t_0 \omega)\right) \frac{f(t_0 \omega)}{t_0^{q - 1}} \omega dx.
\end{align} Due to ![]() $\omega \in \mathcal{M}_{V_0}$, we derive that
$\omega \in \mathcal{M}_{V_0}$, we derive that
 \begin{align}
\|\omega\|_{V_0,p}^p + \|\omega\|_{V_0,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\omega)\right) \frac{f(\omega)}{t_0^{q - 1}} \omega dx.
\end{align}
\begin{align}
\|\omega\|_{V_0,p}^p + \|\omega\|_{V_0,q}^q = \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\omega)\right) \frac{f(\omega)}{t_0^{q - 1}} \omega dx.
\end{align} From the fact that the functions  $\frac{F(t)}{t^{\frac{q}{2}}}$ and
$\frac{F(t)}{t^{\frac{q}{2}}}$ and  $\frac{f(t)}{t^{\frac{q}{2} - 1}}$ are increasing for t > 0, together with (4.10) and (4.11), it follows that
$\frac{f(t)}{t^{\frac{q}{2} - 1}}$ are increasing for t > 0, together with (4.10) and (4.11), it follows that ![]() $t_0 = 1$.
$t_0 = 1$.
In (4.3), we pass to the limit as ![]() $n \rightarrow \infty$, and together with (4.7), we have
$n \rightarrow \infty$, and together with (4.7), we have
 \begin{align*}\lim_{n \rightarrow \infty} J_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) = I_{V_0}(\omega) = c_{V_0}.\end{align*}
\begin{align*}\lim_{n \rightarrow \infty} J_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) = I_{V_0}(\omega) = c_{V_0}.\end{align*}This is a contradiction, since (4.2). So, we complete the proof of the lemma.
Let us consider the function ![]() $h : \mathbb{R}^+ \mapsto \mathbb{R}^+$ such that
$h : \mathbb{R}^+ \mapsto \mathbb{R}^+$ such that  $h(\varepsilon) := \sup_{y \in M} \left|J_\varepsilon(\Phi_\varepsilon(y)) - c_{V_0}\right|$ for all ɛ > 0. Then, we define the following subset of
$h(\varepsilon) := \sup_{y \in M} \left|J_\varepsilon(\Phi_\varepsilon(y)) - c_{V_0}\right|$ for all ɛ > 0. Then, we define the following subset of ![]() $\mathcal{N}_\varepsilon$:
$\mathcal{N}_\varepsilon$:
 \begin{align*}\hat{\mathcal{N}}_\varepsilon := \left\{u \in \mathcal{N}_\varepsilon : J_\varepsilon(u) \leqslant c_{V_0} + h(\varepsilon)\right\}.\end{align*}
\begin{align*}\hat{\mathcal{N}}_\varepsilon := \left\{u \in \mathcal{N}_\varepsilon : J_\varepsilon(u) \leqslant c_{V_0} + h(\varepsilon)\right\}.\end{align*} From lemma 4.1, it follows that ![]() $h(\varepsilon) \rightarrow 0$ as
$h(\varepsilon) \rightarrow 0$ as ![]() $\varepsilon \rightarrow 0$. Additionally, we deduce from the definition of h that
$\varepsilon \rightarrow 0$. Additionally, we deduce from the definition of h that ![]() $\Phi_\varepsilon(y) \in \hat{\mathcal{N}}_\varepsilon$ for any
$\Phi_\varepsilon(y) \in \hat{\mathcal{N}}_\varepsilon$ for any ![]() $y \in M$ and ɛ > 0, and so
$y \in M$ and ɛ > 0, and so ![]() $\hat{\mathcal{N}}_\varepsilon \neq \emptyset$.
$\hat{\mathcal{N}}_\varepsilon \neq \emptyset$.
For any δ > 0 given by (4.1), let us choose ![]() $\rho := \rho(\delta) \gt 0$ such that
$\rho := \rho(\delta) \gt 0$ such that ![]() $M_\delta \subset B_\rho$. Then, we introduce the map
$M_\delta \subset B_\rho$. Then, we introduce the map ![]() $\zeta : \mathbb{R}^N \mapsto \mathbb{R}^N$ defined by
$\zeta : \mathbb{R}^N \mapsto \mathbb{R}^N$ defined by
 \begin{align*}
\zeta(x) :=
\begin{cases}
x \quad & \ \text{if } |x| \lt \rho,\\
\frac{\rho x}{|x|} \quad & \ \text{if } |x| \geqslant \rho.
\end{cases}
\end{align*}
\begin{align*}
\zeta(x) :=
\begin{cases}
x \quad & \ \text{if } |x| \lt \rho,\\
\frac{\rho x}{|x|} \quad & \ \text{if } |x| \geqslant \rho.
\end{cases}
\end{align*} Now, we introduce the following barycenter map ![]() $\beta_\varepsilon : \mathcal{N}_\varepsilon \mapsto \mathbb{R}^N$ defined by
$\beta_\varepsilon : \mathcal{N}_\varepsilon \mapsto \mathbb{R}^N$ defined by
 \begin{align*}\beta_\varepsilon(u) := \frac{\int_{\mathbb{R}^N}\zeta(\varepsilon x) \left(|u|^p + |u|^q\right) dx}{\int_{\mathbb{R}^N} \left(|u|^p + |u|^q\right) dx}\end{align*}
\begin{align*}\beta_\varepsilon(u) := \frac{\int_{\mathbb{R}^N}\zeta(\varepsilon x) \left(|u|^p + |u|^q\right) dx}{\int_{\mathbb{R}^N} \left(|u|^p + |u|^q\right) dx}\end{align*} for all ![]() $u \in \mathcal{N}_\varepsilon$.
$u \in \mathcal{N}_\varepsilon$.
Then, from the above information, we can give the following lemma.
Lemma 4.2. The function βɛ has the following property:
 \begin{align*}\lim_{\varepsilon \rightarrow 0} \beta_\varepsilon(\Phi_\varepsilon(y)) = y \ \text{uniformly in } y \in M.\end{align*}
\begin{align*}\lim_{\varepsilon \rightarrow 0} \beta_\varepsilon(\Phi_\varepsilon(y)) = y \ \text{uniformly in } y \in M.\end{align*}Proof. Arguing by contradiction, assume that there exist ![]() $\delta_0 \gt 0$,
$\delta_0 \gt 0$, ![]() $\left\{y_n\right\}_{n \in \mathbb{N}} \subset M$, and
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset M$, and ![]() $\varepsilon_n \rightarrow 0$ in
$\varepsilon_n \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$ such that
$n \rightarrow \infty$ such that
Employing the definitions of ![]() $\Phi_{\varepsilon_n}$,
$\Phi_{\varepsilon_n}$, ![]() $\beta_{\varepsilon_n}$, and ζ and using the change of variable
$\beta_{\varepsilon_n}$, and ζ and using the change of variable ![]() $z = (\varepsilon_n x - y_n) / \varepsilon_n$, we can conclude that
$z = (\varepsilon_n x - y_n) / \varepsilon_n$, we can conclude that
 \begin{align*}\beta_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) = y_n + \frac{\int_{\mathbb{R}^N} \left(\zeta(\varepsilon_n z + y_n) - y_n \right) \left(|\eta(|\varepsilon_n z|) \omega(z)|^p + |\eta(|\varepsilon_n z|) \omega(z)|^q\right) dz}{\int_{\mathbb{R}^N} \left(|\eta(|\varepsilon_n z|) \omega(z)|^p + |\eta(|\varepsilon_n z|) \omega(z)|^q\right) dz}.\end{align*}
\begin{align*}\beta_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) = y_n + \frac{\int_{\mathbb{R}^N} \left(\zeta(\varepsilon_n z + y_n) - y_n \right) \left(|\eta(|\varepsilon_n z|) \omega(z)|^p + |\eta(|\varepsilon_n z|) \omega(z)|^q\right) dz}{\int_{\mathbb{R}^N} \left(|\eta(|\varepsilon_n z|) \omega(z)|^p + |\eta(|\varepsilon_n z|) \omega(z)|^q\right) dz}.\end{align*} On account of ![]() $\left\{y_n\right\}_{n \in \mathbb{N}} \subset M \subset M_\delta$, combining the Dominated Convergence Theorem, we can derive that
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset M \subset M_\delta$, combining the Dominated Convergence Theorem, we can derive that
 \begin{align*}\lim_{n \rightarrow \infty} |\beta_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) - y_n| = 0,\end{align*}
\begin{align*}\lim_{n \rightarrow \infty} |\beta_{\varepsilon_n}(\Phi_{\varepsilon_n}(y_n)) - y_n| = 0,\end{align*}which contradicts relation (4.12). This proof is now complete.
Lemma 4.3. Let ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq).$ Assume that the sequences
$\nu \lt (N - \mu) q / (N - sq).$ Assume that the sequences ![]() $\left\{\varepsilon_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}$ and
$\left\{\varepsilon_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}$ and ![]() $\left\{u_n\right\}_{n \in
\mathbb{N}} \subset \mathcal{N}_{\varepsilon_n}$ satisfy
$\left\{u_n\right\}_{n \in
\mathbb{N}} \subset \mathcal{N}_{\varepsilon_n}$ satisfy ![]() $\varepsilon_n \rightarrow 0$ in
$\varepsilon_n \rightarrow 0$ in ![]() $\mathbb{R}$ and
$\mathbb{R}$ and ![]() $J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in
$J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$; then, there is a sequence
$n \rightarrow \infty$; then, there is a sequence  $\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that the sequence
$\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that the sequence ![]() $\left\{\hat{u}_n(x) := u_n(x + \hat{y}_n)\right\}_{n \in \mathbb{N}}$ admits a subsequence which converges in
$\left\{\hat{u}_n(x) := u_n(x + \hat{y}_n)\right\}_{n \in \mathbb{N}}$ admits a subsequence which converges in ![]() ${X_{V_0}}.$ Furthermore, the sequence
${X_{V_0}}.$ Furthermore, the sequence  $ \left\{y_n := \varepsilon_n \hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ has a subsequence
$ \left\{y_n := \varepsilon_n \hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ has a subsequence ![]() $\left\{y_n\right\}_{n \in \mathbb{N}}$
$\left\{y_n\right\}_{n \in \mathbb{N}}$ ![]() $($still denoted by itself
$($still denoted by itself ![]() $)$ such that
$)$ such that ![]() $y_n \rightarrow y_0 \in M$ as
$y_n \rightarrow y_0 \in M$ as ![]() $n \rightarrow \infty.$
$n \rightarrow \infty.$
Proof. It is easy to verify that ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset X_{V_0}$ is bounded. Then, using lemma 3.4, we know that there exist a sequence
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset X_{V_0}$ is bounded. Then, using lemma 3.4, we know that there exist a sequence  $\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ and some constants
$\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ and some constants ![]() $R,$ α > 0 such that
$R,$ α > 0 such that
 \begin{align*}\liminf_{n \rightarrow \infty} \int_{B_R(\hat{y}_n)} |u_n|^q dx \geqslant \alpha.\end{align*}
\begin{align*}\liminf_{n \rightarrow \infty} \int_{B_R(\hat{y}_n)} |u_n|^q dx \geqslant \alpha.\end{align*} Let ![]() $\hat{u}_n(x) := u_n(x + \hat{y}_n)$. Consequently,
$\hat{u}_n(x) := u_n(x + \hat{y}_n)$. Consequently, ![]() $\left\{\hat{u}_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is bounded, and so passing to a subsequence, we can suppose that there exists some
$\left\{\hat{u}_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is bounded, and so passing to a subsequence, we can suppose that there exists some ![]() $0 \neq \hat{u} \in {X_{V_0}}$ such that
$0 \neq \hat{u} \in {X_{V_0}}$ such that ![]() $\hat{u}_n \xrightarrow w \hat{u}$ in
$\hat{u}_n \xrightarrow w \hat{u}$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$. Let
$n \rightarrow \infty$. Let ![]() $t_n \gt 0$ be such that
$t_n \gt 0$ be such that ![]() $\hat{v}_n := t_n \hat{u}_n \in \mathcal{M}_{V_0}$, and let
$\hat{v}_n := t_n \hat{u}_n \in \mathcal{M}_{V_0}$, and let ![]() $y_n :=\varepsilon_n \hat{y}_n$. Thus, we deduce that
$y_n :=\varepsilon_n \hat{y}_n$. Thus, we deduce that
 \begin{align*}
c_{V_0}& \leqslant I_{V_0}(\hat{v}_n) \ (\text{from the definition of } c_{V_0})\\
& \leqslant \frac{1}{p} [\hat{v}_n]_{s,p}^p + \frac{1}{q} [\hat{v}_n]_{s,q}^q + \int_{\mathbb{R}^N} V(\varepsilon_n x + y_n) \left(\frac{1}{p} |\hat{v}_n|^p + \frac{1}{q}|\hat{v}_n|^q\right) dx\\
& - \frac{1}{2}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\hat{v}_n)\right) F(\hat{v}_n) dx\\
& \leqslant \frac{t_n^p}{p} [u_n]_{s,p}^p + \frac{t_n^q}{q} [u_n]_{s,q}^q + \int_{\mathbb{R}^N} V(\varepsilon_n x) \left(\frac{t_n^p}{p}|u_n|^p + \frac{t_n^q}{q}|u_n|^q\right) dx\\
& - \frac{1}{2}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, t_n u_n)\right) G(\varepsilon x, t_n u_n) dx \ (\text{by } (g_2))\\
& = J_{\varepsilon_n}(t_n u_n) \leqslant J_{\varepsilon_n}(u_n)\ (\text{since } u_n \in \mathcal{N}_{\varepsilon_n})\\
& = c_{V_0} + o_n(1) \ \text{as } n \rightarrow \infty.
\end{align*}
\begin{align*}
c_{V_0}& \leqslant I_{V_0}(\hat{v}_n) \ (\text{from the definition of } c_{V_0})\\
& \leqslant \frac{1}{p} [\hat{v}_n]_{s,p}^p + \frac{1}{q} [\hat{v}_n]_{s,q}^q + \int_{\mathbb{R}^N} V(\varepsilon_n x + y_n) \left(\frac{1}{p} |\hat{v}_n|^p + \frac{1}{q}|\hat{v}_n|^q\right) dx\\
& - \frac{1}{2}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\hat{v}_n)\right) F(\hat{v}_n) dx\\
& \leqslant \frac{t_n^p}{p} [u_n]_{s,p}^p + \frac{t_n^q}{q} [u_n]_{s,q}^q + \int_{\mathbb{R}^N} V(\varepsilon_n x) \left(\frac{t_n^p}{p}|u_n|^p + \frac{t_n^q}{q}|u_n|^q\right) dx\\
& - \frac{1}{2}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon x, t_n u_n)\right) G(\varepsilon x, t_n u_n) dx \ (\text{by } (g_2))\\
& = J_{\varepsilon_n}(t_n u_n) \leqslant J_{\varepsilon_n}(u_n)\ (\text{since } u_n \in \mathcal{N}_{\varepsilon_n})\\
& = c_{V_0} + o_n(1) \ \text{as } n \rightarrow \infty.
\end{align*} This implies that ![]() $I_{V_0}(\hat{v}_n) \rightarrow c_{V_0}$ in
$I_{V_0}(\hat{v}_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$ and
$n \rightarrow \infty$ and ![]() $\hat{v}_n \in \mathcal{M}_{V_0}.$ Clearly, the sequence
$\hat{v}_n \in \mathcal{M}_{V_0}.$ Clearly, the sequence ![]() $\left\{\hat{v}_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is bounded. Therefore, up to a subsequence if necessary, still denoted by itself, we may assume that there exists
$\left\{\hat{v}_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ is bounded. Therefore, up to a subsequence if necessary, still denoted by itself, we may assume that there exists ![]() $\hat{v} \in {X_{V_0}}$ such that
$\hat{v} \in {X_{V_0}}$ such that ![]() $\hat{v}_n \xrightarrow w \hat{v}$ in
$\hat{v}_n \xrightarrow w \hat{v}$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$. It is easy to see that the sequence
$n \rightarrow \infty$. It is easy to see that the sequence ![]() $\left\{t_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}$ is bounded, and it holds that
$\left\{t_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}$ is bounded, and it holds that ![]() $t_n \rightarrow t_0 \geqslant 0$ as
$t_n \rightarrow t_0 \geqslant 0$ as ![]() $n \rightarrow \infty$. Indeed,
$n \rightarrow \infty$. Indeed, ![]() $t_0 \gt 0$. Otherwise,
$t_0 \gt 0$. Otherwise, ![]() $t_0 = 0$, so, we infer from the boundedness of the sequence
$t_0 = 0$, so, we infer from the boundedness of the sequence ![]() $\left\{\hat{v}_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ that
$\left\{\hat{v}_n\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ that  $\|\hat{v}_n\|_{X_{V_0}} = t_n \|\hat{u}_n\|_{X_{V_0}} \rightarrow 0$ in
$\|\hat{v}_n\|_{X_{V_0}} = t_n \|\hat{u}_n\|_{X_{V_0}} \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$, and so
$n \rightarrow \infty$, and so ![]() $I_{V_0}(\hat{v}_n) \rightarrow 0$ in
$I_{V_0}(\hat{v}_n) \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$, but this is impossible, since
$n \rightarrow \infty$, but this is impossible, since ![]() $c_{V_0} \gt 0$. Thus,
$c_{V_0} \gt 0$. Thus, ![]() $t_0 \gt 0$. We deduce from the uniqueness of the weak limit that
$t_0 \gt 0$. We deduce from the uniqueness of the weak limit that ![]() $\hat{v} = t_0 \hat{u}$ and
$\hat{v} = t_0 \hat{u}$ and ![]() $\hat{u} \neq 0$. Then, from lemma 3.6, it follows that
$\hat{u} \neq 0$. Then, from lemma 3.6, it follows that
and so ![]() $\hat{u}_n \rightarrow \hat{u}$ in
$\hat{u}_n \rightarrow \hat{u}$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$. Moreover,
$n \rightarrow \infty$. Moreover, ![]() $I_{V_0}(\hat{v}) = c_{V_0}$ and
$I_{V_0}(\hat{v}) = c_{V_0}$ and  $\langle I_{V_0}'(\hat{v}), \hat{v} \rangle = 0$.
$\langle I_{V_0}'(\hat{v}), \hat{v} \rangle = 0$.
Next, we shall prove that the sequence  $\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ has a subsequence, still denoted by itself, such that
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ has a subsequence, still denoted by itself, such that ![]() $y_n \rightarrow y_0 \in M$ as
$y_n \rightarrow y_0 \in M$ as ![]() $n \rightarrow \infty$. We first show the boundedness of the sequence
$n \rightarrow \infty$. We first show the boundedness of the sequence  $\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$. Otherwise, the sequence
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$. Otherwise, the sequence  $\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ is not bounded. So, we may assume that there exists a subsequence, still denoted by itself, such that
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ is not bounded. So, we may assume that there exists a subsequence, still denoted by itself, such that ![]() $|y_n| \rightarrow + \infty$ in
$|y_n| \rightarrow + \infty$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$. Then, we choose R > 0 large enough such that
$n \rightarrow \infty$. Then, we choose R > 0 large enough such that ![]() $\Lambda \subset B_R$, we may suppose that
$\Lambda \subset B_R$, we may suppose that ![]() $|y_n| \gt 2 R$ for
$|y_n| \gt 2 R$ for ![]() $n \in \mathbb{N}$ sufficiently large, and so for all
$n \in \mathbb{N}$ sufficiently large, and so for all ![]() $x \in B_{R / {\varepsilon_n}}$ we have
$x \in B_{R / {\varepsilon_n}}$ we have
On account of the facts that ![]() $u_n \in \mathcal{N}_{\varepsilon_n}$ and
$u_n \in \mathcal{N}_{\varepsilon_n}$ and ![]() $J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in
$J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$, thus, for
$n \rightarrow \infty$, thus, for ![]() $n \in \mathbb{N}$ large enough, we have that
$n \in \mathbb{N}$ large enough, we have that ![]() $u_n \in \mathcal{B}$. Consequently, from lemma 2.6, it follows that
$u_n \in \mathcal{B}$. Consequently, from lemma 2.6, it follows that
 \begin{align*}\left|\frac{1}{|x|^\mu} * G(\varepsilon_n x, u_n)\right|_{L^\infty(\mathbb{R}^N)} \lt \frac{K}{2} \ \text{for } n \in \mathbb{N} \ \text{large enough}.\end{align*}
\begin{align*}\left|\frac{1}{|x|^\mu} * G(\varepsilon_n x, u_n)\right|_{L^\infty(\mathbb{R}^N)} \lt \frac{K}{2} \ \text{for } n \in \mathbb{N} \ \text{large enough}.\end{align*} Therefore, for ![]() $n \in \mathbb{N}$ large enough, we obtain
$n \in \mathbb{N}$ large enough, we obtain
 \begin{align*}
\|\hat{u}_n\|_{V_0,p}^p + \|\hat{u}_n\|_{V_0,q}^q & \leqslant \frac{K}{2} \int_{\mathbb{R}^N} g(\varepsilon_n x + y_n, \hat{u}_n) \hat{u}_n dx\\
& \leqslant \frac{K}{2} \int_{B_{R / {\varepsilon_n}}} \widetilde{f}(\hat{u}_n) \hat{u}_n dx + \frac{K}{2} \int_{B_{R / {\varepsilon_n}}^c} f(\hat{u}_n) \hat{u}_n dx\\
& \leqslant \frac{K}{2} \int_{B_{R / {\varepsilon_n}}} \frac{V_0}{K} \left(|\hat{u}_n|^p + |\hat{u}_n|^q \right) dx + \frac{K}{2} \int_{B_{R / {\varepsilon_n}}^c} f(\hat{u}_n) \hat{u}_n dx,\\
&\quad (\text{on account of the fact that } \widetilde{f}(\hat{u}_n) \hat{u}_n \\
& \qquad \leqslant \frac{V_0}{K} \left(|\hat{u}_n|^p + |\hat{u}_n|^q \right) \ \text{on } B_{R / {\varepsilon_n}}).
\end{align*}
\begin{align*}
\|\hat{u}_n\|_{V_0,p}^p + \|\hat{u}_n\|_{V_0,q}^q & \leqslant \frac{K}{2} \int_{\mathbb{R}^N} g(\varepsilon_n x + y_n, \hat{u}_n) \hat{u}_n dx\\
& \leqslant \frac{K}{2} \int_{B_{R / {\varepsilon_n}}} \widetilde{f}(\hat{u}_n) \hat{u}_n dx + \frac{K}{2} \int_{B_{R / {\varepsilon_n}}^c} f(\hat{u}_n) \hat{u}_n dx\\
& \leqslant \frac{K}{2} \int_{B_{R / {\varepsilon_n}}} \frac{V_0}{K} \left(|\hat{u}_n|^p + |\hat{u}_n|^q \right) dx + \frac{K}{2} \int_{B_{R / {\varepsilon_n}}^c} f(\hat{u}_n) \hat{u}_n dx,\\
&\quad (\text{on account of the fact that } \widetilde{f}(\hat{u}_n) \hat{u}_n \\
& \qquad \leqslant \frac{V_0}{K} \left(|\hat{u}_n|^p + |\hat{u}_n|^q \right) \ \text{on } B_{R / {\varepsilon_n}}).
\end{align*} Recalling that ![]() $\hat{u}_n \rightarrow \hat{u}$ in
$\hat{u}_n \rightarrow \hat{u}$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$ and using the Dominated Convergence Theorem, we obtain
$n \rightarrow \infty$ and using the Dominated Convergence Theorem, we obtain
 \begin{align*}\int_{B_{R / {\varepsilon_n}}^c} f(\hat{u}_n) \hat{u}_n dx = o_n(1) \ \text{as } n \rightarrow \infty.\end{align*}
\begin{align*}\int_{B_{R / {\varepsilon_n}}^c} f(\hat{u}_n) \hat{u}_n dx = o_n(1) \ \text{as } n \rightarrow \infty.\end{align*}So, we have
 \begin{align*}\frac{1}{2} \left (\|\hat{u}_n\|_{V_0,p}^p + \|\hat{u}_n\|_{V_0,q}^q \right) \leqslant o_n(1) \ \text{as } n \rightarrow \infty.\end{align*}
\begin{align*}\frac{1}{2} \left (\|\hat{u}_n\|_{V_0,p}^p + \|\hat{u}_n\|_{V_0,q}^q \right) \leqslant o_n(1) \ \text{as } n \rightarrow \infty.\end{align*} Using ![]() $\hat{u}_n \rightarrow \hat{u} \neq 0$ in
$\hat{u}_n \rightarrow \hat{u} \neq 0$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$ again, we see that this is a contradiction.
$n \rightarrow \infty$ again, we see that this is a contradiction.
Now, we get the boundedness of the sequence  $\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$. Passing to a subsequence (still denoted by
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$. Passing to a subsequence (still denoted by ![]() $\left\{y_n\right\}_{n \in \mathbb{N}}$), we may assume that there exists
$\left\{y_n\right\}_{n \in \mathbb{N}}$), we may assume that there exists ![]() $y_0 \in \mathbb{R}^N$ such that
$y_0 \in \mathbb{R}^N$ such that ![]() $y_n \rightarrow y_0 \in \overline{\Lambda}$ as
$y_n \rightarrow y_0 \in \overline{\Lambda}$ as ![]() $n \rightarrow \infty$. In fact, if
$n \rightarrow \infty$. In fact, if ![]() $y_0 \not \in \overline{\Lambda}$, then we can find some constant r > 0 such that
$y_0 \not \in \overline{\Lambda}$, then we can find some constant r > 0 such that  $y_n \in B_{r / 2}(y_0) \subset \overline{\Lambda}^c$. Arguing as before, we can reach a contradiction. So,
$y_n \in B_{r / 2}(y_0) \subset \overline{\Lambda}^c$. Arguing as before, we can reach a contradiction. So, ![]() $y_0 \in \overline{\Lambda}$.
$y_0 \in \overline{\Lambda}$.
It remains to show that ![]() $V(y_0) = V_0$. Arguing by contradiction, again we may assume that
$V(y_0) = V_0$. Arguing by contradiction, again we may assume that ![]() $V(y_0) \gt V_0$. From (4.13), together with Fatou’s lemma and the invariance of
$V(y_0) \gt V_0$. From (4.13), together with Fatou’s lemma and the invariance of ![]() $\mathbb{R}^N$ by translations, it follows that
$\mathbb{R}^N$ by translations, it follows that
 \begin{align*}
c_{V_0} & = I_{V_0}(\hat{v})\\
& \lt \liminf_{n \rightarrow \infty} \Bigg( \frac{1}{p} [\hat{v}_n]_{s,p}^p + \frac{1}{q} [\hat{v}_n]_{s,q}^q + \int_{\mathbb{R}^N} V(\varepsilon_n x + y_n) \left(\frac{1}{p}|\hat{v}_n|^p + \frac{1}{q}|\hat{v}_n|^q\right) dx\\
& - \frac{1}{2}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\hat{v}_n)\right) F(\hat{v}_n) dx\Bigg)\\
& \leqslant \liminf_{n \rightarrow \infty}J_{\varepsilon_n}(t_n u_n) \leqslant \liminf_{n \rightarrow \infty}J_{\varepsilon_n}(u_n) = c_{V_0}.
\end{align*}
\begin{align*}
c_{V_0} & = I_{V_0}(\hat{v})\\
& \lt \liminf_{n \rightarrow \infty} \Bigg( \frac{1}{p} [\hat{v}_n]_{s,p}^p + \frac{1}{q} [\hat{v}_n]_{s,q}^q + \int_{\mathbb{R}^N} V(\varepsilon_n x + y_n) \left(\frac{1}{p}|\hat{v}_n|^p + \frac{1}{q}|\hat{v}_n|^q\right) dx\\
& - \frac{1}{2}\int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * F(\hat{v}_n)\right) F(\hat{v}_n) dx\Bigg)\\
& \leqslant \liminf_{n \rightarrow \infty}J_{\varepsilon_n}(t_n u_n) \leqslant \liminf_{n \rightarrow \infty}J_{\varepsilon_n}(u_n) = c_{V_0}.
\end{align*} This is impossible. So, from hypothesis ![]() $(V_2)$, it follows that
$(V_2)$, it follows that ![]() $y_0 \in M$. This proof is now complete.
$y_0 \in M$. This proof is now complete.
Lemma 4.4. For any ![]() $\delta \gt 0,$ we have
$\delta \gt 0,$ we have
 \begin{align*}\lim_{\varepsilon \rightarrow 0} \sup_{u \in \hat{\mathcal{N}}_\varepsilon} {\mathrm{dist}\,}(\beta_\varepsilon(u),M_\delta) = 0.\end{align*}
\begin{align*}\lim_{\varepsilon \rightarrow 0} \sup_{u \in \hat{\mathcal{N}}_\varepsilon} {\mathrm{dist}\,}(\beta_\varepsilon(u),M_\delta) = 0.\end{align*}Proof. Let ![]() $\varepsilon_n \rightarrow 0$ in
$\varepsilon_n \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$, then we can find a sequence
$n \rightarrow \infty$, then we can find a sequence  $\left\{u_n\right\}_{n \in \mathbb{N}} \subset \hat{\mathcal{N}}_{\varepsilon_n}$ such that
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset \hat{\mathcal{N}}_{\varepsilon_n}$ such that
 \begin{align*}\sup_{u \in \hat{\mathcal{N}}_{\varepsilon_n}} \inf_{y \in M_\delta} |\beta_{\varepsilon_n}(u_n) - y| = \inf_{y \in M_\delta} |\beta_{\varepsilon_n}(u_n) - y| + o_n(1) \ \text{as } n \rightarrow \infty.\end{align*}
\begin{align*}\sup_{u \in \hat{\mathcal{N}}_{\varepsilon_n}} \inf_{y \in M_\delta} |\beta_{\varepsilon_n}(u_n) - y| = \inf_{y \in M_\delta} |\beta_{\varepsilon_n}(u_n) - y| + o_n(1) \ \text{as } n \rightarrow \infty.\end{align*} Noting that  $\left\{u_n\right\}_{n \in \mathbb{N}} \subset \hat{\mathcal{N}}_{\varepsilon_n} \subset \mathcal{N}_{\varepsilon_n}$, we infer that
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset \hat{\mathcal{N}}_{\varepsilon_n} \subset \mathcal{N}_{\varepsilon_n}$, we infer that
and so
 \begin{align*}\lim_{n \rightarrow \infty} J_{\varepsilon_n}(u_n) = c_{V_0}.\end{align*}
\begin{align*}\lim_{n \rightarrow \infty} J_{\varepsilon_n}(u_n) = c_{V_0}.\end{align*} Then, we deduce from lemma 4.3 that for ![]() $n \in \mathbb{N}$ large enough, there exists some sequence
$n \in \mathbb{N}$ large enough, there exists some sequence  $\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that
$\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that ![]() $y_n = \varepsilon_n \hat{y}_n \in M_\delta$. So, we have
$y_n = \varepsilon_n \hat{y}_n \in M_\delta$. So, we have
 \begin{align*}\beta_{\varepsilon_n}(u_n) = y_n + \frac{\int_{\mathbb{R}^N} \left(\zeta(\varepsilon_n z + y_n) - y_n\right) \left(|u_n(z + \hat{y}_n)|^p + |u_n(z + \hat{y}_n)|^q\right) dz}{\int_{\mathbb{R}^N} \left(|u_n(z + \hat{y}_n)|^p + |u_n(z + \hat{y}_n)|^q\right) dz}.\end{align*}
\begin{align*}\beta_{\varepsilon_n}(u_n) = y_n + \frac{\int_{\mathbb{R}^N} \left(\zeta(\varepsilon_n z + y_n) - y_n\right) \left(|u_n(z + \hat{y}_n)|^p + |u_n(z + \hat{y}_n)|^q\right) dz}{\int_{\mathbb{R}^N} \left(|u_n(z + \hat{y}_n)|^p + |u_n(z + \hat{y}_n)|^q\right) dz}.\end{align*} Taking into account the facts that ![]() $\left\{\hat{u}_n(\cdot + \hat{y}_n)\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ has a convergent subsequence and
$\left\{\hat{u}_n(\cdot + \hat{y}_n)\right\}_{n \in \mathbb{N}} \subset {X_{V_0}}$ has a convergent subsequence and ![]() $\varepsilon_n z + y_n \rightarrow y_0 \in M$ as
$\varepsilon_n z + y_n \rightarrow y_0 \in M$ as ![]() $n \rightarrow \infty$, we derive that
$n \rightarrow \infty$, we derive that ![]() $\beta_{\varepsilon_n}(u_n) = y_n + o_n(1)$ in
$\beta_{\varepsilon_n}(u_n) = y_n + o_n(1)$ in ![]() $\mathbb{R}^N$ as
$\mathbb{R}^N$ as ![]() $n \rightarrow \infty$. So, there exists a sequence
$n \rightarrow \infty$. So, there exists a sequence ![]() $\left\{y_n\right\}_{n \in \mathbb{N}} \subset M_\delta$ such that
$\left\{y_n\right\}_{n \in \mathbb{N}} \subset M_\delta$ such that
 \begin{align*}\lim_{n \rightarrow \infty} |\beta_{\varepsilon_n}(u_n) - y_n| = 0.\end{align*}
\begin{align*}\lim_{n \rightarrow \infty} |\beta_{\varepsilon_n}(u_n) - y_n| = 0.\end{align*}This ends the proof of the lemma.
5. Multiple solutions for problem (2.2)
In this section, we shall establish a relationship between the topology of M and the number of solutions for problem (2.2). Since ![]() $\mathcal{N}_\varepsilon$ is not a C 1 submanifold of the space Xɛ, we cannot use directly the standard Ljusternik–Schnirelmann theory, but we can bypass this difficulty by applying the abstract results in the study by Szulkin & Weth [Reference Szulkin, Weth, Gao and Motreanu55].
$\mathcal{N}_\varepsilon$ is not a C 1 submanifold of the space Xɛ, we cannot use directly the standard Ljusternik–Schnirelmann theory, but we can bypass this difficulty by applying the abstract results in the study by Szulkin & Weth [Reference Szulkin, Weth, Gao and Motreanu55].
Theorem 5.1 Let ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq).$ Assume that
$\nu \lt (N - \mu) q / (N - sq).$ Assume that ![]() $(f_1)$–
$(f_1)$–![]() $(f_4)$ and
$(f_4)$ and ![]() $(V_1)$–
$(V_1)$–![]() $(V_2)$ are fulfilled, then for any δ > 0 satisfying
$(V_2)$ are fulfilled, then for any δ > 0 satisfying ![]() $M_\delta \subset \Lambda,$ there exists
$M_\delta \subset \Lambda,$ there exists ![]() $\hat{\varepsilon}_\delta \gt 0$ such that for any
$\hat{\varepsilon}_\delta \gt 0$ such that for any ![]() $\varepsilon \in (0,\hat{\varepsilon}_\delta)$ problem (2.2) possesses at least
$\varepsilon \in (0,\hat{\varepsilon}_\delta)$ problem (2.2) possesses at least ![]() $cat_{M_\delta}(M)$ positive solutions.
$cat_{M_\delta}(M)$ positive solutions.
Proof. For any fixed ɛ > 0, we introduce the mapping ![]() $\alpha_\varepsilon : M \mapsto S_\varepsilon^+$ defined by
$\alpha_\varepsilon : M \mapsto S_\varepsilon^+$ defined by
Consequently, we deduce from lemma 4.1 that
 \begin{align}
\lim_{\varepsilon \rightarrow 0} \psi_\varepsilon(\alpha_\varepsilon(y)) = \lim_{\varepsilon \rightarrow 0} J_\varepsilon(\Phi_\varepsilon(y)) = c_{V_0} \ \text{uniformly in } y \in M.
\end{align}
\begin{align}
\lim_{\varepsilon \rightarrow 0} \psi_\varepsilon(\alpha_\varepsilon(y)) = \lim_{\varepsilon \rightarrow 0} J_\varepsilon(\Phi_\varepsilon(y)) = c_{V_0} \ \text{uniformly in } y \in M.
\end{align}Let us introduce the following function:
 \begin{align*}h'(\varepsilon) : = \sup_{y \in M} |\psi_\varepsilon(\alpha_\varepsilon(y)) - c_{V_0}|.\end{align*}
\begin{align*}h'(\varepsilon) : = \sup_{y \in M} |\psi_\varepsilon(\alpha_\varepsilon(y)) - c_{V_0}|.\end{align*} According to (5.1), we see that ![]() $h'(\varepsilon) \rightarrow 0$ in
$h'(\varepsilon) \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $\varepsilon \rightarrow 0$. Also, we define the following set:
$\varepsilon \rightarrow 0$. Also, we define the following set:
 \begin{align*}\hat{S}_\varepsilon^+ := \left\{\omega \in S_\varepsilon^+ : \psi_\varepsilon(\omega) \leqslant c_{V_0} + h'(\varepsilon)\right\}.\end{align*}
\begin{align*}\hat{S}_\varepsilon^+ := \left\{\omega \in S_\varepsilon^+ : \psi_\varepsilon(\omega) \leqslant c_{V_0} + h'(\varepsilon)\right\}.\end{align*} Clearly, for all ![]() $y \in M$ and ɛ > 0,
$y \in M$ and ɛ > 0, ![]() $\psi_\varepsilon(\alpha_\varepsilon(y)) \in \hat{S}_\varepsilon^+$, and so
$\psi_\varepsilon(\alpha_\varepsilon(y)) \in \hat{S}_\varepsilon^+$, and so ![]() $\hat{S}_\varepsilon^+ \neq \emptyset$.
$\hat{S}_\varepsilon^+ \neq \emptyset$.
From lemma 4.1, lemma 2.2 (c), lemma 4.4, and lemma 4.2, it follows that there exists ![]() $\hat{\varepsilon} = \hat{\varepsilon}_\delta \gt 0$ such that the following diagram is well-defined:
$\hat{\varepsilon} = \hat{\varepsilon}_\delta \gt 0$ such that the following diagram is well-defined:
 \begin{align*}M \stackrel{\Phi_\varepsilon}{\longmapsto} \Phi_\varepsilon(M) \stackrel{m_\varepsilon^{- 1}}{\longmapsto} \alpha_\varepsilon(M) \stackrel{m_\varepsilon}{\longmapsto} \Phi_\varepsilon(M) \stackrel{\beta_\varepsilon}{\longmapsto} M_\delta \ \text{for any } \varepsilon \in (0, \hat{\varepsilon}).\end{align*}
\begin{align*}M \stackrel{\Phi_\varepsilon}{\longmapsto} \Phi_\varepsilon(M) \stackrel{m_\varepsilon^{- 1}}{\longmapsto} \alpha_\varepsilon(M) \stackrel{m_\varepsilon}{\longmapsto} \Phi_\varepsilon(M) \stackrel{\beta_\varepsilon}{\longmapsto} M_\delta \ \text{for any } \varepsilon \in (0, \hat{\varepsilon}).\end{align*} Using lemma 4.2 and decreasing ![]() $\hat{\varepsilon}$ if necessary, for all
$\hat{\varepsilon}$ if necessary, for all ![]() $y \in M$, we have
$y \in M$, we have ![]() $\beta_\varepsilon(\Phi_\varepsilon(y)) = y + l(\varepsilon,y)$, where
$\beta_\varepsilon(\Phi_\varepsilon(y)) = y + l(\varepsilon,y)$, where ![]() $|l(\varepsilon,y)| \leqslant \delta / 2$ uniformly in
$|l(\varepsilon,y)| \leqslant \delta / 2$ uniformly in ![]() $y \in M$ and for all
$y \in M$ and for all ![]() $\varepsilon \in (0,\hat{\varepsilon})$. Hence,
$\varepsilon \in (0,\hat{\varepsilon})$. Hence, ![]() $H(t,y) := y + (1- t) l(\varepsilon,y)$ for
$H(t,y) := y + (1- t) l(\varepsilon,y)$ for ![]() $(t,y) \in [0,1] \times M$ is homotopy between
$(t,y) \in [0,1] \times M$ is homotopy between ![]() $\beta_\varepsilon \circ \Phi_\varepsilon = \left(\beta_\varepsilon \circ m_\varepsilon\right) \circ \left(m_\varepsilon^{- 1} \circ \Phi_\varepsilon\right)$ and the inclusion map
$\beta_\varepsilon \circ \Phi_\varepsilon = \left(\beta_\varepsilon \circ m_\varepsilon\right) \circ \left(m_\varepsilon^{- 1} \circ \Phi_\varepsilon\right)$ and the inclusion map ![]() $id : M \mapsto M_\delta$. This means that
$id : M \mapsto M_\delta$. This means that
Additionally, let us choose a function ![]() $h'(\varepsilon) \gt 0$ such that
$h'(\varepsilon) \gt 0$ such that ![]() $h'(\varepsilon) \rightarrow 0$ in
$h'(\varepsilon) \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $\varepsilon \rightarrow 0$ and such that
$\varepsilon \rightarrow 0$ and such that ![]() $c_{V_0} + h'(\varepsilon)$ is not a critical level for the functional Jɛ. Using corollary 2.9 and theorem 27 in the study by Szulkin and Weth [Reference Szulkin, Weth, Gao and Motreanu55], for ɛ > 0 sufficiently small, we can deduce that ψɛ possesses at least
$c_{V_0} + h'(\varepsilon)$ is not a critical level for the functional Jɛ. Using corollary 2.9 and theorem 27 in the study by Szulkin and Weth [Reference Szulkin, Weth, Gao and Motreanu55], for ɛ > 0 sufficiently small, we can deduce that ψɛ possesses at least ![]() $cat_{\alpha_\varepsilon(M)} \alpha_\varepsilon(M)$ critical points on
$cat_{\alpha_\varepsilon(M)} \alpha_\varepsilon(M)$ critical points on  $\hat{S}_\varepsilon^+$. So, lemma 2.3 and (5.2) imply that the functional Jɛ has at least
$\hat{S}_\varepsilon^+$. So, lemma 2.3 and (5.2) imply that the functional Jɛ has at least ![]() $cat_{M_\delta}(M)$ critical points in
$cat_{M_\delta}(M)$ critical points in ![]() $\hat{\mathcal{N}}_\varepsilon$. This proof is now complete.
$\hat{\mathcal{N}}_\varepsilon$. This proof is now complete.
6. Proof of theorem 1.2
The main idea is to show that the solutions obtained in theorem 5.1 verify the following estimate:
Then, we can deduce from this fact that these solutions are indeed solutions of the original problem (1.3). To this end, we shall treat the regularity of non-negative solutions to problem (2.2). More precisely, we first establish the following result inspired by Moser [Reference Moser48] and Ambrosio and Rădulescu [Reference Ambrosio and Rădulescu11].
Lemma 6.1. Let ![]() $0 \lt \mu \lt sp$ and
$0 \lt \mu \lt sp$ and ![]() $\nu \lt (N - \mu) q / (N - sq)$, and let
$\nu \lt (N - \mu) q / (N - sq)$, and let ![]() $\varepsilon_n \rightarrow 0$ in
$\varepsilon_n \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$ and
$n \rightarrow \infty$ and  $u_n \in \hat{\mathcal{N}}_{\varepsilon_n}$ be a solution to problem (2.2). Then,
$u_n \in \hat{\mathcal{N}}_{\varepsilon_n}$ be a solution to problem (2.2). Then, ![]() $J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in
$J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty,$ and there exists a sequence
$n \rightarrow \infty,$ and there exists a sequence  $\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that
$\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that ![]() $\hat{u}_n(\cdot) := u_n(\cdot + \hat{y}_n) \in L^\infty(\mathbb{R}^N)$ and
$\hat{u}_n(\cdot) := u_n(\cdot + \hat{y}_n) \in L^\infty(\mathbb{R}^N)$ and  $|\hat{u}_n|_{L^\infty(\mathbb{R}^N)} \leqslant C$ for all
$|\hat{u}_n|_{L^\infty(\mathbb{R}^N)} \leqslant C$ for all ![]() $n \in \mathbb{N},$ for some constant C > 0. Furthermore,
$n \in \mathbb{N},$ for some constant C > 0. Furthermore,
Proof. On account of the fact that  $u_n \in \hat{\mathcal{N}}_{\varepsilon_n}$, arguing as in the proof of lemma 4.4, we see that
$u_n \in \hat{\mathcal{N}}_{\varepsilon_n}$, arguing as in the proof of lemma 4.4, we see that ![]() $J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in
$J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$. Then, from lemma 4.3, it follows that there exists a sequence
$n \rightarrow \infty$. Then, from lemma 4.3, it follows that there exists a sequence  $\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that
$\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that ![]() $\hat{u}_n(\cdot) := u_n(\cdot + \hat{y}_n) \rightarrow \hat{u}(\cdot) \in {X_{V_0}}$ and
$\hat{u}_n(\cdot) := u_n(\cdot + \hat{y}_n) \rightarrow \hat{u}(\cdot) \in {X_{V_0}}$ and ![]() $y_n :=\varepsilon_n \hat{y}_n \rightarrow y_0 \in M$ as
$y_n :=\varepsilon_n \hat{y}_n \rightarrow y_0 \in M$ as ![]() $n \rightarrow \infty$. For any L > 0 and β > 1, we introduce the function
$n \rightarrow \infty$. For any L > 0 and β > 1, we introduce the function
 \begin{align*}\psi(\hat{u}_n) := \hat{u}_n \hat{u}_{n,L}^{q (\beta - 1)} \in X_{\varepsilon_n}, \ \text{where } \hat{u}_{n, L} := \min\left\{\hat{u}_n,L\right\}.\end{align*}
\begin{align*}\psi(\hat{u}_n) := \hat{u}_n \hat{u}_{n,L}^{q (\beta - 1)} \in X_{\varepsilon_n}, \ \text{where } \hat{u}_{n, L} := \min\left\{\hat{u}_n,L\right\}.\end{align*} Taking ![]() $\psi(\hat{u}_n)$ as test function, we have
$\psi(\hat{u}_n)$ as test function, we have
 \begin{align*}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\hat{u}_n(x) - \hat{u}_n(y)|^{p - 2}(\hat{u}_n(x) - \hat{u}_n(y))(\psi(\hat{u}_n(x)) - \psi(\hat{u}_n(y)))}{|x - y|^{N + sp}} dxdy\\
+ \ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\hat{u}_n(x) - \hat{u}_n(y)|^{q - 2}(\hat{u}_n(x) - \hat{u}_n(y))(\psi(\hat{u}_n(x)) - \psi(\hat{u}_n(y)))}{|x - y|^{N + sq}} dxdy\\
+ \ & \int_{\mathbb{R}^N} V(\varepsilon_n x + y_n) |\hat{u}_n|^{p - 2} \hat{u}_n \psi(\hat{u}_n) dx + \int_{\mathbb{R}^N} V(\varepsilon_n x + y_n) |\hat{u}_n|^{q - 2} \hat{u}_n \psi(\hat{u}_n) dx\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon_n x + y_n, \hat{u}_n)\right) g(\varepsilon_n x + y_n,\hat{u}_n) \psi(\hat{u}_n) dx.
\end{align*}
\begin{align*}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\hat{u}_n(x) - \hat{u}_n(y)|^{p - 2}(\hat{u}_n(x) - \hat{u}_n(y))(\psi(\hat{u}_n(x)) - \psi(\hat{u}_n(y)))}{|x - y|^{N + sp}} dxdy\\
+ \ & \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\hat{u}_n(x) - \hat{u}_n(y)|^{q - 2}(\hat{u}_n(x) - \hat{u}_n(y))(\psi(\hat{u}_n(x)) - \psi(\hat{u}_n(y)))}{|x - y|^{N + sq}} dxdy\\
+ \ & \int_{\mathbb{R}^N} V(\varepsilon_n x + y_n) |\hat{u}_n|^{p - 2} \hat{u}_n \psi(\hat{u}_n) dx + \int_{\mathbb{R}^N} V(\varepsilon_n x + y_n) |\hat{u}_n|^{q - 2} \hat{u}_n \psi(\hat{u}_n) dx\\
=\ & \int_{\mathbb{R}^N} \left(\frac{1}{|x|^\mu} * G(\varepsilon_n x + y_n, \hat{u}_n)\right) g(\varepsilon_n x + y_n,\hat{u}_n) \psi(\hat{u}_n) dx.
\end{align*} Additionally, applying the boundedness of the sequence ![]() $\left\{\hat{u}_n\right\}_{n \in \mathbb{N}} \subset X_{\varepsilon_n}$ and arguing as in the proof of lemma 2.6, we can deduce that there exists
$\left\{\hat{u}_n\right\}_{n \in \mathbb{N}} \subset X_{\varepsilon_n}$ and arguing as in the proof of lemma 2.6, we can deduce that there exists ![]() $C_0 \gt 0$ such that
$C_0 \gt 0$ such that
 \begin{align*}\sup_{n \in \mathbb{N}} \left|\frac{1}{|x|^\mu} * G(\varepsilon_n x + y_n, \hat{u}_n)\right|_{L^\infty(\mathbb{R}^N)} \leqslant C_0.\end{align*}
\begin{align*}\sup_{n \in \mathbb{N}} \left|\frac{1}{|x|^\mu} * G(\varepsilon_n x + y_n, \hat{u}_n)\right|_{L^\infty(\mathbb{R}^N)} \leqslant C_0.\end{align*} According to the hypotheses on g, we see that for any σ > 0 there exists ![]() $C_\sigma \gt 0$ such that
$C_\sigma \gt 0$ such that
 \begin{align*}|g(x,t)| \leqslant \sigma |t|^{p - 1} + C_\sigma |t|^{q_s^* - 1} \ \text{for all } (x,t) \in \mathbb{R}^N \times \mathbb{R}.\end{align*}
\begin{align*}|g(x,t)| \leqslant \sigma |t|^{p - 1} + C_\sigma |t|^{q_s^* - 1} \ \text{for all } (x,t) \in \mathbb{R}^N \times \mathbb{R}.\end{align*} Choosing ![]() $\sigma \in (0,V_0/{C_0})$, together with the above inequalities, we can infer that
$\sigma \in (0,V_0/{C_0})$, together with the above inequalities, we can infer that
 \begin{align}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\hat{u}_n(x) - \hat{u}_n(y)|^{p - 2}(\hat{u}_n(x) - \hat{u}_n(y))(\psi(\hat{u}_n(x)) - \psi(\hat{u}_n(y)))}{|x - y|^{N + sp}} dxdy \nonumber\\
& + \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\hat{u}_n(x) - \hat{u}_n(y)|^{q - 2}(\hat{u}_n(x) - \hat{u}_n(y))(\psi(\hat{u}_n(x)) - \psi(\hat{u}_n(y)))}{|x - y|^{N + sq}} dxdy\nonumber\\
\leqslant \ & C \int_{\mathbb{R}^N} |\hat{u}_n|^{q_s^*}\hat{u}_{n,L}^{q (\beta - 1)} dx
\end{align}
\begin{align}
& \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\hat{u}_n(x) - \hat{u}_n(y)|^{p - 2}(\hat{u}_n(x) - \hat{u}_n(y))(\psi(\hat{u}_n(x)) - \psi(\hat{u}_n(y)))}{|x - y|^{N + sp}} dxdy \nonumber\\
& + \int_{\mathbb{R}^N}\int_{\mathbb{R}^N} \frac{|\hat{u}_n(x) - \hat{u}_n(y)|^{q - 2}(\hat{u}_n(x) - \hat{u}_n(y))(\psi(\hat{u}_n(x)) - \psi(\hat{u}_n(y)))}{|x - y|^{N + sq}} dxdy\nonumber\\
\leqslant \ & C \int_{\mathbb{R}^N} |\hat{u}_n|^{q_s^*}\hat{u}_{n,L}^{q (\beta - 1)} dx
\end{align}for some constant C > 0.
Let us define the following functions:
 \begin{align*}\varphi(t) := \frac{|t|^q}{q} \quad \ \text{and } \quad\Upsilon(t) := \int^t_0 (\psi'
(\tau))^{\frac{1}{q}} d\tau.\end{align*}
\begin{align*}\varphi(t) := \frac{|t|^q}{q} \quad \ \text{and } \quad\Upsilon(t) := \int^t_0 (\psi'
(\tau))^{\frac{1}{q}} d\tau.\end{align*}We first observe that ψ is an increasing function, and hence
Then, we can infer from (6.3) and the Jensen inequality that
We also point out that
 \begin{align}
\Upsilon(\hat{u}_n) \geqslant \frac{1}{\beta} \hat{u}_n \hat{u}_{n,L}^{\beta - 1}.
\end{align}
\begin{align}
\Upsilon(\hat{u}_n) \geqslant \frac{1}{\beta} \hat{u}_n \hat{u}_{n,L}^{\beta - 1}.
\end{align}So, putting together with (6.2), (6.3), (6.4), and (6.5) and using the Sobolev embedding, we infer that there exists some constant C > 0 such that
 \begin{align}
|\hat{u}_n \hat{u}_{n,L}^{\beta - 1}|_{q_s^*}^q \leqslant C \beta^q \int_{\mathbb{R}^N} \hat{u}_n^{q_s^*}\hat{u}_{n,L}^{q(\beta - 1)} dx.
\end{align}
\begin{align}
|\hat{u}_n \hat{u}_{n,L}^{\beta - 1}|_{q_s^*}^q \leqslant C \beta^q \int_{\mathbb{R}^N} \hat{u}_n^{q_s^*}\hat{u}_{n,L}^{q(\beta - 1)} dx.
\end{align} Choose  $\beta = \frac{q_s^*}{q}$, and let R > 0 large enough. Combining
$\beta = \frac{q_s^*}{q}$, and let R > 0 large enough. Combining ![]() $\hat{u}_n \rightarrow \hat{u}$ in
$\hat{u}_n \rightarrow \hat{u}$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$ with the Hölder inequality, we can conclude that there exists some constant C > 0 such that
$n \rightarrow \infty$ with the Hölder inequality, we can conclude that there exists some constant C > 0 such that
 \begin{align*}\left(\int_{\mathbb{R}^N} \left(\hat{u}_n \hat{u}_{n,L}^{\frac{q_s^* - q}{q}}\right)^{q_s^*} dx\right)^{\frac{q}{q_s^*}} & \leqslant C \beta^q \int_{\mathbb{R}^N} R^{q_s^* - q} \hat{u}_n^{q_s^*} dx \\
& \quad + C \epsilon \left(\int_{\mathbb{R}^N} \left(\hat{u}_n \hat{u}_{n,L}^{\frac{q_s^* - q}{q}}\right)^{q_s^*} dx\right)^{\frac{q}{q_s^*}}.\end{align*}
\begin{align*}\left(\int_{\mathbb{R}^N} \left(\hat{u}_n \hat{u}_{n,L}^{\frac{q_s^* - q}{q}}\right)^{q_s^*} dx\right)^{\frac{q}{q_s^*}} & \leqslant C \beta^q \int_{\mathbb{R}^N} R^{q_s^* - q} \hat{u}_n^{q_s^*} dx \\
& \quad + C \epsilon \left(\int_{\mathbb{R}^N} \left(\hat{u}_n \hat{u}_{n,L}^{\frac{q_s^* - q}{q}}\right)^{q_s^*} dx\right)^{\frac{q}{q_s^*}}.\end{align*} Then, we choose a fixed ![]() $\epsilon \in (0,1 / C)$ and infer that
$\epsilon \in (0,1 / C)$ and infer that
 \begin{align*}\left(\int_{\mathbb{R}^N} \left(\hat{u}_n \hat{u}_{n,L}^{\frac{q_s^* - q}{q}}\right)^{q_s^*} dx\right)^{\frac{q}{q_s^*}} \leqslant C \beta^q \int R^{q_s^* - q} \hat{u}_n^{q_s^*} dx \lt + \infty.\end{align*}
\begin{align*}\left(\int_{\mathbb{R}^N} \left(\hat{u}_n \hat{u}_{n,L}^{\frac{q_s^* - q}{q}}\right)^{q_s^*} dx\right)^{\frac{q}{q_s^*}} \leqslant C \beta^q \int R^{q_s^* - q} \hat{u}_n^{q_s^*} dx \lt + \infty.\end{align*} In the above inequality, we pass to the limit as ![]() $L \rightarrow + \infty$ and we obtain
$L \rightarrow + \infty$ and we obtain  $\hat{u}_n \in L^{\frac{{q_s^*}^2}{q}}(\mathbb{R}^N)$.
$\hat{u}_n \in L^{\frac{{q_s^*}^2}{q}}(\mathbb{R}^N)$.
Thanks to ![]() $0 \leqslant \hat{u}_{n,L} \leqslant \hat{u}_n$, then in (6.6), we pass to the limit as
$0 \leqslant \hat{u}_{n,L} \leqslant \hat{u}_n$, then in (6.6), we pass to the limit as ![]() $L \rightarrow + \infty$ and we have
$L \rightarrow + \infty$ and we have
 \begin{align*}|\hat{u}_n|_{\beta q_s^*}^{\beta q} \leqslant C \beta^q \int_{\mathbb{R}^N} \hat{u}_n^{q_s^* + q(\beta - 1)} dx.\end{align*}
\begin{align*}|\hat{u}_n|_{\beta q_s^*}^{\beta q} \leqslant C \beta^q \int_{\mathbb{R}^N} \hat{u}_n^{q_s^* + q(\beta - 1)} dx.\end{align*}This means that
 \begin{align*}\left(\int_{\mathbb{R}^N} \hat{u}_n^{\beta q_s^*} dx\right)^{\frac{1}{q_s^*(\beta - 1)}} \leqslant (C^{1 / q} \beta)^{\frac{1}{\beta - 1}} \left(\int_{\mathbb{R}^N} \hat{u}_n^{q_s^* + q(\beta - 1)} dx\right)^{\frac{1}{q(\beta - 1)}}.\end{align*}
\begin{align*}\left(\int_{\mathbb{R}^N} \hat{u}_n^{\beta q_s^*} dx\right)^{\frac{1}{q_s^*(\beta - 1)}} \leqslant (C^{1 / q} \beta)^{\frac{1}{\beta - 1}} \left(\int_{\mathbb{R}^N} \hat{u}_n^{q_s^* + q(\beta - 1)} dx\right)^{\frac{1}{q(\beta - 1)}}.\end{align*} For ![]() $1 \leqslant m \in \mathbb{N}$, let us define
$1 \leqslant m \in \mathbb{N}$, let us define
 \begin{align*}q_s^* + q(\beta_{m + 1} - 1) = \beta_m q_s^*\quad \ \text{and } \quad \beta_1 = \frac{q_s^*}{q}.\end{align*}
\begin{align*}q_s^* + q(\beta_{m + 1} - 1) = \beta_m q_s^*\quad \ \text{and } \quad \beta_1 = \frac{q_s^*}{q}.\end{align*}It follows that
and so
 \begin{align*}\lim_{m \rightarrow \infty} \beta_m = + \infty.\end{align*}
\begin{align*}\lim_{m \rightarrow \infty} \beta_m = + \infty.\end{align*}Let us define
 \begin{align*}T_m : =\left(\int_{\mathbb{R}^N} \hat{u}_n^{\beta_m q_s^*} dx\right)^{\frac{1}{q_s^*(\beta_m - 1)}}.\end{align*}
\begin{align*}T_m : =\left(\int_{\mathbb{R}^N} \hat{u}_n^{\beta_m q_s^*} dx\right)^{\frac{1}{q_s^*(\beta_m - 1)}}.\end{align*}Then, we have
 \begin{align*}T_{m + 1} \leqslant (C^{1 / q} \beta_{m + 1})^{\frac{1}{\beta_{m + 1} - 1}} T_m.\end{align*}
\begin{align*}T_{m + 1} \leqslant (C^{1 / q} \beta_{m + 1})^{\frac{1}{\beta_{m + 1} - 1}} T_m.\end{align*}Consequently, using a standard iteration argument, we have
 \begin{align*}T_{m+1} \leqslant \prod_{k=1}^m(C^{1 / q} \beta_{k + 1})^{\frac{1}{\beta_{k + 1} - 1}} T_1 \leqslant \overline{C} T_1, \ \text{where } \overline{C} \ \text{is independent of } m.\end{align*}
\begin{align*}T_{m+1} \leqslant \prod_{k=1}^m(C^{1 / q} \beta_{k + 1})^{\frac{1}{\beta_{k + 1} - 1}} T_1 \leqslant \overline{C} T_1, \ \text{where } \overline{C} \ \text{is independent of } m.\end{align*} In the above inequality, we pass to the limit as ![]() $m \rightarrow \infty$ and then we infer that
$m \rightarrow \infty$ and then we infer that  $|\hat{u}_n|_{L^\infty(\mathbb{R}^N)} \leqslant C$ uniformly in
$|\hat{u}_n|_{L^\infty(\mathbb{R}^N)} \leqslant C$ uniformly in ![]() $n \in \mathbb{N}$.
$n \in \mathbb{N}$.
Next, let us define
 \begin{align*}\kappa_n := - V(\varepsilon_n x + y_n)\left(\hat{u}_n^{p - 1} + \hat{u}_n^{q - 1}\right) + \left(\frac{1}{|x|^\mu} * G(\varepsilon_n x + y_n,\hat{u}_n)\right) g(\varepsilon_n x + y_n,\hat{u}_n).\end{align*}
\begin{align*}\kappa_n := - V(\varepsilon_n x + y_n)\left(\hat{u}_n^{p - 1} + \hat{u}_n^{q - 1}\right) + \left(\frac{1}{|x|^\mu} * G(\varepsilon_n x + y_n,\hat{u}_n)\right) g(\varepsilon_n x + y_n,\hat{u}_n).\end{align*} We point out that ![]() $\hat{u}_n$ satisfies the following equation:
$\hat{u}_n$ satisfies the following equation:
 \begin{align*}(- \Delta)_p^s \hat{u}_n + (- \Delta)_q^s \hat{u}_n = \kappa_n \quad\ \text{in } \mathbb{R}^N.\end{align*}
\begin{align*}(- \Delta)_p^s \hat{u}_n + (- \Delta)_q^s \hat{u}_n = \kappa_n \quad\ \text{in } \mathbb{R}^N.\end{align*} From the growth hypotheses on g, corollary 2.1 in the study by Ambrosio & Rădulescu [Reference Ambrosio and Rădulescu11], ![]() $\hat{u}_n \rightarrow \hat{u}$ in
$\hat{u}_n \rightarrow \hat{u}$ in ![]() ${X_{V_0}}$ as
${X_{V_0}}$ as ![]() $n \rightarrow \infty$, and the uniformly boundedness of the sequence
$n \rightarrow \infty$, and the uniformly boundedness of the sequence ![]() $\left\{\hat{u}_n\right\}_{n \in \mathbb{N}}$ in
$\left\{\hat{u}_n\right\}_{n \in \mathbb{N}}$ in  $L^\infty(\mathbb{R}^N) \cap {X_{V_0}}$, we can conclude that
$L^\infty(\mathbb{R}^N) \cap {X_{V_0}}$, we can conclude that ![]() $\hat{u}_n(x) \rightarrow 0$ in
$\hat{u}_n(x) \rightarrow 0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $|x| \rightarrow +\infty$ uniformly with respect to
$|x| \rightarrow +\infty$ uniformly with respect to ![]() $n \in \mathbb{N}$. This ends the proof of the lemma.
$n \in \mathbb{N}$. This ends the proof of the lemma.
Proof of theorem 1.2 completed
We first choose δ > 0 small enough such that ![]() $M_\delta \subset \Lambda$. Then, we claim that there exists
$M_\delta \subset \Lambda$. Then, we claim that there exists ![]() $\bar{\varepsilon}_\delta \gt 0$ such that for any
$\bar{\varepsilon}_\delta \gt 0$ such that for any ![]() $\varepsilon \in (0,\bar{\varepsilon}_\delta)$ and any solution
$\varepsilon \in (0,\bar{\varepsilon}_\delta)$ and any solution ![]() $u_\varepsilon \in \hat{\mathcal{N}}_\varepsilon$ of problem (2.2), we have
$u_\varepsilon \in \hat{\mathcal{N}}_\varepsilon$ of problem (2.2), we have
Otherwise, we may assume that there exists a subsequence ![]() $\left\{\varepsilon_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}$ such that
$\left\{\varepsilon_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}$ such that ![]() $\varepsilon_n \rightarrow 0$ as
$\varepsilon_n \rightarrow 0$ as ![]() $n \rightarrow \infty$,
$n \rightarrow \infty$,  $u_{\varepsilon_n} \in \hat{\mathcal{N}}_{\varepsilon_n}$ such that
$u_{\varepsilon_n} \in \hat{\mathcal{N}}_{\varepsilon_n}$ such that ![]() $J_{\varepsilon_n}'(u_{\varepsilon_n})=0$ and
$J_{\varepsilon_n}'(u_{\varepsilon_n})=0$ and
 \begin{align}
|u_{\varepsilon_n}|_{L^\infty(\Lambda_{\varepsilon_n}^c)} \geqslant a.
\end{align}
\begin{align}
|u_{\varepsilon_n}|_{L^\infty(\Lambda_{\varepsilon_n}^c)} \geqslant a.
\end{align} But we see that ![]() $J_{\varepsilon_n}(u_{\varepsilon_n}) \rightarrow c_{V_0}$ in
$J_{\varepsilon_n}(u_{\varepsilon_n}) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$. Thus, from lemma 4.3, it follows that there exists a sequence
$n \rightarrow \infty$. Thus, from lemma 4.3, it follows that there exists a sequence  $\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that
$\left\{\hat{y}_n\right\}_{n \in \mathbb{N}} \subset \mathbb{R}^N$ such that ![]() $\hat{u}_n(\cdot) :=u_{\varepsilon_n}(\cdot + \hat{y}_n) \rightarrow \hat{u}(\cdot)$ in
$\hat{u}_n(\cdot) :=u_{\varepsilon_n}(\cdot + \hat{y}_n) \rightarrow \hat{u}(\cdot)$ in ![]() ${X_{V_0}}$ and
${X_{V_0}}$ and ![]() $\varepsilon_n \hat{y}_n \rightarrow y_0 \in M$ as
$\varepsilon_n \hat{y}_n \rightarrow y_0 \in M$ as ![]() $n \rightarrow \infty$.
$n \rightarrow \infty$.
Next, we choose r > 0 such that ![]() $B_r(y_0) \subset B_{2r}(y_0) \subset \Lambda$, and so
$B_r(y_0) \subset B_{2r}(y_0) \subset \Lambda$, and so  $B_{\frac{r}{\varepsilon_n}}\left(\frac{y_0}{\varepsilon_n}\right) \subset \Lambda_{\varepsilon_n}$. Furthermore, for n large enough, we can deduce that
$B_{\frac{r}{\varepsilon_n}}\left(\frac{y_0}{\varepsilon_n}\right) \subset \Lambda_{\varepsilon_n}$. Furthermore, for n large enough, we can deduce that  $\Lambda_{\varepsilon_n}^c \subset B_{\frac{r}{\varepsilon_n}}^c(\hat{y}_n)$. In addition, from (6.1), we see that
$\Lambda_{\varepsilon_n}^c \subset B_{\frac{r}{\varepsilon_n}}^c(\hat{y}_n)$. In addition, from (6.1), we see that ![]() $\hat{u}_n(x) \rightarrow 0$ as
$\hat{u}_n(x) \rightarrow 0$ as ![]() $|x| \rightarrow + \infty$ uniformly in
$|x| \rightarrow + \infty$ uniformly in ![]() $n \in \mathbb{N}$. Therefore, we can find R > 0 such that
$n \in \mathbb{N}$. Therefore, we can find R > 0 such that ![]() $\hat{u}_n(x) \lt a$ for any
$\hat{u}_n(x) \lt a$ for any ![]() $|x| \geqslant R$,
$|x| \geqslant R$, ![]() $n \in \mathbb{N}$. Consequently,
$n \in \mathbb{N}$. Consequently, ![]() $u_{\varepsilon_n}(x) \lt a$ for any
$u_{\varepsilon_n}(x) \lt a$ for any ![]() $x \in B_R^c(\hat{y}_n)$,
$x \in B_R^c(\hat{y}_n)$, ![]() $n \in \mathbb{N}$. Moreover, for
$n \in \mathbb{N}$. Moreover, for ![]() $n \in \mathbb{N}$ sufficiently large, we know that
$n \in \mathbb{N}$ sufficiently large, we know that
 \begin{align*}\Lambda_{\varepsilon_n}^c \subset B_{\frac{r}{\varepsilon_n}}^c(\hat{y}_n) \subset B_R^c(\hat{y}_n).\end{align*}
\begin{align*}\Lambda_{\varepsilon_n}^c \subset B_{\frac{r}{\varepsilon_n}}^c(\hat{y}_n) \subset B_R^c(\hat{y}_n).\end{align*} Thus, we infer that ![]() $u_{\varepsilon_n}(x) \lt a$ for any
$u_{\varepsilon_n}(x) \lt a$ for any ![]() $x \in \Lambda_{\varepsilon_n}^c$ and for all
$x \in \Lambda_{\varepsilon_n}^c$ and for all ![]() $n \in \mathbb{N}$ large enough, which contradicts relation (6.8).
$n \in \mathbb{N}$ large enough, which contradicts relation (6.8).
Fix ![]() $\varepsilon \in (0,\varepsilon_\delta)$, where
$\varepsilon \in (0,\varepsilon_\delta)$, where ![]() $\varepsilon_\delta := \min\{\hat{\varepsilon}_\delta, \bar{\varepsilon}_\delta\}$. From theorem 5.1, we can see that problem (2.2) has at least
$\varepsilon_\delta := \min\{\hat{\varepsilon}_\delta, \bar{\varepsilon}_\delta\}$. From theorem 5.1, we can see that problem (2.2) has at least ![]() $\text{cat}_{M_\delta}(M)$ nontrivial solutions. Now, we use uɛ to denote one of these solutions, and so
$\text{cat}_{M_\delta}(M)$ nontrivial solutions. Now, we use uɛ to denote one of these solutions, and so ![]() $u_\varepsilon \in \hat{\mathcal{N}}_\varepsilon$. Then, using (6.7) and recalling that the definitions of g and G, we can also infer that uɛ is a solution of problem (1.3). So, problem (1.3) possesses at least
$u_\varepsilon \in \hat{\mathcal{N}}_\varepsilon$. Then, using (6.7) and recalling that the definitions of g and G, we can also infer that uɛ is a solution of problem (1.3). So, problem (1.3) possesses at least ![]() $\text{cat}_{M_\delta}(M)$ nontrivial solutions.
$\text{cat}_{M_\delta}(M)$ nontrivial solutions.
Finally, we establish the behaviour of the maximum points of solutions to problem (1.3). Let us choose ![]() $\varepsilon_n \rightarrow 0$ and consider a sequence
$\varepsilon_n \rightarrow 0$ and consider a sequence ![]() $\left\{u_n\right\}_{n \in \mathbb{N}} \subset X_{\varepsilon_n}$ of solutions for problem (1.3) as before. From
$\left\{u_n\right\}_{n \in \mathbb{N}} \subset X_{\varepsilon_n}$ of solutions for problem (1.3) as before. From ![]() $(g_1)$, it follows that there exists a positive constant
$(g_1)$, it follows that there exists a positive constant ![]() $\iota \lt a$ such that
$\iota \lt a$ such that
 \begin{align}
g(\varepsilon x,t) t \leqslant \frac{V_0}{K}\left(t^p + t^q\right) \ \text{for any } x \in \mathbb{R}^N,\ t \in [0,\iota],
\end{align}
\begin{align}
g(\varepsilon x,t) t \leqslant \frac{V_0}{K}\left(t^p + t^q\right) \ \text{for any } x \in \mathbb{R}^N,\ t \in [0,\iota],
\end{align} since ![]() $u_n \in \mathcal{N}_{\varepsilon_n}$ and
$u_n \in \mathcal{N}_{\varepsilon_n}$ and ![]() $J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in
$J_{\varepsilon_n}(u_n) \rightarrow c_{V_0}$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$. Then, for
$n \rightarrow \infty$. Then, for ![]() $n \in \mathbb{N}$ sufficiently large, we have that
$n \in \mathbb{N}$ sufficiently large, we have that ![]() $u_n \in \mathcal{B}$. Consequently, from lemma 2.6, it follows that
$u_n \in \mathcal{B}$. Consequently, from lemma 2.6, it follows that
 \begin{align}
\left|\frac{1}{|x|^\mu} * G(\varepsilon_n x, u_n)\right|_{L^\infty(\mathbb{R}^N)} \lt \frac{K}{2} \ \text{for } n \in \mathbb{N} \ \text{large enough}.
\end{align}
\begin{align}
\left|\frac{1}{|x|^\mu} * G(\varepsilon_n x, u_n)\right|_{L^\infty(\mathbb{R}^N)} \lt \frac{K}{2} \ \text{for } n \in \mathbb{N} \ \text{large enough}.
\end{align}Arguing as before, there exists R > 0 such that
 \begin{align}
|u_n|_{L^\infty(B_R^c(\hat{y}_n))} \lt \iota.
\end{align}
\begin{align}
|u_n|_{L^\infty(B_R^c(\hat{y}_n))} \lt \iota.
\end{align}Furthermore, up to a subsequence, we may assume that
Otherwise, if relation (6.12) does not hold, we deduce from (6.11) that  $|u_n|_{L^\infty(\mathbb{R}^N)} \lt \iota$. Using
$|u_n|_{L^\infty(\mathbb{R}^N)} \lt \iota$. Using ![]() $u_n \in \mathcal{N}_{\varepsilon_n}$ again and (6.9)–(6.10), we have
$u_n \in \mathcal{N}_{\varepsilon_n}$ again and (6.9)–(6.10), we have
 \begin{align*}
\|u_n\|_{V_{\varepsilon_n},p}^p + \|u_n\|_{V_{\varepsilon_n},q}^q &\leqslant \int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * G(\varepsilon_n x,u_n)\right) g(\varepsilon_n x, u_n) u_n dx,\\
& \leqslant \frac{V_0}{2} \int_{\mathbb{R}^N} \left(|u_n|^p + |u_n|^q\right) dx\ \ \text{for all } n \in \mathbb{N} \ \text{large enough}.
\end{align*}
\begin{align*}
\|u_n\|_{V_{\varepsilon_n},p}^p + \|u_n\|_{V_{\varepsilon_n},q}^q &\leqslant \int_{\mathbb{R}^N}\left(\frac{1}{|x|^\mu} * G(\varepsilon_n x,u_n)\right) g(\varepsilon_n x, u_n) u_n dx,\\
& \leqslant \frac{V_0}{2} \int_{\mathbb{R}^N} \left(|u_n|^p + |u_n|^q\right) dx\ \ \text{for all } n \in \mathbb{N} \ \text{large enough}.
\end{align*} This implies that ![]() $\|u_n\|_{X_{\varepsilon_n}} = 0$ for all
$\|u_n\|_{X_{\varepsilon_n}} = 0$ for all ![]() $n \in \mathbb{N}$ sufficiently large, which is a contradiction. Consequently, relation (6.12) holds true. On account of (6.11) and (6.12), we can infer that if pn is a global maximum point of un and
$n \in \mathbb{N}$ sufficiently large, which is a contradiction. Consequently, relation (6.12) holds true. On account of (6.11) and (6.12), we can infer that if pn is a global maximum point of un and ![]() $p_n = \hat{y}_n + q_n$ for some
$p_n = \hat{y}_n + q_n$ for some ![]() $q_n \in B_R$,
$q_n \in B_R$, ![]() $\varepsilon_n p_n \rightarrow y_0 \in M$ as
$\varepsilon_n p_n \rightarrow y_0 \in M$ as ![]() $n \rightarrow \infty$; then using the continuity of the potential V we see that
$n \rightarrow \infty$; then using the continuity of the potential V we see that ![]() $V(\varepsilon_n p_n) \rightarrow V(y_0) = V_0$ in
$V(\varepsilon_n p_n) \rightarrow V(y_0) = V_0$ in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n \rightarrow \infty$.
$n \rightarrow \infty$.
This proof is nowcomplete. ![]() $\square$
$\square$
Declarations
Conflict of interest
The authors declare that they have no competing interests.
Data availability
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
Funding
The research of V.D. Rădulescu was supported by the grant ‘Nonlinear Differential Systems in Applied Sciences’ of the Romanian Ministry of Research, Innovation and Digitalization, within PNRR-III-C9-2022-I8/22. This research was partially supported by the Scientific Research Fund of Hunan Provincial Education Department (No. 20B243), the National Natural Science Foundation of China (Nos. 12301219 and 12171486), the Science and Technology Innovation Program of Hunan Province (No. 2024RC3021), the Project for Young Backbone Teachers of Hunan Province (No.10900-150220002), and the Natural Science Foundation for Excellent Young Scholars of Hunan Province (No. 2023JJ20057).