Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-17T05:38:40.963Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact boundedness in periodic functional differential equations with infinite delay

Published online by Cambridge University Press:  14 November 2011

Junji Kato
Junji Kato
Affiliation:
Mathematical Institute, Tohoku University, Sendai 980, Japan
Get access Rights & Permissions [Opens in a new window]

Synopsis

It is the aim of this article to consider some problems arising from the non local-compactness of the phase space for functional differential equations. The compact boundedness, that is, the boundedness depending on each compact set involving the initial values, is proved to be implied from the ultimate boundedness for periodic systems of functional differential equations on Cγ: = {φ ∊ C((–∞,0]) 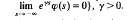Note that it is known that the compactness cannot be dropped in the above. An example is also given to show that the asymptotic stability is not necessarily uniform even for periodic functional differential equations on Co.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 114 , Issue 3-4 , 1990 , pp. 291 - 297
Copyright
Copyright © Royal Society of Edinburgh 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Hale, J. K.. Theory of Functional Differential Equations, Applied Mathematical Sciences 3 (Berlin: Springer, 1977).CrossRefGoogle Scholar
2Hale, J. K. and Kato, J.. Phase space for retarded equation with infinite delay. Funkcial. Ekvac. 21 (1978), 11–41.Google Scholar
3Kato, J., An autonomous system whose solutions are uniformly ultimately bounded but not uniformly bounded. Tohoku Math. J. 32 (1980), 499–504.CrossRefGoogle Scholar
4Kato, J.. Boundedness in functional differential equations. The United States–Japan Seminar on Finite and Infinite Dimensional Dynamical Systems at Kyoto, Japan, 16–21 July, 1989.Google Scholar
5Yoshizawa, T.. Stability Theory and the Existence of Periodic Solutionsand Almost Periodic Solutions, Applied Mathematical Sciences 14, (Berlin: Springer, 1975).CrossRefGoogle Scholar