Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-04T18:01:34.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic stability of spatial homogeneity in a haptotaxis model for oncolytic virotherapy

Part of: Equations of mathematical physics and other areas of application Parabolic equations and systems Physiological, cellular and medical topics Partial differential equations

Published online by Cambridge University Press:  08 January 2021

Youshan Tao  and
Michael Winkler
Youshan Tao
Affiliation:
School of Mathematical Sciences, Shanghai Jiao Tong University, Shanghai200240, P.R. China ([email protected])
Michael Winkler
Affiliation:
Institut für Mathematik, Universität Paderborn, Paderborn, 33098, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

This study considers a model for oncolytic virotherapy, as given by the reaction–diffusion–taxis system

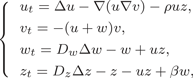\[\begin{eqnarray*} \left\{ \begin{array}{l} u_t = \Delta u - \nabla (u\nabla v)-\rho uz, \\ v_t = - (u+w)v, \\ w_t = D_w \Delta w - w + uz, \\ z_t = D_z \Delta z - z - uz + \beta w, \end{array} \right. \end{eqnarray*}\]
in a smoothly bounded domain Ω ⊂ ℝ2, with parameters Dw > 0, Dz > 0, β > 0 and ρ ⩾ 0.

Previous analysis has asserted that for all reasonably regular initial data, an associated no-flux type initial-boundary value problem admits a global classical solution, and that this solution is bounded if β < 1, whereas whenever β > 1 and 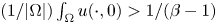$({1}/{|\Omega |})\int _\Omega u(\cdot ,0) > 1/(\beta -1)$, infinite-time blow-up occurs at least in the particular case when ρ = 0.

In order to provide an appropriate complement to this, the current study reveals that for any ρ ⩾ 0 and arbitrary β > 0, at each prescribed level γ ∈ (0, 1/(β − 1)+) one can identify an L∞-neighbourhood of the homogeneous distribution (u, v, w, z) ≡ (γ, 0, 0, 0) within which all initial data lead to globally bounded solutions that stabilize towards the constant equilibrium (u∞, 0, 0, 0) with some u∞ > 0.

Keywords

Haptotaxisboundednessstabilitycooperative parabolic system

MSC classification

Primary: 35B40: Asymptotic behavior of solutions
Secondary: 35B33: Critical exponents 35K57: Reaction-diffusion equations 35Q92: PDEs in connection with biology and other natural sciences 92C17: Cell movement (chemotaxis, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 1 , February 2022 , pp. 81 - 101
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alemany, R.. Viruses in cancer treatment. Clin. Transl. Oncol. 15 (2013), 182–188.CrossRefGoogle ScholarPubMed
Alzahrani, T., Eftimie, R. and Trucu, D.. Multiscale modelling of cancer response to oncolytic viral therapy. Math. Biosci. 310 (2019), 76–95.CrossRefGoogle ScholarPubMed
Bischoff, J. R., Kirn, D. H., Williams, A., Heise, C., Horn, S., Muna, M., Ng, L., Nye, J. A., Sampson-Johannes, A., Fattaey, A. and McCormick, F.. An adenovirus mutant that replicates selectively in p53-deficient human tumor cells. Science 274 (1996), 373–376.CrossRefGoogle ScholarPubMed
Cao, X.. Boundedness in a three-dimensional chemotaxis–haptotaxis system. Z. Angew. Math. Phys. 67 (2016), 11.CrossRefGoogle Scholar
Chen, Z.. Dampening effect of logistic source in a two-dimensional haptotaxis system with nonlinear zero-order interaction. J. Math. Anal. Appl. 492 (2020), 17 pp.CrossRefGoogle Scholar
Coffey, M. C., Strong, J. E., Forsyth, P. A. and Lee, P. W. K.. Reovirus therapy of tumors with activated Ras pathways. Science 282 (1998), 1332–1334.CrossRefGoogle Scholar
Fontelos, M. A., Friedman, A. and Hu, B.. Mathematical analysis of a model for the initiation of angiogenesis. SIAM J. Math. Anal. 33 (2002), 1330–1355.CrossRefGoogle Scholar
Friedman, A. and Tello, J. I.. Stability of solutions of chemotaxis equations in reinforced random walks. J. Math. Anal. Appl. 272 (2002), 138–163.CrossRefGoogle Scholar
Hillen, T., Painter, K. J. and Winkler, M.. Convergence of a cancer invasion model to a logistic chemotaxis model. Math. Model. Meth. Appl. Sci. 23 (2013), 165–198.CrossRefGoogle Scholar
Jain, R.. Barriers to drug delivery in solid tumors. Sci. Am. 271 (1994), 58–65.CrossRefGoogle ScholarPubMed
Komarova, N. L.. Viral reproductive strategies: how can lytic viruses be evolutionarily competitive?. J. Theor. Biol. 249 (2007), 766–784.CrossRefGoogle ScholarPubMed
Li, J. and Wang, Y.. Boundedness in a haptotactic cross-diffusion system modeling oncolytic virotherapy. J. Diff. Equ. 270 (2021), 94–113.CrossRefGoogle Scholar
Liţcanu, G. and Morales-Rodrigo, C.. Asymptotic behavior of global solutions to a model of cell invasion. Math. Models Meth. Appl. Sci. 20 (2010), 1721–1758.CrossRefGoogle Scholar
Martuza, R. L., Malick, A., Markert, J. M., Ruffner, K. L. and Coen, D. M.. Experimental therapy of human glioma by means of a genetically engineered virus mutant. Science 252 (1991), 854–856.CrossRefGoogle ScholarPubMed
Morales-Rodrigo, C. and Tello, J. I.. Global existence and asymptotic behavior of a tumor angiogenesis model with chemotaxis and haptotaxis. Math. Models Meth. Appl. Sci. 24 (2014), 427–464.CrossRefGoogle Scholar
Pang, P. Y. H. and Wang, Y.. Global boundedness of solutions to a chemotaxis–haptotaxis model with tissue remodeling. Math. Model. Meth. Appl. Sci. 28 (2018), 2211–2235.CrossRefGoogle Scholar
Porzio, M. M. and Vespri, V.. Hölder estimates for local solutions of some doubly nonlinear degenerate parabolic equations. J. Diff. Equ. 103 (1993), 146–178.CrossRefGoogle Scholar
Prüss, J., Zacher, R. and Schnaubelt, R.. Global asymptotic stability of equilibria in models for virus dynamics. Math. Model. Nat. Phenom. 3 (2008), 126–142.CrossRefGoogle Scholar
Rodriguez, N. and Winkler, M.. On the global existence and qualitative behavior of one-dimensional solutions to a model for urban crime. Preprint.Google Scholar
Russell, S. J., Peng, K.-W. and Bell, J. C.. Oncolytic virotherapy. Nat. Biotechnol. 30 (2012), 658–670.CrossRefGoogle ScholarPubMed
Stinner, C., Surulescu, C. and Winkler, M.. Global weak solutions in a PDE-ODE system modeling multiscale cancer cell invasion. SIAM J. Math. Anal. 46 (2014), 1969–2007.CrossRefGoogle Scholar
Swabb, E. A., Wei, J. and Gullino, P. M.. Diffusion and convection in normal and neoplastic tissues. Cancer Res. 34 (1974), 2814–2822.Google ScholarPubMed
Tao, X.. Global classical solutions to an oncolytic viral therapy model with triply haptotactic terms in 1D. Preprint.Google Scholar
Tao, Y. and Wang, M.. A combined chemotaxis–haptotaxis system: the role of logistic source. SIAM J. Math. Anal. 41 (2009), 1533–1558.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Energy-type estimates and global solvability in a two-dimensional chemotaxis–haptotaxis model with remodeling of non-diffusible attractant. J. Diff. Equ. 257 (2014), 784–815.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Dominance of chemotaxis in a chemotaxis–haptotaxis model. Nonlinearity 27 (2014), 1225–1239.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Large time behavior in a multidimensional chemotaxis–haptotaxis model with slow signal diffusion. SIAM J. Math. Anal. 147 (2015), 4229–4250.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Global classical solutions to a doubly haptotactic cross-diffusion system modeling oncolytic virotherapy. J. Diff. Equ. 268 (2020), 4973–4997.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. A critical virus production rate for blow-up suppression in a haptotaxis model for oncolytic virotherapy. Nonlinear Anal. 198 (2020), 17 pp.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Critical mass for infinite-time blow-up in a haptotaxis system with nonlinear zero-order interaction. Discr. Cont. Dyn. Syst. A 41 (2021), 439–454.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. A critical virus production rate for efficiency of oncolytic virotherapy. Eur. J. Appl. Math. doi: 10.1017/S0956792520000133.Google Scholar
Tao, Y. and Winkler, M.. Global smooth solutions in a two-dimensional cross-diffusion system modeling propagation of urban crime. Commun. Math. Sci., to appear.Google Scholar
Vähä-Koskela, M. and Hinkkanen, A.. Tumor restrictions to oncolytic virus. Biomedicines 2 (2014), 163–194.CrossRefGoogle ScholarPubMed
Walker, C. and Webb, G. F.. Global existence of classical solutions for a haptotaxis model. SIAM J. Math. Anal. 38 (2007), 1694–1713.CrossRefGoogle Scholar
Winkler, M.. Singular structure formation in a degenerate haptotaxis model involving myopic diffusion. J. Math. Pures Appl. 112 (2018), 118–169.CrossRefGoogle Scholar
Winkler, M. and Surulescu, C.. A global weak solutions to a strongly degenerate haptotaxis model. Commun. Math. Sci. 15 (2017), 1581–1616.CrossRefGoogle Scholar
Wong, H., Lemoine, N. and Wang, Y.. Oncolytic viruses for cancer therapy: overcoming the obstacles. Viruses 2 (2010), 78–106.CrossRefGoogle ScholarPubMed
Zhigun, A., Surulescu, C. and Uatay, A.. Global existence for a degenerate haptotaxis model of cancer invasion. Z. Angew. Math. Phys. 67 (2016), Art. 146, 29.CrossRefGoogle Scholar