No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 14 February 2012
In the system of two linear partial differential equations of the second order
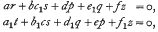
a,…,f were supposed to be polynomials in x, and a1…, f1 polynomials in y. These polynomial coefficients were subjected to certain restrictions, including conditions for the system having exactly four linearly independent solutions, and conditions for preserving the symmetrical aspect, in x and y, of the system. It has been proved that any compatible system of the contemplated form whose coefficients satisfy the stipulated conditions is equivalent with, i.e. transformable into, a hypergeometric system. More particularly it has been shown that the hypergeometric systems involved are the system of partial differential equations associated with Appell's hypergeometric function in two variables F2 and the confluent systems arising herefrom.
page 198 note * Note that accents applied to letters without suffixes denote differentiation with respect to x; accents applied to letters with suffixes denote differentiation with respect to y.
page 201 note * The excluded cases lead to trivial results.
page 205 note * The case K = K1 = o involves aa 1 – BB1C2C12=0 which is excluded. The case K = o or K1 = o may be regarded as a confluent form of the general case.
page 206 note * The details are too tedious and unimportant to reproduce; the essential point is that the left-hand member of (2.3) must be divisible by x-βy-β -x-β -y-β, which is impossible when e = E, f= Fx.