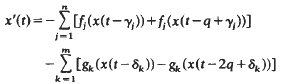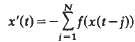Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sartori, Caterina
1982.
Asymptotic analysis of delay differential equations.
Manuscripta Mathematica,
Vol. 38,
Issue. 2,
p.
225.
Nussbaum, R. D.
1983.
Asymptotic analysis of functional differential equations and solutions of long period.
Archive for Rational Mechanics and Analysis,
Vol. 81,
Issue. 4,
p.
373.
Angelstorf, N.
and
Kirchgassner, K.
1983.
Periodic solutions of u'(t) = −f(u(t − 1)): Multiplicity results and small period solutions.
Mathematical Methods in the Applied Sciences,
Vol. 5,
Issue. 1,
p.
162.
Chow, S. -N.
Diekmann, O.
and
Mallet-Paret, J.
1985.
Stability, multiplicity and global continuation of symmetric periodic solutions of a nonlinear Volterra integral equation.
Japan Journal of Applied Mathematics,
Vol. 2,
Issue. 2,
p.
433.
Chapin, S.
and
Payne, L. E.
1985.
Asymptotic analysis of differential‐delay equations and nonuniqueness of periodic solutions.
Mathematical Methods in the Applied Sciences,
Vol. 7,
Issue. 1,
p.
223.
Nussbaum, Roger D.
1989.
Wright's equation has no solutions of period four.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 113,
Issue. 3-4,
p.
281.
Chapin, Steven A.
1989.
Periodic solutions of a differential-delay equation and the fixed point index.
Applicable Analysis,
Vol. 33,
Issue. 1-2,
p.
119.
Gopalsamy, K.
Li, Jibin
and
He, Xue-Zhong
1995.
On the construction of periodic solutions of kaplan-yorke type for some differential delay equations.
Applicable Analysis,
Vol. 59,
Issue. 1-4,
p.
65.
Weigao, Ge
1996.
Periodic solutions of the differential delay equation $$\dot x(t) = - f(x(t - 1))$$.
Acta Mathematica Sinica,
Vol. 12,
Issue. 2,
p.
113.
Ge, Weigao
1997.
Oscillatory periodic solutions of differential-delay equations with multiple lags.
Chinese Science Bulletin,
Vol. 42,
Issue. 6,
p.
444.
Li, Jibin
and
He, Xuezhong
1999.
Proof and generalization of Kaplan-Yorke’s conjecture under the condition f ' (0) > 0 on periodic solution of differential delay equations.
Science in China Series A: Mathematics,
Vol. 42,
Issue. 9,
p.
957.
Li, Jibin
Liu, Zhengrong
and
He, Xuezhong
1999.
Periodic solutions of some differential delay equations created by Hamiltonian systems.
Bulletin of the Australian Mathematical Society,
Vol. 60,
Issue. 3,
p.
377.
Nussbaum, Roger D.
2002.
Vol. 2,
Issue. ,
p.
461.
Fei, Guihua
2006.
Multiple periodic solutions of differential delay equations via Hamiltonian systems (II).
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 65,
Issue. 1,
p.
40.
Jekel, Solomon
and
Johnston, Christopher
2006.
A Hamiltonian with periodic orbits having several delays.
Journal of Differential Equations,
Vol. 222,
Issue. 2,
p.
425.
Fei, Guihua
2006.
Multiple periodic solutions of differential delay equations via Hamiltonian systems (I).
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 65,
Issue. 1,
p.
25.
Cheng, Rong
and
Xu, Junxiang
2009.
Periodic solutions for a class of non-autonomous differential delay equations.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 16,
Issue. 6,
p.
793.
Cheng, Rong
Hu, Jianhua
and
Mallet-Paret, John
2010.
Variational Approaches for the Existence of Multiple Periodic Solutions of Differential Delay Equations.
Abstract and Applied Analysis,
Vol. 2010,
Issue. 1,
Cheng, Rong
and
Zhang, Dongfeng
2010.
Existence results of periodic solutions for non-autonomous differential delay equations with asymptotically linear properties.
Nonlinear Analysis: Real World Applications,
Vol. 11,
Issue. 5,
p.
3406.
Cheng, Rong
and
Braverman, Elena
2011.
Oscillatory Periodic Solutions for Two Differential‐Difference Equations Arising in Applications.
Abstract and Applied Analysis,
Vol. 2011,
Issue. 1,