Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T17:50:20.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Parrondo's paradox for homoeomorphisms

Part of: Random dynamical systems Smooth dynamical systems: general theory

Published online by Cambridge University Press:  16 June 2021

A. Gasull Open the ORCID record for A. Gasull [Opens in a new window] ,
L. Hernández-Corbato Open the ORCID record for L. Hernández-Corbato [Opens in a new window]  and
F. R. Ruiz del Portal Open the ORCID record for F. R. Ruiz del Portal [Opens in a new window]
A. Gasull
Affiliation:
Departament de Matemàtiques, Edifici Cc, Universitat Autònoma de Barcelona, 08193 Cerdanyola del Vallès, Barcelona, Spain Centre de Recerca Matemàtica, Edifici Cc, Campus de Bellaterra, 08193 Cerdanyola del Vallès, Barcelona, Spain ([email protected])
L. Hernández-Corbato
Affiliation:
Departamento de Álgebra, Geometría y Topología Universidad Complutense de Madrid and Instituto de Ciencias Matematicas CSIC–UAM–UCM–UC3M, Madrid, Spain ([email protected])
F. R. Ruiz del Portal
Affiliation:
Departamento de Álgebra, Geometría y Topología Universidad Complutense de Madrid, 28040 Madrid, Spain ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct two planar homoeomorphisms 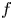$f$ and 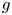$g$ for which the origin is a globally asymptotically stable fixed point whereas for 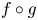$f \circ g$ and 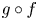$g \circ f$ the origin is a global repeller. Furthermore, the origin remains a global repeller for the iterated function system generated by 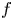$f$ and 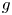$g$ where each of the maps appears with a certain probability. This planar construction is also extended to any dimension 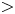$>$2 and proves for first time the appearance of the dynamical Parrondo's paradox in odd dimensions.

Keywords

Dynamical Parrondo's paradoxfixed pointslocal and global asymptotic stabilityrandom dynamical systems

MSC classification

Primary: 37C25: Fixed points, periodic points, fixed-point index theory
Secondary: 37C75: Stability theory 37H05: Foundations, general theory of cocycles, algebraic ergodic theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 4 , August 2022 , pp. 817 - 825
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ash, R. B.. Real analysis and probability. Probability and Mathematical Statistics, vol. 11. (New York-London: Academic Press, 1972).Google Scholar
Billingsley, P.. Probability and measure. Wiley Series in Probability and Mathematical Statistics. A Wiley-Interscience Publication, 3rd edition (New York: John Wiley & Sons Inc., 1995).Google Scholar
Blondel, V. D., Theys, J. and Tsitsiklis, J. N.. When is a pair of matrices stable? In Unsolved problems in mathematical systems and control theory (ed. Blondel, V. D. and Megretski, A.). (NJ: Princeton Univ. Press, 2004), 304–308.CrossRefGoogle Scholar
Cánovas, J. S., Linero, A. and Peralta-Salas, D.. Dynamic Parrondo's paradox. Physica D 218 (2006), 177–184.CrossRefGoogle Scholar
Cima, A., Gasull, A. and Mañosa, V.. Parrondo's dynamic paradox for the stability of non-hyperbolic fixed points. Discrete Contin. Dyn. Syst. 38 (2018), 889–904.CrossRefGoogle Scholar
Elaydi, S. and Sacker, R. J.. Global stability of periodic orbits of non-autonomous difference equations and population biology. J. Differ. Equ. 208 (2005), 258–273.CrossRefGoogle Scholar
Elaydi, S. and Sacker, R. J.. Periodic difference equations, population biology and the Cushing–Henson conjectures. Math. Biosci. 201 (2006), 195–207.CrossRefGoogle ScholarPubMed
Franke, J. E. and Selgrade, J. F.. Attractors for discrete periodic dynamical systems. J. Math. Anal. Appl. 286 (2003), 64–79.CrossRefGoogle Scholar
Harmer, G. P. and Abbott, D.. Losing strategies can win by Parrondo's paradox. Nature 402 (1999), 864.CrossRefGoogle Scholar
Jungers, R.. The joint spectral radius (Berlin: Spinger, 2009).CrossRefGoogle Scholar
Parrondo, J. M. R.. How to cheat a bad mathematician. in EEC HC&M Network on Complexity and Chaos (#ERBCHRX-CT940546), ISI, Torino, Italy (1996), Unpublished.Google Scholar
Selgrade, J. F. and Roberds, J. H.. On the structure of attractors for discrete, periodically forced systems with applications to population models. Physica D 158 (2001), 69–82.CrossRefGoogle Scholar
Selgrade, J. F. and Roberds, J. H.. Global attractors for a discrete selection model with periodic immigration. J. Differ. Equ. Appl. 13 (2007), 275–287.CrossRefGoogle Scholar