Article contents
On higher differentiability of solutions of parabolic systems with discontinuous coefficients and (p, q)-growth
Published online by Cambridge University Press: 26 January 2019
Abstract
We consider weak solutions 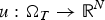 $u:\Omega _T\to {\open R}^N$ to parabolic systems of the type
$u:\Omega _T\to {\open R}^N$ to parabolic systems of the type
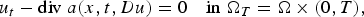 $$u_t-{\rm div}\;a(x,t,Du) = 0\quad {\rm in}\;\Omega _T = \Omega \times (0,T),$$
$$u_t-{\rm div}\;a(x,t,Du) = 0\quad {\rm in}\;\Omega _T = \Omega \times (0,T),$$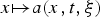 $x\mapsto a(x,t,\xi )$ under consideration may not be continuous, but may only possess a Sobolev-type regularity. In a certain sense, our assumption means that the weak derivatives
$x\mapsto a(x,t,\xi )$ under consideration may not be continuous, but may only possess a Sobolev-type regularity. In a certain sense, our assumption means that the weak derivatives 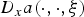 $D_xa(\cdot ,\cdot ,\xi )$ are contained in the class
$D_xa(\cdot ,\cdot ,\xi )$ are contained in the class 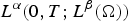 $L^\alpha (0,T;L^\beta (\Omega ))$, where the integrability exponents
$L^\alpha (0,T;L^\beta (\Omega ))$, where the integrability exponents 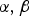 $\alpha ,\beta $ are coupled by
$\alpha ,\beta $ are coupled by
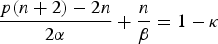 $$\displaystyle{{p(n + 2)-2n} \over {2\alpha }} + \displaystyle{n \over \beta } = 1-\kappa $$
$$\displaystyle{{p(n + 2)-2n} \over {2\alpha }} + \displaystyle{n \over \beta } = 1-\kappa $$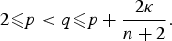 $$2 \les p < q \les p + \displaystyle{{2\kappa } \over {n + 2}}.$$
$$2 \les p < q \les p + \displaystyle{{2\kappa } \over {n + 2}}.$$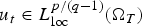 $u_t\in L^{p/(q-1)}_{{\rm loc}}(\Omega _T)$. We use the corresponding a priori estimate to deduce the existence of solutions of Cauchy–Dirichlet problems with the mentioned higher differentiability property.
$u_t\in L^{p/(q-1)}_{{\rm loc}}(\Omega _T)$. We use the corresponding a priori estimate to deduce the existence of solutions of Cauchy–Dirichlet problems with the mentioned higher differentiability property.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 1 , February 2020 , pp. 419 - 451
- Copyright
- Copyright © Royal Society of Edinburgh 2019
References
- 10
- Cited by


