Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-23T11:26:03.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple solutions for nonhomogeneous elliptic equations involving critical Sobolev exponent*

Published online by Cambridge University Press:  14 November 2011

Dao-Min Cao ,
Gong-Bao Li  and
Huan-Song Zhou
Dao-Min Cao
Affiliation:
Wuhan Institute of Mathematical Sciences, Academia Sinica, P.O. Box 71007, Wuhan 430071, P.R. China
Gong-Bao Li
Affiliation:
Wuhan Institute of Mathematical Sciences, Academia Sinica, P.O. Box 71007, Wuhan 430071, P.R. China
Huan-Song Zhou
Affiliation:
Wuhan Institute of Mathematical Sciences, Academia Sinica, P.O. Box 71007, Wuhan 430071, P.R. China
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the following problem:

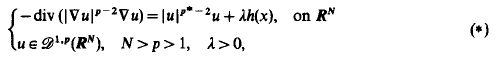
where 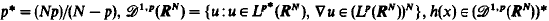is continuous on RN and h(x)≢0. By using Ekeland's variational principle and the Mountain Pass Theorem without (PS) conditions, through a careful inspection of the energy balance for the approximated solutions, we show that the probelm (*) has at least two solutions for some λ* > 0 and λ ∈ (0, λ*). In particular, if p = 2, in a different way we prove that problem (*) with λ ≡ 1 and h(x) ≧ 0 has at least two positive solutions as

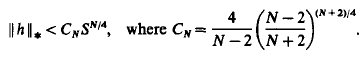
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 6 , 1994 , pp. 1177 - 1191
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ambrosetti, A. and Rabinowitz, P. H.. Dual variational methods in critical point theory and applications. J. Fund. Anal. 14 (1973), 349–381.CrossRefGoogle Scholar
2Brezis, H. and Lieb, E.. A relation between pointwise convergence of functions and convergence of functionals. Proc. Amer. Math. Soc. 88 (1983), 480–490.CrossRefGoogle Scholar
3Brezis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Comm. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
4Cao, D. M., Li, G. B. and Zhou, H. S.. The existence of two solutions to quasilinear elliptic equations on RN (Preprint).Google Scholar
5Cao, D. M. and Zhou, H. S.. Multiple positive solutions of nonhomogeneous semilinear elliptic equations in RN (Preprint).Google Scholar
6Deng, Y. B.. Existence of multiple positive solutions for - Δu + c2u = u(N + 2)/(N−2) + νf(x) in RN. Proc. Roy. Soc. Edinburgh Sect. A 122 (1992), 161–175.Google Scholar
7Graham-Eagle, J.. Monotone methods for semilinear elliptic equations in unbounded domains. J. Math. Anal. Appl. 137 (1989), 122–131.CrossRefGoogle Scholar
8Ekeland, I.. Nonconvex minimization problems. Bull. Amer. Math. Soc. 3 (1979), 443–474.CrossRefGoogle Scholar
9Li, G. B.. The existence of a weak solution of quasilinear elliptic equations with critical Sobolev exponent on unbounded domains. Acta Math. Sri. 14 (1994), 64–74.CrossRefGoogle Scholar
10Li, G. B. and Zhou, H. S.. The existence of a weak solutions of inhomogeneous quasilinear elliptic equations with critical growth conditions. To appear in Acta Math. Sinica, New Series.Google Scholar
11Talenti, G.. Best constant in Sobolev inequality. Ann. Mat. Pure Appl. 110 (1976), 353–372.CrossRefGoogle Scholar
12Tarantello, G.. On nonhomogeneous elliptic equations involving critical Sobolev exponent. Ann. Inst. H. Poincare Anal. Non Lineaire 9 (1992), 243–261.CrossRefGoogle Scholar
13Zhu, X. P.. Nontrivial solution of quasilinear elliptic equations involving critical Sobolev exponents. Scientia Sinica A 31 (1988), 1161–1181.Google Scholar