Article contents
Multiparameter Sturm theory
Published online by Cambridge University Press: 14 November 2011
Extract
Let Sturm–Liouville problems
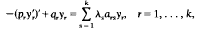
with continuous coefficients and appropriate boundary conditions, be coupled by the eigenvalue λ = (λ1, … λk). When k = 1, there are various oscillation, perturbation and comparison theorems concerning existence and continuous or monotonic dependence of eigenvalues, eigenfunctions and their zeros (i.e. focal points).
We attempt a unified theory for such results, valid for general fc, under conditions known as "left" and “right” definiteness. A representative result may be stated loosely as follows: if LD holds then (elementwise) monotonic dependence of p, q and the matrix [ars] forces monotonic dependence of λ. LD is a generalisation of the “polar” case for k = 1, and was originally conceived for a quite different purpose, viz. completeness of eigenfunctions via elliptic partial differential equation theory.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 99 , Issue 1-2 , 1984 , pp. 173 - 184
- Copyright
- Copyright © Royal Society of Edinburgh 1984
References
- 9
- Cited by


