No CrossRef data available.
Published online by Cambridge University Press: 19 September 2022
Let $G$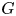 be a compact connected simple Lie group of type $(n_{1},\,\ldots,\,n_{l})$
be a compact connected simple Lie group of type $(n_{1},\,\ldots,\,n_{l})$ , where $n_{1}<\cdots < n_{l}$
, where $n_{1}<\cdots < n_{l}$ . Let $\mathcal {G}_k$
. Let $\mathcal {G}_k$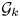 be the gauge group of the principal $G$
be the gauge group of the principal $G$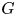 -bundle over $S^{4}$
-bundle over $S^{4}$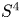 corresponding to $k\in \pi _3(G)\cong \mathbb {Z}$
corresponding to $k\in \pi _3(G)\cong \mathbb {Z}$ . We calculate the mod-$p$
. We calculate the mod-$p$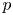 homology of the classifying space $B\mathcal {G}_k$
homology of the classifying space $B\mathcal {G}_k$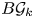 provided that $n_{l}< p-1$
provided that $n_{l}< p-1$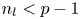 .
.