Article contents
Fatou components and singularities of meromorphic functions
Published online by Cambridge University Press: 23 January 2019
Abstract
We prove several results concerning the relative position of points in the postsingular set P(f) of a meromorphic map f and the boundary of a Baker domain or the successive iterates of a wandering component. For Baker domains we answer a question of Mihaljević-Brandt and Rempe-Gillen. For wandering domains we show that if the iterates Un of such a domain have uniformly bounded diameter, then there exists a sequence of postsingular values pn such that 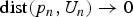 ${\rm dist} (p_n, U_n)\to 0$ as
${\rm dist} (p_n, U_n)\to 0$ as  $n\to \infty $. We also prove that if
$n\to \infty $. We also prove that if 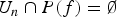 $U_n \cap P(f)=\emptyset $ and the postsingular set of f lies at a positive distance from the Julia set (in ℂ), then the sequence of iterates of any wandering domain must contain arbitrarily large disks. This allows to exclude the existence of wandering domains for some meromorphic maps with infinitely many poles and unbounded set of singular values.
$U_n \cap P(f)=\emptyset $ and the postsingular set of f lies at a positive distance from the Julia set (in ℂ), then the sequence of iterates of any wandering domain must contain arbitrarily large disks. This allows to exclude the existence of wandering domains for some meromorphic maps with infinitely many poles and unbounded set of singular values.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 633 - 654
- Copyright
- Copyright © Royal Society of Edinburgh 2019
References
- 13
- Cited by


