Article contents
2-dimensional Coxeter groups are biautomatic
Published online by Cambridge University Press: 23 March 2021
Abstract
Let W be a 2-dimensional Coxeter group, that is, one with 1/mst + 1/msr + 1/mtr ≤ 1 for all triples of distinct s, t, r ∈ S. We prove that W is biautomatic. We do it by showing that a natural geodesic language is regular (for arbitrary W), and satisfies the fellow traveller property. As a consequence, by the work of Jacek Świątkowski, groups acting properly and cocompactly on buildings of type W are also biautomatic. We also show that the fellow traveller property for the natural language fails for 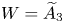 $W=\widetilde {A}_3$.
$W=\widetilde {A}_3$.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 2 , April 2022 , pp. 382 - 401
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
Footnotes
Partially supported by NSERC and AMS.
Partially supported by (Polish) Narodowe Centrum Nauki, UMO-2018/30/M/ST1/00668.
References
- 1
- Cited by



