Research Article
Locally bounded spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 321-325
-
- Article
-
- You have access
- Export citation
Automorphisms of transformation semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 327-329
-
- Article
-
- You have access
- Export citation
Outer automorphisms of ordered permutation groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 331-344
-
- Article
-
- You have access
- Export citation
Near-rings of quotients of endomorphism near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 345-352
-
- Article
-
- You have access
- Export citation
Some algebraic properties of F(X) and K(X)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 353-361
-
- Article
-
- You have access
- Export citation
On rearranging maximal functions in Rn
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 363-369
-
- Article
-
- You have access
- Export citation
On a result of M. Heins
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 371-373
-
- Article
-
- You have access
- Export citation
Extensions relative to a Serre class
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 375-381
-
- Article
-
- You have access
- Export citation
Topological aspects of suitable theories
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 383-391
-
- Article
-
- You have access
- Export citation
A result on the convolution of distributions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 393-395
-
- Article
-
- You have access
- Export citation
Book Reviews
D. H. Fremlin, Topological Riesz Spaces and Measure Theory (Cambridge, 1974), xiv+266 pp., £5·90.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 397
-
- Article
-
- You have access
- Export citation
P. L. Walker, An Introduction to Complex Analysis(Adam Hilger, London, 1974), viii+141 pp., £4·50.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 397-399
-
- Article
-
- You have access
- Export citation
F. W. Anderson and K. R. Fuller, Rings and Categories of Modules (Graduate Texts in Mathematics, vol. 13, Springer-Verlag, 1974), ix + 339 pp., DM.36.30, $14.80.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 399
-
- Article
-
- You have access
- Export citation
S. K. Berberian, Lectures in Functional Analysis and Operator Theory (Graduate Texts in Mathematics Vol. 15, Springer-Verlag, 1974), ix+345 pp., DM38.50, $15.70.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 399-400
-
- Article
-
- You have access
- Export citation
A. J. Weir, General Integration and Measure (Cambridge University Press, 1974), xi+298 pp., £5·70.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 400
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 19 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 19 issue 4 Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b6
-
- Article
-
- You have access
- Export citation

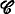 be a category with finite products and a final object and let
be a category with finite products and a final object and let 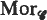 (
( denotes the Lebesgue measure of the set specified. We shall suppose that λ(
denotes the Lebesgue measure of the set specified. We shall suppose that λ(
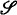 of modules with the property that
of modules with the property that 

