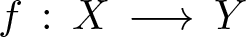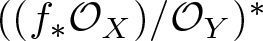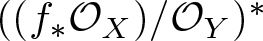Pushforward of structure sheaf and virtual global generation

Abstract

Let $f\,:\,X\,\longrightarrow \,Y$ be a generically smooth morphism between irreducible smooth projective curves over an algebraically closed field of arbitrary characteristic. We prove that the vector bundle $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated. Moreover, $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample if and only if f is genuinely ramified.

1. Introduction

Let X and Y be irreducible smooth projective curves over an algebraically closed field k – there is no assumption on the characteristic of k – and let $f\,:\,X\,\longrightarrow \,Y$ be a generically smooth morphism. Then, we have ${\mathcal O}_Y\, \subset\, f_*{\mathcal O}_X$. In [4] it was shown that the homomorphism of étale fundamental groups $f_*\, :\, \pi^{\rm et}_1(X)\, \longrightarrow\,\pi^{\rm et}_1(Y)$ induced by f is surjective if and only if ${\mathcal O}_Y$ is the unique maximal semistable subsheaf of $f_*{\mathcal O}_X$. We call f to be genuinely ramified if ${\mathcal O}_Y$ is the unique maximal semistable subsheaf of $f_*{\mathcal O}_X$. On the other hand, f is called primitive if the above homomorphism $f_*$ of étale fundamental groups is surjective [5]. So f is genuinely ramified if and only if it is primitive.

The main result of [4] says the following: If $f\,:\,X\,\longrightarrow \,Y$ is genuinely ramified, and E is a stable vector bundle on Y, then $f^*E$ is also stable. This was proved by investigating the quotient bundle $(f_*{\mathcal O}_X)/{\mathcal O}_Y$.

The dual vector bundle $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is called the Tschirnhausen bundle for f (see [5]). The following is the main result of [5]: Let $f\,:\,X\,\longrightarrow \,Y$ be a general primitive degree r cover, where ${\rm genus}(X)\,=\, g$ and ${\rm genus}(Y)\,=\, h$, over an algebraically closed field of characteristic zero or greater than r. Then

1. (1) $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is semistable if $h\,=\, 1$, and

2. (2) $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is stable if $h \,\geq \, 2$.

Note that the above mentioned result of [4] can be reformulated as follows: Let $f\,:\,X\,\longrightarrow \,Y$ be a generically smooth morphism between irreducible smooth projective curves. Then $f^*E$ is stable for every stable vector bundle E on Y if and only if:

\begin{equation*} \mu_{\rm min}(((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*) \, \gt \, 0. \end{equation*}

(Recall that µ _min denotes the slope of the smallest quotient [9, p. 16, Definition 1.3.2].) See [5] for more on Tschirnhausen bundles.

A vector bundle on an irreducible smooth projective curve Z is called virtually globally generated if its pullback, under some surjective morphism to Z from some irreducible smooth projective curve, is generated by its global sections; see $\S$ 3.

We prove the following (see Theorem 3.3):

Let X and Y be irreducible smooth projective curves and:

\begin{equation*} f\, :\, X\, \longrightarrow\, Y, \end{equation*}

a generically smooth morphism. Then $(f_*{\mathcal O}_X)^*$ is virtually globally generated.

Note that this implies that: $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated (see Corollary 3.5).

In Remark 3.6 it is shown that Corollary 3.5 fails in higher dimensions.

We prove the following (see Corollary 3.2):

Let $f\, :\, X\, \longrightarrow\, Y$ be a generically smooth morphism between two irreducible smooth projective curves. Then f is genuinely ramified if and only if $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample.

It may be mentioned that the condition in Theorem 3.3 and Corollary 3.2 that f is generically smooth is essential. To give an example, take Y to be a smooth projective curve of genus at least two, and let $F_Y\, :\, Y\, \longrightarrow\, Y,$ be the absolute Frobenius morphism of Y. Then $(F_{Y*}{\mathcal O}_Y))/{\mathcal O}_Y$ is in fact ample.

2. Genuinely ramified maps, direct image and ampleness

The base field k is assumed to be algebraically closed. For a vector bundle E on an irreducible smooth projective curve X, if

\begin{equation*} E_1\, \subset\, \cdots\, \subset\, E_{n-1}\, \subset\, E_n\,=\, E, \end{equation*}

is the Harder–Narasimhan filtration of E, then define $\mu_{\rm max}(E)\,:=\, \mu(E_1)$ and $\mu_{\rm min}(E)\, =\, \mu(E/E_{n-1})$ [9]. The subbundle $E_1\, \subseteq\, E$ is called the maximal semistable subsheaf of E.

Let X and Y be irreducible smooth projective curves and

(2.1)\begin{equation} f\, :\, X\, \longrightarrow\, Y, \end{equation}

a dominant generically smooth morphism. It is straight-forward to check that:

(2.2)\begin{equation} \mu_{\rm max}(f_*{\mathcal O}_X)\, =\, 0. \end{equation}

Indeed, $\mu_{\rm max}(f_* {\mathcal O}_X)\, \leq\, 0$ because $\text{degree}({\mathcal O}_X)\,=\, 0$ [4, p. 12824, Lemma 2.2]. On the other hand, we have ${\mathcal O}_Y\, \subset\, f_*{\mathcal O}_X$, which implies that $\mu_{\rm max}(f_*{\mathcal O}_X)\, \geq\, 0$, and thus (2.2) holds.

The following proposition was proved in [4].

Proposition 2.1. ([4, p. 12828, Proposition 2.6] and [4, p. 12830, Lemma 3.1])

The following five statements are equivalent:

1. (1) The maximal semistable subsheaf of $f_*{\mathcal O}_X$ is ${\mathcal O}_Y$.

2. (2) $\dim H^0(X,\, f^*f_* {\mathcal O}_X)\,=\, 1$.

3. (3) The fibre product $X\times_Y X$ is connected.

4. (4) The homomorphism of étale fundamental groups $f_*\, :\, \pi^{\rm et}_1(X)\, \longrightarrow\,\pi^{\rm et}_1(Y)$ induced by f is surjective.

5. (5) The map f does not factor through any nontrivial finite étale covering of Y.

Any morphism f as in (2.1) is called genuinely ramified if the (equivalent) statements in Proposition 2.1 hold [4, p. 12828, Definition 2.5].

Proposition 2.2. Let $f\, :\, X\, \longrightarrow\, Y$ be a genuinely ramified morphism of smooth projective curves. Then the vector bundle $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample.

Proof. Since f is genuinely ramified, from Proposition 2.1 it follows that:

\begin{equation*}\mu_{\rm max}((f_*{\mathcal O}_X)/{\mathcal O}_Y)\, \lt \, 0,\end{equation*}

and hence we have:

(2.3)\begin{equation} \mu_{\rm min}(((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*)\,=\, - \mu_{\rm max}((f_*{\mathcal O}_X)/{\mathcal O}_Y)\, \gt \, 0. \end{equation}

When the characteristic of k is zero, a vector bundle W on Y is ample if and only if the degree of every nonzero quotient of W is positive [7, p. 84, Theorem 2.4]. Therefore, from (2.3) we conclude that: $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample, when the characteristic of k is zero. However, this characterization of ample bundles fails when the characteristic of k is positive (see [7, Section 3] for such examples).

We will inductive construct a sequence of vector bundles $\{V_i\}_{i \geq 0}$ on Y. First set $V_0\, =\, {\mathcal O}_Y$. For any $i\,\geq\,1$, let $V_i\,=\, f_*f^*V_{i-1}$. Since we have

\begin{equation*}{\mathcal O}_Y\, \subset\, V_1\,=\, f_*f^*{\mathcal O}_Y\,=\, f_*{\mathcal O}_X,\end{equation*}

it can be deduced that:

(2.4)\begin{equation} {\mathcal O}_Y\, \subset\, V_i, \end{equation}

for all $i\, \geq\, 0$. Indeed, this follows inductively, as the inclusion map ${\mathcal O}_Y\, \hookrightarrow\, V_j$ produces:

\begin{equation*} {\mathcal O}_Y \, \subset\, f_*{\mathcal O}_X \,=\, f_* f^*{\mathcal O}_Y \, \hookrightarrow\, f^*f_*V_j\,=\, V_{j+1}. \end{equation*}

This proves (2.4) inductively.

Next we will show that the subsheaf ${\mathcal O}_Y$ in (2.4) is the maximal semistable subsheaf of V_i. This will also be proved using an inductive argument.

First, ${\mathcal O}_Y$ is obviously the maximal semistable subsheaf of V ₀. Next, from Proposition 2.1 we know that ${\mathcal O}_Y$ is the maximal semistable subsheaf of V ₁ (recall that f is genuinely ramified). Let

\begin{equation*} {\mathcal O}_Y \,=\, E^1_1\, \subset\, E^1_2\, \subset\, \cdots\, \subset\, E^1_{n_1-1}\, \subset\, E^1_{n_1}\,=\, V_1, \end{equation*}

be the Harder–Narasimhan filtration of V ₁. Since $f^*W$ is semistable if W is so (see [4, pp. 12823–12824, Remark 2.1]), we conclude that:

(2.5)\begin{equation} {\mathcal O}_X \,=\, f^*E^1_1\, \subset\, \cdots\, \subset\, f^*E^1_{n_1-1}\, \subset\, f^*E^1_{n_1}\,=\, f^*V_1, \end{equation}

is the Harder–Narasimhan filtration of $f^*V_1$.

For any vector bundle B on X, we have $\mu_{\rm max}(f_* B) \, \leq\, \mu_{\rm max}(B)/\text{degree}(f)$ [4, Lemma 2.2, p. 12824]. In view of the Harder–Narasimhan filtration in (2.5), this implies that:

\begin{equation*} \mu_{\rm max}((f_*f^*E^1_{j+1})/(f_*f^*E^1_{j})) \, \lt \, 0, \end{equation*}

for all $1\,\leq\, j\, \, \leq\, n_1-1$, because $\mu_{\rm max}((f^*E^1_{j+1})/(f^*E^1_{j})) \, \lt \, 0$. Also, as noted before, the maximal semistable subsheaf of $f_*{\mathcal O}_X$ is ${\mathcal O}_Y$. Combining these we conclude that ${\mathcal O}_Y$ is the maximal semistable subsheaf of $f_*f^*V_1\,=\, V_2$.

The above argument works inductively. To explain this, let

\begin{equation*} {\mathcal O}_Y \,=\, E^\ell_1\, \subset\, E^\ell_2\, \subset\, \cdots\, \subset\, E^\ell_{n_\ell-1}\, \subset\, E^\ell_{n_\ell} \,=\, V_\ell, \end{equation*}

be the Harder–Narasimhan filtration of $V_\ell$. As before, we have:

\begin{equation*} \mu_{\rm max}((f_*f^*E^\ell_{j+1})/(f_*f^*E^\ell_{j})) \, \lt \, 0, \end{equation*}

for all $1\,\leq\, j\, \, \leq\, n_\ell-1$, because $\mu_{\rm max}((f^*E^\ell_{j+1})/(f^*E^\ell_{j})) \, \lt \, 0$. Using this together with the fact that the maximal semistable subsheaf of $f_*{\mathcal O}_X$ is ${\mathcal O}_Y$ we conclude that ${\mathcal O}_Y$ is the maximal semistable subsheaf of $f_*f^*V_\ell\,=\, V_{\ell+1}$.

The projection formula (see [8, p. 124, Ch. II, Ex. 5.1(d)], [11]) gives that $V_{i+1} \,=\, f_*f^*V_i\,=\, V_i\otimes (f_*{\mathcal O}_X)$ for all $i\, \geq\, 1$. This implies that:

(2.6)\begin{equation} V_i\,=\, (f_*{\mathcal O}_X)^{\otimes i}\,=\, V^{\otimes i}_1, \end{equation}

for all $i\, \geq\, 1$.

Now we assume that the characteristic of k is positive (recall that the proposition was proved when the characteristic of k is zero). Let p be the characteristic of k. Let

\begin{equation*}F_Y\, :\, Y\, \longrightarrow\, Y\end{equation*}

be the absolute Frobenius morphism of Y. For any vector bundle W on Y, we have the inclusion:

\begin{equation*} F^*_Y W\, \subset\, W^{\otimes p}, \end{equation*}

it is constructed using the map $W\, \longrightarrow\, W^{\otimes p}$ defined by $v\, \longmapsto\, v^{\otimes p}$. Therefore, from (2.6) we have

(2.7)\begin{equation} (F^n_Y)^* V_1\, \subset\, (V_1)^{\otimes np}\,=\, V_{np} \end{equation}

for all $n\, \geq\, 1$. Since ${\mathcal O}_Y$ in (2.4) is the maximal semistable subsheaf of V_i, from (2.7) we have:

\begin{equation*} (F^n_Y)^* (V_1/{\mathcal O}_Y)\,=\, ((F^n_Y)^* V_1)/{\mathcal O}_Y \, \subset\, V_{np}/{\mathcal O}_Y, \end{equation*}

and

(2.8)\begin{equation} \mu_{\rm max}((F^n_Y)^* (V_1/{\mathcal O}_Y)) \, \lt \, 0, \end{equation}

because $\mu_{\rm max}(V_{np}/{\mathcal O}_Y) \, \lt \, 0$.

From (2.8) it follows that:

\begin{equation*} \mu_{\rm min}((F^n_Y)^* (V_1/{\mathcal O}_Y)^*) \,=\, - \mu_{\rm max}((F^n_Y)^* (V_1/{\mathcal O}_Y)) \, \gt \, 0, \end{equation*}

for all $n\, \geq\, 1$. This implies that $(V_1/{\mathcal O}_Y)^*\,=\, ((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample [1, p. 542, Theorem 2.2].

3. Virtual global generation

Let E be a vector bundle on an irreducible smooth projective curve Z. It will be called virtually globally generated if there is a finite surjective morphism:

\begin{equation*} \phi\, :\,M\, \longrightarrow\, Z, \end{equation*}

from an irreducible smooth projective curve M such that $\phi^*E$ is generated by its global sections. The vector bundle E is called étale trivializable if there is a pair $(M,\, \phi)$ as above such that ϕ is étale and $\phi^*E$ is trivializable.

If $\text{degree}(E)\, \lt \, 0$, then E is not virtually globally generated. More generally, E is not virtually globally generated if it admits a quotient of negative degree. To give a nontrivial example of vector bundle which is not virtually globally generated, let Z be a compact connected Riemann surface of genus g, with $g\, \geq\, 2$. Note that the free group of g generators is a quotient of $\pi_1(Z)$. To see this, express $\pi_1(Z)$ as the quotient of the free group, with generators $a_1,\, \cdots,\, a_g,\, b_1,\, \cdots,\, b_g$, by the single relation $\prod_{i=1}^g [a_i,\, b_i]\,=\, 1$. Then the quotient of $\pi_1(Z)$ by the normal subgroup generated by $b_1,\, \cdots,\, b_g$ is the free group generated by $a_1,\, \cdots,\, a_g$. Therefore, there is homomorphism:

\begin{equation*} \rho\, \, :\,\, \pi_1(Z)\,\, \longrightarrow\,\, \text{U}(r), \end{equation*}

where $\text{U}(r)$ is the group of r × r unitary matrices, such that $\rho(\pi_1(Z))$ is a dense subgroup of $\text{U}(r)$ (the subgroup of $\text{U}(r)$ generated by two general elements of it is dense in ${\rm U}(r)$). Let E denote the flat unitary vector bundle on Z given by ρ. This vector bundle E is stable of degree zero [10]. Let M be a compact connected Riemann surface and

\begin{equation*} \phi\, :\,M\, \longrightarrow\, Z, \end{equation*}

a surjective holomorphic map. Since the image of the induced homomorphism:

\begin{equation*} \phi_*\,\, :\,\,\pi_1(M)\,\, \longrightarrow\,\, \pi_1(Z), \end{equation*}

is a subgroup of $\pi_1(Z)$ of finite index, the image of the following composition of homomorphisms:

\begin{equation*} \pi_1(M)\, \,\stackrel{\phi_*}{\longrightarrow}\, \,\pi_1(Z) \,\, \stackrel{\rho}{\longrightarrow}\,\, \text{U}(r), \end{equation*}

is a dense subgroup of $\text{U}(r)$. This implies that $\phi^*E$ is a stable vector bundle of degree zero [10]. In particular, we have

\begin{equation*} H^0(M,\, \phi^*E)\,=\, 0. \end{equation*}

Hence E is not virtually globally generated.

Theorem 3.1. Let X and Y be irreducible smooth projective curves over k and

\begin{equation*} f\, :\, X\, \longrightarrow\, Y, \end{equation*}

a generically smooth morphism. Then $f_*{\mathcal O}_X$ fits in a short exact sequence of vector bundles on Y:

\begin{equation*} 0\, \longrightarrow\, E \, \longrightarrow\, f_*{\mathcal O}_X \, \longrightarrow\, V \, \longrightarrow\, 0, \end{equation*}

where E is étale trivializable and $V^*$ is ample.

Proof. Let

(3.1)\begin{equation} S^f\, \subset\,f_*{\mathcal O}_X, \end{equation}

be the maximal semistable subbundle. From (2.2) we know that $\text{degree}(S^f)\,=\, 0$.

The algebra structure of ${\mathcal O}_X$ produces an algebra structure on the direct image $f_*{\mathcal O}_X$. The subsheaf S^f in (3.1) is a subalgebra. Moreover, there is an étale covering $g\, :\, Z\, \longrightarrow\, Y$ such that:

• • f factors through g, meaning there is a morphism:

  (3.2)\begin{equation} h\, :\, X\, \longrightarrow\, Z \end{equation}

  such that $g\circ h\,=\, f$, and

• • the subsheaf $g_*{\mathcal O}_Z \, \subset\,f_*{\mathcal O}_X$ coincides with S^f.

(See the proof of [4, p. 12828, Proposition 2.6] and [4, p. 12829, (2.13)].) Moreover, the map h in (3.2) is genuinely ramified [4, p. 12829, Corollary 2.7].

Consider the short exact sequence of vector bundles on Y:

(3.3)\begin{equation} 0\, \longrightarrow\, S^f \, \longrightarrow\, f_*{\mathcal O}_X \, \longrightarrow\, Q\,:=\,(f_*{\mathcal O}_X)/S^f \, \longrightarrow\, 0. \end{equation}

The pullback $g^*Q$, where Q is the vector bundle in (3.3), is identified with $(h_*{\mathcal O}_X)/{\mathcal O}_Z$, where h is the map in (3.2). From Proposition 2.2 we know that $((h_*{\mathcal O}_X)/{\mathcal O}_Z)^*$ is ample, Since $((h_*{\mathcal O}_X)/{\mathcal O}_Z)^*\,=\, g^*Q^*$, this implies that $Q^*$ in (3.3) is ample (see [6, p. 73, Proposition 4.3]).

Since $Q^*$ is ample, in view of (3.3), it suffices to prove that S^f is a finite vector bundle.

Fix an étale Galois covering $\varphi\, :\, M\, \longrightarrow\, Y$ that dominates g. In other words, there is a morphism:

\begin{equation*} \beta \, :\, M\, \longrightarrow\, Z \end{equation*}

such that $g\circ\beta\,=\, \varphi$. Since φ is an étale Galois covering, the vector bundle $\varphi^*\varphi_* {\mathcal O}_M$ is trivializable. On the other hand,

\begin{equation*} S^f\,=\, g_*{\mathcal O}_Z\, \subset\, \varphi_*{\mathcal O}_M, \end{equation*}

and S^f is a subbundle of $\varphi_*{\mathcal O}_M$. Consider the subbundle

(3.4)\begin{equation} \varphi^*S^f\, \subset\, \varphi^*\varphi_* {\mathcal O}_M. \end{equation}

We have $\text{degree}(\varphi^*S^f)\,=\, 0$, because $\text{degree}(S^f)\,=\, 0$, and we also know that $\varphi^*\varphi_* {\mathcal O}_M$ is trivializable. Consequently, the subbundle $\varphi^*S^f$ in (3.4) is also trivializable. Hence S^f is étale trivializable.

Corollary 3.2. Let $f\, :\, X\, \longrightarrow\, Y$ be a generically smooth morphism between two irreducible smooth projective curves. Then f is genuinely ramified if and only if $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample.

Proof. In view of Proposition 2.2 it suffices to show that $((f_*{\mathcal O}_X)/ {\mathcal O}_Y)^*$ is not ample if f is not genuinely ramified. If f is not genuinely ramified, then $\text{rank}(S^f)\, \geq\, 2$ (see (3.1)). Hence $(S^f/{\mathcal O}_Y)^*$ is a quotient of $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ (see (3.3)). But $\text{degree}((S^f/{\mathcal O}_Y)^*)\,=\, 0$ because $\text{degree}((S^f)\,=\, 0$. Now $((f_*{\mathcal O}_X)/ {\mathcal O}_Y)^*$ is not ample because its quotient $(S^f/{\mathcal O}_Y)^*$ is not ample.

Theorem 3.3. Let X and Y be irreducible smooth projective curves and

\begin{equation*} f\, :\, X\, \longrightarrow\, Y, \end{equation*}

a generically smooth morphism. Then $(f_*{\mathcal O}_X)^*$ is virtually globally generated.

Proof. First assume that the characteristic of k is zero. We will show that the short exact sequence in (3.3) splits. First, the inclusion map ${\mathcal O}_Z \, \hookrightarrow\, h_*{\mathcal O}_X$ splits naturally, where h is the map in (3.2); in other words,

\begin{equation*} h_*{\mathcal O}_X\,=\, {\mathcal O}_Z\oplus F\, ; \end{equation*}

the fibre of F over any $z\, \in\, Z$ is the space of functions on $h^{-1}(z)$ whose sum is zero. Now we have

(3.5)\begin{equation} f_*{\mathcal O}_X\,=\, g_*h_*{\mathcal O}_X\,=\, g_*({\mathcal O}_Z\oplus F)\,=\, (g_*{\mathcal O}_Z)\oplus g_* F\,=\, S^f\oplus g_*F. \end{equation}

From (3.3) and (3.5) it follows that the vector bundle $g_*F$ is isomorphic to Q. Therefore, from (3.5) we have

(3.6)\begin{equation} (f_*{\mathcal O}_X)^*\,=\, (S^f)^*\oplus Q^*. \end{equation}

Now $(S^f)^*$ is virtually globally generated because S^f is étale trivializable, and $Q^*$ is virtually globally generated because $Q^*$ is ample by Theorem 3.1 (see [3, p. 46, Theorem 3.6]). Therefore, from (3.6) it follows that $(f_*{\mathcal O}_X)^*$ is virtually globally generated.

Next assume that the characteristic of k is positive. As before,

\begin{equation*}F_Y\, :\, Y\, \longrightarrow\, Y\end{equation*}

is the absolute Frobenius morphism of Y. Consider the exact sequence in (3.3); recall that S^f is the maximal semistable subsheaf of $f_*{\mathcal O}_X$. Therefore, there is an integer n ₀ such that for all $n\, \geq\, n_0$, we have

\begin{equation*} (F^n_Y)^*f_*{\mathcal O}_X\,=\, (F^n_Y)^* S^f\oplus (F^n_Y)^* Q \end{equation*}

[2, p. 356, Proposition 2.1]. Therefore,

(3.7)\begin{equation} (F^n_Y)^*(f_*{\mathcal O}_X)^*\,=\, (F^n_Y)^* (S^f)^*\oplus (F^n_Y)^* Q^*. \end{equation}

Now $(F^n_Y)^* (S^f)^*$ is virtually globally generated because S^f is étale trivializable and the Frobenius morphism commutes with étale morphisms. Also, $Q^*$ is virtually globally generated because $Q^*$ is ample by Theorem 3.1 (see [2, p. 357, Theorem 2.2]). Therefore, from (3.7) it follows that $(f_*{\mathcal O}_X)^*$ is virtually globally generated.

Corollary 3.4. Let X and Y be irreducible smooth projective curves and

\begin{equation*} f\, :\, X\, \longrightarrow\, Y, \end{equation*}

a generically smooth morphism. Then the following statements hold:

• • If the characteristic of k is zero, then

  \begin{equation*} (f_*{\mathcal O}_X)^*\,=\, E\oplus A, \end{equation*}

  where E is étale trivializable and A is ample.

• • If the characteristic of k is positive, then there is an integer n such that:

  \begin{equation*} (F^n_Y)^*(f_*{\mathcal O}_X)^*\,=\, E\oplus A, \end{equation*}

  where E is étale trivializable and A is ample.

Proof. In view of Theorem 3.3, this follows immediately from [3, p. 40, Theorem 1.1].

Corollary 3.5. Let X and Y be irreducible smooth projective curves and

\begin{equation*} f\, :\, X\, \longrightarrow\, Y, \end{equation*}

a generically smooth morphism. Then $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated.

Proof. From Theorem 3.3 we know that there is a finite surjective map:

\begin{equation*} \phi\, :\,M\, \longrightarrow\, Y, \end{equation*}

such that $\phi^*(f_*{\mathcal O}_X)^*$ is generated by its global sections. We have the short exact sequence of vector bundles on M:

(3.8)\begin{equation} 0\, \longrightarrow\, \phi^*((f_*{\mathcal O}_X)/{\mathcal O}_Y)^* \, \longrightarrow\, \phi^*(f_*{\mathcal O}_X)^* \, \longrightarrow\, \phi^*({\mathcal O}_Y)^*\,=\, {\mathcal O}_M \, \longrightarrow\, 0. \end{equation}

Since $\phi^*(f_*{\mathcal O}_X)^*$ is generated by its global sections, it has a section that projects to a nonzero section of ${\mathcal O}_M$. Choosing such a section we obtain a splitting of (3.8). Since $\phi^*(f_*{\mathcal O}_X)^*$ is generated by its global sections, its direct summand $\phi^*((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is also generated by its global sections.

Remark 3.6. Corollary 3.5 is not valid in higher dimensions. To give an example, let X denote ${\mathbb C}{\mathbb P}^2$ blown up at the point $(1,\, 0,\, 0)$. The involution of ${\mathbb C}{\mathbb P}^2$ defined by $(x,\, y,\, z)\, \longmapsto\, (x,\,-y,\, -z)$ lifts to X; let

\begin{equation*} \tau\, :\, X\, \longrightarrow\, X, \end{equation*}

be this lifted involution. Set $Y\,:=\, X/({\mathbb Z}/2{\mathbb Z})$ to be the quotient of X for the action of ${\mathbb Z}/2{\mathbb Z}$ given by τ. Let

\begin{equation*} f\, :\, X\, \longrightarrow\, X/({\mathbb Z}/2{\mathbb Z})\,=\, Y, \end{equation*}

be the quotient map. Then the line bundle $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is not virtually globally generated. To see this, first note that the line bundle $f^*(((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*)$ is virtually globally generated if $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated. But

\begin{equation*}f^*(((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*)\, =\, {\mathcal O}_{X}(D_e+D_\infty),\end{equation*}

where $D_e\, \subset\, X$ is the exceptional divisor and $D_\infty\, \subset\, X$ is the inverse image of

\begin{equation*} \{(0,\, y,\, z)\,\in\, {\mathbb C}{\mathbb P}^2\,\, \mid\,\, y,\, z\, \in\, {\mathbb C}\}\, \subset\, {\mathbb C}{\mathbb P}^2. \end{equation*}

It is easy to see that ${\mathcal O}_{X}(D_e+D_\infty)$ is not virtually globally generated. Indeed, if

\begin{equation*}\varpi\, :\, Z\, \longrightarrow\, X\end{equation*}

is a finite surjective proper map, then every section of $\varpi^*{\mathcal O}_{X}(D_e+D_\infty)$ vanishes on $\varpi^{-1}(D_e)$.