No CrossRef data available.
Article contents
On the Relation between Inverse Factorial Series and Binomial Coefficient Series*
Published online by Cambridge University Press: 20 January 2009
Extract
The chief aim of this note is to investigate directly the relation between the inverse factorial series
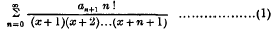
and the binomial coefficient series, or Newton's interpolation formula,
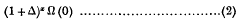
which may also represent Ω(x), the sum of the series (1).
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1924
Footnotes
Added August 10th, 1925.—Science Progress for July 1925 notes a paper by J. Horn, “Math. Zeitschrift” 21 (1924) 85.95, in whioh work on differential and difference equations, previously done with inverse factorial series, is carried out with binomial coefficient series. I have been unable to consult the paper itself to see what points in the connection between the two types of series are exemplified.
References
† Further references to this paper will be given as Norlünd (1923).
* Acta Math. 37 (1914) 344. Further references to this are given as Norlünd (1914).
* Norlünd (1914), Theorem VII, 361.
† Norlünd (1923), 43.
* Pinchbrle, , Annales Sci. de l'Ecole Normale (3), 22 (1905), 50.Google Scholar
Bromwich, , loc. cit., p. 254, Ex. 1.Google Scholar
* By the test given by Hardy, . Proc. Lond. Math. Soc. (2), 4 (1907), 250–1.Google Scholar
† Whittaker, E. T., Proc. Royal Soc. Edinburgh, XXXV., (1915), 181–194.CrossRefGoogle Scholar


